Моделирование прохождения электромагнитной волны через антиотражающую алмазную структуру

Достижения в области газофазного синтеза позволяют получать поликристалличес-кие алмазные пленки (АП) с оптическими и теплофизическими свойствами, близкими к монокристаллам алмаза (теплопроводность @18-20 Вт/смЧК [1] и коэффициент поглощения @5410-2 см-1, показатель преломления n=2,38-2,42 для 1=10,6 мкм). Значительный интерес к использованию подобных алмазных пластин толщиной до 1-2 мм и площадью до 100 см2 в качестве выходных окон для СО2 лазеров мощностью 10-20 кВт [2] обусловлен их более высокими порогами тепловой стабильности и разрушения, чем у традиционных материалов ИК оптики (ZnSe, KC1 и др.). Однако задача создания более сложных оптических устройств оставалась нерешенной по двум основным причинам. Во-первых, механическая обработка АП с целью получения требуемого профиля затруд нена из-за высокой твердости алмаза. Во-вторых, относительно малая толщина алмазных пластин не позволяет получать традиционным способом оптические элементы с достаточной апертурой. В качестве альтернативы, в работах [3] предлагается использовать АП в качестве подложек дифракционных оптических элементов [4], фазовый рельеф которых формируется методом селективного лазерного травления, разработанного в Институте общей физики РАН. Другой проблемой являются относительно высокие потери энергии, связанные с френелевским отражением, что существенно при фокусировке излучения мощных технологических СО2-лазе-ров. Относительно высокий показатель преломления алмаза приводит к тому, что из-за потерь на отражение пропускание алмазной пластины на длине волны 10.6 мкм не превышает 71%. Поэтому, особую актуальность приобретает задача просветления АП.

n=1

кк

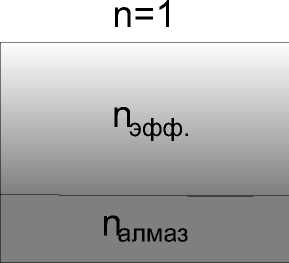
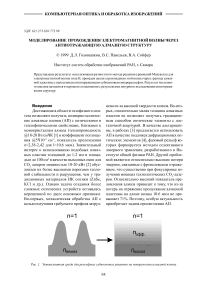
Рис. 1. Эквивалентная среда для рельефных субволновых решеток на поверхности алмазной пленки

Обычные пленочные антиотражающие покрытия значительно уступают алмазу по своим свойствам, что не позволяет использовать в полной мере уникальные свойства АП. В работах [5,6] на результатах натурного эксперимента продемонстрирована эффективность антиотражающих субволновых периодических микроструктур на поверхности алмазной пленки, созданных также методом селективного лазерного травления. Численный анализ работы антиотражающих структур в [5,6] проводился с помощью теории эффективных сред [7]. В рамках этой теории субволновая дифракционная структура рассматривается как градиентная среда с плавно меняющимся поперечным градиентным распределением показателя преломления (Рис. 1).

Однако, приближение теории эффективных ред не учитывает полностью реальных электромагнитных эффектов.

2. Численное моделирование с помощью разностного решения уравнений Максвелла

Рассмотрим распространение электромагнитной волны через поверхность с нанесенным дифракционным субволновым рельефом. В работе [8] представлена разностная схема для трехмерного уравнения Максвелла, записанного в системе СИ в декартовой системе координат. Так как дифракционный рельеф наносится в виде полос, то выбор декартовой системы координат с осью X, направленной параллельно полосам, позволяет построить следующую двумерную схему для волны типа H:

E_x n + 1

h ; ^{+ 1}

к e ; ^{+ 1}

t ^x

Ц о Ц

h t ( H

Е о Е

V

H ^{+ 1}

17 n + 1

Ex, -1

h y

+ H z ;

z j +1

h y

е

H z

n + 1

, k +1

H n ^{+ 1} 1

hz

+ E x ;

h E^{n + 1} ht    ^x

- e^{; + 1}

x k -1

Ц о Ц

hz

+ H , .

где H_y ,H z ,E_x - соответствующие проекции векторов напряженности электрического и магнитного полей Н и E в декартовой системе координат, e₀,e,m 0 m - диэлектрические и магнитные проницаемости вакуума и среды, h t , h y , h z - шаги дискретизации на сет ^{ке w} ht,hy,hz ^={( y_j ^,z k ^,t n ^{)0D} в области} D={ ⁰ y ^, 0z, 0t}, где j,k,n узлы сетки, причем 0y-2, 0z-2, 0t-2. Для простоты записи у значений полей отображены индексы, отличные от j,k,n. Краевые условия для Ex и H_y первого рода, для Hz второго рода. Полученная схема аппроксимирует краевую задачу с погрешностью аппроксимации O(h_t, h_y, hz). Найдя решение системы разностных уравнений (1) получаем искомое распределение электромагнитного поля в интересующей области.

Численные эксперименты, результаты которых приведены в Таблице 1, состояли в формировании волн типа H (1=10.6 мкм., с цугом в одну ддину волны), падающих на границу раздела пластинка-воздух и моделировании дальнейшего распространения прошедших и отраженных волн. В работе [6] приведены результаты натурного исследования антиотражающей структуры с периодом 3 мкм и глубиной порядка 1.8 -2.0 мкм, реали-

Таблица 1. Сравнение энергии отраженной волны при различных формах дифракционного рельефа

Номер численного эксперимента	Форма дифракционного рельефа	Диэлектрическая проницаемость пластинки (Ф/m)	доля отраженной энергии (%)
1	без дифракционного рельефа	5,6644	17,2
2	треугольник с базисом 4 мкм. и высотой 2,5 мкм.	5,6644	12,5
3	треугольник с базисом 3 мкм. и высотой 2,5 мкм.	5,76	9,65
4	треугольник с базисом 2 мкм. и высотой 2,5 мкм.	5,76	8,68

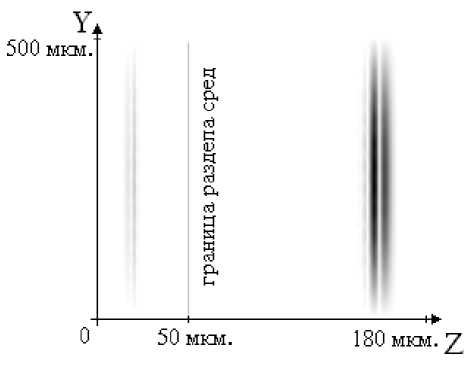
Рис. 2. Распределение модуля амплитуды электрической составляющей электромагнитного поля прошедшей и отраженной волны зованной на алмазной пластине. Максимальное увеличение пропускания для алмазной пластины, обработанной с одной стороны, достигало »6ё7%, что вполне согласуется с результатами, приведенными в (Таблице 1).

Параметры схемы (1) выбирались следующими : L =500 мкм., L =180 мкм., L t =8,1410^-14 с., h=1/3 мкм., h z =0,2 мкм., h_t=3,5 Ч10^-18 с. Энергия электромагнитного поля определялась[9] как

W = 1 J ^ 0 ^ E\² + д ₀ ^ H "  )ф .

2 _D

На рис. 2 представлено разделение падающей волны ( четвертый эксперимент )на прошедшую через границу раздела пластин-ка-воздух и отраженную от этой границы.

На рисунках (3), (4) показаны фрагменты формирующейся отраженной и прошед-

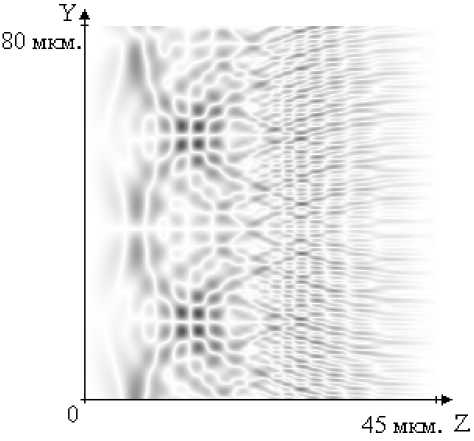
Рис. 3. Фрагмент распределения модуля амплитуды проекции Hz в отраженной волне шей волны, на которых различимы волны типа Н высоких порядков, возникшие в дифракционном рельефе.

Заключение

В данной работе показана возможность использования разностного решения уравнений Максвелла для анализа работы антиотражающих алмазных субволновых структур. Результаты проведенного численного моделирования находятся в хорошем согласовании с результатами натурных исследований, опубликованных в [5,6], и результатами численного анализа с помощью теории эффективных сред второго порядка [6,7]. Таким образом, разностное решение уравнение Максвел-

Рис. 4. Фрагмент распределения модуля амплитуды проекции H z в прошедшей волне

ла впервые позволило провести моделирование алмазных антиотражающих структур и оценить их эффективность в рамках теории электромагнитного поля, а также провести анализ тонкой структуры отраженной электромагнитной волны.