Моделирование прохождения света в массивах металлических наностержней

Металлические частицы с размерами от 5 нм до нескольких сотен нанометров, распределенные периодично или случайно на диэлектрической подложке, или слои таких частиц имеют интересные оптические свойства и изучались долгое время [1]. В последнее время расширились возможности по изготовлению таких систем с периодичным распределением одинаковых сфер. В зависимости от размера и распределения сфер они могут быть очень хорошими поглотителями света [2, 3] или фотонными кристаллами, действующими как непоглощающие зеркала в определенном частотном диапазоне электромагнитного спектра [4].

Такие структуры являются композитными средами, включающими два и более различных материала с характерными размерами включений, много меньшими длины волны падающего света. Для анализа подобных структур применяют теорию эффективных сред (ТЭС) в виде соотношений Максвелла-Гарнета [5], когда один из компонентов может рассматриваться как основной, в который встроены включения другого материала. Они предполагают точное вычисление поля в однородном основном материале, произведенном одиночным сферическим или эллиптическим включением, и модификацию его с учетом взаимодействия между включениями. Теория Максвелла-Гарнета пригодна для низких концентраций (менее 30 %) относительно маленьких наночастиц (до нескольких десятков нанометров).

В [6] предложен метод расчета эффективной диэлектрической проницаемости композитной среды на основе детального учета запаздывания радиационного взаимодействия между составляющими среду сферическими частицами, расстояние между которыми сопоставимо с длиной волны излучения. Представленный метод позволяет рассчитывать оптические свойства композитных сред, в которых расстояние между частицами сопоставимо с длиной волны внешнего излучения. Исследования сферических серебряных включений в диэлектрическую среду показали влияние радиуса сфер и расстояний между ними на отклонение результатов теории Максвелла-Гарнета от решения, учитывающего зависимость оптических свойств металлических наношаров от их размеров. В частности, для среды с наношарами радиусом 10 нм и концентрацией 10 % отличие в результатах численного расчета показателя преломления композитного материала несущественно. Однако уже при радиусе 20 нм разница достигает нескольких десятков процентов.

В работе [7] было исследовано прохождение ТМи ТЕ - поляризованных волн в двумерных массивах серебряных наностержней различного диаметра в желатиновой среде. Авторы провели сравнение метода рекурсивных функций Грина с теорией Мак-свелла-Гарнета на примере изучения характеристик пропускания периодических и непериодических массивов наностержней. Было показано сильное влияние взаимодействия между наностержнями, вкладов мультиполей и формирования фотонных запрещенных зон на оптические спектры, что не может быть учтено в рамках классической ТЭС. Авторы отметили частичную адекватность теории Максвелла-Гарнета для ТМ - поляризованного света и ее непригодность для случая ТЕ - поляризации.

В [8] на основе матриц переноса был проведен анализ пропускания и отражения электромагнитных волн в микроволновом диапазоне периодических массивов тонких металлических проводников с низкой объемной концентрацией (менее 0,5 %). Были исследованы зависимости эффективной диэлектрической проницаемости и поглощения массивов от толщины и проводимости стержней для случая ТЕ -поляризации. Рассчитанная эффективная диэлектрическая проницаемость и плазменная частота качественно совпали с теоретическими моделями.

В дальнейшем численные и теоретические работы показали, что значения эффективной диэлектрической проницаемости различаются для материалов с конечной и бесконечной проводимостью. В работе [9] объясняется различие в характеристиках эффективной среды сверхпроводящих и с конечной проводимостью решеток с малым периодом (относительно длины волны). Для решеток с конечной проводимостью, в отличие от сверхпроводящих решеток, векторные компоненты электромагнитного поля могут быть полностью усреднены. Как следствие, две возможные эффективные среды могут быть описаны, если размеры элементов решетки много больше или меньше, чем глубина проникновения поля внутрь металла.

В [10, 11] была предложена нелокальная модель (НМ) однородной среды для периодичных массивов длинных тонких стержней с отрицательной диэлектрической постоянной, упорядоченных в периодической квадратной сетке, на основе определения поляризуемости одиночного стержня и применения методов интегральных уравнений. Исследование модели было проведено для низких концентраций непоглощающих стрежней (менее 0,8 %) и малого их радиуса (до 12 нм для видимого диапазона). Сравнение результатов моделирования задачи отражения на конечной пластине со стержнями, ориентированными параллельно поверхности пластины, полученных с использованием НМ и электромагнитного подхода, показало адекватность подхода для ТЕ - и ТМ - поляризаций.

В данной работе проверяется способность НМ описывать структуры со стержнями конечной проводимости с размерами меньше и больше глубины скин-слоя материала стержней.

Модель эффективной диэлектрической проницаемости

В работе [11] рассматривается матрица из диэлектрического материала с двумерной решеткой наностержней с отрицательной диэлектрической постоянной. Радиус стержней R , они расположены в квадратной сетке, расстояние между стержнями (постоянная сетки) a . Диэлектрическая постоянная стержней e m . Диэлектрическая постоянная материала e h . В данной работе рассматривается распространение монохроматических полей с временной зависимостью вида e ^{+ j a t} .Структура бесконечна по оси z , поэтому решение уравнений Максвелла разделяется на ТЕ - (вектор магнитного поля параллелен z ) и ТМ - (вектор электрического поля параллелен z ) случаи.

В [11] было показано, что для длин волн много больших радиуса стержней поле в композитной периодической структуре может быть описано с использованием нелокальной диэлектрической прони-

Вывод НМ производится в следующих предположениях: стержни очень тонкие ( R / a << 1), их объемная концентрация мала ( f << 1), и расстояние между ними мало ( a <<  2 ).

Заметим, что в [10, 11] (1) для e _TE приводится только для стационарного предела ( k = 0 и в = 0), тогда как (2) для e _TM выводится для динамического случая при k x , k y = 0.

Из (2) следует, что среда обладает пространственной дисперсией. Так, диэлектрическая проницаемость зависит не только от частоты падающего света в , но и от компонента волнового вектора, параллельного стержням. Предложенная модель также действует для диэлектриков с положительной вещественной частью диэлектрической проницаемости.

Массивы наностержней в диэлектрической пластине

Для проверки предложенной модели эффективной диэлектрической проницаемости мы рассмотрим прохождение плоской волны для случаев ТЕ-поляризованной волны ( E_z = 0) и ТМ-поляризованной волны ( H z = 0) с длиной волны 2 = 0,5 мкм через диэлектрическую пластину с металлическими стержнями (рис. 1). Структура периодична по оси y и бесконечна по оси z . Диэлектрическая проницаемость пластины e h = 2,25, ее толщина d = 2,7 мкм. Материал стержней - серебро ( e _m = - 9,49 + 1,483i). Для простоты мы ограничимся нормальным падением волны ( k z , k y = 0).

_k inc

воздух e = 1

воздух e = 1

y цаемости:

zx

а те

= ^а h

2а h

1аm +аh - 1 fаm-аh а TM (®, kz ) а h

h

а h в2 — kz

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^™  ^^^^^^в  ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^_

(а m —а h ) f вР

где а _TM , а _те - диэлектрические проницаемости для

ТМ - и ТЕ - поляризаций, f = nR2/a2 - концентрация стержней, kz - z-компонента волнового вектора, в = ю^аhц0 - волновое число в диэлектрической структуре, вр - плазменное волновое число для идеально проводящих стержней приводится в [10]:

(вpa)2 *            --------- ln I — | + 0,5275

I 2пR )

Рис. 1. Массивы серебряных наностержней в диэлектрической пластине

Далее, для демонстрации точности теоретических результатов, проведена серия численных экспериментов моделирования дифракции света на структуре с представленной геометрией с вариацией значений концентрации стержней f от 0 % до 100 %. Содержание стержней 100 % соответствует полностью металлической пластине, содержание 0 % - полностью диэлектрической. Отметим, что перекрытие цилиндров происходит при f > 78,5 %, поэтому на данном интервале проводился один численный эксперимент с f = 100 %. Для экспериментов были использованы стрежни радиусом R, равным 3 нм и 30 нм. Для металлов с конечной проводимостью электромагнитное поле всегда проникает внутрь некоторого тонкого слоя, извест- ного как скин-слой. Глубина скин-слоя серебра в диэлектрике на длине волны 0,5 мкм составляет величину порядка Х/30 (т.е. 17 нм) [9], так что ширина стержней малого радиуса меньше глубины скин-слоя, и ширина стержней большего радиуса больше глубины скин-слоя. Выбор значений радиуса стержней был продиктован значительным отличием поляризационных характеристик маленьких и больших наночастиц [12]. Если наночастица достаточно мала (R << X), то, в соответствии с теорией Ми, вклад в спектр поглощения дают только дипольные плазмонные колебания. Тогда как для больших частиц вклад в спектр дают также и резонансы высокого порядка. Когда наноразмерная частица освещается светом, электрическая компонента электромагнитного поля возбуждает коллективные колебания электронной плазмы внутри частиц - плазмоны. Если частицы расположены в цепочки, эти плазмонные колебания принимают резонансный характер, что облегчает прохождение волн резонансных частот. Такие цепочки исследовались в литературе [11, 13] как потенциальные кандидаты для субволнового волноводного распространения света.

Эффективная диэлектрическая проницаемость рассчитывалась по формулам (1) и (2). Объединенным методом конечных элементов - граничных элементов (ПМКЭ-ГЭ) для периодических структур [14] проводилось моделирование прохождения плоской волны через пластину с вычисленной эффективной диэлектрической проницаемостью. Результаты моделирования были сравнены с результатами моделирования этим же методом на структуре с детальной геометрией стержней.

Случай TМ - поляризации

Зависимости пропускания и отражения ТМ - волны от объемной концентрации f через пластину с массивом стержней радиусом 3 нм представлены на

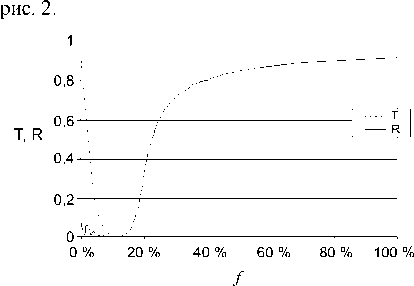
Рис. 2. Коэффициенты пропускания (T) и отражения (R) прохождения ТМ - волны через пластину с массивом стержней радиусом 3 нм

Из графика можно выделить область с высоким поглощением и низким отражением вблизи f = 11 %. Реальная часть комплексного эффективного показателя преломления, соответствующего позиции резонанса, становится близкой к показателю окружаю-

щей среды, что минимизирует дифракцию и отражение на структуре. Мнимая часть эффективного показателя преломления отлична от нуля, что приводит к поглощению проходящей волны. Степень поглощения зависит от толщины пластины. Другая область с f < 11 % может быть охарактеризована осцилляцией коэффициента отражения, вызванной интерференцией отраженных от граней пластины волн.

Зависимости пропускания и отражения ТМ - волны от объемной концентрации f через пластину с массивом стержней радиусом 30 нм представлены на рис. 3. Осцилляции коэффициента отражения при f < 6 % более выражены, чем в случае стержней малого радиуса. Основная причина - это резонансные свойства цепочек стержней. Поле внутри больших стержней стремится к нулю, увеличивая отражение от них. В свою очередь, условия резонанса зависят от расстояния между стержнями.

a)

б)

R

T

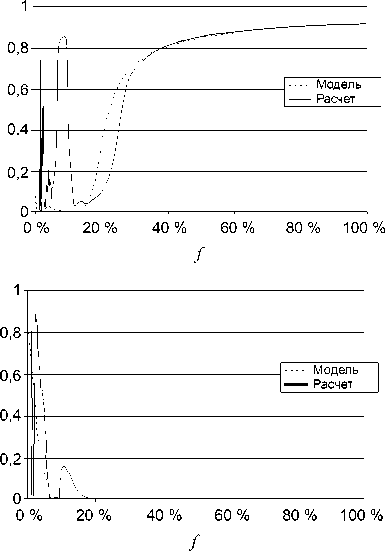
Рис. 3. Коэффициенты отражения (а) и пропускания (б) прохождения ТМ - волны через пластину с массивом стержней радиусом 30 нм

Когда расстояние а между стержнями равно или меньше половины длины волны в диэлектрической пластине, пропускание приближается к нулю и отражение увеличивается до максимума (см. область с f > 18 %).

На рис. 4 изображены примеры точных численных расчетов для некоторых значений объемных концентраций стержней с радиусом 30 нм. Интенсивность инвертирована.

Значения коэффициентов отражения R и пропускания T для приведенных объемных концентраций стержней следующие: а) f = 1,44 %, R = 0,007, Т = 0,59; б) f = 2,66 %, R = 0,04, Т = 0,91; в) f = 9 %, R = 0,85, Т = 10-5. При низких объемных концентра- циях стержней и соответственно больших расстояниях между ними по сравнению с длиной волны электромагнитное поле проходит между стержнями, формируя резонансные структуры. Распределения поля такого рода не могут быть усреднены. С увеличением объемной концентрации поле становится

Рис. 4. Распределение интенсивности прохождения ТМ -волны через пластину с металлическими стержнями с объемными концентрациями:

а) f = 1,44 %; б) f = 2,66 %; в) f = 9 %

Отклонения интенсивностей отраженной и пройденной волн A R и A T нулевых порядков дифракции, рассчитанных точным моделированием структуры, от коэффициентов, рассчитанных моделированием пластины с эффективной диэлектрической проницаемостью, вычисленной с помощью (2), определяется как:

A R = | R_m - R_e\ и A T = T - T e | , где R m , T_m - коэффициенты отражения и пропускания однородной пластины с эффективной диэлектрической проницаемостью; R e , T_e - коэффициенты диэлектрической пластины с металлическими стержнями.

На рис. 5 приведены зависимости суммы отклонений коэффициентов A R и A T от относительного расстояния между стержнями аI X для структур со стержнями радиусом 3 нм и 30 нм. Сумма отклонений возрастает с увеличением расстояния аI X . При расстоянии между стержнями, большем X I6, сумма отклонений коэффициентов превышает 0,025.

На рис. 6 приведены зависимости суммы отклонений коэффициентов A R и A T от объемной концентрации стержней для ТЕ - случая. Несмотря на то, что НМ работает при условии малости концентрации f, видно, что сумма отклонений для стержней с малым радиусом менее 0,02 при f > 4 %, для стержней с большим радиусом при f > 30 %. Таким образом, НМ применима на всем диапазоне объемных концентраций для моделирования массивов стержней малого радиуса в ТМ - случае.

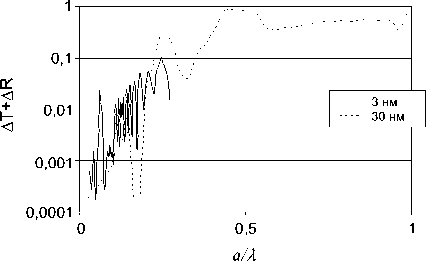
Рис. 5. Зависимость суммы отклонений коэффициентов пропускания и отражения ТМ - волны от a/ λ

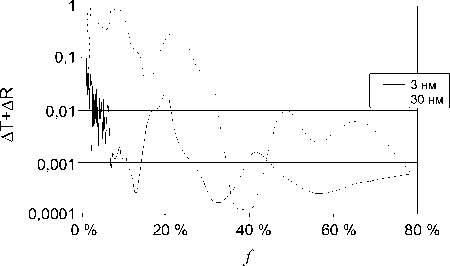
Рис. 6. Зависимость суммы отклонений коэффициентов пропускания и отражения ТМ - волны от концентрации стержней f

Случай TЕ - поляризации

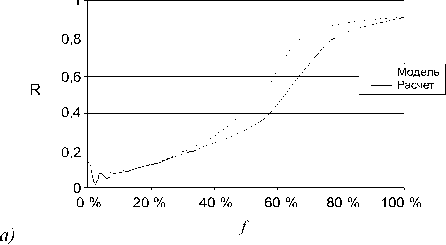
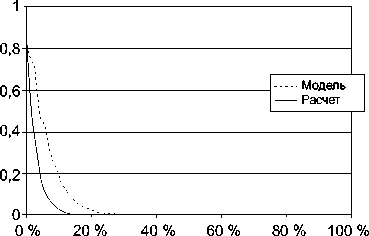
Зависимости пропускания и отражения ТЕ - волны от объемной концентрации f через пластину с массивом стержней радиусом 3 нм представлены на рис. 7.

Здесь также можно выделить область с осцилляцией коэффициента отражения при f < 20 % (с использованием модели), причины которой схожи с причинами осцилляции в ТМ - случае. Точное моделирование показало, что осцилляции затухают к f ~ 11 % и имеют меньшую амплитуду (рис. 7, а). С другой стороны, величина пропускания, рассчитанная точным моделированием, меньше пропускания, рассчитанного с помощью модели (рис. 7, б). Предполагается, что пластина с усредненным материалом с эффективной диэлектрической проницаемостью, вычисленной по (1), имеет меньшее поглощение, чем фактическая структура.

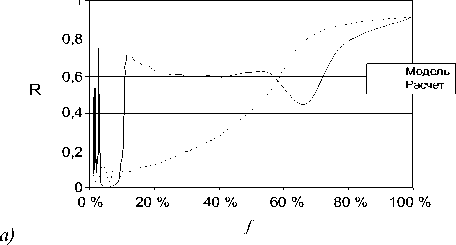
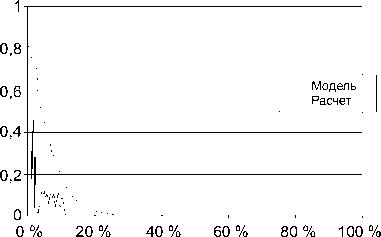
Коэффициенты пропускания и поглощения в случае стержней радиусом 30 нм полностью различны (рис. 8).

б)

f

в)

а)

б)

Рис. 9. Распределение интенсивности прохождения ТЕ - волны через пластину с металлическими стержнями с объемными концентрациями: а) f = 2,57 %; б) f = 2,62 %; в) f = 2,67 %

Рис. 7. Коэффициенты отражения (а) и пропускания (б) прохождения ТЕ - волны через пластину с массивом стержней радиусом 3 нм

f

Рис. 8. Коэффициенты отражения (а) и пропускания (б) прохождения ТЕ - волны через пластину с массивом

б)

стержней радиусом 30 нм

Здесь можно выделить область f > 11 % с высоким отражением. Расстояние между стержнями для этой области между 0 и X/2. Другие области высокого отражения соответствуют расстояниям X, 5/4X, 3/2X. Таким образом, структура представляет собой двумерный фотонный кристалл.

На рис. 9 изображены примеры точных численных расчетов для некоторых значений объемных концен траций стержней. При малых объемных концентрациях стержней также формируются резонансные структуры поля.

Значения коэффициентов отражения R и пропускания T для приведенных объемных концентраций стержней следующие: а) f = 2,57 %, R = 0,52, Т = 0,16; б) f = 2,62 %, R = 0,19, Т = 0,29; в) f = 2,67 %, R = 0,74, Т = 0,05. Можно отметить, что малые вариации объемной концентрации приводят к большим изменениям коэффициентов.

Сумма отклонений коэффициентов A R и A T для стержней радиусом 3 нм превышает 0,007 (рис. 10). Для стержней радиусом 30 нм минимальная сумма отклонений на порядок больше и составляет 0,1.

Для стержней радиусом до X/100 отклонение суммы коэффициентов отражения и пропускания на интервале объемной концентрации стержней от 0 % до 100 % не превышает 0,32. Для стержней радиусом более X/10 максимальная сумма отклонений составляет 1,38 для обеих поляризаций.

На рис. 11 приведены зависимости суммы отклонений коэффициентов A R и A T от объемной концентрации стержней для ТЕ - случая. Здесь сумма отклонений для стержней с малым радиусом менее 0,02 в небольшом диапазоне концентрации 20 % <  f < 36 %.

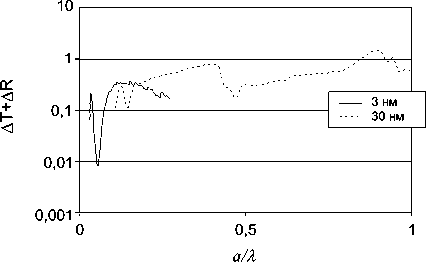
Рис. 10. Зависимость суммы отклонений коэффициентов пропускания и отражения ТЕ - волны от a/ λ

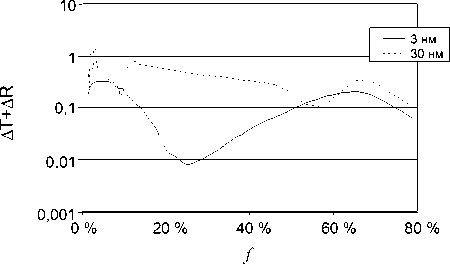
Рис. 11. Зависимость суммы отклонений коэффициентов пропускания и отражения ТЕ - волны от концентрации стержней f

Для стержней большого радиуса сумма не опускается ниже 0,1 на всем диапазоне концентрации. Таким образом, НМ применима только для качественного моделирования массивов стержней малого радиуса в ТЕ - случае.

Заключение

Двумерные массивы серебряных наностержней в диэлектрической пластине обладают нетривиальными оптическими свойствами. Вследствие малых по сравнению с длиной волны размерами такие структуры должны моделироваться с использованием точной электромагнитной теории. На ее основе построены модели усреднения материала, в частности, рассматривается НМ усреднения. Результаты аналитического моделирования сравниваются с анализом распространения света через точную структуру численным периодическим методом конечных – граничных элементов. Сравнение показало эффективность НМ в ТМ - случае для расчета структур с металлическими стержнями. Сумма отклонений коэффициентов отражения и пропускания возрастает с расстоянием между стержнями. В ТЕ - случае модель может быть использована только для качественного анализа.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-SA-06), гранта РФФИ 08-07-99007- р_офи, Фонда содействия отечественной науке и гранта Президента РФ поддержки ведущих научных школ (НШ-3086.2008.9).