Моделирование производства в обрабатывающем секторе с учетом дефицита оборотных средств

Обрабатывающий сектор российской экономики функционирует в условиях неэффективности и жесткой конкуренции с импортом. Причина этого – исторически сложившиеся условия развития сектора, который сформировался в закрытой административнорегулируемой экономической системе советского периода в отсутствие конкуренции с импортом. В настоящее время с поддержанием функционирования обрабатывающего сектора связана существенная часть расходов государственного бюджета. Оптимизация бюджетных расходов требует реализации программ модернизации предприятий обрабатывающего сектора. Анализ экономических последствий реализации таких программ должен проводиться с учетом особенностей функционирования сектора и возможных косвенных последствий принимаемых экономических решений. Примером неудачной экономической программы модернизации является политика «ускорения» второй половины 80-х годов прошлого века, которая привела к перестройке и финансовой разбалансированности экономики. Адекватным инструментом для анализа последствий реализации таких программ являются математические модели, описывающие деятельность производства в обрабатывающем секторе с учетом особенностей его функционирования в российских экономических условиях. Среди таких особенностей следует выделить нестабильность реализации продукции в условиях конкуренции с импортом и возникающий в результате дефицит оборотных средств, который покрывается за счет различных форм кредитов и субсидий. В этих условиях показатели деятельности производственных компаний обрабатывающего сектора оказываются существенно зависящими от кредитных рейтингов. Снижение кредитного рейтинга в результате падения спроса или роста процентных ставок в условиях квазистабиль-ной финансовой ситуации приводит к падению рыночной капитализации компаний и, как следствие, к дальнейшему росту процентных ставок по кредитам, что влечет за собой дальнейшее ухудшение показателей деятельности компаний в условиях дефицита оборотных средств. Одним из основных показателей, характеризующих положение компании, является ее капитализация, являющаяся залогом при кредитовании оборотных фондов. Поэтому актуальной задачей является разработка методов оценки и прогнозирования уровня капитализации компаний, функционирующих в условиях нестабильного спроса, основанных на анализе показателей их деятельности.

С конца 90-х годов прошлого века авторами разрабатывается класс моделей производства с учетом дефицита оборотных средств и нестабильности реализации продукции, основанный на модели Хаутеккера–Иохансена функционирования производства и позволяющий учесть влияние оборотных средств на показатели деятельности компании. За прошедший период создана система математических моделей [1–6], последовательно описывающая экономические механизмы адаптации предприятий обрабатывающего сектора на различных этапах развития российской экономики (льготные кредиты до начала периода высокой инфляции, неплатежи в период дефицита денежной массы и высокой инфляции, сегментированный кредит внутри финансово-промышленных групп, пополнение оборотных средств на конкурентном рынке краткосрочных кредитов в условиях неразвитой торговой инфраструктуры).

2.    Результаты исследования модели с учетом дефицита оборотных средств и ограничения торговой инфраструктуры. Идентификация и верификация модели

В [7] разработана версия модели, учитывающая влияние торговой инфраструктуры и отражающая специфику функционирования предприятий сектора в период квазистабиль-ных экономических условий 2008–2014 гг. Модель позволяет анализировать влияние параметров экономической конъюнктуры на оценку фундаментальной составляющей капитализации компании и может применяться для оценки кредитоспособности компаний, функционирующих в условиях дефицита оборотных средств и нестабильного спроса в квазиста- бильной экономической ситуации. Базовыми предположениями модели являются ограничение сверху Y ∗ на максимально допустимый объем единовременно реализуемой партии товара (ограничение торговой инфраструктуры), нестабильность реализации продукции (моменты реализации продукции образуют пуассоновский поток с параметром λ) и возможность пополнения оборотных фондов на конкурентном рынке краткосрочных кредитов. Обозначим Yq: - текущий запас продукции на производственном складе, п — мощность производства, выпускающего однородную продукцию, y – себестоимость выпуска единицы продукта, p – цена продукта. Предположим, что авансирование производственной деятельности возможно исключительно за счет краткосрочной кредитной линии K(t) под процент r в течение выбранного собственником производства периода времени τ . Тогда K(t) = упӨ(т — t), выпуск к моменту времени t равен Y(t) = Yq + п min(tr), а ссудная задолженность L (t) = ny ^et1 — er(1 т)+). Задача собственника производства заключается в выборе времени τ, в течение которого авансируются производственные затраты за счет кредита, с целью максимизации математического ожидания дисконтированного с коэффициентом А дохода W(Yq) от реализации продукции:

+ОО

W ( Y ) ) = sup т > Q

j Хе ^{- ( А +Д) 1 [} p min ( Y ( t ) ,Y * ) — L ( t ) + W ⁽ ( Y ( t ) — Y * ) + )] dt. q

Решение W(Yq ) уравнения Беллмана (1) характеризует стоимость фирмы с запасом Yq , исходя из производственных характеристик компании. В [7] доказано, что при выполнении

А +Д

А +Д — г

условий рентабельности Х + А > r, Y* > 0, p > у уравнение (1) имеет единствен-

ное решение в классе непрерывных, неотрицательных, неубывающих, вогнутых функций, ограниченных вместе со своей производной на полуинтервале [0, + то). Решение уравнения (1) найдено в явном виде. Соответствующее решению оптимальное поведение производителя описывается следующим образом: в условиях отсутствия реализации продукции производство работает на полную мощность за счет кредита до достижения величины запаса (Zq + 1) Y*, а далее останавливается до момента реализации. Решение уравнения Беллмана позволяет определить [7]

отношение капитализации компании к величине оборотных средств цию параметров модели и величины Z Q .

AW (Q) yη

как функ-

Официальная отчетность компаний отражает усредненные показатели их деятельности. Поэтому решение задачи идентификации требует вычисления усредненных показателей деятельности компании в терминах модели. Вычисление усредненных показателей в модели основано на анализе марковского случайного процесса динамики товарных запасов на складе: X ( x,t ) : X ( x, 0) = x, X ( x,t ) G [0 , ( Z q + 1) Y * ] ■ Доказано, что случайный процесс X ( x,t ) является эргодическим (любое начальное распределение сходится к финальному распределению) [8]. С целью интерпретации модельных показателей в терминах официальной статистики, которая предоставляет усредненные по времени данные, предложена методика вычисления показателей деятельности производства в модели – усреднение по финальному распределению вероятностей изменения запаса. На основе анализа случайного процесса динамики запаса на складе получены явные выражения для средней загрузки и , средних товарных запасов Q и среднего долга компании L t [8, 9]. Результаты решения уравнения Беллмана (1) и анализа случайного процесса динамики запаса на складе позволяют выписать систему уравнений модели (три алгебраических уравнения), экзогенные (входные) и эндогенные переменные которой интерпретируемы в терминах официальной статистики. Система уравнений модели для диапазона значений 0 < Z Q <  2 приведена в [9]. Проведенные расчеты по модели подтверждают, что анализ решений системы в данном диапазоне оказывается достаточным для целей исследования. Набор основных эндогенных

(рассчитываемых) переменных модели, определяющих базовую точку для выбранного года, следующий:

• 1)    λ — рыночная конъюнктура (параметр пуассоновского процесса),

• 2)    ζ 0 — характеристика оптимального запаса,

• 3)    ^λY _η ^∗ — характеристика производственных возможностей при ограничении торговой инфраструктуры.

Набор экзогенных параметров системы уравнений модели, наблюдаемых официальной статистикой:

• 1)    r — процентная ставка по кредитам,

• 2)    A — коэффициент дисконтирования дохода собственника, р — у , ^ +^

• 3)    R = --- р—r — рентабельность производства,

• 4)    u — средняя загрузка мощностей производства,

• 5)    _y ^y _u ^Q _η — оборачиваемость товарных запасов производителя.

На основе анализа статистической отчетности компаний предложена методика идентификации экзогенных параметров модели.

• 1.    Рентабельность R в году t рассчитывается на основе данных консолидированного отчета о прибылях и убытках МСФО в году t :

  R =

  
  

• 2.    Оборачиваемость товарных запасов:

• 3.    Средняя загрузка производственных мощностей u рассчитывается на основе данных об использовании мощностей компании и объемов производства (или структуре выручки при отсутствии данных о структуре производства) по основным видам продукции (источники – годовые отчеты компаний и отчетность МСФО). В табл. 1 приведены данные для расчета средней загрузки производства ПАО КАМАЗ за 2011 г. Коэффициенты загрузки по типу продукции во втором столбце таблицы получены исходя из данных годового отчета компании ПАО КАМАЗ об использовании производственных мощностей. Третий столбец содержит данные о структуре выручки группы по видам выпускаемой продукции (МСФО ПАО КАМАЗ).

• 4.    Процентная ставка r по кредитам – средневзвешенный по объемам кредитов процент по долгосрочным и краткосрочным кредитам и займам компании (МСФО). Выбор такого усредненного процента базируется на результатах анализа статистической отчетности крупных автомобилестроительных компаний, из которой следует, что в условиях квази-стабильной экономической ситуации кредиты использовались в основном на пополнение оборотных средств предприятий. Однако в каждом конкретном случае расчет параметра r

Ф t — C t — SGA t — RD t — F t

Ф t где Фt — выручка, Ct — себестоимость реализации, SGAt — сумма коммерческих расходов и общих и административных расходов, RDt — расходы на исследования и разработки, Ft — чистые финансовые расходы (сальдо финансовых расходов и доходов).

^yQ =          Z t - Z t — 1

yun C t + SGA t + RD t + ( Z t - Z t - 1 )

где Z _t — итого запас в году (МСФО).

Средняя загрузка u принималась равной средневзвешенному по объемам выручки по типам продукции коэффициенту использования мощностей компании.

Таблица1

Вид выпускаемой продукции Коэффициент использования мощности Выручка по типу продукции, млн руб. грузовые авто и сборочные комплекты 0,638 76 765 запасные части 0,65 13 437 автобусы, прицепная техника и автобетоносмесители 0,5 7331 должен проводиться на основании анализа статей расходования заемных средств компании.

Для компании ПАО КАМАЗ расчет проводился на основе отчетности о долгосрочных и краткосрочных кредитах и займах, содержащей информацию о процентных ставках и объемах кредитов для каждого кредитора компании (МСФО). Исходя из указанных данных рассчитывался средневзвешенный по объемам кредитов процент по краткосрочным rs и долгосрочным ri кредитам компании. Значение параметра r определялось как средневзве- rsVs + riVi Vs + V

шенный процент по объемам краткосрочных V s и долгосрочных V кредитов: r = 5. Дефлятор дохода А - процент по выпущенным облигациям (МСФО).

На рис. 1 приведена схема идентификации и верификации модели по данным базового года.

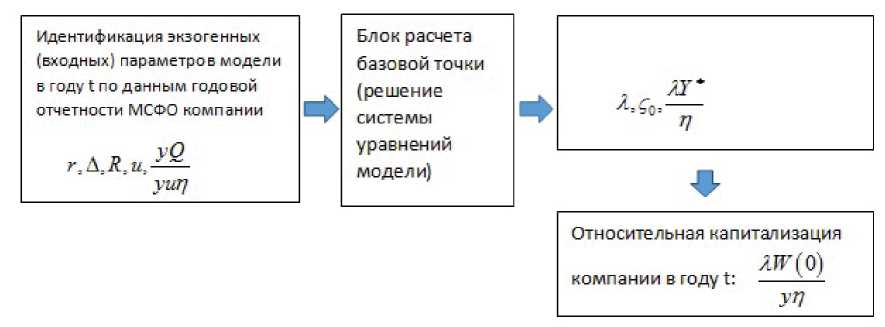
Рис. 1

Таким образом, модель позволяет оценить величину относительной капитализации компании ^WW0) на основе данных о ее производственной деятельности и конъюнктуры в году t, а также методами сравнительной статики [8] провести анализ влияния показателей дея- тельности производства и конъюнктуры на динамику капитализации компании.

Типичными представителями предприятий, функционирующих в условиях дефицита оборотных средств и конкуренции с импортом, являются крупные предприятия автомобильной промышленности. В табл.2и3 приведены результаты идентификации и верификации модели по данным компании ПАО КАМАЗ (Татарстан) за 2011–2014 гг.

Вступление России в ВТО в 2012 г. ужесточило конкурентную борьбу на внутреннем автомобильном рынке, компенсировать негативные последствия которой отчасти удалось введением утилизационного сбора. Государство гарантировало российским автопроизводителям ежегодную компенсацию в размере начисленного компании утилизационного сбора, в то время как поставщики импортных автомобилей вынуждены оплачивать этот сбор полностью, что приводит к увеличению стоимости автомобилей. К 2014 г. финансовая нестабильность и рост валютных курсов привели к снижению спроса и росту себестоимости выпуска продукции компании и, как следствие, к существенному снижению капитализа- ции компании. Государство, осознавая сложность ситуации, поддерживает ПАО КАМАЗ с помощью госзаказа и субсидий. В результате наблюдается существенное расхождение ожиданий рынка и реальных показателей деятельности компании. Объяснение этих расхождений возможно с позиций теории рефлексивности Дж. Сороса [10], содержащей подробный гуманитарный анализ фундаментальной (основанной на показателях деятельности и экономической конъюнктуре) и спекулятивной (основанной на ожиданиях рынка) составляющих рыночной капитализации компании и механизмов взаимного влияния этих составляющих.

Разработанная модель позволяет оценить фундаментальную составляющую капитализации компании ^(Ө') в зависимости от показателей ее деятельности и экономической конъюнктуры, а также провести количественный анализ взаимного влияния фундаментальной и спекулятивной составляющих капитализации в условиях квазистабильной экономической ситуации. В терминах модели отражением ожиданий рынка, характеризующим спекулятивную составляющую, является дефлятор дохода компании А . На рис. 2 представлены результаты расчета методом сравнительной статики влияния дефлятора дохода компании А на фундаментальную составляющую капитализации. Проведенные расчеты показывают, что величина А оказывает существенное влияние на капитализацию компании.

Таблица2

Входные параметры	2011	2012	2013	2014
Процентная ставка	0,06	0,08	0,094	0,095
Рентабельность	0,045	0,077	0,06	0,04
Средняя загрузка	0,62	0,67	0,59	0,53
Дефлятор дохода	0,065	0,083	0,094	0,091
Оборачиваемость товарных запасов	0,12	0,14	0,16	0,18

Таблица3

Камаз, базовые точки	2011	2012	2013	2014
z 0	1,41	1,78	0,91	0,48
λ	16,2	15,6	9,7	7,5
λY ∗ /η	0,66	0,72	0,67	0,62
AW (0) / ( yn )	6,5	9,34	3,23	1,53

Отношение капитализации к оборотным фондам (KAMAZ, 2013)

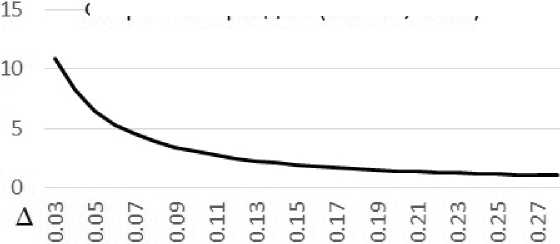
Рис. 2

Предложенная модель позволила провести анализ взаимного влияния фундаментальной составляющей капитализации и дефлятора дохода (ожиданий рынка) в отношении компании ПАО КАМАЗ за период 2011–2014 гг. На рис. 3 на первых двух графиках пунктирная линия соответствует данным статистики (рыночная капитализация компании соответствует усредненным результатам торгов на Московской бирже), жирная линия соответствует базовому сценарию расчетов по модели, тонкая линия соответствует границе рентабельности предприятия (соответствующий дефлятор дохода рассчитан с помощью модели). Граница рентабельности в модели соответствует снижению величины капитализации до уровня оборотных фондов компании.

Анализ построенных зависимостей позволяет сделать следующие выводы. В 2012 г. в условиях ожидания резкого падения продаж (ожидания рынка соответствуют высокому темпу роста дефлятора дохода А ) на фоне вступления в ВТО произошло снижение рыночной капитализации компании при росте фундаментальной составляющей капитализации. Однако ожидания не оправдались, и в 2012 г. наблюдался рост продаж продукции компании (см. график динамики спроса). Это привело к снижению дефлятора дохода А в 2013 г. Падение спроса в 2013 г. и рост процентных ставок привели к существенному снижению фундаментальной составляющей капитализации компании в 2013 г. Дальнейшее падение спроса в условиях наступающего кризиса 2014 г. привело к снижению фундаментальной и рыночной капитализации при замедлении темпа падения величины А . В результате компания в 2014 г. оказалась на границе рентабельности даже в условиях существенной государственной поддержки. В 2015 г. компания оказалась ниже границы рентабельности.

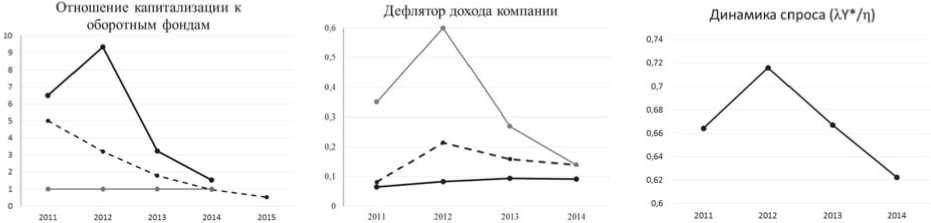
Рис. 3

В кризисной ситуации существенное влияние на показатели деятельности компании начинает оказывать накопленная долговая нагрузка. Поэтому адаптация разработанной модели к экономическим условиям после кризиса 2014 г. требует учета влияния долговой нагрузки на производство.

3. Модификация модели с учетом долговой нагрузки

В кризисных условиях ограничение торговой инфраструктуры не оказывает существенного влияния на показатели деятельности компании, так как в условиях существенного снижения спроса производство начинает работать в основном под заказ. В условиях растущих процентных ставок первоочередной целью собственника производства является погашение задолженности, поэтому дефлятор дохода компании оказывается близким к величине процентной ставки по кредитам компании, т.е. А = r . Пусть L о - начальная задолженность компании, тогда оценка капитализации в зависимости от начального запаса и долга удовлетворяет следующему уравнению Беллмана [8]:

W ( Y о ,L о ) = sup I ( Y ) ,L о ,т ) , т ^ 0

где

+ го

+ pn min( t, т )

- ^y e _e ^rt - e r ^{( t - T} )+) - L о e ^rt ) + +

I ( Y ) ,L о ,т ) = j Xe - ^{( Л + r} ) * о

+ W (c , ( Г ( e ^rt - e ^{r ( t - T ) +} )

+ L о e ^rt -

рҮ о - pn min( t, т

dt.

Обозначим V ( L 0 ) = W (0 , L 0 ) , тогда функция V ( L 0 ) удовлетворяет уравнению

+ го

V ( L 0 ) = sup [ Xe - ^{( A +} r ) t [f pn min( t,T ) - ^ПУ ( e r - e^{T ( t - T ) +} ) - L 0 e r ) +

T > 0                                 r                           +

+ үЦ^- e rt¹ - e r ^{( t - T} ) + r

+ L 0 e ^rt

-

РП min( t, t

) +

dt.

_- pλ

У ⁽ A ⁺ r )

Обозначим q = max

+^), G[0, + to) — множество функций, непрерывных, во гнутых, монотонно убывающих на полуинтервале [0, + то), имеющих ограниченные одно- сторонние производные в точке L0:

dV          dV q С    (L0 + 0) С    (L0 - 0) С -1 VL0 > 0.

dL 0           dL 0

Теорема 1. Пусть выполняется условие рентабельности p >   y M^r и

W (0 , L 0 ) = V ( L 0 ) € G [0 , + то ) , тогда для Vt € [0 , + то ) справедливо соотношение

I ( Y ) ,L 0 ,т ) С lim I ( Y ) ,L 0 ,t ) .

t ^ + го

С экономической точки зрения теорема 1 позволяет сделать вывод о том, что оптимальным в модели является режим безостановочного производства. С математической точки зрения теорема 1 позволяет свести уравнение Беллмана (3) к интегральному уравнению

+ го

V ( L 0 ) = J Xe ^{- ( A +} r ) t [( pnt - ПУ ( e r - 1) - L 0 e ^rt ) + +

+ V

-

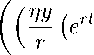
1) ^{+ L} 0 e rt ^-

pnt ₊

dt.

Теорема 2. Решение V ( L 0 ) уравнения (4) для функций из класса G [0 , + то ) при L 0 >  L 0 = n/r ( Р - У ) имеет вид: V ( L 0 ) = V ( L 0 ) + h ( L 0 - L 0 ) , где h € [ q, - 1] •

Теорема 2 утверждает, что оценка стоимости V ( L 0 ) производственной компании при отсутствии запасов является линейной функцией при L 0 >  L 0 . Таким образом, когда задолженность превышает некоторый критический размер, стоимость бизнеса становится отрицательной. В этой ситуации фирма попадает в ситуацию банкротства, а параметр h характеризует сложившуюся практику учета долгов при банкротстве. Теорема 2 позволяет сузить класс функций, в котором ищется решение уравнения (4). Обозначим F ([0 , L 0 ] ,h ) — множество функций из класса G [0 , + то ) , являющихся линейными с коэффициентом - 1 >  h >  q при L 0 >  L 0 .

Введем равномерную метрику в классе F ([0 , L^\, h ) :

р ( ш 1 ,ш 2 )= max |ш i ( x ) - ш 2 ( x ) |, 0 < x С L 0

тогда F ([0 , L 0 ] , h ) является полным метрическим пространством. Пусть B — оператор, соответствующий правой части уравнения (4).

Лемма. Пусть V ( L ₀ ) € F ([0 , L 0 ] ,h ) , тогда BV ( L ₀ ) € F ([0 , L 0 ] ,h ) •

С помощью леммы и принципа сжимающих отображений доказана следующая теорема.

Теорема 3. Уравнение (4) имеет единственное решение в пространстве F ([0 , L 0 ] ,h ) •

Из теоремы 3 следует, что для любого значения параметра h € [ q, - 1] существует единственное решение уравнения Беллмана (2). С экономической точки зрения параметр h можно проинтерпретировать как коэффициент учета долгов при банкротстве компании.

Явный вид решения уравнения (2) найден в классе функций F ([0 , L 0 \, — 1) .

Теорема 4. При h = — 1 аналитическое выражение для оценки стоимости производственной компании имеет вид :

λ              λη

(    У (А + r )\ p- λ .

которого проанализировано влия-

^{w (} Y , , L ^{о )} = А + r^pY > - L 0 ⁺

При h < — 1 построен численный метод, на основе ние коэффициента учета долгов при банкротстве h и процентной ставки r на отношение оценки стоимости компании к оборотным средствам AVVM, которая оказывает влияние на кредитный рейтинг компании.

На рис. 4 представлены зависимости относительной стоимости компании от параметров h и r , рассчитанные с помощью модели на основе данных официальной отчетности компании ПАО КАМАЗ за 2014 г.

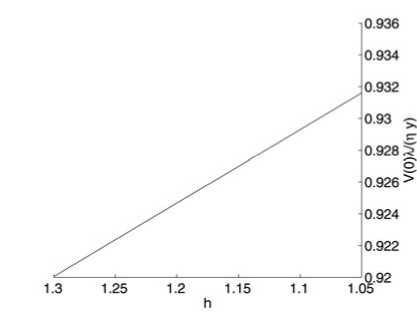
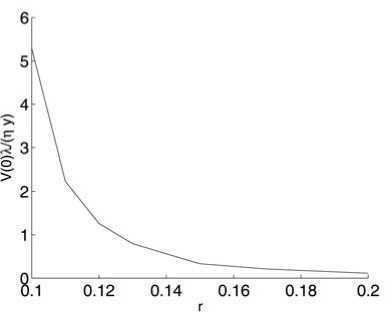
Рис. 4

Из расчетов следует, что изменение параметра h в допустимых пределах не оказывает существенного влияния на оценку относительной стоимости компании без учета начальных запасов и задолженности. Напротив, небольшое увеличение процентной ставки приводит к резкому падению относительной стоимости и соответственно снижению кредитного рейтинга компании. Снижение кредитного рейтинга приводит к увеличению процентной ставки и в дальнейшем к систематическому кризису в отрасли.

Проведенные исследования показывают, что версия модели, учитывающая влияние долговой нагрузки, может быть использована для нахождения критического долга компании, соответствующего границе банкротства и оценки параметра учета долгов при банкротстве компании.

Работа выполнена при поддержке РФФИ № 17-07-00507.