Моделирование пространственных эффектов инновационного развития регионов России

Начиная с Й.А. Шумпетера (Шумпетер, 1982) интерес к проблемам инновационного развития не угасает. Среди ученых, внесших большой вклад в развитие теории инноваций, можно отметить Н.Д. Кондратьева (Кондратьев, 1925), С. Кузнеца1, Г. Менша (Mensch, 1979), В.М. Полтеровича (Пол-терович, 2009), Б.Н. Кузыка, Ю.В. Яковца (Кузык, Яковец, 2005), С.Ю. Глазьева (Глазьев, 2011) и др. В ходе множества исследований рассмотрены различные факторы инновационного развития территорий. Как отмечает Л.Р. Батукова, «инновационная экономика, в силу ее специфики, может быть сформирована только на базе экономического объединения стран достаточно обширного мирового региона, объединение ресурсов и рынков которых позволяет по большей части направлений экономического развития образовать одновременно самодостаточную и не избыточную, устойчиво развивающуюся экономическую систему» (Батукова, 2016).

Теоретический обзор работ по оценке влияния факторов на инновационное развитие территорий показал, что используемые для этих целей инструменты не позволяют установить дифференцированность воздействия данных факторов. Наиболее часто применяющи йся инструментарий – регрес-

S. (1971). Nobel Prize Lecture. Stockholm. URL:

сионный анализ по панельным данным с фиксированными или случайными эффектами – оценивает влияние факторов на исследуемые территории в среднем, не учитывая степень их воздействия. Квантильная регрессия отчасти решает данную проблему, но в то же время не может определить влияние ресурсов, размещенных на окружающих территориях, то есть не оценивает пространственные эффекты, возникающие от воздействия этих территорий. Ключевые факторы инновационного развития территорий, такие как затраты на инновационную деятельность, численность научно-исследовательских кадров и др., влияние которых подтверждено результатами огромного количества исследований, могут оказывать как положительное, так и отрицательное воздействие на инновационную активность предприятий в различных территориальных системах.

Учет пространственного фактора дает возможность выявить направления инновационного развития и сформировать эффективную инновационную экономику сопредельных территорий различного уровня. Использование инструментов пространственного моделирования позволит проверить гипотезу о дифференцированном влиянии факторов, включаемых в производ- https://www.nobelprize.org/prizes/economic- sciences/1971/kuznets/lecture (accessed 01.06.2023).

ственную функцию Кобба – Дугласа, на инновационное развитие регионов России с учетом воздействия окружающих территорий.

Цель настоящего исследования заключается в оценке пространственных особенностей инновационного развития регионов России и моделировании пространственных эффектов, возникающих в результате воздействия окружающих территорий. Для достижения поставленной цели были выдвинуты следующие задачи: провести теоретический обзор работ по оценке влияния факторов на инновационное развитие территорий и в области моделирования пространственных эффектов, возникающих от воздействия окружающих территорий; разработать методический подход к моделированию пространственных эффектов инновационного развития регионов; провести пространственный автокорреляционный анализ инновационной активности предприятий в регионах России и пространственных взаимовлияний между ними для установления основных инновационных центров и зон их влияния; сформировать пространственную модель Дарбина, отражающую зависимости объема отгруженных предприятиями инновационных товаров в регионах России от объема затрат на инновационную деятельность организаций и численности персонала, занятого научными исследованиями и разработками, учитывающую воздействие данных факторов окружающих территорий; оценить влияние рассматриваемых факторов на инновационную деятельность регионов, обладающих высокой концентрацией финансовых и кадровых ресурсов, а также их влияние на инновационное развитие окружающих территорий.

Установленные пространственные эффекты в инновационном развитии от воздействия рассматриваемых факторов в окружающих территориях позволят органам государственной власти сформировать более эффективную политику по поддержке инновационно развивающихся территорий и реализовать Стратегию пространственного развития России, направленную на усиление пространственных взаимосвязей регионов в инновационной сфере.

Теоретико-методические подходы к пространственному моделированию инновационного развития

Наиболее востребованным инструментарием для оценки влияния факторов на инновационное развитие территорий на макроэкономическом и региональном уровнях в научных исследованиях является регрессионный анализ по пространственным, временным и пространственно-временным рядам данных. Такой инструментарий с применением панельных данных использовался, в частности, в работах О.С. Мариева, Е.Д. Игнатьевой, Е.П. Набережневой и И.В. Савина для поиска факторов, оказывающих влияние на инновационное развитие производительных сил в регионах России. Построенная ими модифицированная «функция генерации знаний» Кобба – Дугласа (Мариев и др., 2012) позволила установить ключевые факторы инновационного развития исследуемых регионов и степень их влияния. Следует отметить, что она отражала влияние рассматриваемых факторов в среднем на все субъекты России, однако степень влияния факторов на инновационное развитие каждого региона может значительно отличаться. Более того, некоторые из подтвержденных факторов могут и не оказывать влияния на инновационную активность отдельных регионов. Традиционный регрессионный анализ с использованием панельных данных слабо учитывает пространственную специфику моделируемых процессов.

Регрессионный анализ по панельным данным с фиксированными эффектами использовался А.А. Пушкаревым, Р.И. Грозных и К.М. Нагиевой для изучения факторов, влияющих на патентную активность российских регионов, за период с 2001 по 2014 год (Пушкарев и др., 2018), Е.С. Вандышевой – для оценки степени влияния затрат на технологические инновации, научные исследования и разработки, численности кадров и организаций, занимающихся научными исследованиями и разработками, количества передовых технологий, выданных патентов, числа выпускников, аспирантов и докторантов, а также доли малых предприятий на выпуск инновационных товаров и услуг в 83 регионах России с 2006 по 2015 год (Вандышева, 2017), Л.А. Сосуновой и Е.А. Серпер – для моделирования производственной функции, отражающей влияние научно-технического прогресса на инновационное развитие региональной экономики (Сосунова, Серпер, 2010).

Построенные авторами модели также не учитывают пространственные особенности развития инновационных процессов, не позволяют оценить пространственные эффекты, возникающие от воздействия окружающих территорий. Для их исследования зарубежными авторами применялись инструменты пространственной эконометрики – пространственные авторегрессионные модели. Пространственная модель Дарбина, оценивающая зависимость моделируемых процессов определенной территории от факторов развития данной территории, а также факторов развития окружающих территорий, использовалась, в частности, Y. Xiao, J. Chen, X.-L. Wang, X. Lu для определения пространственных побочных эффектов технологических инноваций и среды обитания (Xiao et al., 2022). Данная модель применялась и для оценки влияния совместных инноваций на качественное развитие экономики (Deng et al., 2023), инноваций в области экологически чистых технологий на интенсивность выбросов углерода (Chen et al., 2023), воздействия инноваций на ценность «зеленого» бренда и пространственного эффекта этого воздействия (Zhang et al., 2023), финансового развития и технологических инноваций на «зеленый» рост (Cao et al., 2022), «зеленых» инноваций на «зеленое» промышленное развитие (Feng, Chen, 2018), цифровой экономики на эффективность промышленных «зеленых» инноваций (Li et al., 2023), инноваций в области «зеленых» технологий на общую производительность «зеленых» факторов (Wang et al., 2020).

В систематизированном виде теоретикометодические подходы к моделированию инновационного развития с учетом пространственных эффектов широко представ- лены в работах зарубежных ученых, с акцентом на «зеленые» инновации. Исследование инновационных механизмов финансовой агломерации, влияющих на скоординированное «зеленое» развитие дельты реки Янцзы в Китае, провели F. Wu, X. Yang, Y. Chen. Используя панельные данные из 41 города в районе дельты реки Янцзы с 2003 по 2019 год, авторы построили модель промежуточных эффектов и пространственную модель Дарбина для оценки влияния финансовой агломерации на скоординированное «зеленое» развитие (Wu et al., 2023).

Необходимо отметить, что пространственная модель Дарбина, используемая зарубежными учеными для оценки пространственных эффектов в инновационном развитии территорий, формировалась только по традиционной матрице пространственных весов – по смежным границам. Результаты их исследований не проверялись другими матрицами пространственного взвешивания, в частности матрицами линейных расстояний между территориями, по автомобильным дорогам и т. д. Выбор матрицы пространственных весов является важным этапом в пространственном моделировании, поскольку может привести к кардинально отличающимся результатам.

Отмеченная проблема была характерна и для исследований российских ученых. В отдельных работах пространственные модели формировались с использованием матрицы пространственных весов по смежным границам, в других – только матрицы линейных расстояний. Среди российских работ по инновационной тематике можно выделить статью А.И. Мосалева (Мосалев, 2022), представляющую исследование оптимального пространственного масштаба межрегионального инновационного сотрудничества. Сформированы различные виды пространственных моделей и определено, что пространственная модель Дарбина (SDM) является наиболее приемлемой моделью с фиксированным эффектом, позволяющей учесть побочный эффект инновационного развития.

Различные модели пространственной регрессии по панельным данным (SAR,

SEM, SDM, SAC) применяли М.В. Шаклеина и К.И. Шаклеин (Шаклеина, Шаклеин, 2022) для моделирования факторов предпринимательской активности в регионах России за период с 2011 по 2019 год. В результате исследования авторами оптимальной пространственной моделью была признана модель пространственного лага и ошибки (SAC). Однако следует отметить, что при ее формировании использовалась матрица обратных расстояний между административными центрами регионов по автомобильным дорогам и железнодорожным путям сообщений. Применение данной матрицы в указанном исследовании было недопустимым, поскольку расстояния между административными центрами регионов, которые использовались для формирования пространственных матриц, менялись за указанный период времени: строились и открывались новые участки автомобильных дорог и железнодорожных путей сообщения, отдельные участки дорог закрывались на реконструкцию.

Учитывая неоднозначность коэффициента пространственной корреляции и высокую неоднородность российских регионов, О.А. Демидова и Э. Камалова применили модифицированную модель Дарбина. Модификация базовой модели состояла в замене коэффициента пространственной автокорреляции и коэффициентов при пространственных лагах независимых переменных на линейные функции от показателей качества институтов рассматриваемого региона. Предложенная модель позволяет выявить зависимость интенсивности пространственных экстерналий от качества институтов региона (Демидова, Камалова, 2021). В данном исследовании при построении пространственной модели также применялась только одна матрица пространственных весов – по смежным границам между регионами. Системное использование пространственных матриц позволило бы авторам более корректно оценить влияние рассматриваемых факторов.

В ходе обзора научной литературы было установлено, что пространственные модели, особенно модель Дарбина, довольно часто используются зарубежными исследователями для оценки влияния факторов на инновационное развитие территорий в условиях высокой пространственной неоднородности. В российских же научных публикациях пространственная модель Дарбина применяется достаточно редко, чаще формируются более простые модели (пространственного лага или ошибки).

Методический подход к моделированию пространственных эффектов инновационного развития регионов

Для оценки пространственных особенностей инновационного развития регионов России и моделирования возникающих пространственных эффектов от воздействия окружающих территорий в работе применялся методический подход, основанный на системном использовании различных инструментов пространственной эконометрики и систем измерения расстояний между территориями.

На начальном этапе исследования для оценки пространственной неоднородности инновационного развития предприятий в России и пространственной кластеризации регионов (поиска формирующихся полюсов роста, пространственных кластеров регионов, похожих по объему отгруженной предприятиями инновационной продукции, а также зон их влияния на окружающие территории) предлагается провести пространственный автокорреляционный анализ по методике П. Морана. В отличие от традиционного подхода планируется использование не одной, а целой системы матриц пространственных весов, в частности смежных границ между регионами, линейных расстояний и расстояний по автомобильным дорогам, протяженности железнодорожных путей сообщения между административными центрами регионов, а также нормированных версий данных матриц. Их совокупное использование поможет получить объективные и надежные результаты, подтвержденные большинством матриц.

Рассчитываемый в ходе пространственного автокорреляционного анализа глобальный индекс Морана позволит оценить схожесть исследуемых регионов, подтвердить возможность их пространственной кластеризации по объему отгруженной инновационной продукции, а локальные индексы Морана – построить диаграмму рассеивания Морана, в которой регионы разделяются на четыре группы. В квадрант HL диаграммы войдут регионы, отличающиеся высоким объемом отгруженных инновационных товаров по сравнению с окружающими регионами, а также полюса роста, обладающие очень высокими значениями по оцениваемому показателю. В данном квадранте мы, в отличие от традиционного подхода, выделяем две подгруппы регионов: полюса инновационного роста с высоким уровнем пространственного взаимовлияния с окружающими регионами (с локальными индексами Морана выше среднего уровня, рассчитанного по их отрицательным значениям), а также потенциальные полюса роста, отличающиеся от окружающих регионов более высоким объемом отгруженных инновационных товаров, но характеризующиеся слабым уровнем пространственного взаимовлияния (с локальными индексами Морана ниже среднего уровня).

Квадрант HH сформируют регионы, обладающие похожим уровнем инновационной активности. Они при развитии тесных межрегиональных взаимосвязей обладают потенциалом для формирования пространственных кластеров. В данном квадранте по уровню пространственного взаимовлияния мы также выделяем две подгруппы регионов: уже формирующие пространственный кластер взаимосвязанных регионов, обладающие высоким уровнем пространственного взаимовлияния на окружающие территории (с локальными индексами Морана выше среднего уровня, рассчитанного по их положительным значениям), а также регионы с низким уровнем пространственного взаимовлияния, которые обладают возможностями в будущем сформировать пространственный инновационный кластер при развитии межрегиональных взаимосвязей.

Квадрант LH диаграммы рассеивания Морана формируют регионы, входящие в зону влияния полюсов роста ( HL ) и пространственных кластеров ( HH ), как правило, располагающиеся вокруг них. Для более детальной оценки степени их влияния в данном квадранте мы также выделяем две подгруппы регионов: территории, испытывающие их сильное влияние (с локальными индексами Морана выше среднего уровня, рассчитанного по их отрицательным значениям), и территории, испытывающие умеренное влияние полюсов роста и пространственных кластеров (с локальными индексами Морана ниже среднего уровня). Такой подход к формированию диаграммы Морана позволит более детально оценить пространственные особенности инновационного развития регионов и предположить наличие пространственных эффектов, возникающих от воздействия окружающих, инновационно развивающихся, территорий.

Для подтверждения наблюдаемых пространственных взаимовлияний между территориями в инновационном развитии на следующем этапе предполагается формирование матрицы Л. Анселина по локальным индексам пространственной автокорреляции (LISA) по различным типам взвешивающих матриц расстояний между регионами России. Выделение в данных матрицах значений пространственной автокорреляции, превышающих средний уровень, рассчитанный отдельно по положительным и отрицательным значениям, позволит установить тесные прямые и обратные пространственные взаимовлияния, а использование различных систем измерений расстояний между территориями – подтвердить объективность полученных результатов. Для оценки пространственных эффектов в инновационном развитии регионов России, которые возникают в результате воздействия окружающих территорий, на следующем этапе планируется построение традиционных регрессионных моделей сквозным (pooled) методом наименьших квадратов, с фиксированными и случайными эффектами (1), а также пространственной модели Дарбина, учитывающей наличие пространственного лага результативного признака и ключевых факторов в модели (2):

Ln(V _it ) = a + ^ + y_t + ftLn(C_it) + P 2 Ln⁽L _lt) + s_it ,  (1)

Ln(V _tt ) = a+p WLn(V_u) + _PWLn(C _tt) +

+ pWLn(L _it) + ^Ln(C it ) + №i(L _it) + E_it ,    (2)

где:

V it – объем отгруженных инновационных товаров, выполненных работ и оказанных услуг по субъектам РФ, млн руб.;

C it – объем затрат на инновационную деятельность организаций в субъекте РФ, млн руб.;

L it – численность всего персонала, занятого научными исследованиями и разработками в субъекте РФ, чел.;

WV it – пространственно взвешенные значения объема отгруженных инновационных товаров, выполненных работ и оказанных услуг, млн руб.;

WLn ( C it ) – пространственно взвешенные значения объема затрат на инновационную деятельность организаций в субъекте РФ, млн руб.;

WLn ( L it ) – пространственно взвешенные значения численности всего персонала, занятого научными исследованиями и разработками в субъекте РФ, чел.;

α – совокупность прочих факторов, влияющих на объем отгруженных товаров;

β – коэффициент эластичности по факторам, включенным в модель;

ρ – коэффициент пространственной авторегрессии;

μ t – индивидуальный эффект региона i , не зависящий от времени t ;

γ t – временные эффекты для региона i в момент времени t ;

ε it – нормально распределенные случайные величины по времени t и территориям i .

Поскольку инновационную активность регионов мы оцениваем по объему отгруженных инновационных товаров, выполненных работ и оказанных услуг, то в качестве ключевых факторов, влияющих на динамику данного показателя, будут рассмотрены факторы, формирующие производственную функцию Кобба – Дугласа, а именно объем затрат на инновационную деятельность организаций и численность всего персонала, занятого научными исследованиями и разработками. При построении регрессионных моделей предполагается использование официальных статистических данных Федеральной службы государственной статистики по 78 регионам России за период с 2000 по 2021 год. Из-за отсутствия данных об инновационной деятельности предприятий из выборки наблюдений предлагается исключить часть регионов, в частности Ненецкий и Чукотский автономные округа, республики Ингушетию, Чечню, Калмыкию, г. Севастополь и Республику Крым. Включение в выборку наблюдений нулевых значений по результативному и факторным признакам этих регионов приведет к некорректным результатам регрессионного анализа. Поскольку при формировании моделей планируется использовать переменные в стоимостном выражении, то для получения корректных результатов объем отгруженных инновационных товаров, работ и услуг, а также затраты предприятий на инновационную деятельность будут очищены от инфляции с помощью индексов потребительских цен и представлены в сопоставимых ценах 2000 года. Перед построением модели планируется также оценка стационарности используемых временных рядов по всем переменным, расчет и анализ описательных статистик. Выбор оптимальной модели из построенных методами сквозной регрессии с фиксированными или случайными эффектами планируется осуществить с использованием стандартных тестов на спецификацию панельных эффектов (Breusch-Pagan и Hausman), информационных критериев, теста Wooldridge на отсутствие автокорреляции в остатках модели, теста Wald на отсутствие гетероскедастичности, теста Pesaran CD – для оценки кросс-секционной зависимости в панельных данных, а также теста Jarque-Bera для проверки гипотезы о нормальном распределении ошибок модели.

Стандартные панельные модели необходимы не только для оценки степени вли- яния производственных факторов на объем отгруженных в регионах инновационных товаров, выполненных работ и оказанных услуг, благодаря использованию коэффициентов эластичности в модели Кобба – Дугласа. Рассчитанное значение константы позволит оценить наличие или отсутствие неучтенных факторов, сделать предположение о наличии пространственного лага в модели, то есть воздействия окружающих территорий на инновационную активность предприятий. Данные модели станут основой для построения пространственной модели Дарбина (SDM), учитывающей пространственные эффекты в динамике объема отгруженных инновационных товаров, работ, услуг, а также пространственные эффекты от воздействия рассматриваемых факторов окружающих территорий (2).

Для построения пространственной модели Дарбина предлагается использовать две матрицы пространственных весов – по смежным границам между регионами и линейным расстояниям между их административными центрами. Данные матрицы в отличие от других, например по автомобильным дорогам и железнодорожным путям сообщений, отличаются постоянством во времени и могут применяться для построения моделей по панельным данным. Модель Дарбина будет сформирована с использованием двушагового метода обобщенных моментов (GMM) с применением инструмента взвешивающей матрицы периода White для контролирования гетероскедастичности, фиксированных эффектов времени с помощью дамми-переменных, а также преобразованием данных с использованием первых разностей. Для подтверждения достоверности модели и тестирования нулевой гипотезы о том, что модель корректна, все параметры регрессии состоятельны, предлагается провести Sargan – Hansen test (J-statistic). Достоверность построенной модели будет оцениваться и с помощью Arellano-Bond serial correlation test, который необходим для проверки нулевой гипотезы об отсутствии автокорреляции возмущений первого и второго порядка, а также Jarque-Bera test на нормальность распределения случайных ошибок в модели. Для выбора оптимальной модели из построенных по двум типам матриц пространственных весов будут использоваться стандартные ошибки моделей, значения информационных критериев Schwarz и Akaike, а также аналог коэффициента детерминации – квадрат корреляции исходных и смоделированных значений по объему отгруженных предприятиями товаров собственного производства, выполненных работ и услуг собственными силами.

Построенная модель позволит скорректировать оценку степени влияния факторов в регионах России на динамику объема отгруженных на их территории инновационных товаров, выполненных работ и оказанных услуг с учетом пространственных эффектов, возникающих в результате воздействия инновационной активности окружающих территорий (благодаря оценке пространственного лага результативного признака в модели), а также влияния рассматриваемых факторов на территории окружающих их регионов (благодаря оценке пространственного лага факторных признаков в модели).

Новизна представленного методического подхода заключается в системном использовании инструментов пространственной эконометрики (пространственного автокорреляционного анализа и пространственной авторегрессии), различных систем измерения расстояний между регионами (матриц пространственных весов). Модели, построенные по различным матрицам пространственных весов, и оценка их параметров позволяют получить более корректные результаты при оценке пространственных эффектов.

Результаты исследования

Проведенные нами исследования показывают, что инновационные процессы в России характеризуются крайне высокой степенью пространственной неоднородности (Наумов, Барыбина, 2020). Это связано с высоким уровнем концентрации в определенных территориальных системах научно-исследовательских кадров, научной инфраструктуры, финансовых ресурсов, направляемых на проведение фундаментальных, прикладных исследований и разработок. На углубление пространственной неоднородности инновационного развития страны оказывают влияние и высокий уровень концентрации обрабатывающих производств в отдельных регионах, уровень социально-экономического развития данных регионов и другие факторы. По данным 2021 года было установлено, что почти 50% всех отгруженных в России инновационных товаров, выполненных работ и оказанных услуг сосредоточены в пяти регионах: г. Москве (12,4%) и г. Санкт-Петербурге (9,7%), Республике Татарстан (12,3%), Московской (7,8%) и Ярославской (6,7%) областях (табл. 1).

Промышленно развитые регионы отличались более умеренным уровнем концентрации отгруженных инновационных товаров, выполненных работ и оказанных услуг.

Так, например, на Свердловскую область по данным 2021 года приходилось всего 3,5% всех отгруженных в России инновационных товаров, Республику Башкортостан – 3,2%, Самарскую область – 3,1%, Нижегородскую область – 2,9%, Тульскую область – 2,1%, Пермский край – 1,4%, Ленинградскую область – 1,2%. В группе регионов, отличающихся уровнем инновационной активности предприятий выше среднего по России, в 2021 году было сконцентрировано 35,7% всех отгруженных инновационных товаров. В остальных 64 субъектах РФ уровень концентрации инновационных товаров, работ и услуг не превысил 16%. Низкий уровень инновационной активности предприятий наблюдался и в регионах, обладающих мощным научно-исследовательским потенциалом. Так, например, в Новосибирской области

Таблица 1. Показатели реализации инновационных товаров, выполненных работ и оказанных услуг по субъектам РФ в 2021 году

Регион	Объем отгруженных инновационных товаров, млн руб.	Уровень концентрации в регионах всех отгруженных в России инновационных товаров, %
г. Москва	795297	12,4
Республика Татарстан	789134	12,3
г. Санкт-Петербург	624053	9,7
Московская область	502758	7,8
Ярославская область	430375	6,7
Всего по группе регионов	3141618	48,9
Свердловская область	227236	3,5
Тюменская область без АО	203462	3,2
Республика Башкортостан	202445	3,2
Самарская область	199173	3,1
Белгородская область	190336	3,0
Нижегородская область	186005	2,9
Мурманская область	149145	2,3
Ростовская область	140659	2,2
Тульская область	134432	2,1
Омская область	123819	1,9
Хабаровский край	96448	1,5
Республика Мордовия	94885	1,5
Красноярский край	92424	1,4
Пермский край	90237	1,4
Оренбургская область	82402	1,3
Ленинградская область	78901	1,2
Всего по группе регионов	2292008	35,7
Источник: составлено авторами.

в 2021 году было отгружено только 0,53% всех инновационных товаров, а Томской области – 0,29%.

Пространственный автокорреляционный анализ по методике П. Морана с использованием восьми матриц пространственных весов подтвердил наличие пространственной неоднородности инновационного развития предприятий в России (рис.).

Регионы, отмеченные красным цветом на диаграмме, а именно г. Москва и г. Санкт-Петербург, Московская, Нижегородская, Тульская, Ярославская и Самарская области, Республика Татарстан, обладают значительным в отличие от окружающих регионов объемом отгруженных инновационных товаров, выполненных работ и оказанных услуг. Данные регионы, отнесенные в результате пространственного автокорреляционного анализа к квадранту HH, характеризуются тесными пространственными взаимовлияниями с окружающими территориальными системами и обладают всеми необходимыми предпосылками для формирования межрегионального инновационного пространственного кластера. Наличие тесных пространственных взаимовлияний между указанными регионами подтвердила сформированная с использованием различных систем измерения расстояний между территориальными системами матрица локальных индексов Л. Анселина (табл. 2).

Данная матрица установила прямые тесные пространственные взаимовлияния между г. Москвой и г. Санкт-Петербургом, Республикой Татарстан, Московской и Ярославской областями, а также обратные взаимовлияния с Владимирской, Ивановской, Калужской, Костромской и Рязанской областями. Пространственные взаимовлияния были установлены и между г. Санкт-Петербургом и Республикой Татарстан, Московской, Ярославской и Новгородской областями. Тесными пространственными взаимовлияниями с окружающими регионами обладают также Республика Татарстан,

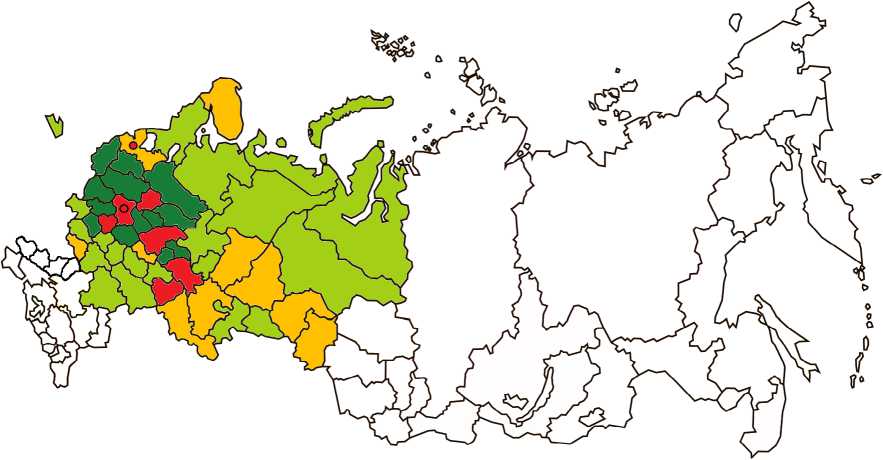
Пространственный кластер регионов с высоким объемом отгруженных инновационных товаров

Формирующийся пространственный кластер регионов с высоким объемом отгруженных инновационных товаров

Регионы, испытывающие сильное влияние полюсов роста и пространственных кластеров

Регионы, испытывающие слабое влияние полюсов роста и пространственных кластеров

Регионы с более низким объемом отгруженных инновационных товаров по сравнению с окружающими

территориями

Рис. Диаграмма рассеивания П. Морана по объему отгруженных инновационных товаров в регионах России в 2021 году

Источник: составлено авторами.

Таблица 2. Прямые и обратные пространственные взаимовлияния регионов по объему отгруженных инновационных товаров, выполненных работ и оказанных услуг в 2021 году

Инновационно активные регионы	Регионы, обладающие прямыми пространственными взаимовлияниями	Регионы, обладающие обратными пространственными взаимовлияниями
г. Москва	Республика Татарстан г. Санкт-Петербург Московская область Ярославская область	Владимирская область Ивановская область Калужская область Костромская область Рязанская область
г. Санкт-Петербург	Республика Татарстан Московская область Ярославская область	Новгородская область
Республика Татарстан	Самарская область Московская область Ярославская область	Чувашская Республика Республика Марий Эл
Ярославская область	Республика Татарстан Московская область	Ивановская область Костромская область
Источник: составлено авторами.

Ярославская область. Значительное влияние отмеченных выше регионов на окружающие территории подтверждает и диаграмма рассеивания П. Морана.

Регионы, формирующие квадрант LH диаграммы, окрашенные темным зеленым цветом, располагающиеся в окружении пространственного кластера регионов с высоким объемом отгруженных инновационных товаров, испытывают их сильное воздействие. В зону сильного влияния регионов, формирующих пространственный инновационный кластер, вошли Орловская, Рязанская, Смоленская, Владимирская, Ивановская, Калужская, Костромская, Вологодская, Тверская, Новгородская, Псковская области, а также республики Марий Эл и Чувашия, то есть центральные регионы России.

Не все регионы, формирующие квадрант HH диаграммы, обладают тесными пространственными взаимосвязями с территориальными системами, оказывают сильное влияние на окружающие регионы. В данном квадранте мы выделили регионы, обладающие потенциалом для формирования пространственного кластера (окрашены желтым цветом на диаграмме рассеивания П. Морана). К ним относятся Свердловская, Оренбургская, Ленинградская, Белгородская, Мурманская, Омская и Тюменская области, Пермский край, а также республики Башкортостан и Мордовия. Эти регионы отличаются умеренным уровнем инновационной активности предприятий (входят во вторую группу регионов с объемом отгруженных инновационных товаров чуть выше среднего уровня по России) и умеренным влиянием на окружающие территории. Развитие межрегиональных пространственных взаимосвязей данных регионов с окружающими их территориями позволит им в будущем сформировать пространственный инновационный кластер и значительно повысить эффективность и скорость генерации и внедрения новых технологий.

Установленный кластер инновационно развивающихся регионов (г. Москва и г. Санкт-Петербург, Московская, Нижегородская, Тульская, Ярославская и Самарская области, Республика Татарстан) и их межрегиональные взаимосвязи с окружающими регионами должны, по нашему мнению, стать приоритетом государственной поддержки при реализации Стратегии пространственного развития России, которая ориентирована на укрепление межрегиональных взаимосвязей регионов в различных сферах. Государственная поддержка в виде бюджетных инвестиций, льготного кредитования и налогообложения должна оказываться и регионам, формирующим потенциальный кластер инновационного развития (Свердловской, Оренбургской, Ленинградской, Белгородской, Мурманской, Омской и Тюменской областям, Пермскому краю, а также республикам Башкортостан и Мордовия). Становление нового кластера будет способствовать развитию и укреплению пространственных взаимосвязей с окружающими регионами, а это приведет в дальнейшем к формированию новых инновационных центров в России и повышению инновационной активности окружающих территорий.

Построенная в результате пространственного автокорреляционного анализа диаграмма Морана наглядно подтверждает пространственную неоднородность инновационного развития предприятий в России. Подавляющее большинство регионов, точнее почти вся восточная часть России, характеризуется низким уровнем инновационной активности предприятий, низким объемом отгруженных инновационных товаров, выполненных работ и оказанных услуг (окрашены белым цветом на диаграмме), отсут- ствием тесных пространственных взаимовлияний с другими регионами, отличающимися высокой инновационной активностью предприятий. И здесь, как мы предполагаем, негативное влияние оказывает значительная удаленность регионов от инновационных центров России.

Для оценки влияния факторов на инновационную активность предприятий, в частности на объем отгруженных в регионах инновационных товаров, выполненных работ и услуг нами были построены регрессионные модели, характеризующие производственную функцию Кобба – Дугласа. Данная функция предполагает оценку влияния двух ключевых факторов: объема затрат организаций на осуществление инновационной деятельности и численности персонала, занятого научными исследованиями и разработками. Перед построением регрессионных моделей была проведена оценка стационарности исходных данных, расчет и анализ описательных статистик. Их значения представлены в табл. 3.

Таблица 3. Описательные статистики переменных в модели, результаты оценки стационарности временных рядов

	V	C	L
Среднее	5,439	4,822	7,413
Медиана	6,252	5,519	7,602
Минимум	-8,082	-7,037	-6,738
Максимум	11,098	9,778	12,594
Стандартное отклонение	3,134	2,802	2,517
Вариация	58%	58%	34%
Асимметрия	-1,160	-1,161	-1,883
Эксцесс	1,034	1,073	6,431
5%-перцентиль	-1,077	-1,236	2,940
95%-перцентиль	9,329	8,241	10,542
Interquartile range	2,987	2,986	2,365
Внутригрупповое ст. отклонение	1,125	0,903	0,471
Межгрупповое отклонение	2,952	2,674	2,489
Im-Pesaran-Shin t-bar. (в скобках указано критическое значение при уровне надежности 95%)	-2,81 (-1,69)	-3,09 (-1,69)	-2,13 (-1,69)
Мета-тесты Choi:
– инверсный Хи-квадрат (170)	469,7***	561,3***	281,6***
– инверсный тест на нормальность	-12,8***	-15,1***	-6,2***
– логит тест: t (429)	-13,1***	-16,1***	-6,1***
Источник: составлено авторами.

Для оценки стационарности временных рядов использовался расширенный тест Дикки – Фуллера. В результате исследования нулевая гипотеза о существовании единичного корня в исходных данных по каждому региону и всем переменным в модели была отклонена и подтверждена стационарность данных. Рассчитанные описательные статистики подтвердили некоторую неоднородность исходных данных, наблюдается значительный уровень их вариации, присутствует асимметрия, однако следует отметить, что до извлечения натурального логарифма из исходных данных уровень их неоднородности был значительно выше. В ходе исследования были построены три стандартные регрессии: сквозная, объединенным (pooled) методом наименьших квадратов, с фиксированными и случайными эффектами (табл. 4).

Все три модели не прошли тестирование предпосылок МНК, в них наблюдается автокорреляция остатков, гетероскедастичность, кросс-секционная зависимость в панельных данных. Однако, если не принимать во внимание нарушение предпосылок МНК, лучшие результаты были установлены моделью с фиксированными эффектами. Она обладает наименьшими значениями информационных критериев Шварца и Акаике, стандартной ошибки модели, остаточной дисперсии, более высоким коэффициентом детерминации. Данная модель подтвердила значимость коэффициентов регрессии всех переменных и влияние рассматриваемых факторов. В отличие от моделей, построенных с использованием объединенного МНК и случайными эффектами, модель с фиксированными эффектами установила обратную зависимость объема отгруженных в регионах России инновационных товаров и численности персонала, занятого научными исследованиями и разработками, а также влияние других факторов, которые в модели не учитываются. Высокое значение константы свидетельствует о том, что на объем отгруженных товаров могут воздействовать и другие факторы.

Такими факторами, по нашему предположению, являются пространственные эффекты, возникающие от воздействия иннова-

Таблица 4. Результаты регрессионного анализа влияния различных факторов на динамику объема отгруженных предприятиями инновационных товаров, выполненных работ и оказанных услуг в регионах России за период с 2000 по 2021 год

Переменная	Модель по обобщенному ( pooled ) МНК	Модель с фиксированными эффектами	Модель со случайными эффектами
Const	-0,141 (0,18)	8,661 (0,82)***	-0,141 (0,18)
Ln ( C it )	0,832 (0,02)***	0,366 (0,03)***	0,832 (0,02)***
Ln ( L it )	0,215 (0,03)***	-0,579 (0,1)***	0,215 (0,03)***
R-squared	0,659	0,836
F-statistic	1659,4***	105,5***
S.E. of regression	1,449	1,029	1,449
Sum squared resid	3599,8	1734,9	3599,8
Schwarz criterion	6163	5484	6163
Akaike info criterion	6147	5048	6147
Durbin-Watson stat	0,724	1,146	1,838
White»s test for heteroskedasticity	130***	15323***
Test for normality of residual	240***	1073***	240***
Wooldridge test for autocorrelation	17,7***	64,3***	1,7***
Pesaran CD test	17,8***	12,5***	39,9***
Breusch-Pagan test statistic (LM)	2953,4***
Hausman test statistic (H)	138,8***
Источник: составлено авторами.

ционно развивающихся предприятий окружающих территориальных систем. Могут возникать и пространственные эффекты от воздействия рассматриваемых в модели факторов, сосредоточенных на территории соседних регионов. Их влияние было протестировано пространственной моделью Дарбина. Данная модель оценивает не только воздействие факторов определенной территории на результативный признак, но и определяет пространственный лаг воздействия результативного и факторных признаков окружающих территорий. При построении модели Дарбина использовались две матрицы пространственных весов: по смежным границам между регионами и линейным расстояниям между их административными центрами (табл. 5).

Используемые в моделировании матрицы пространственных весов позволили получить похожие результаты оценки параметров тестируемых переменных. Однако более высокое значение квадрата корреляции смоделированных и исходных значений по объему отгруженных инновационных товаров в регионах, более низкие значения остаточной дисперсии, стандартных ошибок модели и информационных критериев Шварца и Акаике свидетельствуют об оптимальности использования матрицы пространственных весов по смежным границам между регионами при формировании модели Дарбина.

Достоверность данной модели подтверждает Sargan – Hansen test (J-statistic), который проверяет нулевую гипотезу о корректности модели, о состоятельности параметров регрессии. Данная гипотеза принимается в модели. Достоверность построенной модели оценивалась и с помощью Arellano-Bond serial correlation test, который позволил подтвердить нулевую гипотезу об отсутствии автокорреляции возмущений второго порядка. Автокорреляция возмущений первого порядка в пространственных моделях допускается. Статистика Jarque-Bera подтвердила нормальность распределения слу-

Таблица 5. Пространственная модель Дарбина, отражающая зависимость динамики объема отгруженных предприятиями инновационных товаров, выполненных работ и оказанных услуг в регионах России от различных факторов (по двум матрицам пространственных весов)

	Матрица пространственных весов по линейным расстояниям	Матрица пространственных весов по смежным границам
Variable	Coefficient	Coefficient
Y (-1)	0,041 (0,003)***	0,035 (0,003)***
WV	0,928 (0,002)***	0,933 (0,004)***
WLn ( C it )	-2,256 (0,854)***	-6,104 (0,913)***
WLn ( L it )	32,251 (10,168)***	7,578 (2,848)***
Ln ( C it )	0,087 (0,007)***	0,113 (0,011)***
Ln ( L it )	-0,013 (0,060)	0,048 (0,034)
Квадрат корреляции ( V; V mod )	0,941	0,962
S.E. of regression	0,264	0,206
Sum squared resid	107,2	65,06
Sargan–Hansen test (J-statistic)	54,73	38,35
Prob ( J-statistic)	0,371	0,921
Jarque-Bera	3908114***	4898682***
Arellano-Bond Serial Correlation Test: AR(1) AR(2)	-11,71 (3,85)*** -3,34 (2,66)	-8,15 (2,48)*** -2,56 (2,03)
Durbin-Watson stat	2,23	2,24
Schwarz criterion	0,079	0,063
Akaike info criterion	-0,01	-0,026
Источник: составлено авторами.

чайных ошибок в модели. Более низкий уровень ошибок в пространственной модели Дарбина и близкое к нулю значение константы по сравнению со стандартными регрессионными моделями показали необходимость учета пространственных эффектов при моделировании динамики инновационной активности предприятий в регионах России. В условиях высокой неоднородности социально-экономического развития территорий различного уровня, которая отчетливо наблюдается в России, пространственные модели, учитывающие пространственный лаг переменных, позволяют более точно смоделировать исследуемые процессы.

Как и на предыдущем этапе исследования, модель Дарбина подтвердила отсутствие влияния численности научноисследовательских кадров в регионах на объем отгруженных инновационных товаров, выполненных работ и оказанных услуг. Численность научно-исследовательских кадров, как показали наши более ранние исследования, значительно влияет на динамику генерируемых в регионах передовых производственных технологий, а также выдаваемых патентов на изобретения и полезные модели. В процессах внедрения новых технологий и производства инновационной продукции научно-исследовательские кадры задействованы в меньшей степени, поэтому вполне закономерно, что модель не установила их влияние на динамику отгруженных инновационных товаров. В связи со сказанным приоритет государственной инновационной политики должен быть смещен в сторону поддержки регионов, уже обладающих научно-исследовательским потенциалом, для активного внедрения разрабатываемых передовых производственных технологий и нововведений, а не наращивания научно-исследовательского потенциала территорий.

Модель Дарбина выявила положительное влияние научно-исследовательских кадров, размещающихся в соседних регионах. Значительная часть научно-исследовательских кадров концентрируется в регионах первой и второй групп, выделенных нами по объему отгруженных инновационных товаров. Поэтому вполне закономерно, что в субъектах РФ с незначительной численностью научно-исследовательских кадров они не оказывают должного влияния на динамику инновационного развития предприятий и предприятия вынуждены привлекать специалистов из окружающих регионов. В результате окружающие территории с более высокой концентрацией научно-исследовательских кадров оказывают положительное воздействие на регионы, ими не обеспеченные. Пространственный эффект от воздействия окружающих субъектов РФ с высокой численностью научно-исследовательских кадров на динамику инновационного развития регионов России положительный и очень значительный. Таким образом, регионы, располагающиеся в окружении территорий с высокой концентрацией научно-исследовательских кадров (г. Москва и г. Санкт-Петербург, Республика Татарстан, Нижегородская область и др.), получают значительное преимущество перед удаленными регионами в использовании научно-исследовательских кадров для осуществления предприятиями инновационной деятельности. Именно поэтому при разработке и реализации государственной политики инновационного развития отдельное внимание должно быть уделено формированию механизмов развития межрегиональных взаимосвязей, чтобы удаленные от инновационных центров регионы могли перенимать опыт внедрения нововведений и развиваться инновационно, имели доступ к научной и инновационной инфраструктуре. Необходимо формировать тесные взаимосвязи удаленных территорий с научноисследовательскими центрами для переподготовки кадров, повышения уровня квалификации работников.

Пространственный автокорреляционный анализ по методике П. Морана подтверждает данный вывод: регионы, располагающиеся в центральной части России в окружении г. Москвы, г. Санкт-Петербурга и других регионов, формирующих пространственный инновационный кластер, испытыва- ют очень сильное их влияние и отличаются более высоким уровнем инновационной активности, чем удаленные субъекты.

Пространственная модель Дарбина показала, что основным фактором инновационного развития территорий являются инвестиции, в частности затраты предприятий на инновационную деятельность. Однако, в отличие от других исследований, нами было установлено, что инвестиции положительно влияют только на инновационное развитие субъектов РФ с высоким уровнем их концентрации, с развитым научно-исследовательским потенциалом, то есть на центральные регионы, формирующие пространственный кластер, представленный на рисунке. Окружающие их регионы испытывают отрицательное влияние осуществляемых предприятиями затрат на инновационную деятельность. Возможно, отсутствие мощного научно-исследовательского потенциала на таких территориях, способности генерировать новые производственные технологии приводит к низкой эффективности осуществляемых предприятиями инвестиций. Высокая концентрация направляемых на инновационную деятельность финансовых ресурсов в центральной части России подтверждает вывод, полученный в ходе моделирования, поэтому для активного инновационного развития регионов необходимо формирование новых механизмов привлечения инвестиций, льготного банковского кредитования. Однако такие механизмы не будут эффективными без государственной поддержки формирования и укрепления межрегиональных, кооперационных взаимосвязей в научной и инновационной сферах.

Заключение

В ходе исследования была проведена оценка пространственных особенностей инновационного развития регионов России и построена модель Дарбина для определения пространственных эффектов, возникающих в результате воздействия окружающих территорий. Модель Дарбина установила положительное влияние выделяемых предприятиями внутри региона финансовых ресурсов на инновационную деятельность, на динамику объема отгруженных инновационных товаров и в то же время негативное их воздействие на динамику отгруженных инновационных товаров в соседних регионах. Высокий уровень концентрации финансовых ресурсов, выделяемых на инновационную деятельность, в определенных регионах (первой и второй групп по объему отгруженных инновационных товаров) способствует активному инновационному развитию функционирующих на этих территориях предприятий. В результате регионы, менее обеспеченные финансовыми ресурсами и располагающиеся в непосредственной близости к ведущим инновационным центрам, отличаются более низкой инновационной активностью предприятий, объем отгруженной ими инновационной продукции снижается. Они получают преимущество в плане доступа к научно-исследовательским кадрам, научной инфраструктуре инновационных центров и в то же время испытывают негативное влияние центров из-за возможного оттока финансов для оплаты ресурсов в целях осуществления инновационной деятельности, которыми не обеспечены.