Моделирование ПЗС-формирователя сигналов изображений со сверхразрешением

Размеры фоточувствительных элементов (пикселей) современных матриц ПЗС или КМОП достигли значений в районе 4–6 мкм [3; 11]. Возникает вопрос, почему нельзя еще больше уменьшить размер пикселя, если сегодня можно изготовить элементы кремниевых микросхем с размерами меньше десятых долей микрометра. Ответ на этот вопрос связан с глубиной проникновения фотонов в кремний, показанной на рисунке 1 для видимого диапазона длин волн. Глубина проникновения фотонов зависит от степени легирования кремния, поэтому здесь приведена грубая оценка глубины проникновения, ясно показывающая стремительный рост этой величины с приближением к инфракрасному диапазону длин волн.

Генерируемые на большой глубине носители заряда (электроны или дырки), диффундируя к поверхности полупроводника, отклоняются от места входа в полупроводник порождающего их фотона, тем самым приводя к размытию сигналов изображения. Для предотвращения этого нежелательного эффекта приходится перед фоточувствительной матрицей ставить светофильтр, отрезающий инфракрасную часть спектра.

Выпуск 4/2019

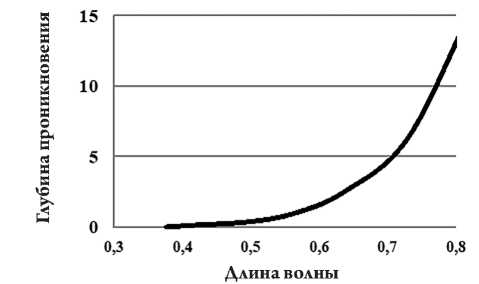
Рис.1. Приблизительная оценка зависимости глубины проникновения фотонов в кремний от их длины волны в видимом диапазоне длин волн, мкм

При уменьшении размера пикселя ниже 5 мкм возникает необходимость отрезать не только инфракрасную, но и красную часть спектра, уменьшая тем самым чувствительность формирователя сигналов изображения в видимом диапазоне спектра. Еще острее данная проблема предстает в инфракрасном диапазоне, где глубина проникновения фотонов в кремний превышает 15 мкм.

С этим явлением столкнулись в 1993 г. сотрудники компании Samsung, разрабатывавшие промышленный робот для сборки интегральных схем. В качестве осветителя они планировали использовать светодиоды инфракрасного диапазона и обнаружили, что высокоразрешающая японская камера в этом диапазоне имела чувствительность на два порядка хуже чувствительности скромной российской камеры. За советом они обратились к автору данной статьи, который разъяснил им, что японская камера содержала светофильтр, отрезающий инфракрасную часть спектра, а российская камера при большом размере пикселя в таком фильтре не нуждалась.

В связи с этим ограничением на уменьшение размера пикселя фоточувствительной матрицы приходится искать альтернативные способы повышения разрешающей способности формирователей сигналов изображений (ФСИ) при сохранении размеров пикселя. Одним из таких способов может быть синтез изображения с использованием алгоритмов сверхразрешения [1; 12]. Это направление повышения качества изображений привлекает в последние годы большое внимание исследователей.

Широко применяемые в настоящее время матрицы приборов с зарядовой связью (ПЗС) с синхронным накоплением энергии движущихся изображений [2; 7] для наблюдения поверхности Земли из космоса [5; 8], называемые также матрицами с временной задержкой и накоплением (ВЗН) [10], способны обеспечить эффект сверхразрешения за счет суперпозиции сигналов изображений от разных секций матрицы [4]. Стоит заметить, что понятие «временная задержка и накопление» не отражает основную особенность работы этих матриц, а именно синхронизацию продвижения зарядов с движением изображения. Это особенно важно при формировании синтезированного потока цифровой информации, соответствующего суперпозиции сигналов от отдельных секций сложной матрицы.

На рисунке 2 показан фрагмент двухсекционной матрицы, обеспечивающей при синхронном с движением изображения переносе зарядов совмещение перекрестий столбцов и строк первой секции с центрами пикселей второй секции.

Седунов Б.И. Моделирование ПЗС-формирователя сигналов изображений...   25

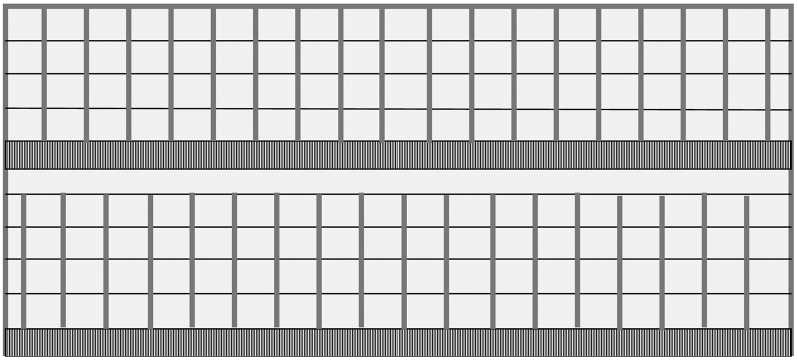
Рис. 2. Фрагмент двухсекционной матрицы с синхронным переносом зарядов со сдвигом на половину пикселя сигналов строк и столбцов, сформированных первой секцией, относительно выхода второй секции

Два выходных регистра такой матрицы выдают сдвинутые на половины периодов по строке и столбцу сигналы. Эти сигналы можно передать на наземный пункт в виде двух независимых потоков, а на Земле осуществить суперпозицию данных потоков в цифровом комплексе наземной обработки сигналов изображений [9].

В настоящей статье проводится компьютерное моделирование ФСИ отдельных секций двухсекционной матрицы, моделирование синтеза совмещенного изображения от двух секций и сравнение качества синтезированного изображения с качеством изображения, формируемого одиночной секцией.

Программа моделирования освещенности ПЗС позволяет варьировать угол наклона и ширину шпал миры. В качестве тестового используется синусоидальное распределение яркости штриховой миры при различных углах наклона шпал миры (рис. 3). Синусоидальный закон распределения яркости тестового сигнала выбран для обеспечения возможности сравнения результатов моделирования с аналитическими оценками средних величин функции передачи модуляции (ФПМ) [6]. Ввиду малости шага поля освещенности численные значения на рисунке 3 округлены до одного знака (0 или 1), поэтому не отражают плавного изменения освещенности.

Рис. 3. Фрагмент поля распределения освещенности матрицы ПЗС для синусоидальной миры с наклоном шпал в 30° по отношению к строке и с шириной шпалы в 0,8 от размера пикселя. Шаг поля освещенности в 10 раз меньше размера пикселя

26 в ыпуск 4/2019

На рисунке 3 показан фрагмент одной строки матрицы ПЗС, состоящий из двух пикселей, освещенных через штриховую миру с углом наклона шпал в 30° относительно строк матрицы и с шириной шпал миры в 0,8 от размера пикселя. Заметим, что алиасинг катастрофически портит сигналы изображения, формируемые отдельными секциями при ширине шпал миры меньше размера пикселя [6].

Для повышения точности вычисления заряда, сгенерированного в отдельном пикселе, каждый пиксель разделен на 10×10 квадратов со своей собственной освещенностью. Центры пикселей двух секций сдвинуты на 5 шагов по вертикали и горизонтали. Этот сдвиг существенно снижает влияние алиасинга [Там же] на качество синтезированного изображения. Одна из целей статьи – оценить минимально допустимое отношение ширины шпалы к размеру пикселя для синтезированного изображения.

Программа компьютерного моделирования и анализа эффекта сверхразрешения в двухсекционной матрице ПЗС содержит две подпрограммы:

• •    Подпрограмма генерации распределения зарядов в одиночной секции или в двухсекционной матрице при различных углах наклона и ширины шпал миры.

• •    Подпрограмма анализа среднего и минимального локального значений ФПМ при заданных углах наклона и ширины шпал миры как для одиночной секции, так и для двухсекционной матрицы.

Моделирование распределения зарядов в матрице ПЗС

Синусоидальное распределение освещенности миры I ( x , y ) по поверхности матрицы ПЗС с углом наклона α (в радианах) и отношением δ ширины шпалы Δ _м к размеру пикселя Δ _п имеет вид

I ( x , y ) = (1 + sin(( y sin α – x cos α )π / δ)) / 2. (1)

Задавая различные значения α и δ , получаем все возможные виды синусоидального распределения освещенности матрицы ПЗС. Как сказано во введении, поле яркости изображения шпал миры дается с шагами, в 10 раз меньшими размеров пикселя по вертикали и горизонтали. Это обеспечивает плавное распределение освещенности по поверхности каждого пикселя.

Дискретное распределение зарядов по пикселям Z(i, j) получаем интегрированием распределения освещенности по площади каждого пикселя секции матрицы. На рисун-

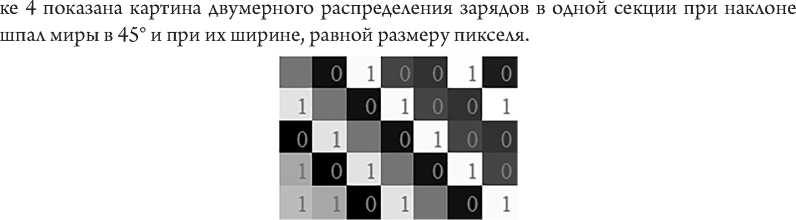
Рис. 4. Фрагмент поля распределения зарядов в матрице ПЗС при угле в 45° и при δ = 1

Указанные в квадратиках значения не отражают плавного характера изменения зарядов пикселей из-за грубого округления, но это плавное изменение хорошо видно на рисунке 5, где показано распределение зарядов пикселей вдоль одного из столбцов.

Седунов Б.И. Моделирование ПЗС-формирователя сигналов изображений...    27

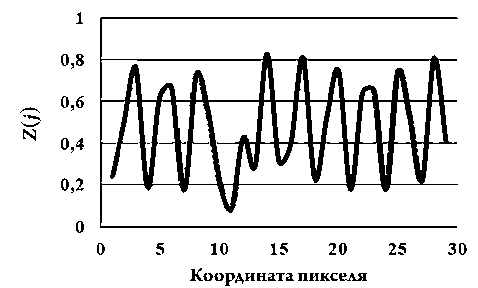
Рис. 5. Распределение зарядов вдоль одного из столбцов матрицы (см. рис. 4)

Рисунок 5 показывает, что при ширине шпалы миры, равной размеру пикселя, локальный контраст зарядового поля крайне неоднороден и в районе 12-й строки локальный контраст C_loc становится недопустимо малым. В этом проявляется алиасинг [6]. Под локальным контрастом понимаем отношение разности величин соседних максимума и минимума сигнала к их сумме: C_loc = ( Z_max – Z_min ) / ( Z_max + Z_min ).

Анализ функций передачи модуляции в матрицах ПЗС

Переносим вычисленные Z ( i , j ) во фрагмент секции с выбранными числами пикселей в строке N_r и в столбце N_c . Выбранные нами числа N_r = 7 и N_c = 29 дают средние значения ФПМ с достаточной точностью, без перегрузки компьютера излишними вычислениями. Создаем ряд таблиц с размерностью N_r × N_c и заносим в них значения по формуле

A_ijn = ЕСЛИ((( y_j – 0,5) – ( x_i – 0,5) / tg( α ) – Y_n )²< 0,25; 1; 0). (2)

Эта формула расставляет единицы вдоль прямой линии, параллельной штрихам миры, сдвинутой по вертикали на значение Y_n . Меняя целочисленные значения Y_n от нуля до Y_n max , получаем набор таблиц со сдвигом линии единиц. Ввиду дискретности матрицы эта линия получается ломаной. Суммируя значения A_ijn по горизонтали и затем по вертикали, получаем полное число ячеек таблицы, отмеченных значением «1».

Создаем второй набор таблиц значений B_ijn , соответствующих величинам зарядов в отмеченных значением «1» пикселях матрицы:

B_ijn = A_ijnZ ( i , j ). (3)

Суммируя значения B_ijn по горизонтали и затем по вертикали, получаем полную сумму зарядов пикселей вдоль ломаной линии, отмеченной значением «1». Деля эту сумму на найденное число отмеченных ячеек, получаем значение среднего заряда Z_n вдоль линии с начальной координатой по вертикали, равной Y_n . Строим два вертикальных столбца для Y_n и Z_n . Зависимость Z_n ( Y_n ) показана на рисунке 6 для угла наклона шпал в 30° и их ширины, равной размеру пикселя.

Рисунок 6 показывает, что при δ = 1 в секции матрицы наблюдается большая неоднородность среднего заряда пикселя. Для качественного распознавания изображений шпал миры требуется, чтобы их локальный контраст превышал некое установленное значение.

28 в ыпуск 4/2019

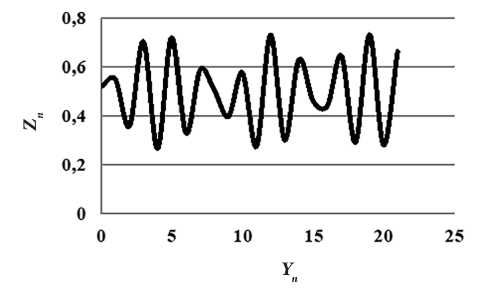
Рис. 6. Зависимость средней величины заряда пикселя Z_n вдоль прямой, параллельной направлению штрихов миры, от величины сдвига Y_n начала этой прямой по вертикали.

Угол наклона штрихов миры равен 30°, а ширина миры равна размеру пикселя

Для нахождения минимальных и средних значений локального контраста сначала отмечаем значения n , соответствующие локальным максимуму и минимуму Z_n :

I ( Z_max ) = ЕСЛИ(И( Z_n >  Z_{n – 1} ; Z_n >  Z_{n + 1} ); 1; 0), I ( Z_min ) = ЕСЛИ(И( Z_n <  Z_{n – 1} ; Z_n <  Z_{n + 1} ); 1; 0).

Затем строим столбцы продолженных значений Z_{max n} и Z_{min n} по формулам

Z_{max n} = ЕСЛИ( I ( Z_max ) = 1; Z_n ; Z_{max n – 1} ), Z_{min n} = ЕСЛИ( I ( Z_min ) = 1; Z_n ; Z_{min n – 1} ).

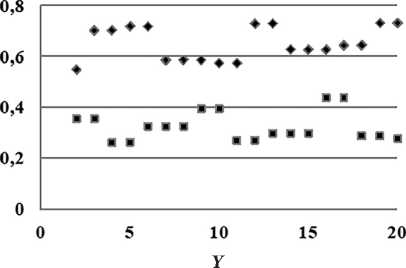
Продолженные значения Z_{max n} и Z_{min n} не ограничены локальными максимумами или минимумами, но продолжаются до появления нового локального максимума или минимума (рис. 7).

Е

N s

N

n

Рис. 7. Продолженные значения локальных максимумов (ромбы) и локальных минимумов (квадраты) при наклоне шпал в 30° и δ = 1

ФПМ матрицы равна коэффициенту передачи контраста при использовании синусоидальной миры. Переход от просто локальных максимумов и минимумов к продолженным позволяет получить для одного значения Y_n оба значения Z_{max n} и Z_{min n} , что обеспечивает вычисление локального контраста:

Седунов Б.И. Моделирование ПЗС-формирователя сигналов изображений...    29

loc max n min n         max n min n .

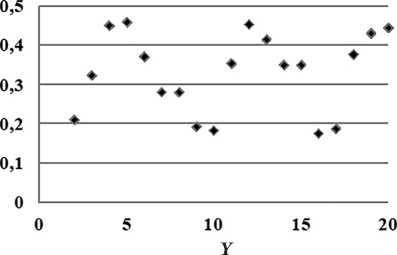
На рисунке 8 показаны изменения локального контраста C_loc с номером Y_n линии, параллельной шпалам миры.

n

Рис. 8. Большая неоднородность локального контраста сигналов изображения при наклоне шпал синусоидальной миры в 30° и ширине шпал, равной размеру пикселя

Для качественного распознавания изображения важно иметь достаточно большую величину минимального контраста и малый разброс значений локального контраста. Этому требованию соответствует критерий: разность удвоенного минимального локального контраста и среднего значения контраста должна быть больше 0,2. Для проверки выполнимости данного критерия при фиксированных условиях моделирования α и δ вычисляем минимальное и среднее значения контраста сигнала изображения и на этой базе оцениваем значение критерия разрешения (рис. 9).

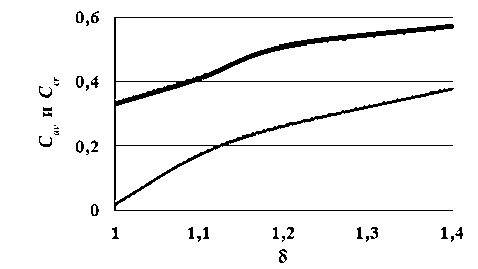
Рис. 9. Средний коэффициент передачи контраста C_av (толстая линия) и критерий качества передачи контраста C_cr (тонкая линия) в зависимости от относительной ширины шпалы миры δ при наклоне шпал синусоидальной миры в 30°

Повторяя описанную процедуру для различных углов наклона шпал миры, найдем минимально допустимое значение δ , удовлетворяющее сформулированному ранее критерию. Для одиночной секции матрицы ПЗС это значение равно 1,12.

Анализ ФПМ синтезированной виртуальной матрицы

Суперпозиция зарядовых полей от двух секций матрицы ПЗС снижает вклад алиасинга в неоднородность локального контраста синтезированного зарядового поля.

30 в ыпуск 4/2019

При этом начальные координаты пикселей второй секции сдвинуты относительно начальных координат x_i и y_j пикселей первой секции на 0,5 по x и y .

Мы присваиваем вычисленные значения Z ( i , j ) для перекрывающихся пикселей двух секций неперекрывающимся субпикселям в 2 раза меньшего размера, показанным на рисунке 10 в виде малых темных квадратов. Но число субпикселей в виртуальной матрице в 4 раза превышает число пикселей в одной секции. Поэтому такая виртуальная матрица имеет пробелы между субпикселями по вертикали и горизонтали.

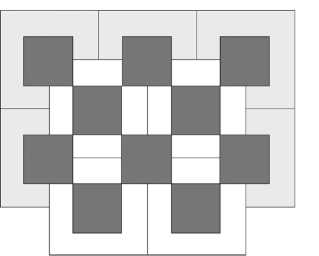
Рис. 10. Формирование виртуальной матрицы высокого разрешения из двух секций:

1) фрагмент первой секции из 6 пикселей с серым обрамлением; 2) фрагмент второй секции из 4 пикселей с белым обрамлением, совмещенной с первой секцией со сдвигом на половину размера пикселя по горизонтали и вертикали; 3) 10 темных субпикселей, которым присвоены величины зарядов Z ( i , j ) тех пикселей, в центре которых они находятся; 4) белые субпиксели, которым присвоен заряд, равный среднему арифметическому от четырех ближайших к ним темных субпикселей

Итак, синтезированное распределение зарядов в виртуальной матрице со сверхразрешением имеет в 2 раза меньший шаг, нежели размер пикселя. Тем самым мы приходим к виртуальным субпикселям, которым приписываем вычисленные ранее значения зарядов Z ( i , j ). А для промежуточных субпикселей мы приписываем средние значения от зарядов Z ( i , j ) ближайших субпикселей по вертикали и горизонтали. Так как среднее значение меньше максимального значения и больше минимального значения усредняемых зарядов Z ( i , j ), процедура усреднения не влияет на величину локального контраста распределения зарядов, но сглаживает результирующее поле зарядов.

На рисунке 11 показано синтезированное поле распределения зарядов при тех же условиях освещения двухсекционной матрицы, что и на рисунке 4, а на рисунке 12 показано распределение зарядов вдоль одного из столбцов виртуальной матрицы.

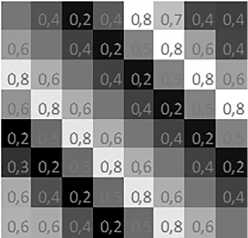
Рис. 11. Синтезированное поле зарядов в виртуальной матрице при α = 1 и при δ = 1

Седунов Б.И. Моделирование ПЗС-формирователя сигналов изображений...    31

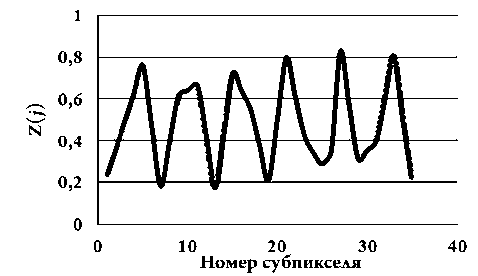
Рис. 12. Распределение зарядов вдоль одного из столбцов виртуальной матрицы (см. рис. 11)

Рисунок 12 показывает, что однородность локального контраста в виртуальной матрице существенно выше, чем в исходной секции при одинаковых условиях освещения матриц. Но сверхразрешение синтезированных виртуальных матриц можно оценить только в результате детального анализа распределения зарядовых полей.

Как показано в работе [6], среднее значение ФПМ матрицы ПЗС равно

C_av = (sin(π / 2δ) / (π / 2δ))². (9)

Синтезированная виртуальная матрица обеспечивает лучшее приближение сигнала изображения к синусоидальной форме, поэтому ее ФПМ прекрасно соответствует формуле (9) (рис. 13).

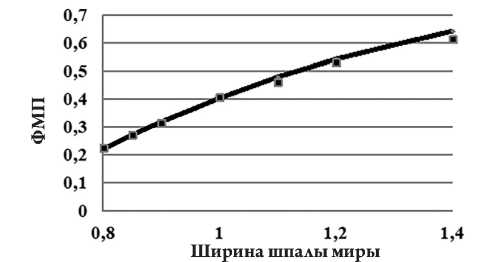
Рис. 13. Функция передачи модуляции матрицы ПЗС со сверхразрешением в зависимости от отношения ширины шпалы к размеру пикселя: сплошная линия – теория; маркеры – результат моделирования при отклонении шпал миры от строк матрицы на 15°

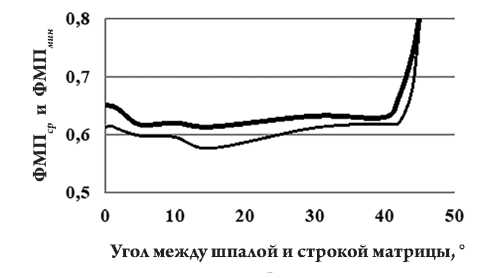
Для углов наклона шпал миры в 15 и 30° ФПМ почти одинакова (рис. 14), но при некоторых углах наблюдаются резонансные всплески средних значений ФПМ (рис. 15).

Рисунок 15 показывает, что среднее значение ФПМ почти не меняется в диапазоне углов наклона шпал миры по отношению к строкам матрицы ПЗС от 3 до 40°, что соответствует данным на рисунке 14. Но при 0 и 45° наблюдаются всплески, аналогичные максимумам функции рассеяния рентгеновского излучения на кристаллической решетке. Однако эти всплески не слишком меняют среднюю по углам величину ФПМ и не ухудшают ее соответствия формуле (9).

Выпуск 4/2019

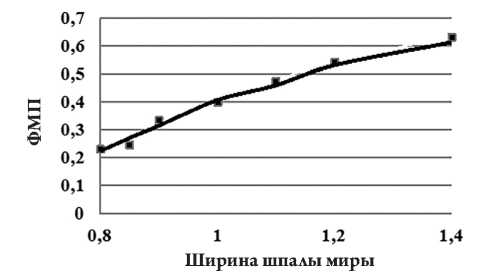
Рис. 14. Независимость ФПМ от угла наклона шпал миры по отношению к строкам матрицы ПЗС: сплошная линия – угол равен 15°; маркеры – угол равен 30°

Угол между шпалой и строкой матрицы, °

Рис. 15. Резонансные всплески значений ФПМ при ширине шпалы миры, равной 1,4 размера пикселя, и при углах наклона шпалы миры по отношению к строке матрицы, равных 0 и 45°: толстая линия – средние значения ФПМ; тонкая линия – минимальные значения ФПМ

Рисунок 15 также показывает, что в синтезированной матрице различие между средним и минимальным локальным коэффициентом передачи контраста не столь велико, как в одиночной секции матрицы, что выражается в малом отличии критерия разрешения от величины средней ФПМ для синтезированной виртуальной матрицы (рис. 16).

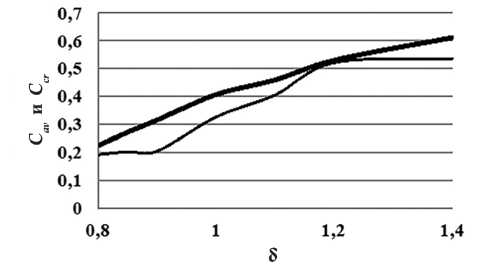
Рис. 16. Средний коэффициент передачи контраста C_av (толстая линия) и критерий качества передачи контраста C_cr (тонкая линия) в зависимости от относительной ширины шпалы миры δ при наклоне шпал синусоидальной миры в 15°

Седунов Б.И. Моделирование ПЗС-формирователя сигналов изображений...    33

Заключение

Таким образом, синтезированная виртуальная матрица с синхронным накоплением энергии движущегося изображения обеспечивает повышенное на 25% разрешение по сравнению с одиночной матрицей ПЗС.