Моделирование рабочих процессов, происходящих во фрикционных элементах управления гидромеханических трансмиссий тракторов

Для разработки высокоэффективных и информативных методов диагностирования фрикционных элементов управления гидромеханических трансмиссий тракторов возникает необходимость математического моделирования рабочих процессов, происходящих в них. Существующие математические модели процессов наполнения и опорожнения исполнительных цилиндров фрикционов разработаны для решения конструкторских задач и не учитывают влияния эксплуатационных факторов, влияющих на их работоспособность, а также инерционность подвижных элементов узла. Для разработки метода диагностирования потребовалось создание математической модели рабочих процессов фрикционных устройств, учитывающей силы инерции поршня исполнительного цилиндра, и эксплуатационныеизме-нения фрикционных дисков.

За объект моделирования взят фрикцион гидромеханической передачи трактора К-700А, так как в агропромышленном комплексе нашей страны тракторы семейства «Кировец» являются наиболее распространенными энергонасыщенными.

Для изменения скорости передвижения тракторов семейства «Кировец» в коробке перемены передач на ведущем валу установлены четыре фрикциона, которые представляют собой многодисковые муфты сцепления для каждой передачи. Сжатие пакета дисков осуществляется нажимным диском, который перемещается давлением масла, нагнетаемым через центральное отверстие вала насосом коробки передач. У новой конструкции ведущего вала, устанавливаемого в коробке передач тракторов К-700А, К-701, К-702, каждый фрикцион имеет 5 ведущих и 6 ведомых дисков – для 2-, 3- и 4-й передач и 6 ведущих и 7 ведомых дисков – для 1-й передачи. Общая высота собранных пакетов составляет соответственно 35,2…37,0 мм и 40,3…44,8 мм.

По статистическим данным надежность тракторов семейства «Кировец» во многом зависит от надежности гидромеханической коробки передач, на долю которых приходится более 55% отказов, при этом до 80% нарушение работоспособности гидромеханической передачи вызвано отказом фрикционов вследствие износа и нарушения пространственной геометрии фрикционных дисков, причем подавляющее большинство дисков имеют тарельчатое коробление.

Для разработки математической модели рабочих процессов, происходящих во фрикционах, составлена расчетная схема, приведенная на рисунке 1.

При составлении математической модели приняты следующие допущения:

• 1)    рабочая жидкость несжимаема;

• 2)    подводящие магистрали абсолютно жесткие;

• 3)    отсутствуют утечки рабочей жидкости из цилиндра и из магистрали подвода к нему;

• 4)    режим движения жидкости в магистралях турбулентный.

  

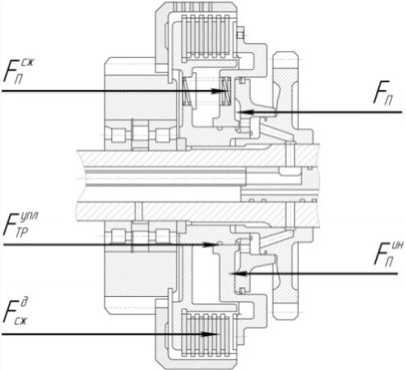
  Рис. 1. Расчетная схема фрикциона трактора «Кировец»

  
  

Описание динамики перемещения поршня исполнительного цилиндра с учетом представленных сил и их особенностей производилось с применением дифференциальных уравнений второго порядка, составленных по принципу Даламбера:

ин F_П

П

1 П сж

упл д

ТР    F сж

F ин где ^П

– сила инерции поршня;

FП – сила давления рабочей жидкости на поршень цилиндра; П сж – сила сжатия отжимных пружин поршня;

^ТР – сила трения в уплотнениях поршня;

д

^Fсж – сила, затрачивающаяся на сжатие коробленых дисков фрикциона, как ведущих, так и ведомых.

Силы, входящие в уравнение (1), определяются по следующим формулам:

d 2 x dt ²

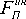
= m n

F n   p n S n

^Fcx = ^Fcx ₀ + ^СОП z On^X

F P = P n f m-p XP ( Г П - k m ) ²

В процессе эксплуатации диски фрикционов испытывают большие термодинамические нагрузки. В периоды трогания с места нагруженного трактора, а также при переключении передач поверхности трения ведущих и ведомых дисков интенсивно пробуксовывают, что приводит к их мгновенному разогреву.

Последующее охлаждение омываемым от насоса маслом вызывает тепловые удары. Так как ско- рости скольжения и нагрузки у наружных диаметров дисков выше, чем у внутренних, то и нагрев дисков, и пластические деформации у наружных диаметров гораздо больше, чем у внутренних. Это приводит к появлению тарельчатой деформации дисков.

Появление тарельчатой деформации приводит к следующим отрицательным явлениям в работе трактора:

– затрудняется переключение скорости движения трактора;

– трактор «ведет» при всех выключенных передачах;

– происходит спекание дисков пакета, что исключает возможность остановки трактора без оста- новки двигателя.

Для математического описания эксплуатационных изменений фрикционных дисков, выраженных в форме тарельчатой деформации, можно воспользоваться выражением для тарельчатых пружин:

F =

4 Ex

( 1 — Ц ² ) YD 1

где F – усилие сжатия тарельчатой пружины;

x – деформация пружины;

s – максимальная деформация;

b – толщина пружины;

D ₁ – наружный диаметр пружины;

D ₂ – внутренний диаметр пружины;

Е – модуль упругости II рода;

• и - коэффициент Пуассона.

Y -    6  (A-1 12; A - Da п ln (A)( A J      D2

Движение масла осуществляется в основном под давлением, создаваемым насосами, по трубопро- водам и каналам относительно малого диаметра, что позволяет использовать для его описания одномерные модели.

Одной из причин диссипации импульса является трение жидкости о стенки канала. Его величину принято оценивать в потерях давления по зависимости:

x . L . V

^A P ^{- (} p i — P 2 ) ^- ^ . Y . —— di . ² g

где λ – коэффициент потерь на трение жидкости;

• γ – удельный вес жидкости;

• L – длина канала;

• d l – гидравлический диаметр канала

• V – скорость жидкости.

При движении по масляному тракту потоку приходится преодолевать различные сопротивления, которые вызывают деформации потока и изменения его скорости. Потери импульса, вызванные этими сопротивлениями, носят название местных гидравлических потерь и оцениваются в величине потери давления по зависимости

Ap - £.у.V2/2g

где ξ – коэффициент местного сопротивления.

Величины λ,ξ берутся по справочным данным.

Уравнение неразрывности потока жидкости запишется в виде:

Fn . — - V. Fk - const, Пdt k

где F_П – площадь поршня исполнительного цилиндра;

dx

– скорость поршня исполнительного цилиндра;

dt

F_k – площадь сечения канала.

С помощью уравнений вида (2, 3) можно описать любой участок масляного тракта и, накладывая условия связи между участками (равенство давлений и неразрывность потока), получить модель гидравлического тракта в целом.

Представленная математическая модель позволяет расчетными методами получить зависимость изменения давления жидкости в исполнительном цилиндре во время включения фрикциона, учитывая при этом изменение параметров его технического состояния.

Решение уравнений гидравлики и динамики перемещения поршня исполнительного цилиндра производилось в среде MatLab, методом численного интегрирования Рунге-Кутта.

Для проверки математической модели было произведено измерение давления в гидроприводе управления фрикционами во время переключения передач при помощи экспериментальной установки, разработанной и изготовленной на кафедре «Автомобили» ВСГУТУ. Для вывода данных, идущих с датчика, разработана программа «Cursor Grapher». Программа позволяет отображать как весь график эксперимента, так и необходимую его область с автоматической настройкой масштаба. Также все данные и графики можно сохранять на ПК в форматах: «csv», для самой программы CursorGrapher, «jpg» графическое отображение и «xls» сохранение графиков в числовых значениях, для последующих вычислений и анализа данных.

На рисунке 2 представлены графики экспериментальных и расчетных исследований изменения давления в исполнительном цилиндре для фрикционов, не имеющих эксплуатационных изменений, и для фрикционов, имеющих тарельчатое коробление.

Анализ этих графиков подтверждает адекватность разработанной математической модели.

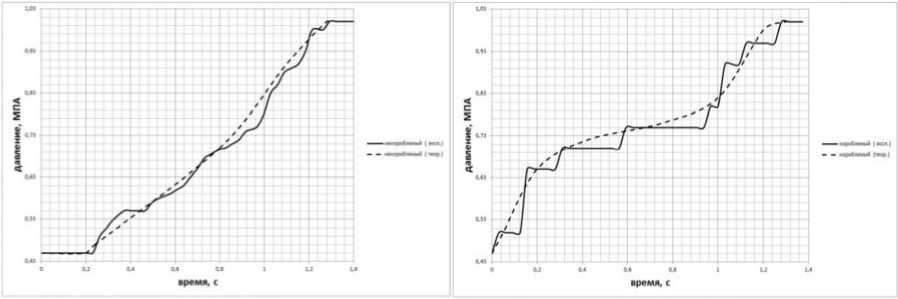
а                                              б

Рис.2. Графики изменения давления в исполнительном цилиндре фрикциона по времени: а – фрикционные диски без коробления; б – фрикционные диски, имеющие тарельчатые коробления