Моделирование работы двухчастотной системы посадки самолетов

Основным средством обеспечения инструментального захода самолетов гражданской авиации на посадку и посадки являются радиомаячные системы (РМС) посадки метрового диапазона длин волн формата ILS (Instrument Landing System). Проблема посадки самолетов в условиях ограниченной видимости взлетно-посадочной полосы (ВПП) возникла уже вскоре после первого полета братьев Райт в 1903 г. C изобретением в 1905 г. А.С. Поповым радио появились технические предложения по использованию электромагнитных волн для решения проблемы задания в пространстве радиотехнической траектории захода самолета на посадку. Таким образом, радиотехнические системы посадки (СП) имеют почти вековую историю развития. История развития СП в США описана в [1]. Основные вехи развития СП в нашей стране освещены в [2]. Радиомаяч-ная СП включает в себя (рис. 1) курсовой радиомаяк (КРМ), глиссадный радиомаяк (ГРМ), бортовую аппаратуру (БА) (на рис. 1 не показана).

КРМ установлен на продолжении оси взлетно-посадочной полосы (ВПП), на стороне, противоположной стороне захода самолета на посадку. Антенна КРМ излучает в окружающее пространство электромагнитные волны в диапазоне частот 108–112 МГц, модулированные по амплитуде сигналами тональных частот f ₁ = 90 Гц, f ₂ = 150 Гц. В идеальном случае поверхность, на которой разность глубин модуляции (РГМ) сигналами f ₁ и f ₂ равна нулю, представляет собой вертикальную плоскость, проходящую через ось ВПП (плоскость курса).

ГРМ установлен на расстоянии примерно 300 м от торца ВПП со стороны захода самолета на посадку и смещен от оси на некоторое расстояние. Антенна ГРМ излучает в окружающее пространство электромагнитные волны в диапазоне частот 328–332 МГц, модулированные сигналами с частотами f ₁ и f ₂ . Поверхность, на которой разность глубин модуляции сигналами f ₁ и f ₂

равна нулю, представляет собой конус, вершина которого находится в основании антенн, ось конуса вертикальна, а образующая наклонена на заданный угол относительно поверхности Земли (поверхность глиссады). Пересечение указанных поверхностей задает в пространстве радиотехническую траекторию для захода самолета на посадку, называемую глиссадой. Бортовая аппаратура индицирует отклонения самолета от глиссады, ее показания используются для принятия решения пилотом или автопилотом о корректировке траектории полета самолета.

Рис. 1. Схема размещения радиомаячной системы посадки

В процессе эксплуатации первых радиомаячных систем СП была обнаружена связь между точностными характеристиками СП и расположением и размерами местных предметов на аэродроме, таких как здание аэровокзала, ангары, стоянки самолетов и др., а также формой рельефа местности в зоне захода самолетов на посадку. Причиной искривлений глиссады являлась интерференция в области глиссады электромагнитных волн, отраженных от складок местности и от местных предметов, с электромагнитными волнами, формирующими глиссаду. Следует отметить, что проблема влияния волн, отраженных от окружающей местности, существует для всех радиотехнических угломерных навигационных систем. Однако эта проблема для СП является критической. Это обусловлено высокими требованиями к точности ILS, которые на порядок превышают таковые к аэродромным навигационным и радиолокационным системам.

Естественным стремлением разработчиков РМС было сужение диаграмм направленности антенны КРМ в горизонтальной плоскости, при которой местные предметы не облучались бы сигналами КРМ [2]. Применительно к ГРМ предлагались антенные решетки с низким уровнем облучения складок местности. Однако, при этом существенно сужается зона действия СП. Пилоту трудно попасть в узкую зону. Международной организацией гражданской авиации установлены минимальные угловые размеры зоны действия системы ILS [3]: ±35° в азимутальной плоскости для КРМ и примерно от 1 до 5,5° в угломестной плоскости для ГРМ.

Проблема обеспечения, с одной стороны, высокой точности задания траектории полета путем сужения ДН антенн и, с другой стороны, широких зон действия КРМ и ГРМ была решена в радиомаяках с двухчастотным режимом работы. При этом используется так называемый эффект захвата (capture effect). Технические предложения по построению двухчастотных радиомаяков были опубликованы в ряде работ, в частности в [4, 5]. Двухчастотный режим ILS предполагает формирование двух высокочастотных сигналов: основного – сигнала узкого канала (УК) и дополнительного – сигнала широкого канала (ШК). Задачей УК является формирование узких угловых зон: зоны курса в пределах ±2° относительно оси ВПП и зоны глиссады в пределах ±0,5° относительно угла глиссады. В этих зонах задается линейная зависимость между величиной информационного параметра (РГМ) и угловым отклонением самолета от заданной траектории. Широкий канал обеспечивает пилота информацией во всей остальной зоне действия, «указывая» на- правление «правильного» движения к траектории снижения. При этом несущая частота сигнала ШК смещена относительно частоты сигнала УК на 5–15 кГц.

Путем формирования ДН специальной формы добиваются существенного превышения уровня сигналов УК по сравнению с уровнем сигналов ШК в пределах узкой зоны в окрестности глиссады (±2° в азимутальной плоскости и ±0,5° в угломестной плоскости) и существенного превышения уровня сигналов ШК по сравнению с уровнем сигналов УК в пределах зоны наведения.

Двухчастотные радиомаяки используются за рубежом и в нашей стране давно. Однако детального анализа формирования их зоны действия в литературе не приведено. В зарубежных работах имеются ссылки на ведомственные отчеты, недоступные специалистам в нашей стране. Настоящей работой устраняется указанный пробел. Целью работы является вывод приближенных соотношений для вычисления РГМ, которые могли бы быть использованы разработчиками радиомаяков для оценок и интерпретации зависимости РГМ от соотношения сигналов в узком и широком каналах, для приближенной оценки величины искривлений линии курса и глиссады, которые оказались бы полезными непосредственно на аэродроме специалистам, выполняющим ввод радиомаяков в эксплуатацию, преподавателям и студентам при изучении принципа работы двухчастотного радиомаяка.

Постановка задачи

Пусть КРМ и ГРМ расположены на плоской горизонтальной поверхности (см. рис. 1). Для определенности будем далее анализировать работу КРМ. Введем в рассмотрение сферическую систему координат с осью Оz , перпендикулярной к поверхности Земли. Начало координат находится на продолжении оси ВПП, в точке, являющейся проекцией центра антенны КРМ на упомянутую плоскость. Азимутальный угол ф отсчитывается от оси ВПП.

Антенно-фидерный тракт КРМ совместно с передающим устройством формируют в пространстве ниже следующие сигналы.

Сигнал «несущая частота плюс боковые частоты» (НБЧ) узкого канала (НБЧ УК) U нбч ( ф , t ) :

U нбч ( ф , t ) = x ( ф , t ) cos (^юУК t + У ^ук) ,                                                                 (1)

где x (ф, t) = FXfa) • [1 + m cos (^1t) + m cos (^2t)];                                                (2)

ф - азимутальный угол; t - время; Е _н уч ( ф ) - диаграмма направленности антенны КРМ в азимутальной плоскости по сигналу НБЧ узкого канала; ю ук - угловая частота несущей сигнала узкого канала; у ук - начальная фаза несущей частоты сигнала узкого канала; m - глубина модуляции сигнала УК (ШК) на входе антенны; Ц = 2 n f 1 ; Q ₂ = 2 n f 2 •

Сигнал «боковые частоты» (БЧ) узкого канала (БЧ УК) U буч ( ф , t ) :

U бч ( ф , t ) = У ( ф , t )cos ( ю ^ук t — У ук ) ,                                                                  (3)

где у (ф, t) = а ук Ебуч (ф) • [ m cos (Q1t) - m cos (Q2t)],                                                    (4)

Е буч ( ф ) - диаграмма направленности антенны КРМ в азимутальной плоскости по сигналу БЧ узкого канала; a ^ук – коэффициент, равный отношению амплитуд напряжений сигналов с угловыми частотами Q 1 и Q 2 модуляции в каналах БЧ и НБЧ узкого канала на входе антенны (величиной коэффициента a ^ук регулируют крутизну зоны УК).

Сигнал «несущая частота плюс боковые частоты» широкого канала (НБЧ ШК) U шбч ( ф , t ) :

U ш ^к _ч ( ф , t ) = у ( ф , t ) cos | ю ' + у ^шк ) ,                                                                 (5)

где v (ф, t) = бЕнб^ф) • [1 + m cos (Q1t) + m cos (Q21)];                                                (6)

b – коэффициент, равный соотношению амплитуды сигнала НБЧ ШК к амплитуде сигнала НБЧ УК на входе антенны; ^ _н ШЧ ( ф ) - диаграмма направленности антенны КРМ в азимутальной плоскости по сигналу НБЧ широкого канала.

Сигнал «боковые частоты» широкого канала (БЧ ШК) U бч ^к( ф , t ):

Uбшчк (ф, t ) = w (ф, t )cos |м '-^шк), (7) где w (ф, t) = а шк 6^6Шк(ф) •[ m cos (^1t)- m cos (^2t)]; (8) aшк – коэффициент, равный отношению амплитуд напряжений сигналов с угловыми частотами Q| и Q2 в каналах БЧ и НБЧ широкого канала на входе антенны (величиной коэффициента ашк регулируют уровень РГМ в широкой зоне); ^бШк(ф) - диаграмма направленности антенны КРМ в азимутальной плоскости по сигналу БЧ широкого канала.

Как следует из (1) и (3), разность фаз сигналов НБЧ и БЧ узкого канала равна 2^^. Из (5) и (7) следует, что разность фаз сигналов НБЧ и БЧ широкого канала 2 ^ ^шк. Принятый в (1), (3), (5), (7) учет разности фаз сигналов НБЧ и БЧ не нарушает общности анализа, однако, упрощает в дальнейшем преобразования.

Принятый на борту самолета суммарный сигнал проходит через входные цепи приемника, смеситель, усилитель промежуточной частоты и поступает на вход линейного детектора. Согласно [5], на выходе линейного детектора, включающего в себя низкочастотный фильтр, будем наблюдать сигнал, описываемый модулем огибающей суммарного сигнала, в [6] называемым физической огибающей. Медленно меняющаяся огибающая не искажается НЧ-фильтром. Далее сигнал поступает на вход полосно-пропускающих фильтров, которые выделяют составляющие с частотами f ₁ и f ₂ . Амплитуды напряжений выделенных колебаний нормируются относительно постоянной составляющей суммарного сигнала. Выделенные нормированные составляющие сигнала проходят через выпрямители, на выходе которых формируется разностное напряжение, поступающее на микроамперметр, который показывает величину тока, пропорциональную РГМ. Коэффициент пропорциональности между величиной тока и РГМ одинаков для всех бортовых приемников ILS. Поэтому при летных проверках параметров КРМ и ГРМ значения РГМ измеряют в микроамперах, не переводя их в проценты.

Нашей задачей является нахождение зависимости РГМ ( ф ) при различных соотношениях амплитуд сигналов широкого и узкого каналов b , при разных значениях разности фаз между сигналами НБЧ и БЧ в упомянутых каналах (2 ^ ^ук в узком канале, 2 ^ ^шк в широком канале).

Метод решения

Принятый на борту самолета суммарный сигнал U ² ( ф , t ) на входе приемника является узкополосным сигналом. Сигнал U ² ( ф , t ) подвергается линейному детектированию. Для нахождения сигнала на выходе линейного детектора воспользуемся методикой, используемой для описания детектирования квазигармонических колебаний [5]. Для точного нахождения амплитуд колебаний Q _| и Q 2 , выделяемых низкочастотными фильтрами, и постоянной составляющей используем разложение модуля огибающей суммарного сигнала в ряд Фурье. Глубину модуляции колебаниями с частотой Q _| ( Q 2 ) найдем как частное от деления амплитуд колебаний Q _| ( Q 2 ) к постоянной составляющей.

Для приближенного нахождения амплитуд колебаний Q _| и Q 2 , воспользуемся разложением модуля огибающей суммарного сигнала в ряд Маклорена.

Решение задачи

Выберем в качестве опорной угловой частоты сигнала, получаемого в результате суммирования сигнала узкого и сигнала широкого каналов U ² ( ф , t ) , частоту to o :

to o =

to ™ + to ^yк 2

Введем обозначение top частоты, равной половине разности частот несущих частот широкого toшк и узкого to^ каналов:

^to p

to ™ -to ^yк 2

Тогда сигнал U ² ( ф , t ) на входе приемника может быть представлен в следующем виде:

и ^Е ( ф , t ) = и ,^ук_ч⁽ Ф , t ) + и бчХ Ф , t ) + и нбч ( ф , t ) + U _б ш ^к ( ф , t ) =

= F ^Убч ( ф ) ■ [ 1 + m cos ( ^ t ) + m cos ( ^ 2 t ) ] cos ( ( to ₀ - to _p) t + v ^ук ) +

+ aF ^ ( ф ) ■[ m cos ( Q ₁ t ) - m cos ( Q ₂ t ) ] cos ( ( to ₀ -to _p) t - v ^ук) +

+ bF ™ ( ф ) ■ [ 1 + m cos (^ t ) + m cos ( ^ ₂ t ) ] cos ( ( to ₀ + to _p) t + v ™ ) +

+ baF ™ ( ф ) ■ [ m cos ( Q ₁ t ) - m cos ( Q ₂ t ) ] cos ( ( to ₀ + to _p) t - v ™ ) .                               (11)

Преобразуем выражение U ² ( ф , t ) в (11) к виду

U ² ( ф , t ) = A ( ф , t ) cos ( to ₀ 1 ) - B ( ф , t ) sin ( to ₀ 1 ) .                                                         (12)

Как известно, узкополосные сигналы представляют собой квазигармонические колебания.

Функцию A (ф, t) принято называть синфазной амплитудой узкополосного сигнала U2 (ф, t) при заданной опорной частоте to0, а функцию B (ф, t) - его квадратурной амплитудой.

Модуль огибающей узкополосного сигнала выражается через синфазную и квадратурную амплитуды сигнала U ² ( ф , t ) на входе приемника:

U (ф, t ) = V A 2 (ф, t) + B 2 (ф, t).(13)

Выделим в суммарном сигнале синфазную и квадратурную амплитуды сигнала. Запишем

U ² ( ф , t ) с учетом ранее введенных обозначений (2), (4), (6), (8):

U ² ( ф , t ) = x ( ф , t ) cos ( ( to ₀ - to _p ) t + v ^ук ) + y ( ф , t ) cos ( ( to ₀ - to _p ) t - v ^ук ) +

+v (ф, t) cos ((to0 +top) t + v™) + w (ф, t) cos ((to0 +top) t -v™).(14)

Выполнив в (14) тригонометрические преобразования, получим:

A ( ф , t ) = x ( ф , t )cos ( v ^ук -to _p t ) + y ( ф , t )cos ( -v ^ук -to _p t ) +

+v (ф, t )cos (vшк +top t) + w (ф, t )cos (-vшK +top t);(15)

B ( ф , t ) = x ( ф , t )sin ( v ^ук -to _p t ) + y ( ф , t )sin ( -v ^ук -to _p t ) +

+v (ф, t )sin (vшк +top t) + w (ф, t )sin (-vшK +top t).(16)

A ² ( ф , t ) + B ² ( ф , t ) = x ²( ф , t ) + y ² ( ф , t ) + v ² ( ф , t ) + w ² ( ф , t ) + 2 x ( ф , t ) y ( ф , t ) cos 2 v ^ук +

+ 2 x ( ф , t ) v ( ф , t )cos ( v ^ук -v ^шк - 2 to _p t ) + 2 x ( ф , t ) w ( ф , t )cos ( v ^ук + v™ - 2 to _p t ) +

+ 2 y ( ф , t ) v ( ф , t )cos ( -v^ук -v ™ ^к - 2 to _p t ) + 2 y ( ф , t ) w ( ф , t )cos ( -v ^ук + v™ - 2 to _p t ) +

+2 v (ф, t) w (ф, t )cos2v™.(17)

Точные значения РГМ ( ф )

Для точного вычисления разности глубин модуляции суммарного сигнала РГМ“ (ф) вос пользуемся разложением функции U (ф, t)

в ряд Фурье. Функция U (ф, t) является периодиче- ской функцией с периодом T :

1 T = —c .

Обозначим частоту, равную 30 Гц, буквой с нижним индексом 0: f0 , а соответствующую угловую частоту: Qo, (Qo = 2пf0). Тогда угловые частоты Q,n Q2 представляются как 3-я и 5-я гармоники модуля огибающей суммарного сигнала (Q1 = 3^0, Q2 = 5Qo)- Функция U(ф,t) (13) является четной функцией переменной величины t , следовательно, в разложении будут отлич- ными от нуля только косинусоидальные составляющие сигнала.

Амплитуда M 1 ( ф ) колебания с частотой 90 Гц равна:

TT

22                       22

M 1 ( ф ) = — j U ( ф , t ) cos( Q 1 t ) dt = — j U ( ф , t ) cos(3 Q ₀ t ) dt .

Сделаем в подынтегральном выражении в (18) замену переменной Q _o t = n ,

зультате верхний предел интеграла в (18) при интегрировании по переменной n

dt = d 7 . в ре-

Q o

T

^(пР^и t = -) Р^а-

Т вен Qo — = п. Нижний предел равен -п.

M 1 ( ф ) =

T Q o

п                           1 п j U(ф,n)cos3ndn = — j U(ф,n)cos3ndn.

—п

—п

Аналогично получим, что амплитуда M2 (ф) колебания с частотой 150 Гц и постоянная со ставляющая Mо(ф) равны соответственно:

1п

M2<ф) = - (U(ф,n)cos5ndn , Mо(ф) =— fu(ф,n)dn.

п J2п

-п-п

Глубина модуляции огибающей сигналом 90 Гц [150 Гц] представляет собой частное от деления амплитуды M 1 ( ф ) [ M ₂ ( ф ) ] на постоянную составляющую M о( ф ):

, х M, (ф)        , . M2 (ф)          У / .        , ., .

тх(ф)=irbi; m2(ф)=тт^;РГМ (ф)=m1 (ф)-m2(ф).

M 0 ( ф )          M 0 ( ф )

Формулы (19)–(21) будут далее использоваться для вычислений точных значений функции РГМ “ ( ф ) . Однако получаемые при этом результаты не удобны для выявления физических закономерностей в формировании РГМ ^Е( ф ) при совместной работе УК и ШК. С целью получения более наглядных соотношений ниже найдем приближенные соотношения, более удобные для этих целей.

Приближенные значения РГМ ( ф )

Далее для целей физической интерпретации работы двухчастотного радиомаяка выведем приближенную формулу для вычисления РГМ ( ф ) . Выполним следующие преобразования. Возведем в квадрат функции A ( ф , t ) и B ( ф , t ), найдем сумму A ² ( ф , t ) + B ² ( ф , t ) . Корень квадратный из суммы (13) описывает модуль огибающей сигнала на входе НЧ-фильтра [5]:

A ² ( ф , t ) + B ² ( ф , t ) = x ( ф , t )² + у ( ф , t )² + v ( ф , t )² + w ( ф , t )² + 2 x ( ф , t ) у ( ф , t )cos2 y ук + + 2 x ( ф , t ) v ( ф , t )cos ( ф ук -ф ^шк - 2 ю р t ) + 2 x ( ф , t ) w ( ф , t )cos ( ф ук + ф ^шк - 2 ю р t ) + + 2 у ( ф , t ) v ( ф , t )cos ( -ф ^ук -ф ^шк - 2 ю р t ) + 2 у ( ф , t ) w ( ф , t )cos ( -ф ук + ф ^шк - 2 ю р t ) +

+ 2 v ( ф , t ) w ( ф , t ) cos 2 ф ^шк.

Сигнал на выходе НЧ-фильтра не будет содержать колебаний с разностной частотой 2 ю _р t . Обозначим амплитуду сигнала на выходе фильтра:

и нч ( ф , t ) = V A ² ( ф , t ) + B ² ( ф , t )

нч

На выходе НЧ-фильтра получим

A ² ( ф , t ) + B ² ( ф , t )| нч = x ( ф , t )² + у ( ф , t )² + v ( ф , t )² + w ( ф , t )² + + 2 x ( ф , t ) у ( ф , t ) cos 2 ф ^ук + 2 v ( ф , t ) w ( ф , t ) cos 2 ф ^шк.

Или, учитывая ранее введенные обозначения (2), (4), (6), (8):

A ² ( ф , t ) + B ² ( ф , t )| = { ^ НУК _ч ( ф ) -[ 1 + m cos ( O j t ) + m cos ( Q ₂ 1 ) ] } +

+ { a ук F ^^ ( ф ) -[ m cos ( ^ t ) - m cos ( ^ 2 t ) ] } +

+ { bF ^Z ( ф ) ’ [ 1 + m cos ( O 1 t ) + m cos ( Q ₂ 1 ) ] } +

+ { ba шк F ^ ( ф ) -[ m cos ( ^ 1 t ) - m cos ( ^ 2 1 ) ] } +

+ 2 { F^ ( ф ) ' [ 1 + m cos ( ^ 1 t ) + m cos ( O ₂ 1 ) ] } - a ук F ^ ( ф ) - [ m cos ( Q 1 t ) - m cos ( Q ₂ 1 ) ] cos 2 ф ук +

+ 2 bF ^ ( ф ) - [ 1 + m cos ( Q 1 t ) + m cos ( Q ₂ 1 ) ] - ba _шк F ™ ( ф ) - [ m cos ( Q 1 t ) - m cos ( Q ₂ 1 ) ] cos 2 ф ^шк =

= |[ F нУK _I( ф ) ] ² + [ Ь^ ^ншк ( ф ) ] ² }[ 1 + m cos ( Q 1 t ) + m cos ( П 2 1 ) ] 2 +

⁺ { ^{[ a} ук ^F б ^уk( ф ⁾ ] ^+[ ba шк F a™^ ) ] } ^{[ mcos} ( ^ 1 t ) ^{- mcos} ( ^ 2 t ) ] ^{2 +}

[ F нУkч ( ф ) - a ук F бУk ( ф ) ] cos2 ф +[ bF™(4>) - ba ш _К 7 ^бш ^к( р ) ] cos2 ф ^шк } x

x [ 1 + m cos Q 1 1 + m cos Q ₂ 1 ][ m cos Q 1 t - m cos Q ₂ 1 ] .                                           (24)

В полученном выражении (24) сгруппируем слагаемые. Независящую от времени величину обозначим c ² ( ф ) . Множители перед функциями cos( Q 1 t ) и cos( Q ₂ 1 ) обозначим d ( ф ) и f ( ф ) , соответственно. Сумму слагаемых, содержащих комбинационные частоты 2 ^ 1 , 2^, ^ 1 -^ 2 , Ц +Q 2 обозначим g ( ф ) .

22  22

c ² ( ф ) = ( 1 + m ² ) { [ ^ Убч ( ф ) ] + b ² [ ^ шк ( ф ) ] } + m ² a ² { [ ^ ^( ф ) ] + b ² [ ^ шк ( ф ) ] } ;

d ( ф ) = 2 m { [ ^ нбч ( ф ) ] ² + b ² [ F ^ ( ф ) ] ² +

+ a [ F^ ( ф ) F бУК ( ф ) cos 2 ф ^ук + b ² F^ ( ф ) F ^ ( ф ) cos2 ф ^шк ] } ;

f ( ф ) = 2 m { [ F нУЧ ( ф ) ] ² + b ² [ F нШК ( ф ) ] ² -

- a [ F _нУК_I ( ф ) F б ^у ч ^к( ф )cos2 ф ^ук + b ² F ^ ( ф ) F бШ ^К( ф )cos2 ф ^шк ] } .

Полагая в (13) величину c ² ( ф ) большой по сравнению с d ( ф ) , f ( ф ) и g ( ф , t ) , вынесем ее из-под корня квадратного и затем для вычисления корня квадратного воспользуемся разложением функции ( 1 + x ) ² в ряд Маклорена [7]:

х1 л 11

(1 + x)2 — 1 +— xx v ’        22

1 - 1 - 3 з

+----- x

2 - 4 - 6

—

1 - 1 - 3 - 5 ₄ ------------x + ...

2 - 4 - 6 - 8

Ограничиваясь первым членом разложения функции U нч ( ф , t ) , получим

и нч ( ф , t ) — V A ² ( ф , t ) + B ² ( ф , t )

« c f 1 + l

d ( 2 )cos( Q 1 t ) + ^{f (} ф ^)cos ( Q t ) + g ( ф , t ) 2 c ²( ф )           2 c ²( ф )       2 c ²( ф ) ,

Следовательно, величина РГМ ^Х ( ф ) приближенно равна:

РГМ ^Е ( ф ) « d ^{(ф) f (ф)} ;                                                               (30)

2 c ²

2 am [ F _Hук_ч ( ф ) F ₆уk ( ф )cos2 v ук + b ² F _Hш» F ₆ш^к ( ф )cos2 v ^шк 1

РГМ^Е ( ф ) «-------- ^L б ₂ б --------------------z--------------------^]-----.       (31)

( i + m ² ) 1 ^[ ^ ^( ф ) ]² + b ^{2 [} Р шЧ С ф ) ]²)+ m ² a ² 1 ^[ Р уЧЧ ф ) ]² + b ^{2 [ F} б^IЧ ^к( ф ) ]²)

Анализ результатов

Частные случаи

Рассмотрим первый частный случай . Пусть радиомаяк работает в одночастотном режиме ( b — 0), причем сигналы НБЧ и БЧ, как это требуется по принципу работы радиомаяка, синфазны ( v ук = 0). Тогда

U нч ( ф , t ) — A ² ( ф , t ) + B 2 ( ф , t ) — x ² ( ф , t ) + y ²( ф , t ) + 2 x ( ф , t ) y ( ф , t ),                                 (32)

то есть огибающая U нч ( ф , t ) суммарного сигнала равна:

и нч ( ф , t ) — J A ² ( ф , t ) + B ² ( ф , t )

нч

— | x ( ф , t ) + y ( ф , t )|.

Следовательно, инч (ф, t) — IfX (ф) - [1 + m cos (Q11) + m cos (Q21)] + ару (ф) - [ m cos (Q11) — m cos (Q21 )]|

— | р ."ч ( ф)| - 1 +

m [ 1 + aF^' l      Р нбч ( ф ) J

cos ( Q] t ) + m 1 — a ^Fб^{ч ( ф )}

^{( 1} ) l      Р нбч ( ф ) J

cos ( Q ₂ 1 ) .

Пусть в некотором секторе углов ф1 <ф<ф2 функция Рнуч(ф)>0, Рбук(ф)<Рнуч(ф). Тогда, учитывая, что 0 < а < 1, m — 0,4, получим, что в (34) первый и второй множители являются положительными величинами. Следовательно, инч (ф, t) — РН6Ч(ф) 1 + m f1 + аРбч(ф)

L l     ^р нбЧ ( ф ) J

cos Q 1 1 + m 1

—

F УК ( ф ) ) a бч

l      Р нбч ( ф ) J

cos Q ₂ 1

;

.        F 2^к(ф)

РГМ ук ( ф ) — 2 ma ——--- , при ф 1 < ф < ф ₂.

^Р нбч ^{( ф )}

Пусть при некотором значении ф — ф3 имеем РнуЧ(ф3) — 0. Тогда инч (ф, t) — |аРбук (фз) - [m cos (Qit) — m cos (Q21 )]| —

— ар бук ( ф з )| m cos ( Q 1 t ) — ар Чк ( ф з )| m cos ( Q ₂ 1 ) .                                           (37)

Следовательно,

РГМ ук ( ф ₃ ) — 0.                                                                            (38)

F ук ( ф )

Пусть теперь в некотором секторе углов ф₄ < ф <  ф₅, a —бч—- >  1.

F M

Однако, пусть при любом значении переменной t выражение под знаком модуля в (34) имеет положительное значение. Тогда знак модуля в (34) может быть опущен. При этом запишем выражение U нч ( ф , t ) в таком виде, чтобы множитель, стоящий перед функцией cos ( Q 2 1 ) был бы положительной величиной:

Г fUнч (ф,t) = FX^) 1 + m 1 + a

f

В (39) величина m a

k

k

F бУK ( ф ) F нУ> ^K ч ( ф )

FM1 ^УЧ(ф) J

—

cos ( Q 1 t ) — m

L F ббчк ( ф ) a k <ч ( ф )

—

1          ]

1 cos (^Q ₂ t ) .

J           _

1 представляет собой коэффициент модуляции (по определе-

J

нию коэффициент модуляции – величина положительная). Стоящий перед этой величиной знак минус означает, что фаза сигнала с частотой Q отличается от фазы аналогичного сигнала в сигнале НБЧ на 180°. Фаза сигнала при определении глубины модуляции не принимается во внимание. Тогда из (39) следует

РГМ ук ( ф ) = 2 m , при ф ₄ <ф<ф ₅. (40)

F Ук ( ф )

Пусть далее в некотором секторе углов ф₆ < ф <  ф₇ a —бч—- < — 1, однако, при любом зна- ^ нб»

чении переменной t выражение под знаком модуля имеет положительное значение. Тогда поступим аналогично предыдущему случаю. Запишем выражение U нч ( ф , t ) в таком виде, чтобы множитель, стоящий перед функцией cos Q 1 t в круглых скобках был бы положительной величиной:

Uнч (ф, t ) = ^(ф) 1 — m

f 1 Лб^(ф) 1

— 1 — a

k      ^уч(ф) J

cos ( Q 1 t ) + m

f

1—

k

n <(ф)1

a

^уч(ф) J

cos ( Q ₂ t ) .

В (41) положительная величина m — 1 — a

CM 1 ^ 5бч (ф> ^J

представляет собой коэффициент моду-

ляции, а стоящий перед этой величиной знак минус означает, что фаза сигнала с частотой Q 1 отличается от фазы аналогичного сигнала в сигнале НБЧ на 180°. Тогда из (39) следует:

РГМ ук ( ф ) = — 2 m , при ф ₆ <ф<ф ₇.                                                (42)

В тех случаях, когда выражение под знаком модуля является знакопеременным, вычисление функции РГМ ( ф ) следует выполнять по формулам (19)-(21) разложения функции U нч ( ф , t ) в ряд Фурье. Случай, когда функция под знаком модуля в пределах периода меняет знак, соответствует ситуации с перемодуляцией сигнала. Как следует из численных экспериментов, приведенных ниже, в этих случаях, — 2 m <  РГМ ( ф ) <  2 m . Таким образом, величина 2 m является наибольшим значением функции РГМ ( ф ) , а величина — 2 m является наименьшим значением этой функции.

Рассмотрим второй частный случай. Пусть радиомаяк по-прежнему работает в одночастотном режиме (b = 0). Однако, теперь сигналы НБЧ и БЧ сдвинуты относительно друг друга по фазе (уук ^ 0). Такой режим работы наблюдается в процессе настройки радиомаяка на аэродроме. Тогда из (31) следует

Р_ГМ ук (_ф) ^      ² amF^ ⁽ ф ) ^F бч ⁽ ф )^{cos 2} Ф ^ук     .

( 1 + m ² ) Г ^ нбч ( ф ) ] ² + m 2 a 2 Г ^ б ^у _ч ^к( ф ) ] 2

Учитывая то, что a <  1, m ² <<  1, из (36) получим

РГМ ук ( ф ) « 2 am F ^) cos2 _V ук . ^{V ?}       F нУч ( ф )

Это соотношение обычно используется в практической работе при настройке КРМ и ГРМ на аэродроме, а также для приближенной оценки искривлений линии курса и глиссады. На рис. 2 F ^у ( ϕ )

приведены нормированные относительно величины 2 am _у^ч_к    зависимости РГМ от величины

2 ψ ^ук при различных значениях a , найденные по точным формулам (19)–(21). Как видно из графиков на рис. 2, найденные по точным формулам значения РГМ всегда меньше значений РГМ, полученных по приближенной формуле. На рис. 3приведена зависимость нормированной ошибки вычисления РГМ по приближенной формуле от величины 2 ψ ^ук . Как видно из графиков, абсолютное значение ошибки растет с ростом величины 2 ψ ^ук . Однако, при обычно выставляемых при настройке КРМ значениях a , ошибка не превышает 5 %, что на практике допустимо.

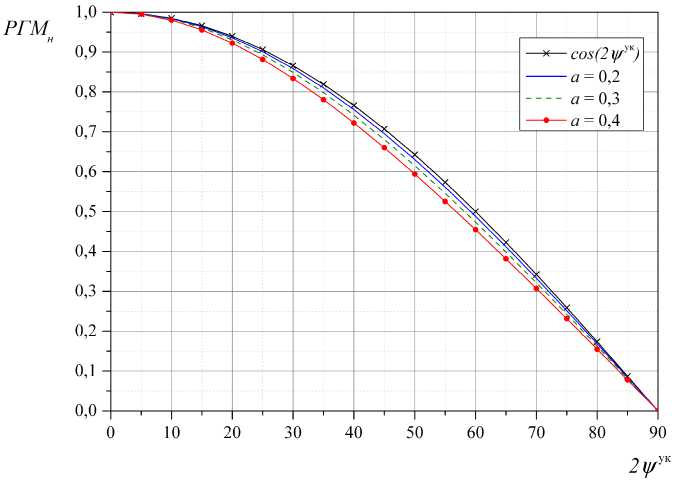
Рис. 2. Зависимость нормированной величины РГМ_н от разности фаз 2 ψ ^ук сигналов БЧ и НБЧ

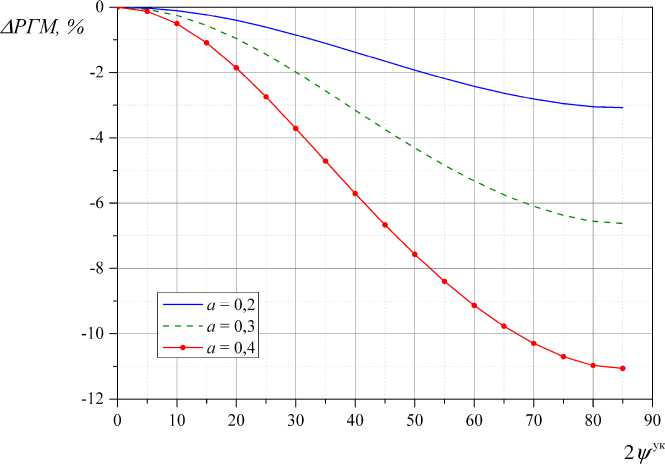
Рис. 3. Зависимость относительной ошибки вычисления РГМ по приближенной формуле от разности фаз 2 ψ ^ук

Рассмотрим третий частный случай. Радиомаяк работает в двухчастотном режиме ( b ^ 0) .

Пусть    = ^шк = 0, 0 < b < 1, ь^ншч(Ф)< F^ (ф), bF™ (ф)< F^ (ф).

Тогда, влияние второго слагаемого в числителе формулы (31) оказывается менее значимым, чем первого (дополнительное ослабление в b раз). Таким образом, мы наблюдаем явление подавления двух слабых сигналов F _и ШK ( ф ) , Л б'Чк ( ф ) двумя сильными сигналами F _и уK _ч ( ф ) , F ^ ( ф ) •

Обратимся снова к соотношению (31). Преобразуем его следующим образом. В числителе первое слагаемое умножим и разделим на F ^ ( ф ) , второе слагаемое умножим и разделим на

F И55ч ( ф ) , затем выполним в числителе замену:

2am Fбч (ф) cos2vук = РГМук (ф);

F^ (ф)

2am Uбч (ф) cos2Vшк = РГМшк (ф).

U и™ ( ф )

В результате получим ргму- (ф)Г Fук (ф)]2 + ь2 [ FиШ; (ф)]2 РГМшк (ф)

РПМ1(ф) =---------L------X----L------Г---------.(47)

[ Fи5ч (ф)] + b2 Г F.“ (ф)]

Запишем соотношение (47) в более компактном виде, с этой целью числитель и знаменатель

2                                                Fшк (ф)

разделим на величину Г F у? ( ф ) ] , кроме того, введем обозначение: а ( ф ) = b — ^{б у} . Тогда соот- ^{L ]}                                                  F ( ф )

ношение (23) примет вид

РГМЕ(ф) =

РГМук (ф) + [а(ф)]2 РГМшк (ф)

1 + [а(ф)]2

Как видно из (48), если отношение а ( ф ) амплитуды сигнала НБЧ ШК к амплитуде сигнала НБЧ УК в некотором направлении или в некотором секторе азимутальных углов меньше 1, то вклад РГМ^шк ( ф ) в величину РГМ ^Е суммарного сигнала уменьшается в а ( ф ) раз. Напротив, если в некотором направлении или в некотором секторе азимутальных углов а ( ф ) больше 1, то вклад РГМ^шк ( ф ) увеличивается в а ( ф ) . При а ( ф ) = 1 вклады РГМ^ук ( ф ) и РГМ^шк ( ф ) в РГМ “ ( ф ) не имеют весовых коэффициентов.

Общий случай

На рис. 4-6 приведены ДН антенны КРМ и зависимости РГМ ук ( ф ) , РГМ^шк ( ф ) , РГМ “ ( ф ) в общем случае, когда на значение параметров двухчастотного радиомаяка не вводятся ограничения. В качестве антенны рассматривается неэквидистантная антенная решетка (АР) полуволновых вибраторов с общим рефлектором с широко используемым в КРМ амплитудно-фазовым распределением. Причем влияние рефлектора на формирование ДН не учитывается, т. е. вычисляется множитель антенной решетки, умноженный на ДН вибратора в свободном пространстве. При вычислениях ДН предполагалось, что амплитуды токов в вибраторах для каждого из четырех сигналов нормированы относительно величины, равной корню квадратному из суммы квадратов амплитуд токов. Принято, что v ук = V ™ = 0 •

На рис. 4 приведены ДН антенны для сигналов НБЧ УК, БЧ УК и РГМук (ф). ДН НБЧ УК имеет колокообразный вид с максимумом в направлении оси ВПП (ф = 0°), с низким уровнем бокового излучения в секторе углов ф < -7° и в секторе 7° < ф. ДН БЧ УК имеет «разностный» вид с большим уровнем излучения в указанных выше секторах, однако, не превышающим уровень -23 дБ. Величина РГМук (ф) монотонно растет в пределах от -5 до +5°. За пределами ука- занного сектора углов функция РГМук(ф) имеет осциллирующий характер с включением узких секторов углов, в которых она имеет постоянное значение, равное либо -2m , либо +2m . При указанных ДН уровень излучения в направлении местных предметов, расположенных в секторах ф < -7° и 7° < ф значительно ослаблен, что гарантирует малое влияние этих местных предметов на поведение линии курса. Однако, в секторе углов (–35°, +35°) существует множество ложных курсов.

На рис. 5 приведены ДН антенны для сигналов НБЧ ШК, БЧ ШК и РГМ^шк ( ф ) . ДН НБЧ ШК имеет вид пьедестала с углублением в секторе углов - 10 ° < ф <  10 ° . ДН БЧ ШК имеет «разностный» вид с большим уровнем излучения вне указанных секторов. Величина РГМ^шк монотонно растет в пределах от -8 до +8°. За пределами указанного сектора углов функция РГМ^шк( ф ) имеет почти постоянное значение. В этих секторах отсутствуют ложные курсы.

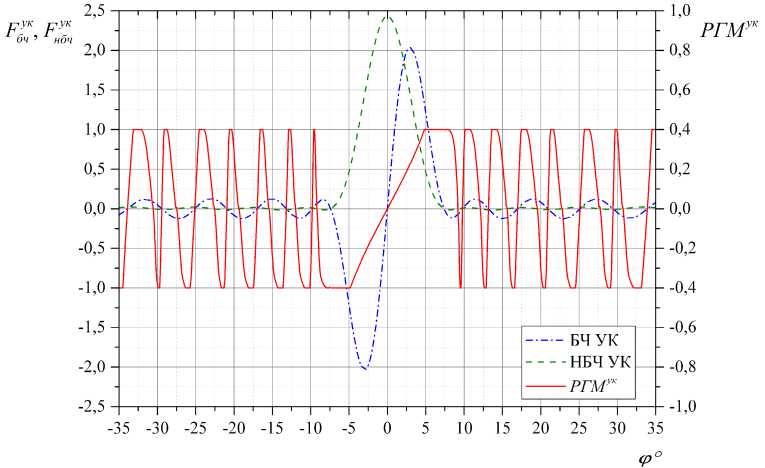
Рис. 4. ДН антенны для сигналов БЧ УК, НБЧ УК и РГМ ук ( ф ) ; m = 0,2; а ^ук =0,4

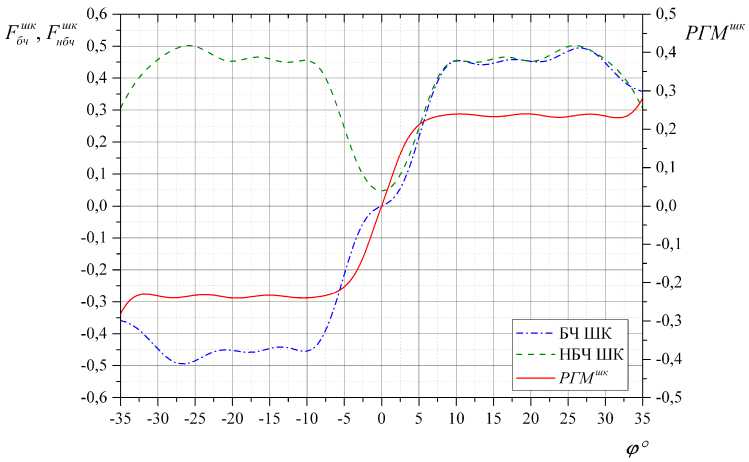
Рис. 5. ДН антенны для сигналов БЧ ШК, НБЧ ШК и РГМ шк ( ф ) ; m = 0,2; а ^шк = 0,6

На рис. 6 приведены зависимости РГМ ^Е ( ф ) при различных значениях коэффициента а ^шк ( b = 0,7). Как видно из рассмотрения графиков на рис. 6, в секторе углов - 5 ° < ф <  5 ° наблюдается плавный, монотонный рост РГМ ^s ( ф ). В этом секторе осуществляется работа с узким каналом. За пределами указанного сектора углов функция РГМ ^Е ( ф ) имеет почти постоянное значение. Уровень постоянного значения определяется значением коэффициента a ^шк . В этом секторе осуществляется работа с широким каналом.

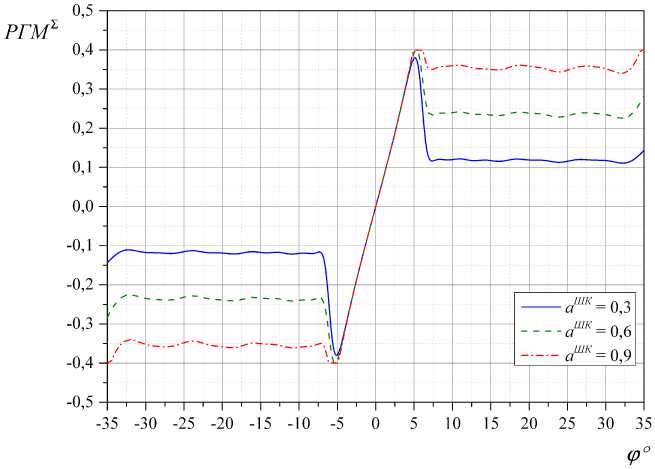
Рис. 6. Зависимость РГМ ^Σ ( ϕ ) ; m = 0,2; а ^ук = 0,4; b = 0,7

Выводы

• 1.    Найдены соотношения в виде квадратур для точного вычисления РГМ ^Е ( ф ) в зоне действия двухчастотного радиомаяка (КРМ или ГРМ) при любых соотношениях между комплексными амплитудами напряженностей полей сигналов узкого и широкого каналов, излучаемых антеннами с заданными диаграммами направленности.

• 2.    Получены соотношения для приближенного вычисления РГМ ^Е ( ф ) сигналов на выходе линейного детектора. Полученные соотношения обобщают известные соотношения для случая линейного детектирования гармонического сигнала в присутствии помехи на случай, когда на вход линейного детектора одновременно поступает «сильный» сигнал, модулированный по амплитуде двумя низкочастотными тонами, и «слабый» сигнал с точно такой же модуляцией. Показано, что «слабый» сигнал оказывается ослабленным в число раз, равное соотношению амплитуд «сильного» и «слабого» сигналов ( b раз).

• 3.    Проведено сравнение результатов вычисления РГМ ук ( ф ) по точной и приближенной формулам для одночастотного радиомаяка. Показано хорошее совпадение результатов в случае, когда отношение амплитуды сигнала БЧ к амплитуде сигнала НБЧ меньше единицы.

• 4.    Найдены соотношения для приближенного вычисления РГМ ^Е ( ф ) двухчастотного радиомаяка по известным РГМ ук ( ф ) узкого канала и РГМ^шк( ф ) широкого канала и известному соотношению амплитуд НБЧ широкого и НБЧ узкого каналов.

• 5.    Численными экспериментами показано, что в зоне действия радиомаяка величина РГМ ^Е ( ф ) может изменяться в пределах от - 2 m до + 2 m , где m - глубина модуляции сигнала НБЧ сигналами с угловыми частотами Q 1 и Q ₂.

• 6.    Показано, что в зоне действия КРМ сигналы узкого и широкого каналов меняются ролями в отношении «слабый», «сильный». В узкой угловой рабочей зоне в окрестности направления

• 7.    Показано, что при работе двухчастотного КРМ в секторе углов - 5 ° < ф <  5 ° наблюдается плавный, монотонный рост РГМ ^Х ( ф ). За пределами указанного сектора углов функция РГМ ^Х ( ф ) имеет почти постоянное значение. Уровень постоянного значения определяется значением коэффициента а ^шк, равного отношению амплитуд напряжений сигналов с частотами Q 1 и ^ в каналах БЧ и НБЧ широкого канала на входе антенны.

вдоль оси ВПП сильным сигналом является сигнал узкого канала, слабым – сигнал широкого канала. За пределами узкой угловой зоны сильным сигналом является сигнал широкого канала, слабым – сигнал узкого канала. В переходной зоне сигналы узкого и широкого каналов равноценны, при этом обеспечивается плавный ход функции РГМ ^Е ( ф ) при переходе из одной зоны в другую.