Моделирование работы гиперспектрометра, основанного на схеме Оффнера, в рамках геометрической оптики

Эффективность использования данных дистанционного зондирования Земли (ДЗЗ) может быть существенно повышена за счет детального анализа информации на разных длинах волн [1-3]. Для этого разрабатываются малогабаритные изображающие гиперспектрометры, имеющие высокое пространственное и спектральное разрешение. До появления видеоспектрометров спектры отражения и излучения поверхности Земли мало использовались в качестве идентификационных признаков [1 –4], хотя изучались десятки лет и были хорошо известны. Это было связано с тем, что авиационные спектрометры имели низкое геометрическое разрешение, давали информацию только вдоль линии полёта и позволяли судить о спектральных свойствах лишь достаточно протяжённых объектов. Появление видеоспектрометров связано с развитием новых технологий: с разработкой матричных приёмников, а также с появлением полихро-маторов, обладающих высоким спектральным разрешением. В состав видеоспектрометров входят две системы. Во-первых, оптическая система, которая делит регистрируемую область пространства на набор смежных точек и, во-вторых, изображающий спектрометр, который разлагает состав принятого электромагнитного излучения на набор ограниченных спектральных полос. В результате видеоспектральной съёмки формируется многомерное пространственноспектральное изображение, в котором каждый элементарный участок изображения, «пиксел», характеризуется собственным спектром. Такое изображение носит название «куба» информации, два измерения которого соответствуют пространственному изображению местности на плоскости, а третье – характеризует спектральные свойства изображения. Спектральное разрешение современных видеоспектрометров достигает 1,8–2,0 нм и обеспечивает построение спектральных характеристик подстилающей поверхности, определяемой мгновенным полем зрения прибора (для авиационных видеоспектрометров – около 1 мрад).

Для решения конкретных задач используются гиперспектрометры различных типов – дисперсионные, фильтровые и интерференционные. В работах [5–31] приведены различные схемы гиперспектрометров, ис- пользуемых для дистанционного зондирования Земли. Большое количество задач может быть решено с помощью достаточно стандартных дисперсионных гиперспектрометров. В работах [7–10] представлено подробное описание компактного изображающего спектрометра (compact imaging spectrometer, COMIS), используемого в корейском микроспутнике STSAT3. Вес микроспутника составляет 150 кг при габаритах 85×82×100 см. Спутник, помимо спектрометра, также несёт многофункциональную систему инфракрасного наблюдения MIRIS (Multi-purpose InfraRed Imaging System), предназначенную для съёмки Галактики в ИК-диапазоне.

В качестве диспергирующего элемента в спектрометре может использоваться как призма, так и дифракционная решётка. Очевидным преимуществом дифракционной решётки по сравнению с призмой является компактность. Изображающие спектрометры, содержащие в качестве диспергирующего элемента дифракционную решётку, как правило, основаны на конфигурации Оффнера или конфигурации Дайсона [7–31].

В работе рассмотрено моделирование гиперспектрометра, основанного на схеме Оффнера, в рамках геометрической оптики и выполнено сравнение диспергирующих характеристик схемы с использованием призмы и дифракционной решётки.

1. Математический аппарат, используемый при моделировании работы гиперспектрометра в рамках геометрической оптики

Для того что бы сформировать гиперспектральный куб [2, 3], изображения, полученные с помощью гиперспектральной аппаратуры, необходимо подвергнуть процедурам обработки, фильтрации. Для этого необходимо знание аппаратных функций различного уровня, в частности функции рассеяния точки. В случае гиперспектральной аппаратуры точка на изображении прекращается в линию, каждая точка которой содержит информацию о спектральной характеристике.

Для того чтобы рассчитать распределение интенсивности в области фокусировки, необходимо найти ход лучей в оптической системе. Гиперспектрометр состоит из телескопической части и гиперспектрального блока (рис. 1).

Схема спектрометра, основанного на схеме Офф-нера, состоит из трёх зеркал, входной щели, плоско- сти изображения (рис. 1). Входная щель расположена в плоскости, перпендикулярной к оси z, и проходит через центры кривизны всех трёх зеркал. Первое и третье зеркало имеют радиус кривизны R, второе зеркало имеет радиус кривизны R/2. Иногда конструктивно первое и третье зеркала выполнены в виде одного зеркала (рис. 1). Луч выходит из источника падает на первое зеркало, отражается и падает на решётку, расположенную на втором выпуклом сферическом зеркале. Далее, отражаясь от третьего зеркала, приходит в плоскость регистрации. Методы расчёта телескопической части описаны во многих работах, в частности [32]. Моделирование гиперспектрального блока является предметом настоящей работы.

.S '! ( U , V ) = S o ( U i , V i ) -

- 2 n i ( U i , V i ) I n ( U i , V i ) , S o ( U i , V i )

Подставляя выражения для направляющего вектора падающего пучка и вектора нормали, получим

uuu    uu

a- r ^- r i _?r i

^S i ^{( U} i , ^V i )- । .     . ^{- 2}

Г о ^- r i r i

r ₁

r ₀

-

r ₁

r i

V

1 r - r У

В этом случае лучевое преобразование имеет вид

uu                  uuu r (Ui, Vi,l) = ri (Ui, Vi) + Si (Ui, Vi)l.                          (i3)

Пересечение луча со второй сферой

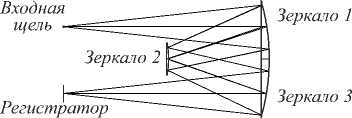
Рис. 1. Ход лучей в оптической системе

После отражения от первой сферы луч пересекает вторую сферу и отражается от неё. Обозначим уравнение второй поверхности

' ( r ) = о.

Для сферы с радиусом R / 2 уравнение приобрета-

Пересечение луча с первой сферой

Рассмотрим отражение луча от сферической поверхности x2 + y2 + z2 -R2 = 0.

Рассмотрим луч из точки с координатами x ₀, y ₀, 0 в точку u ₁, v ₁, Z , расположенную на поверхности первой сферы. Направляющий вектор имеет вид

- = S p_ = ( u i ^- x о ) i ⁺ ( ^V i ^- У 0 ) ^{j + Z} ( u i, ^V i ) k S ⁰     ^ ( u i ^- x о ) ^{2 +} ( V i ^- У о ) 2 ⁺ Z ² ( u i , ^V i )

uur    uuu

= r i ^- r o

=r - r> ( ui, Vi ) = uii+ Vi j

Г ( U i , V i ) = N ( U i , V i ) = U i i + V i j - Z i ( U i , V i ) k

ет вид

F2 (r ) = ( r, r)-RT = о.(i5)

Точка пересечения луча находится из условия

F2 (r (ui, Vi, l )) = о,(i6)

V)

Vri(Ui,Vi) + Si(Ui,Vi)li] - — = о.(i7)

Это уравнение сводится к квадратному

( R ²

l i ² + 2 V r i ( U i , V i ) , S i ( U i , V i ) ] l i + r ² ( U i , V i )—— = о. (i8)

Решая квадратное уравнение относительно l1 , получаем точку пересечения со второй сферой r2 = ri( Ui, Vi) + Si( Ui, Vi) li.                                     (i9)

Координаты ( u ₂ , v ₂) точки пересечения со второй

S о ( ^u p ^V i ) = V( u i ^- x о ) 2 ⁺ ( ^V i ^- x о ) 2 ⁺ Z ² ( ^u 1 ^{, V} i ) .        ⁽⁴⁾

Вектор нормали имеет вид

N ( U i , V i ) = r ( U i , V i ) = U i i + V i j - Z i ( U i , V i ) k .          (5)

Нормированный вектор имеет вид

х   N (ui, Vi ) ni (Ui, Vi )= АГ/ Г N(ui, Vi ) (6) ri (Ui, Vi) = N (Ui, Vi) = ^Ui2 + Vi2 + Z2 (Ui, Vi). (7) Закон отражения в векторной форме имеет вид [nix So ] = [ «iX s ], (8) Z!i X [ ^ X So ] = ^ X [ nxX Si ] , (9) n ^ n, So ^ - So = n V n, Si ^ - Si . (10) Вектор отражённого луча имеет вид сферой имеют вид uuuuu      uuuu                  uuuuu

( ^U 2 , ^V 2 ) = r 2 ± = r i ± ( ^U P ^V i )^{+ S} i ± ( u i , ^V i ) l i .

После отражения от второй сферы вектор направляющего луча имеет вид uuu                    uuu

S 2 (U 2, V 2 ) = Si (Ui, vi)- uuuu                 uuuu                uuu

- 2 n 2 ( U 2 , V 2 ) I n 2 ( U 2 , V 2 ) , S i ( U i , V i )

n ₂ ( и ₂ , v ₂) - нормаль ко второй сфере в точке пересечения луча, отражённого от первой поверхности в точке ( и ₂ , V ₂), со второй сферой. При наличии на второй сфере дифракционной решётки имеется несколько отражённых лучей. Дифракционная решётка представляет собой частный случай дифракционного оптического элемента (ДОЭ) на криволинейной поверхности В разделе 2 изложена общая теория дифракции света на ДОЭ на криволинейной поверхности.

Пересечение луча с третьей сферой

После отражения от второй сферы луч пересекает третью сферу и отражается от неё. Уравнение луча, отражённого от второй сферы, имеет вид

Гг = r1 (Uj, Vj) + 5^Uj, Vj) lj + 52 (и2, v2) l .(21)

Пересечение с третьей сферой с радиусом R определяется решением уравнения

Z _           __  X 2

I Tj (Uj, Vj) + 5j (Uj, Vj) lj + 52 (и2, v2) l21 - R2 = 0.(22)

женного на криволинейной поверхности в плоскости ( x , y ), отстоящей от начала координат на расстояние z .

Закон сохранения энергии имеет вид

I ( ^U j , ^V 1 ) • | ^TU ^X V • 1 ⁵ 0 ( ^U j , ^V 1 ) , n ( ^U j , ^V 1 ) J d ^U 1 d ^V 1 = = I ( x , y ) dx d y ,

( i X rout J J ^U 1, ^V 1 ) ,

Решая квадратное уравнение относительно l ₂, получаем точку пересечения с третьей сферой с радиусом R . Координаты ( и 3 , v 3 ) точки пересечения с

где l – расстояние от точки выхода луча до точки прихода луча, ^u S ^uuu ₂ – направление выходящего с по-

третьей сферой находятся по формуле uuuuu     uuuu

(U 3 , V3 ) = T3± = T1± (U1, Vj ) + uuuuu                      uuuuuu

+ 5 j _±( U j , V j ) l j + 5 2 _± ( U 2 , V 2 ) l 2 .

Вектор луча, отражённого от третьей сферы, имеет вид

верхности луча.

T ( u _j , v ₁) - коэффициент прохождения для луча, у которого точка пересечения с первой сферой имеет координаты ( и₁ , v ₁). Далее, используя свойство дельта-функции Дирака, можно записать выражение для освещённости в плоскости в виде

uuu                    uuu

5 3 (u 3 , V3 ) = 5 2 (u 2, V 2 )- uuuu                uuuu                uuu

- 2 n ( U 3 , V 3 ) I n 3 ( U 3 , V 3 ) , 5 2 ( U 2 , V 2 ) J ,

I ( ^T J = J 8 1 ^т _± ^- ( r out ] J ^U 1 , ^v j ) ] I о ( ^U 1 , ^v j ) х               (_3j)

X T ( U j , V j ) T u X г ( S 2 ( U j , V j ) • N )d U j d V j .

n ₃ ( u ₃ , v ₃) - нормаль к третьей сфере с радиусом R в точке пересечения луча, отражённого от второй поверхности в точке ( и ₃ , V ₃), с третьей сферой.

На практике при вычислении выражения (31) дельта-функция Дирака заменяется следующей аппроксимацией:

Пересечение луча с выходной плоскостью

Z x² + y²

8 ( x , y ) = a exp I---—

I      O '

.

После отражения от третьей сферы луч пересекает выходную плоскость. Уравнение луча, отражённого от третьей сферы, имеет вид

T = тД U j , V j ) + 5 j ( U j , V j ) l j + + 5 2 ( и ₂ , V ₂ ) l ₂ + 5 3 ( U 3 , V 3 ) l .

Пересечение с выходной плоскостью определяется уравнением

2. Асимптотические методы расчёта когерентного поля от ДОЭ на криволинейной поверхности в рамках скалярной теории

Рассмотрим дифракцию на ДОЭ на криволинейной поверхности, который обладает зонной структурой. Рассмотрим криволинейную поверхность, на которую нанесён дифракционный микрорельеф. Пусть поверхность описывается параметрическими уравнениями

( ^T 1 ( ^u 1 , ^v 1 ) ^{+ 5} 1 ( ^U 1 , ^v 1 ) l j ⁺

+ 5 2 ( и ₂ , v ₂ ) 1 ₂ + 5 3 ( и ₃ , v ₃ ) 1 ₃ , m ) = 0.

Решая уравнение относительно l ₃, получаем точку пересечения с выходной плоскостью

uuuuu      uu                  uuu rout = T1 (Uj, V1 ) + 51 (Uj, V1 ) lj +

+ 5 2 ( и ₂ , V ₂ ) 1 ₂ + 5 3 ( U 3 , V 3 ) 1 3 .

Так как (и2, v2) и (и3, v3) зависят от координат точки пересечения луча с первой сферой, то координаты точки пересечения с выходной плоскостью зависят только от них uuuuu      uuuuu rout = rout (Uj, V1 ) .                                                   (28)

Вычисление освещённости в рамках геометро-оптического подхода

В данном пункте настоящей работы рассмотрим вычисление поля от оптического элемента, располо-

x = x ( U , V ), y = y ^{( U} , ^V ), z = z ( и , V ).

Введём в окрестности поверхности криволинейные координаты x = X2(и, v) = x (и, v) + Nxt,(34)

y = Y2(u,v) = y (и,v) + Nyt,(35)

z = Z 2( и, v ) = z (и, v ) + Nzt.(36)

Пусть диэлектрическая проницаемость в окрестности поверхности задаётся в виде

e ( и , v , t ) = ^ g_n ( t ) exp ( ikn ф ( и , v ) ) , k = 2 ^ , n                       ^

где λ – длина волны. Физический смысл функции ф ( и , v ) в ряде случаев совпадает с функцией эйконала дифракционного оптического элемента.

Расчёт локального периода ДОЭ на криволинейной поверхности

Пусть поверхность и функция эйконала на поверхности описывается параметрическими уравнениями

Найдём теперь, как должны изменяться приращения d и , d v при изменении положения точки на поверхности вдоль вектора b ^r ₁ на расстояние d l : uuuu

г = г ( и , v ), ф = ф ( и , v ).

Рассмотрим кривую на поверхности, описываемую уравнением r      ur г (t) = г (и (t), v (t)).                                      (39)

Найдём на поверхности направление, вдоль которого функция не изменяется. Это направление находится из условия, которое в векторной форме можно написать в виде

uur d г -г     d и -г     dv

,d7= ^{г (} u • ^v *57^{+ г (} u • ^{v )}5 7' ф и ( и • v ’d u + ф v ( и • v ’d ^ = 0.

L           d t             d t

Выражаем d v /d t из второго

уравнения и, под-

ставляя в первое, получаем выражение для направления касательного вектора вдоль кривой

rr

r ⁽ t ) = r ⁽ u ⁽ t ’ • ^{v (} t )),                                       ⁽⁴¹⁾

d г d t

¹ d и ■■" ( ф v ⁽ u • ^v ’ ) "d^ ^B3 ,

где вектор B 3 = ф _v ( и • v ) г„ ( и , v ) - ф „ ( и , v ) г„ ( и , v ).     (43)

Вектор B ₃ имеет то же самое направление, что и касательный вектор к данной кривой.

Обозначим единичный вектор вдоль этого направления b₃

uuur b3 (и, v ) =

B 3 ( и , v )

B ₃ ( и , v )

Найдём направление, вдоль которого функция изменяется наиболее быстро. Это направление перпендикулярно вектору b₃ и вектору нормали к поверхности N :

uuuu b=т

Bi

В₃ ( и , v ) = [ B ₃ ( и , v ) х N ( и , v ) ], N ( ^и , ^v ) = [ и ^{( и} • ^v ) ^х г ^{( и} • ^v ) ] . Используя формулу векторной алгебры [ а х [ b х c ]] = b ( ac ) - c ( ab ),

uuu                 uuu                 B г (и, v) d и + г (и, v )d v = — dl.

.B i

Умножая векторное уравнение скалярно по очереди на Г ( и • v ), Г ( и , v ), получаем систему линейных уравнений

( ^ги ⁽ и • ^v ’ U ^{( и} • ^v ’ ) ^{d и +} ( v ^{( и} • ^v ’ U ^{( и} • ^v ’ ) ^{d v} =

_ ( B ^г„ ^{( u} • ^v ’ ) d l

=      B i         ,

( г„ ( и • v ) г„ ( и • v ) ) d и + ( г ( и • v ) г„ ( и , v ) ) d v =

_ ( B ^г, ^{( u} • ^v ) ) .

Bi где (B1 L 1 =фи (u • v’D ,

⁽ B l v ¹ = ф v ( и • v ) D ,

D = N ² = ( ^ l ( ^и • ^v ) • и ( ^и • ^v ) )( г ( ^и • ^v ) • v ( ^и • ^v

^- ( ^г ;( u • ^v ) • ^ги ( u • ^v ) ) ².

Решая систему линейных уравнений, получаем

d и =

ф и ^{( и} • ^v ’ (^ ; ( ^и • ^v )• ^ ; ( ^и • ^v ) )

B 1

V ф v(и •v ’ (г„(,и •v )• гД и •v))

d v =

B 1

t d l ,

Ф v ^{( и} • ^v ’ ( ^ги ( ^и • ^v )• ^" и ( ^и • ^v ) )

B 1

V фи(и •v ’ (^и(и •v )• г;(и •v)) '

--------------------------------------1 d l .

B 1

Подставляя выражения для d и , d v в выражение для изменения функции ф ( и , v ) на 2 п

2n ф и (и • v )d и + Ф v (и • v )d v = -—, k где k - волновое число, получим выражение кального периода дифракционной решётки

для ло-

получим выражение

(      (        "  1           (        "  11    "

B1 ( u, v ) = | фи (г, • г, 1 - Ф v (ги • г, Ц ги +

— Ф I г ,г ^ф и I и • v

2 n N d l =---- kB 3

.

(   (—   1

+ I Ф I г ,г I

I ф v I и • и I

) ₃     .

I ^гv .

В дальнейшем локальный период будем чать через d .

обозна-

Расчёт направления отражённых и преломлённых лучей при дифракции на ДОЭ на криволинейной поверхности

Найдём теперь изменение направления луча, преломлённого на криволинейной поверхности, на которую нанесён дифракционный микрорельеф. Пусть поверхность является поверхностью раздела двух сред с диэлектрическими проницаемостями £1, £2. Пусть луч падает со стороны поверхности с диэлектрической проницаемостью £1. Его направление описывается вектором S1. Отражён-uuuuuuur ные лучи имеют направление S1(n) . Лучи, преломлённые uuuuuuur на поверхности, имеют направления S2(n) .

Направления преломлённых лучей удовлетворяют следующим соотношениям:

[ S^, b J = [ S JR , b J + ( 2 n n )/( kd b£ ) , ^uuuuuuur uuur        uuuur uuur

. [ S 2 " ’ , b 3 J = ( S 2 , b 3 J ,                                      (57)

( S 2 " ) , S J ) = 1. uuuuuuur

Направления вектора S ₂ = S 20) и связаны с вектором падающего луча ^u S ^uu ₁ ^ur законом преломления.

Направления отражённых лучей удовлетворяют следующим соотношениям:

[ S t b J = ( S R , b J + ( 2 n n )/( kd £b ) , ^uuuuuuur uuur        uuuu  uuur

■ R S ' " ’ , b 3 J = R S 1 , b 3 J ,                                      (58)

( S ^- ") , S t ) = 1.

Здесь n – номер луча. ^u S ^uu ₁ ^ur связан с направлением падающего луча законом отражения. Для нахождения направления лучей, отражённых и прошедших через границу двух сред, на которой находится ДОЭ, необходимо знать направление падающего луча.

Пусть эйконал ф0 (u, v) в среде с диэлектрической проницаемостью £ задан на поверхности, описываемой параметрическими уравнениями r = R( u, v), Ф = ФО( u, v).

Найдём направление лучей, формируемых волновым фронтом с эйконалом ф ⁰ ( u , v ). Направление распространения луча можно найти из решения системы уравнений

' (1 / ^) ф 0 ( u , v ) = R S , r J = S x X u + Sy u + SZ u ,

■ 1/ V£) ф 0 ( u , v ) = ( S , r ) = SX v + Sy v + SZ v , (60) ( S , S ) = 1.

Найдём разложение направляющего вектора луча по касательным и нормальным векторам к поверхности, на которой задан эйконал падающего поля u       uuu     uuu     r

^S = pr + qr + tn ,

p =    '■ [ ф U ( v v ^J -ф ⁰ ( u , v ^JJ =

DA ^£ 2^{1                  J}

= —-— ^Rф⁰Г — Ф⁰ r ^J r , TX Г l ^ф u v ^ф v u J v , D V £ 2

■ q = Аг ( -ф 0 ( r ) +ф 0 (■ • r ) )

D V ^£ 2

= ^ь^{-ф 0} r u ) r ,,

(S. S)-1, где

D ( u , v ) = N ² =

= ( r u ( ^u , ^v ) , ^ru (. ^u , ^v ) )( r-A ^u , ^v ) , r v ( ^u , ^v ) ) ^{-              (62)}

• ^- ( rA u , ^v ) , r u ( u , ^v ) ) 2 .

Из полученных выражений видно, что проекция направляющего вектора луча на касательную плоскость к поверхности, на которой задан эйконал, имеет вид

S R R = b ^- (D d T£ 2 ),                             (63)

B R = R ф 0 ( - v - v J -ф 0 ( - u , - v ]! r u R +

_R                                                     (64)

• ⁺ l Ф v 1 r u , r u J -Ф u 1 r u , r v JJ r v .

Закон преломления луча на дифракционном оптическом элементе имеет вид

S" = SR+-^^L bx = kd J£ uuuur 2                                                  (65)

• = S _J ^R + -^^ nB L, = S _J ^R + _ B ^.

kd A £ 2 B 1        ^/£ 2 D

Таким образом, получено выражение для направления преломлённого луча на дифракционном элементе, расположенном на криволинейной поверхности, которое в дальнейшем будет использовано для расчёта интенсивности в рамках геометрооптического подхода.

Вычисление освещённости в рамках геометро-оптического подхода

В данном пункте настоящей статьи рассмотрим вычисление поля в плоскости (X, y), отстоящей от начала координат на расстояние z% от оптического элемента, расположенного на криволинейной поверхности

I ( u , v ) • [ r_u х r_v R • ( S ( u , v ) , N ( u , v ) ) d u d v = x , y I d x d y ,

x = x ( u , v ) + S 2

y = y ( u , v ) + S 2 y

( z - z ( u , v ) )

S 2 ^z

( z - z ( u , v ) )

S 2 ^z

где l – расстояние от точки выхода луча до точки прихода луча, S ^r ₂ – направление выходящего с поверхности луча.

Закон сохранения энергии имеет вид

I (x, y) = J 8( x - x (u, v), y - y (u, V) )x x10 (u, v) T(u, v) |ru x rv (S2 (u, v) N) du dv.(68)

( z - z ( u , v ) )

x = x(u, v) + Sx7,

<         ( ’ ) 2        S2,

( z - z ( u , v ) )

y = y (u, v ) + Sy------,

S 2

где v – коэффициент пропускания на поверхности.

Расчёт локального периода для ДОЭ на сферической поверхности

В данном разделе рассмотрим расчёт локального периода для ДОЭ, расположенного на сферической поверхности. Частным случаем ДОЭ является дифракционная решётка на сферическом зеркале, которая используется в гиперспектрометре, основанном на схеме Оффнера. Решётка не имеет радиальной симметрии. В этом случае параметрическое уравнение поверхности и фазовая функция дифракционной решётки имеют следующий вид:

x = u ,

J = ^v , z =

, 2

- u - v ,

ф = ф ( u ).

Следует отметить, что параметры u , v представляют собой декартовые координаты точки на сфере. Вектора

—►

—►

b i ( u , v ) =

B i ( u , v ) B i (u , v ) ,

B1 ( u , v ) = I B ₃( u , v ) x N ( u , v^

uuuu                        uuu  uuu  uuu            uuu  uuu  uuu

^B i^{( u} , ^v ) = Ф u \ ^rv , r v J r u ^- Ф u I Г ,, r v J ^rv .

B 1 ( u , v ) = N ( u , v ) B ₃( u , v ),

uuuu                        uuu  uuu  uuu            uuu  uuu  uuu

^B i^{( u} , ^v ) = Ф u I r v , r v J r u ^- Ф u I r u , r v J ^rv .

Выражение для локального периода имеет вид

2 n N ( u , v ) d =----------- .

kB ₃( u , v )

R ( u , v ), R ( u , v ) имеют вид

uuu

^ru ^{( u} , ^v ) = 1 , V

0 ,

u

uuu

^^^^^^e

z ( u , v ) ^J ,

Формулы, полученные в предыдущих разделах, позволяют вычислить направление лучей, отражённых от выпуклого зеркала в схеме Оффнера. Расчёты лучей, отражённых от первого и третьего зеркал, остаются неизменными. Вид формулы для интенсивности лучей, пришедших в точку, также остаётся без изменений.

Приведённый метод имеет существенный недостаток, заключающийся в том, что в рамках геометрической оптики мы не можем вычислить интенсивность луча, отражённого от дифракционной решётки. Коэффициент отражения может быть вычислен только в рамках волновой теории, а в некоторых случаях – только в рамках векторной электромагнитной теории [33].

Расчёт формирования изображения в схеме Оффнера с призмой с использованием программного продукта Zemax

В работе [7] была рассмотрена схема Оффнера с призмами, привёденная на рис. 2. В левой части схемы располагается телескопический блок с фокусным расстоянием 300 мм, в правой части располагается блок с диспергирующими элементами в виде двух призм P ₁ и P ₂ из кварцевого стекла. Также в правой части имеются три сферических зеркала M 1 , M 2 и M 3 с радиусами – 161,3 мм; –74,9 мм и –153,5 мм соответственно. Изображение регистрируется в плоскости детектора D.

Г ^{( u} , ^v ) = 0 1 , V

v

^^^^^^e

z (u, v) 7

Вектор нормали к сфере с радиусом R при данной параметризации поверхности имеет вид

N ^{( u} , ^v ) = ^ ^ru ^{( u} , ^v ) ^{x r}v ^{( u} , ^v ) ] =

u

v

^ z ( u , v ) , z ( u , v )

)

, 1 .

uuu      B             uuuu

Вектор b₃ = —, где B₃ имеет вид

³ B 3           ³

uuu

uuuu

uuuu

uuuu

uuu

^B 3^{( u} , ^v ) = ^- ф „ ^{( u} , ^v ) ^rv ^{( u} , ^v ).

Найдём направление наиболее быстрого возрастания функции. Это направление перпендикулярно век-

uuu

uu

тору b ₃ и вектору нормали к поверхности N .

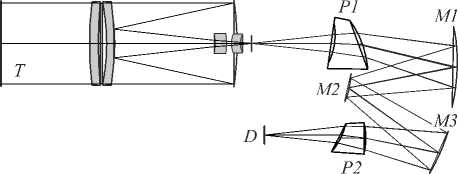
Рис. 2. Схема Оффнера с призмами

На рис. 3 и 4 приведены результаты моделирования такой схемы с использованием программного продукта Zemax [34].

Разброс спектральных порядков в плоскости регистрации диаметром 16 мм для различных длин волн приведён на рис. 3. Рассмотрен видимый диапазон длин волн (от 0,4 мкм до 1 мкм) и инфракрасный диапазон длин волн (от 1,6 мкм до 2,6 мкм).

На рис. 4 набор длин волн совпадает с набором, приведённым на рис. 3.

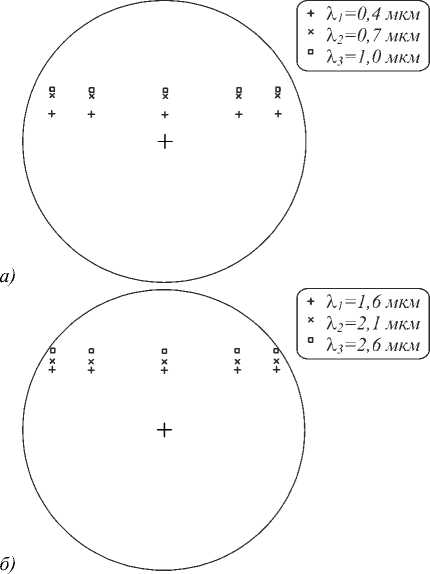
Рис. 3. Разброс спектральных порядков в плоскости регистрации для различных длин волн λ _i : для видимого диапазона (а); для инфракрасного диапазона (б)

^{б )}

Рис. 4. Формирование диспергированного изображения буквы F: для видимого диапазона (а); для инфракрасного диапазона (б)

Как видно из приведённых результатов, разброс спектральных порядков при использовании различных диапазонов длин волн существенно отличается. Для видимого диапазона наблюдается неравномерный разброс.

Формирование диспергированного изображения буквы F для различных диапазонов длин волн показано на рис. 4. Неравномерность разброса для видимого диапазона хорошо наблюдается и в этом случае.

Расчёт формирования изображения в схеме Оффнера с дифракционной решёткой

Схема Оффнера с дифракционной решёткой [7, 8], нанесённой на поверхность зеркала, приведена на рис. 5. В левой части схемы располагается телескопический блок с фокусным расстоянием 300 мм, в правой части располагается блок с двумя сферическими зеркалами M ₁ и M ₂, имеющими радиусы –159,6 мм и –80,6 мм соответственно, и диспергирующим элементом в виде дифракционной решётки, нанесённой на зеркало M ₂. Изображение регистрируется в плоскости детектора D.

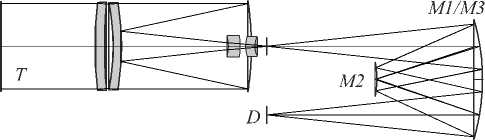
Рис. 5. Схема Оффнера с дифракционной решёткой

На рис. 6 и 7 приведены результаты моделирования такой схемы с использованием программного продукта Zemax.

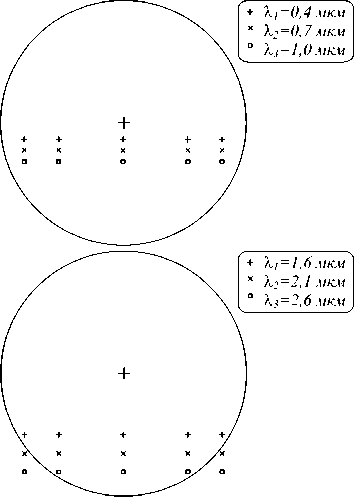
Рис. 6. Разброс спектральных порядков в плоскости регистрации для различных длин волн λ _i при использовании

дифракционной решётки: для видимого диапазона (а); для инфракрасного диапазона (б)

Рис. 7. Формирование диспергированного изображения буквы "F" при использовании дифракционной решётки:

для видимого диапазона (а); для инфракрасного диапазона (б)

Как видно из приведённых результатов, разброс спектральных порядков является равномерным для различных диапазонов длин волн. Это также является преимуществом (не считая облегчения веса) по сравнению с призмами, так как в этом случае облегчается обработка полученных изображений. Следует отметить, что разброс в инфракрасном диапазоне увеличивается. Эти факторы приводят к улучшению спектрального разрешения.

Формирование диспергированного изображения буквы "F" для различных диапазонов длин волн показано на рис. 7. Набор длин волн совпадает с набором, приведённым на рис. 6. Хорошо видна линейная зависимость разброса для различных диапазонов длин волн (видимого и инфракрасного) и увеличение разброса в инфракрасном диапазоне.

Заключение

В работе рассмотрен геометрооптический подход для моделирование гиперспектрометра, основанного на схеме Оффнера с призмами или дифракционной решёткой.

Показано, что использование дифракционной решётки вместо призмы не только облегчает общий вес оптической системы, но и приводит к более равномерному разбросу спектральных компонент диспергированного изображения.

Работа выполнена при поддержке Министерства образования и науки РФ и грантов РФФИ №№13-07-12181 и 14-07-97008.