Моделирование работы горизонтальных скважин в условиях неоднородности распределения свойств пласта

Множество математических моделей было построено и использовано для описания работы горизонтального ствола (Butler, 1994; Joshi, 1991). В настоящее время под математическим моделированием понимают чаще всего моделирование резервуара и скважины в гидродинамическом симуляторе. Однако данное описание системы скважина-пласт является, с одной стороны, слишком простым для описания реальной природы в силу дискретности и ряда модельных предположений, с другой – слишком сложным для принятия повседневных решений.

В силу значительной длины (> 1 км) горизонтальные скважины в ряде случаев пересекают пропластки с принципиально различными фильтрационно-емкостными свойствами. Кроме того, к горизонтальному стволу возможен приток многофазного флюида (смеси нефти, газа и воды). В процессе бурения каждой горизонтальной скважины по мере получения результатов интерпретации геофизических исследований в скважине стоит задача прогнозирования распределения притока (Семенов и др., 2009). С помощью установки устройств управления притоком ICD (Inflow Control Device) становится возможным влиять на распределение притока к горизонтальному стволу.

Зачастую горизонтальные скважины используются для разработки тонких (мощностью всего несколько метров) нефтяных оторочек. Одним из интереснейших эффектов является ко

нусообразование газа при работе горизонтальных скважин. Прогнозирование времени прорыва газа, а также характеристик работы скважины после прорыва требует описания притока к горизонтальному стволу в условиях неоднородности фильтрационно-емкостных свойств коллектора.

Цели данной работы: разработка, формулировка, применение и исследование ряда математических моделей, позволяющих принимать практические решения на основе реальных данных. В качестве математической модели работы горизонтальной скважины мы будем понимать зависимость суммарного дебита каждого из флюидов со скважины Q = f ( a 1 ...a n ) . Если одним из параметров a выступает время, то модель будет нестационарной.

Стационарная модель горизонтального ствола

Для учета неоднородности притока к горизонтальному стволу (подтверждаемой результатами промыслово-геофизических исследований (Семенов и др., 2009; Семенов 2010)), предлагается решение для каждого сегмента горизонтального ствола скважины следующей системы уравнений:

/ = pi(x ) ■ ( ^Pe - ^Pf ( x ) ) .

*( ( x ) = q o ( x ) + q g ( x ) + q ( x ),                                                     (1)

P f ⁽ x) - P wf ⁽ x) = ^{а (} p , ^ dqx) + ^{e (} p , ^ ( dq^x) ) ; dx          V dx J

В системе (1) координатная ось OX направлена вдоль горизонтального ствола, q ( x ) - дебит с сегмента, P_res – пластовое давление, P_s f – давление на границе фильтр-порода, P_w f – забойное давление, pi - коэффициент продуктивности на единицу длины, а(р, р) и в(р, р) — коэффициенты сопротивления ICD потоку (функции плотности и вязкости флюида соответственно). Нижние индексы «o», «g» и «w» обозначают нефть, газ и воду соответственно. Первое уравнение системы (1) позволяет определить приток каждого из флюидов с сегмента. Второе определяет суммарный дебит скважинного флюида в пластовых условиях в горизонтальном стволе на данном сегменте. Третье определяет дополнительный перепад давления, который оказывает фильтр или устройство управления притока на границе фильтр-порода.

Алгоритм решения приведенной выше системы уравнений является итерационным для каждого сегмента (первый сегмент выбирается у носка скважины и дальше к пятке). На первом шаге прогнозируется приток пластовых флюидов исходя из известного распределения коэффициента продуктивности pi ( x ) в начальном приближении P sf ( x ) = P wf ( x ). Затем рассчитывается общий приток многофазного флюида q ( x ) с сегмента. Исходя из дебитов различных флюидов вычисляются коэффициенты сопротивления притоку α и β для устройства по управлению притоком (они функции вязкости и плотности флюида). Затем вычисляется перепад давления на границе фильтр-порода P sf ( x ) - P wf ( x ), и для истинного значения P sf ( x ) рассчитывается приток флюида с сегмента. Таким образом, вычисляется приток с одного сегмента.

По мнению некоторых авторов (Антоненко и др., 2007), существенный эффект на приток оказывает перепад давления на трение в горизонтальном стволе (при работе на депрессиях, сравнимых с перепадом давления на трение), который предлагается учитывать для сегмента с помощью уравнения dPwf (x)   fMρ 2

= ₂₅ q ( x ), dx π r_s ⁵

где f M – коэффициент трения Муди, ρ – плотность, r s – внутренний диаметр трубы.

Тогда после вычисления притока с одного сегмента рассчитывается забойное давление для следующего сегмента, который расположен ближе к пятке (началу) скважины, чем предыдущий. Приток с каждого предыдущего сегмента добавляется к следующему, в результате чего получаются функции распределения q o ( x ), q g ( x ), q w ( x ) притока по длине горизонтального ствола.

Влияние устройств управления притоком

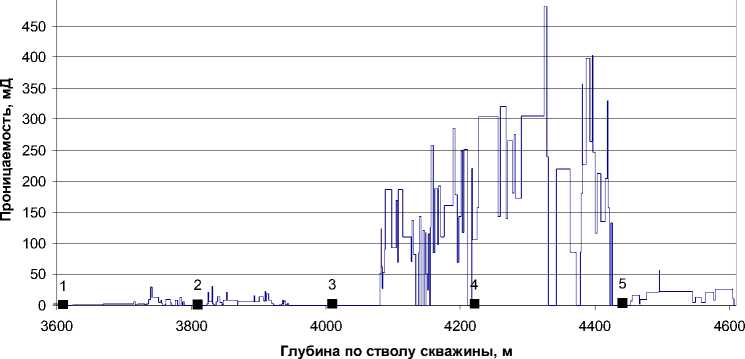
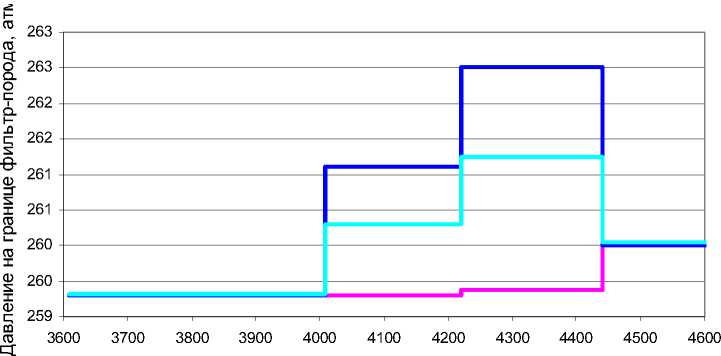
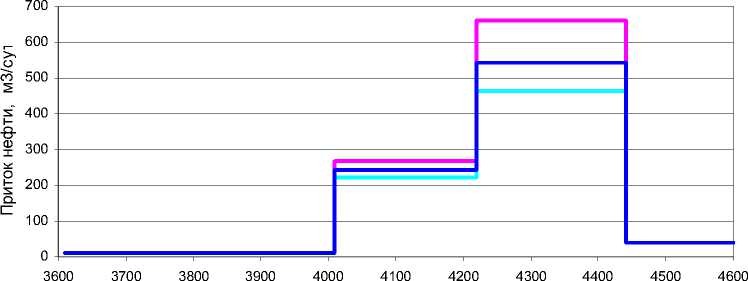
С использованием стационарной математической модели можно оценивать эффективность различных систем заканчивания во время бурения. Исходными данными для такой оценки является распределение проницаемости k ( x ), получаемое по результатам интерпретации геофизических исследований в открытом стволе (рис. 1а). Исходя из профиля распределения проницаемости и насыщенности по горизонтальному стволу определяются распределения давления на границе фильтр-порода P f x ) (рис. 1b) и притока q o ( x ) (рис. 1с). Таким образом, становится возможным оценить распределение притока и общий дебит скважины с использованием ICD и без. Применение в наиболее проницаемых зонах дополнительного сопротивления приводит к снижению притока с них.

Так, на Ванкорском месторождении устройства пассивного (устанавливается фиксированное гидравлическое сопротивление на все время работы скважины) управления притоком используют для снижения притока газа со скважин, на которых прогнозировался прорыв. Из сравнения вариантов с использованием данных систем и без них, а также в предположении прорыва газа по наиболее высокопроницаемому пропластку получается снижение дебита газа на 0,6 млн ст. м3/сут при использовании данных систем на 24 скважинах. На 15 из них диагностированы прорывы газа из газовой шапки.

Нестационарная многофазная модель горизонтального ствола

Стационарная модель позволяет вычислить распределение притока по длине горизонталь- ного ствола для данного значения Pres

dP в предположении установившегося (----= 0) или псев- dt dP доустановившегося ( res dt

= const) притока. Объем дренирования скважины определяется ви дом функции pi(x). Таким образом, стационарная модель подразумевает знание распределения насыщенности поровой среды вдоль горизонтальной скважины. В реальности насыщенность изменяется со временем в силу конусообразования.

Для моделирования движения газонефтяного контакта воспользуемся уравнением Dupuit-Forchheimer

a

b

Прот ив опесочный фильт р ICD соштуцерами ICD с винтовым каналом

c

Прот ив опесочный фильт р ICD сошт уцерами ICD с винтовым каналом

Рис.1. Распределение: a – проницаемости (цифрами показаны границы сегментов); b – давления на границе фильтр-порода; c – притока в горизонтальном стволе

дh     д f, дh^

= а I hI

д t    дy ( дy J с граничными условиями (Konieczek)

л » 5h (t-0)

q o             ⁸ У   .                                                            (4)

'=° uy

В уравнениях (3) и (4): h - высота контакта над скважиной, у - координатная ось перпен- л     (Ро - pg)kog                  л                                     „ дикулярно скважине, а =------5--скорость движения газонефтяного контакта, ф - по-

ИоФ ристость, rd – радиус горизонтального ствола.

Тогда если считать депрессию на пласт Ap (x) = Psf (x) - Pwf (x) переменной величиной на разных участках горизонтальной скважины, то дебиты нефти и газа на единицу длины скважины можно выразить как qo ( ,) = pio (x ).(1 - «x )2 )ap ( x )

q g ⁽ x ) = pi g ⁽ g ) 5 ⁽ x ⁾² a p ( x )

, - (x) - h (t, x,0)   .             „             ж                                    _ где o(t, x) = —------------ - безразмерный уровень нефти в горизонтальном стволе, zw(x) - d координата верхней части ствола скважины.

В таком случае qg(x) = pig(x)J2 2 = y(x) -^2-. qo(x) pio(x) (1 5 )        (15 )

Проинтегрировав удельные дебиты нефти и газа вдоль горизонтального ствола, можно получить следующее соотношение:

Q g

Q o

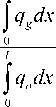
Г 5 2 &.p ( x ) dx

PI

PI^{gl 0}

o J ( 1 - ⁵' ) 4 p ( x ) dx

= /^.

Общий дебит газа с учетом газа растворенного в нефти можно выразить как

Q g = Q o

f yl+] •

BB

V g 0 /

где R s – газосодержание при давлении насыщения, B – объемный фактор.

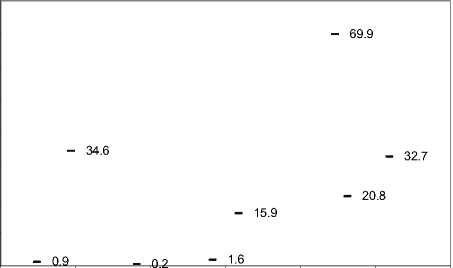
В (Mjaavatten et al., 2008) построена математическая модель на основе численного решения приведенных выше уравнений. Данная система уравнений разрешена относительно дебита – 433 – нефти в стандартных условиях в предположении, что дебит газа Qg известен. Основным допущением данной модели является однородность распределения свойств пласта вдоль ствола горизонтальной скважины. Как показано в (Семенов и др., 2009), в ряде случаев данное допущение неправомерно. Для учета неоднородности свойств мы предлагаем использовать вместо одной скорости движения газонефтяного контакта α ступенчатую функцию α(x) (рис. 2a).

Разрешать уравнение (7) будем относительно дебита газа, предполагая дебит нефти известным исходя из решения системы (1). Распределять общий дебит нефти по стволу можно также с помощью функции а( х) (рис. 2b). Уравнение (3) представляет собой нелинейное уравнение параболического типа, аналитическое решение которого возможно в силу автомодельности (Шапиро, 2005). Тогда зависимость h ( t , х , у ) можно задать в виде следующей рекуррентной формулы:

h i ( t i , x, У ) = h i - 1 + ^C ,2,2 ,                                                           ⁽⁸⁾

аф hi-i где C – постоянная интегрирования. Это и есть аналитическое решение уравнения (3).

a

80.0

70.0

60.0

50.0

ф

40.0

30.0

20.0

10.0

-

-           200         400         600         800        1,000       1,200

Расстояние от пятки скважины, м

b

0.0000450

0.0000400

0.0000350

0.0000300

0.0000250

0.0000200

CT

0.0000150

0.0000100

0.0000050

0.0000000

-           200        400        600         800        1,000       1,200

Расстояние от пятки скважины, м

Рис. 2. Распределение: a – скорости диффузии ГНК и b – удельного на единицу длины дебита нефти с течением времени (цифра-месяц)

Влияние устройств управления притоком с течением времени

Пусть устройство управления притоком создает на границе фильтр-порода на j-м участке горизонтального ствола перепад давления Ар1™, который является функцией удельного притока qj с данного сегмента длиной lj. Тогда закон сохранения массы для случаев эксплуатации скважины с ICD и без имеет вид mn

X ti X lj (qj- qC) ^ 0.

i = 1 j = 1

Если скважина без ICD работает с забойным давлением Pwf, то определим, каково должно ICD быть эквивалентное забойное давление Pwf , при котором функционал разницы добычи достигает своего минимума в предположении постоянства коэффициента продуктивности:

mn

X ь X l j q j l = 1 j = 1     ^

^- q j

P C —A P C

Pwf

= 0.

Тогда забойное давление P^ICD можно выразить как wf

P f = P , + ^1- 1 1. 1 q jj .                    (11)

¹¹ •Qi-¹

где й=1,А.

j ¹

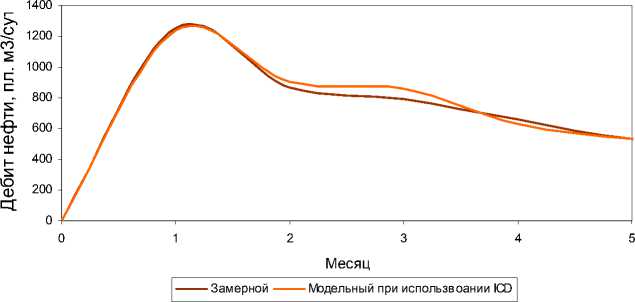
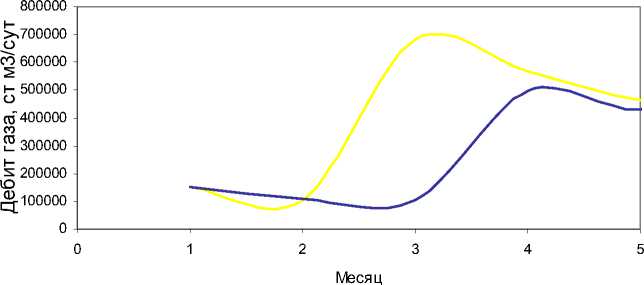
Забойное давление для режима работы скважины с установленным ICD выбирается таким образом, чтобы накопленная добыча нефти за время прогноза оставалась неизменной. Однако за счет более медленного движения газонефтяного контакта дебит газа со скважины снижается (рис. 3). Итак, за счет создания дополнительного сопротивления притока в наиболее высокопроницаемой части скважины удается увеличить время до прорыва газа на 1 мес.

Заключение

В работе представлены дифференциальные уравнения и системы уравнений, описывающие распределение притока многофазного флюида вдоль ствола горизонтальной скважины. Важным достоинством данных математических моделей является учет дополнительного перепада давления на границе фильтр-порода и неоднородности распределения фильтрационноемкостных свойств коллектора, которое имеет место на практике. Также принимается в расчет и перепад давления под действием силы трения вдоль горизонтального ствола при движении многофазного флюида по хвостовику. Приведено стационарное и нестационарное решение (в предположение движения газонефтяного контакта) задачи прогнозирования дебита нефти из горизонтальной скважины.

Показано влияние дополнительного гидравлического сопротивления на границе фильтр-порода (на практике реализуется в виде установки устройств управления притоком) на распределение притока. Наибольшее влияние данные устройства оказывают на приток из наиболее высокопроницаемых зон, приводя к снижению притока из них, а значит, и к уменьшению скорости движения газонефтяного контакта.

a

b

Дебит газа модельный ^^^^^^^е Дебит газа модельный при использов ании ICD

Рис. 3. Дебиты: a – нефти и b – газа

В предположении постоянства функционала накопленной добычи нефти со скважины отмечается снижение дебита газа со скважины при использовании устройств для управления притоком при малом изменении динамики дебита нефти.