Моделирование работы электронного измерителя механического момента электрических машин в системах автоматического управления

Многими исследователями предпринимаются попытки использовать электрические машины, входящие в состав различных электротехнических комплексов и систем не только в качестве электропривода, но и в качестве измерителей различных физических величин, информация о которых необходима при функционировании той или иной системы. В работе рассмотрена возможность определения механического момента с погрешностью 0,5-3 % путем разработки и использования оптимальных алгоритмов учета энергетических преобразований в электрической машине, реализация которых возможна при использовании аналого-цифровой и вычислительной техники. Этот метод базируется на контроле за энергетическими преобразованиями, происходящими в электрической машине [2] и ориентирован на применение в этих целях современных измерительных и вычислительных средств.

1. Принцип действия измерителя

Использование того или иного метода определения момента во многом определяется спецификой технологического процесса. Предлагаемый измеритель предназначен для более точного определения механического момента электрических машин по их собственным параметрам и независимым переменным. Такой подход для определения механического момента электрических машин в дальнейшем изложении будем называть энергетическим. Концепцию метода определения механического момента можно описать следующими уравнениями, которые следует рассматривать в контексте с решаемой задачей, как средство изложения решения [3]:

Р2=Р1±£Д7’;(1)

Р2 = соМ;

Л ±УАР

М= '      ',(3)

со

Волович Георгий Иосифович - д-р техн, наук, профессор кафедры радиотехнических систем ЮУрГУ;

Топольский Дмитрий Валерианович - канд. техн.

наук, доцент кафедры электротехники ЮУрГУ;

Volovich Georgy Iosifovich - PhD, professor of radio-technical systems department of SUSU;

Topolskaya Irina Iosifovna - assistant of electric devices

где со - угловая частота вращения, знак «+» соответствует генераторному режиму работы, знак «-» соответствует работе электрической машины в режиме двигателя.

Уравнение (3) является наиболее удобной математической моделью для физической реализации измерительного устройства. Это объясняется тем, что две наиболее весомых величины Р_х и со, входящие в уравнение (3), можно достаточно точно контролировать относительно простыми техническими средствами. Третья величина ^А^ составляет лишь малую часть общей мощности. Требования к точности определения данной величины менее жесткие, зависят от КПД электрической машины и существенно снижаются с ростом КПД. Следует учитывать, что при определении вращающего момента величина ^Д/, включает только те потери, которые имеют место в основном процессе преобразования энергии.

Мощность Р_х электрических машин целесообразно контролировать путем численного интегрирования мгновенной мощности:

• 1 ^N

A (4)

Px=^№-WY (5)

N t=i где uAB(JC), uBC(k), i^k), ic(k) - мгновенные значения линейных напряжений и токов трехфазной машины, соответствующих k-му измерению их на периоде Т с постоянным шагом TIN; N - количество измерений за период; ия(к) и ix(k) -мгновенные значения напряжения и тока якоря машины постоянного тока. Аналогично решается задача определения эффективных и средних значений токов и напряжений электрических машин. Например:

• У⁷* к=\

Применение программного метода контроля потерь мощности позволяет учесть их зависимость от параметров электрической машины:

ДРэл= cxf (1 + a (t-tH0M)) + Шщ1;(9)

^Ma™=C2^;(10)

^^мех- ®(c3 + C4CO),(11)

где IviU- линейные ток и напряжение трехфазной машины или ток якоря и напряжение обмотки возбуждения машины постоянного тока; t и /_ном - измеряемая температура и номинальная температура электрической машины; a - температурный коэффициент сопротивления; Д(/_щ - суммарное падение напряжения на переходах «щетка-коллектор»; С1...С4 - константы, посредством которых устройство адаптируется к конкретному типу электрической машины. В качестве таких констант приняты величины, определяемые традиционным путем проведения опытов холостого хода и короткого замыкания. Ориентировочные значения констант можно определить по основным данным электрических машин. Квадратичная аппроксимация в уравнениях (10) и (11) является компромиссным решением, упрощающим техническую реализацию устройства. Применение более точного описания магнитномеханических потерь мощности не исключено, но может оказаться малоэффективным вследствие отмеченного ранее фактора случайности.

Для машин постоянного тока формула определения вращающего момента имеет вид

М = Д f («я (к) • /я (к)) ± (сД f z2 (к) х Л к=1™ к=1

• *0 + «(^ЖН'ном)) ^U^^i_x(k)) +

• .           к=1

• 1    N/ 1

х(с3 +с4 -^Х®)))/— Ц^к), к=1         /к=1

где и_я (к), г, (к), о»_я (к), t(k) - мгновенные значения напряжения, тока, скорости вращения и температуры обмотки якоря машины постоянного тока соответственно, соответствующих ^-му измерению их на периоде Т с постоянным шагом TIN; N - количество измерений за период; и_в(к) - мгновенное значение напряжения обмотки возбуждения; /_ном - номинальная температура электрической машины; a - температурный коэффициент сопротивления; А1/_щ - суммарное падение напряжения на переходах «щетка-коллектор», С1...С4 - константы, посредством которых устройство адаптируется к конкретному типу электрической машины.

Для машин переменного тока вращающий момент определяется по формуле

1 N

^М = <^ <^uab W • i_A W - и_вс (к) • i_c (к)) ±

Л 4=1

±(^Е^(1 + «ДЬ^)-?ном)) + Л 4=1                4=1

1                                  к— 1

+Й®pW-fe +с4/^Z^W> (13)

4=1                                   / 'V 4=1

где и_АВ(к), и_вс(к), i_A(k), i_c(k) - мгновенные значения линейных напряжений и токов трехфазной машины соответственно; и^к"), i_n(k) — усредненные значения мгновенных значений линейных напряжений и токов; <о_р(к) - мгновенное значение скорости вращения ротора. Параметры интегрирования и все прочие обозначения в формуле (12) аналогичны рассмотренным в формуле (11). В формулах (11) и (12) в двигательном режиме работы вместо знака «±» следует подставлять знак «-», в генераторном режиме знак «+».

2. Описание модели и результаты моделирования

Учитывая, что механический момент является импульсной величиной, исследование динамических характеристик аналого-цифровых измерительных устройств, использующих при измерении механического момента энергетический подход, является важной задачей. Получение сведений такого характера во многом определяет возможность применения для конкретных целей подобных измерителей. Результаты этого исследования должны обеспечить возможность разработки систем, в состав которых входит подобное измерительное устройство.

Исследование проведено методом динамического моделирования для различных типовых режимов работы электрических машин. На основе анализа результатов динамического моделирования и известных методов исследования систем автоматического управления рассмотрена эквивалентная структурная схема измерителя (рис. 1).

Основной целью проведенного моделирования было сопоставление момента на валу электрической машины с моментом, измеренным аналогоцифровым устройством по разработанному алгоритму (см. рис. 1). Учитывая, что по сравнению с другими типами электрических машин наилучшими качествами с точки зрения регулирования обладают машины постоянного тока, для проверки работы электронного измерителя момента в динамическом режиме была выбрана математическая модель машины постоянного тока.

Собственная динамика измерительных устройств, работающих на вышеупомянутом принципе, была приведена в следующей постановке задачи. Каждый измерительный канал описан дифференциальным уравнением 2 порядка, что соответствует наличию в каждом канале линейного фильтра, где Т_и, Г₁₂, T₂i, Т₂₂, Т_зх, Т₃₂ - постоянные времени фильтров; Gn, G₁₂, G_2b G₂₂, G₃₁, G₃₂ - коэффициенты усиления фильтров; /ф, ^МФ> 'Уф “ отфильтрованные ток, напряжение и угловая скорость соответственно; уь у₂, у₃ - переменные состояния фильтров в каналах измерения тока, напряжения и угловой скорости якоря соответственно:

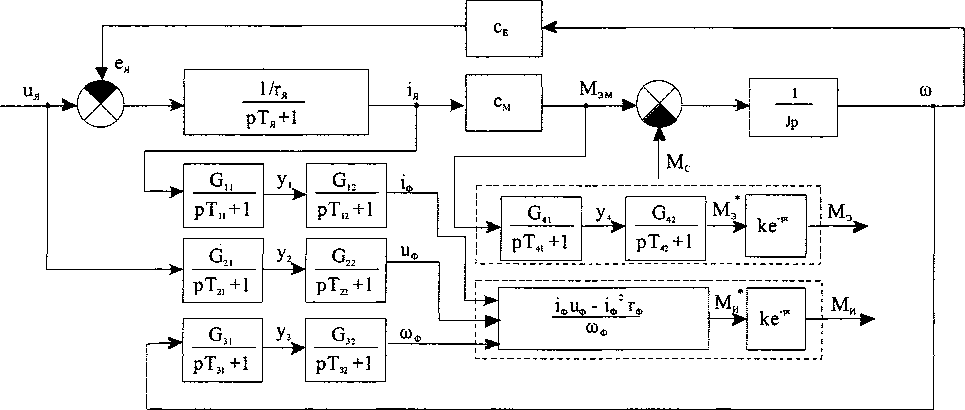
Рис. 1. Математическое описание динамической модели

*^1 _      ^11 ⁺ ^12 *Ф ] ^11^12

dt У' ТХХТХ2 ТХХТХ2 ТХХТХ2 я’

ние М_И при пуске двигателя при питании от управляемого выпрямителя. На рис. 4 показаны результаты измерения момента при пуске двигателя при питании от широтно-импульсного преобразователя.

^2 _     ^21 ⁺ ^22 ^МФ ! ^21^22 _ц

• 7,              гр гр       гр гр      гр гр     Я ’

at        ^2^22   ^21^22   ^2V22

—- = y₂, dt ²

^3 _     ^31⁺^32 ®Ф ! ^31^32

dt 3 T3XT32 T3XT32 T3XT32

d®^                            ■

""ЗГ-Уз-                           ■ dt

Наличие цифрового вычислительного устройства в измерителе вращающего момента обуславливает дискретный характер его работы. Входными сигналами данного цифрового звена являются ток /ф , напряжение Ыф и угловая скорость вращения Оф электрической машины. Переменная М* является результатом вычисления момента по нелинейному алгоритму, без учета дискретности измерителя. На вычисление требуется некоторое время т . Выходным сигналом измерителя являет-

u

в)

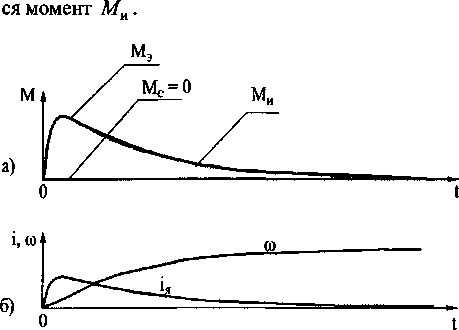
Рис. 2. Реакция системы при пуске двигателя от идеального источника постоянного напряжения

В процессе исследования показания измерителя М_И сравнивались со значением электромагнитного момента М_эм в различных ситуациях: пуск двигателя от идеального источника постоянного напряжения, управляемого выпрямителя или широтно-импульсного модулятора, а также реакция системы на скачкообразное изменение М_с. Данные, полученные при пуске двигателя от идеального источника постоянного напряжения, представлены на рис. 2. Рис. 3 демонстрирует измере-

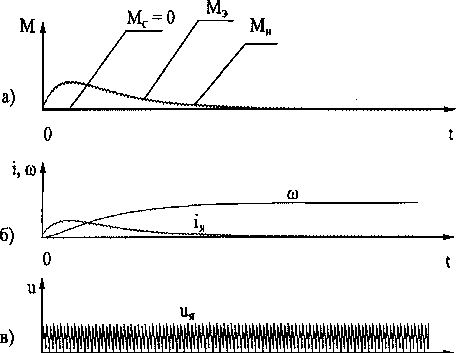
Рис. 3. Реакция системы при пуске двигателя при питании от управляемого выпрямителя

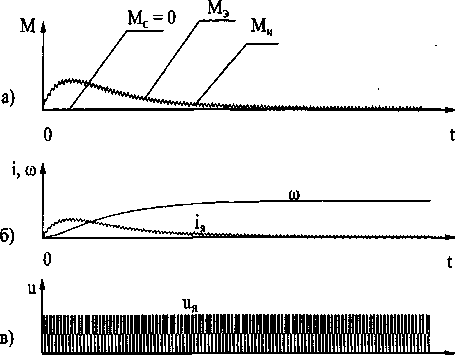
Рис. 4. Реакция системы при пуске двигателя при питании от широтно-импульсного модулятора

Результаты реакции рассматриваемой системы на скачкообразное изменение М_с приведены на рис. 5. Рис. 5, а соответствует идеальному источнику питания, рис. 5,6 демонстрирует случай с питанием от управляемого выпрямителя, а рис. 5, в случай с широтно-импульсным преобразователем.

Эквивалентное значение измеренного момента М₃ получено путем преобразования значения электромагнитного момента М_эм, которое на цифровой модели может быть определено точно.

Рис. 5. Сравнение результатов определения вращающего момента по разработанному алгоритму и по эквивалентной функции при скачкообразном изменении нагрузки

Заключение

В ходе моделирования была исследована динамика цифрового измерителя момента с учетом источника питания. Задача исследования классифицирована как исследование динамики нелинейной цифровой системы, включающей нескольких параллельных каналов для измерения аналоговых сигналов.

Исследование выполнено методом динамического моделирования первого типа [1] на основе численных методов для типовых случаев изменения вращающего момента на валу электрической машины: при изменении момента сопротивления и при пуске. Собственная динамика измерительных устройств, работающих на вышеупомянутом принципе, была приведена в следующей постановке задачи. Каждый измерительный канал описан дифференциальным уравнением 2 порядка, что соответствует наличию в каждом канале линейного фильтра. Динамические сигналы обрабатываются в соответствии с разработанным нелинейным алгоритмом. Значения показаний измерителя сравнивались с электромагнитным моментом. Результаты исследования показали, что измеренный момент отличаются от электромагнитного в пределах точности, предъявляемой к ряду испытательных стендов (0,5-3 %), а также что скорость изменения измеренного момента соответствует скорости изменения входных параметров измерителя. Кроме того учтена дискретность, характеризуемая временем, затрачиваемым на вычисления. По результатам проведенного исследования разработана эквивалентная линейная передаточная функция измерителя и разработана методика расчета коэффициентов.