Моделирование работы пневмотранспорта в импульсно-поршневом режиме

Пневмотранспорт позволяет экономить не только рабочие площади, но и финансы на оплату физического труда. К нему выдвинуты строгие требования. Пневмотранспорт для сыпучих материалов должен быть гигиеничным. Его использование сокращает потери сырья при транспортировке [1 – 5].

Расчет пневмотранспорта осуществляется на основании физических и химических характеристик транспортируемого ма- териала. Во внимание берут размер гранул, удельный вес, влажность сырья, его структуру, форму частиц.

Также необходимо определить нужную производительность оборудования, которая зависит от его мощности. После того, как расчет пневмотранспорта сыпучих материалов готов, составляют эскиз будущей конструкции. С его помощью можно определить «слабые» места установки.

В этом процессе просчитывают потери давления в самой системе. На основании этих расчетов выбирают вид загрузочного агрегата и его мощность.

В нагнетательном виде установок перемещение материалов осуществляется под воздействием воздушных потоков. Конструкция оборудования представлена проводом для транспортировки материала, осадителем с фильтрами, воздухопроводом и побудителем тяги. В качестве последних конструкционных элементов используют воздуходувки.

Оборудование нагнетательного типа характеризуется образованием избыточного давления во время работы. Это дает возможность использовать его для перемещения материалов на длинные расстояния, независимо от концентрации смеси. К этой категории относят системы пневмотранспорта и аспирации мукомольных заводов.

Кроме существенных преимуществ, пневмотранспорт для цемента или другого сыпучего материала имеет несколько недостатков. К ним относят значительное потребление электрической энергии. В процессе транспортировки в некоторых случаях происходит дополнительное измельчение продукции. Также быстро выходят из строя трубопроводы. Чтобы такого не происходило, в создании установок используют износостойкие трубы для пневмотранспорта.

Пневмотранспорт для песка или другого сыпучего сырья может осуществляться контейнерами, воздуходувками, желобами. Выбор способа транспортировки зависит от типа материала.

Пневмотранспорт применяется в строительстве и на промышленных предприятиях, где необходимо транспортировать большое количество материала. Также ее используют в системах отопления.

Установки используют в таких отраслях промышленности как химическая, пищевая, фармакология, производство муки, зерноперерабатывающая.

Пневмотранспорт помогает выгружать и загружать контейнеры, цистерны и другие виды емкостей для транспортировки. С его помощью осуществляется подача сырья от одного производственного участка к другому.

Разновидностью этого вида транспорта является импульсно-поршневой транспорт. В этом режиме сплошной поток разделяется на отдельные поршни (длиной до 2 м) воздушными промежутками (рис. 1) [1 - 5].

Данные режимы могут быть задейство- дисперсных материалов. При эксплуатации таких установок требуется строгое выполнение предписанных параметров работы, иначе возможно забивание транспортного трубопровода.

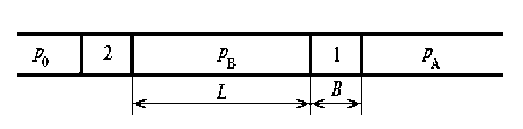
Рисунок 1 - Схема пневмотранспорта (1,2 движущиеся поршни)

Примем следующую физическую модель.

В начальный момент времени по горизонтальной трубе под действием перепада давлений Ap (0) = pо - pА начинает двигаться первый цилиндр. В момент, когда расстояние от входа в трубу до первого цилиндра достигает (Lо + B), в трубу добавляется второй цилиндр. Цилиндры имеют одинаковую массу m, длину B, диаметр D. Давление на входе ро и на выходера не изменяются (ро >рa).

Требуется найти, как будут изменяться скорости цилиндров, за какое время первый и второй цилиндр преодолеют заданное расстояние.

В работе принято 6 основных допущений.

• 1)    Диаметр цилиндра равен внутреннему диаметру трубы.

• 2)    Масса воздуха между цилиндрами не изменяется.

• 3)    Давление воздуха между цилиндрами p B изменяется изотермически:

Р в (0) • V (0) = Р в ( t ) • V ( t ) ^

^ Р о • L о = Р в ⁽ t ) • L ⁽ t )•                      ⁽¹⁾

Сила сухого трения, действующая на цилиндр, определяется по закону Кулона:

F = f • m • g ,.                          (2)

где g - ускорение свободного падения;

f - коэффициент трения.

• 5)    Коэффициент трения покоя (сцепления) равен коэффициенту трения в движении f .

• 6)    Силой гидродинамического сопротивления можно пренебречь.

Математическое решение задачи разобьем на этапы.

Первый цилиндр до появления второго будет двигаться с постоянным ускорением:

а о = A p (0) • S / m - f • g , S = n D 2 /4 . (3)

ваны только для хорошо аэрируемых сыпучих

Откуда его скорость и координата на первом жтапе рассчитываются по известным формулам равноускоренного движения:

W1(t) = a0 • t , X 1(t) = a0 • t2/2 .(4)

Первый цилиндр достигнет координаты X 10 = L 0 + B за время t 0 :

t0 = д/2 • ( L 0 + B ) / a 0

и будет иметь в этот момент скорость W 10 :

W10 = 42 • (L 0 + B) • a 0 .(6)

После чего начинается второй этап движения.

В начале второго этапа p B = p ₀ , поэтому второй цилиндр остается неподвижным, тогда как первый продолжает движение. Из-за этого объем воздуха между цилиндрами будет увеличиваться, а его давление падать по формулу, следующей из (1):

p B ( t) = p ₀ • L ₀ / L ( t) = ...

... = p 0 • L 0/ (X i( t) - B ).(7)

Второй цилиндр начнет движение лишь тогда, когда сила давления возрастет до величины силы трения:

(p0 - pB(t)) • S ^ f • g • m .

Подставляя (7) в (8) получим координату завершения 2-го этапа:

X11 = ---—--L 0 + B .(9)

p 0 ^{S -} fgm

До этой координаты динамика первого цилиндра определяется уравнением:

d W 1

m       = (pb (t) - pa ) • S - f • g • m .

dt

Подставим (7) в (10) и от аргумента t (время) перейдем к аргументу X (координата)

^W 1

d W 1

dX

f p 0L 0       )

I              - ^p A I •

< X - B     )

- f • g . (11)

Начальные условия к (11):

X (10) = B + L0 , W (10) = W10 .(12)

Первый интеграл дифференциального уравнения (10) находится аналитически

W 1 = ф ( X ) = W 10 + 2 / p⁰^- h ^f X—B \ [ m I ^L 0 ^J

Третий этап начнется, когда будет вы-полено условие (8), и начнется движения второго цилиндра. Запишем систему урвнения движения двух цилиндров d W 1

m ------= (pB(t) - pa ) • S - f • g • rn , dt dX

—1 = W i , dt

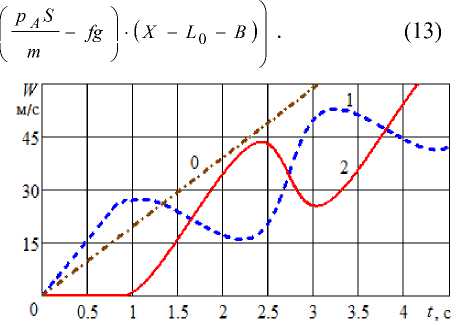
Рисунок 2 – Зависимость скорости цилиндров от времени: 1 – первого цилиндра, 2 – второго цилиндра; 0 – при совместном движении двух цилиндров

dW m------= (p0 - pB (t)) • S - f • g • m , dt dX

----- = W ₂ .

dt

p b ( t ) = L o / ( X i - X 2 + B ) .      (16)

Начальные условия к (14 – 16) при t = t 1 :

W 1 = Ф ( X 11 ) , X 1 = X 11 , W 2 = 0 ,

X 2 = 0 .                          (17)

На рис. 2 – 4 представлены результаты решения задачи численным методом при следующих значениях параметров: m = 20 кг; D = 0,1 м; L 0 = 10 м; B = 1 м; f = 0,8.

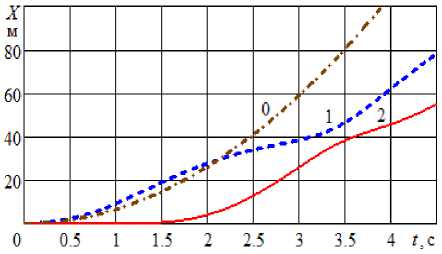
Рисунок 3 – Зависимость координаты от времени: 1 – первого цилиндра, 2 – второго цилиндра; 0 – при совместном движении двух

цилиндров

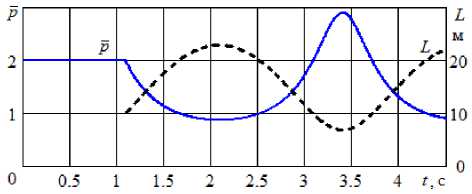
Рисунок 4 – Изменение безразмерного давления p = p_B / p _A и расстояния между цилиндрами по времени

На рис. 5 – 8 показано влияние величины L 0 на решения задачи. Остальные параметры не изменялись. По рис. 7 и 8 можно определить время, за которое цилиндр преодолеет заданное расстояние. Например, первый цилиндр в случае 1 пройдет 120 м за 6,1 сек, а второй и третий – примерно за 5,6 сек.

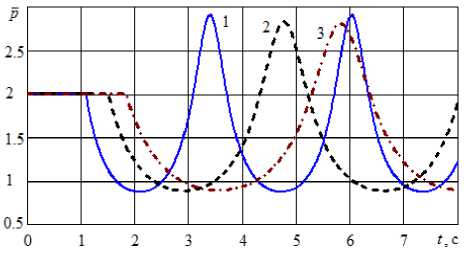
Рисунок 5 – Изменение безразмерного давления при различных начальных расстояниях между цилиндрами: 1 – L 0 = 10 м; 2 – L 0 = 20 м; 3 – L 0 = 30 м

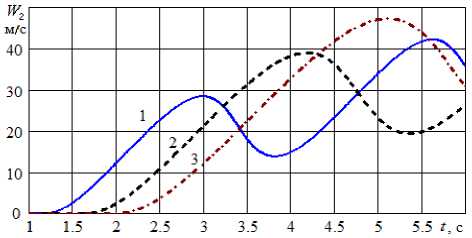
Рисунок 6 – Изменение скорости второго цилиндра при различных начальных расстояниях: 1 – L 0 = 10 м; 2 – L 0 = 20 м;

3 – L 0 = 30 м

Из рис. 7 – 8 следует, что изменение начального расстояния между цилиндрами незначительно влияет на время прохождения достаточно больших расстояний. Однако результат является следствием использования упро- щенной модели. В частности, по рис. 6 видно, что с увеличеним L0 заметно растет скорость, достигая 45 м/с. Тогда в реальном процессе будет сказываться действие силы аэролинамиче-ского сопротивления на цилиндры.

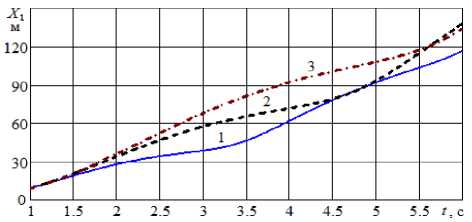
Рисунок 7 – Изменение координаты первого цилиндра при различных начальных расстояниях: 1 – L 0 = 10 м; 2 – L 0 = 20 м;

3 – L 0 = 30 м

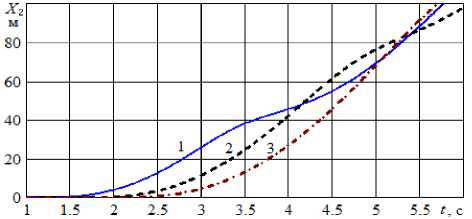
Рисунок 8 – Изменение координаты второго цилиндра при различных начальных расстояниях: 1 – L 0 = 10 м; 2 – L 0 = 20 м;

3 – L 0 = 30 м