Моделирование, расчет и мониторинг шума транспортных потоков

Тольяттинский государственный университет

Рассмотрены основные принципы моделирования и расчета шума транспортных потоков. Для моделирования улично-дорожных сетей выбран метод теории графов. Приводится описание программного обеспечения по составлению шумовых карт нового типа, с использованием которого построены шумовые карты г. Тольятти

В условиях современного города шум транспортных потоков воздействует на окружающую среду и человека наиболее интенсивно (60-80% от общей доли шумов, настигающих человека в жилой застройке), поэтому актуальным является его моделирование, расчет и прогнозирование. Необходимо не только пассивно констатировать всё увеличивающееся воздействие транспортного шума, но и грамотно оценить последствия проводимых мероприятий с использованием различных методов прогнозирования и оценки шума.

Шум автотранспортных потоков зависит от интенсивности движения и состава потока. Ориентировочно шум транспортного потока (дБА) в зависимости от интенсивности движения (I, автомобилей/ч) для больших интенсивностей 1000-5000 автомобилей/ ч можно оценить по формуле:

L_a = 72 + 10lg -I-

A ₁₀₀₀ . (1)

Зависимость уровня звука от интенсивности движения и состава потока [3] показана на рис. 1.

Распространение шума в застройке имеет отличия от распространения звука в свободном звуковом поле. Эти отличия объясняются в первую очередь наличием отражения от строений, звукопоглощением в зелёных насаждениях, дифракцией звука через различные сооружения, а также наличием реальных источников: например, линейных (транспортные потоки), плоских (стенки шумящих сооружений), точечных (заборные шахты вен- тиляционных установок, отдельные транспортные экипажи, трансформаторы, самолёты). Линейный источник создаёт цилиндрические звуковые волны, точечный – сферические, плоский – плоские звуковые волны. На большом расстоянии все источники звука являются источниками сферических звуковых волн. Граница перехода, например, цилиндрических волн в сферические (м) будет следующей:

F гр

где l - длина линейного источника, м.

Скорость звука зависит от температуры воздуха, при увеличении её на 1° скорость возрастает на 0,5 м/с. При наличии в воздухе слоев с разной температурой звуковые лучи преломляются и характер затухания звука с

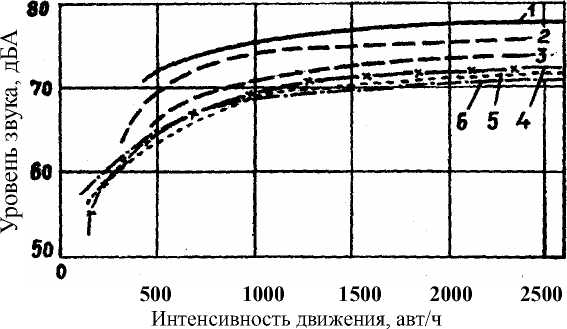
Рис. 1. Зависимость среднего уровня звука от интенсивности движения и состава потока: 1 – свыше 50% состава тяжелых автомобилей; 2 – 33-50%; 3 – 25-33%; 4 – 20-25%;

5 –15-20%; 6 – до 15 % расстоянием существенно изменяется. Поэтому в зимние морозные дни или в холодные весенние дни хорошо слышен звук на большие расстояния. Влияние ветра на распространение звука весьма велико, при встречном ветре эффект дополнительного снижения может достигать 20-25 дБ.

На степень затухания при распространении шума влияет состояние отражающей поверхности. Экспериментами показано, что при увеличении высоты распространения звука свыше 5 м это влияние снижается.

Для выполнения расчётов затухания звука от различных источников и в различных условиях можно воспользоваться данными экспериментальных исследований, приведёнными на рис. 2.

Распространение шума на территории жилой застройки - сложный процесс, характеризующийся такими явлениями, как расхождение (дивергенция) звуковых волн, наложение их (интерференция), огибание (дифракция), преломление (рефракция), отражение, рассеяние, поглощение элементами внешней среды и др. Эти явления должны учитываться при расчете звука. Транспортный поток можно представить в виде модели, состоящей из бесконечного числа некогерентных источников шума равной звуковой мощности, расположенных по одной прямой линии на одинаковом расстоянии один от другого. В общем случае, такой источник шума рассматривается как комплексный источник псевдоцилиндрических звуковых волн (уровень звукового давления которых снижается на каждое удвоение расстоя-

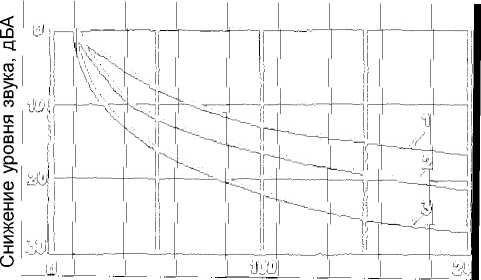
Расстояние от источника шума, м

Рис. 2. Снижение уровня звука над разными поверхностями от транспортного потока длиной 20 м: 1 - над асфальтом; 2 - над грунтом; 3 - над газоном ния в пределах от > 3 до < 6 дБ в зависимости от расстояния между источниками шума).

Дифференциальное уравнение распространения таких волн имеет вид:

^д p = c 2 Г±{A r - ^ p } 5 t ² rⁿ r    5 r

где 1 < n < 2.

Если n = 1, то имеем уравнение распространения цилиндрических волн, если n = 2 – уравнение распространения сферических волн.

Площадь псевдоцилиндрической поверхности определяется как:

S = 2 n r n .                    (4)

Транспортный поток (независимо от его плотности) можно рассматривать и как линейный источник шума (что значительно упрощает расчёты). Однако следует иметь в виду, что это допущение справедливо только для тех случаев, когда шумовой характеристикой потока, лежащей в основе расчета, является эквивалентный уровень звука за период времени, превышающий продолжительность прохождения транспортного средства. Квадрат звукового давления на расстоянии r от линейного источника записывается в виде:

p² = W p c/2 n r.          (5)

Уровень звукового давления (дБ) при его расположении на акустически жесткой поверхности Lp, определяется по формуле:

Lp= LW – 10 lg 2р r.         (6)

Для математического описания уличнодорожных транспортных сетей наиболее удобно использовать методы теории графов. Носителем информации о геометрии уличнодорожной сети города могут быть схемы автомобильных дорог, дорожные атласы, чертежи и др. Однако для построения шумовых карт необходимо преобразовать графическую информацию в аналитическую [4]. Граф представляет собой совокупность вершин и ребер. Информация о структуре графа представляется в виде матрицы.

Для математического описания уличнодорожных транспортных сетей методом теории графов и преобразования графической информации в аналитическую было осуществлено следующее.

Проанализирован математический аппарат описания и разработана математическая модель улично-дорожных транспортных сетей.

Наиболее удовлетворяющими описанию улично-дорожных сетей города являются модели, представляющие моделируемые категории (объекты, процессы, свойства) в виде множества графических символов (узлов, вершин) и отношений – предполагаемых или реальных связей между ними. Самое широкое распространение в настоящее время получили диаграммы в форме потоковых графов (графов состояний и переходов), деревьев событий (целей, свойств) и функциональных сетей различного предназначения и структуры, в том числе стохастической.

Как показывает опыт применения таких диаграмм, их основными достоинствами являются: высокая информативность представления и описания исследуемых категорий, хорошая наглядность и декомпозируе-мость, доступность и однозначность понимания исследователем и пользователем, удобство интерпретации и обработки на средствах вычислительной техники, возможность применения формализованных процедур анализа и синтеза таких моделей. Они позволяют описывать, а затем и оценивать предикаты первого, второго и высших порядков, являющихся соответственно их свойствами, отношениями между ними и другими категориями. Это достоинство обусловлено возможностью использования различных языков описания, позволяющих переходить от семантических (смысловых) моделей к семиотическим (знаковым) и использовать известные аппараты их исследования.

Из анализа структуры диаграммы влияния следует, что основными ее компонентами служат узлы (вершины) и связи (отношения) между ними. В качестве узлов обычно подразумеваются простейшие элементы моделируемых категорий (переменные или константы) – события, состояния, свойства, а в качестве связей – активности, работы, ресурсы и другие взаимодействия. Отношения или связи между переменными или константами в узлах диаграммы графически представляются в виде линий, называемых дугами или ребрами.

Каждые два соединенных между собой узла образуют ветвь диаграммы. В тех случаях, когда узлы связаны направленными дугами таким образом, что каждый из них является общим ровно для двух ветвей, возникают циклы или петли. Петли могут характеризоваться порядком, величина которого n определяется количеством не связанных между собой петель первого порядка. В свою очередь, петля первого порядка не должна содержать внутри себя других петель и обеспечивать достижимость ее любых узлов.

Переменные в узлах характеризуются фреймами данных - множеством выходов (значений, принимаемых переменными, неизменных во времени и между собой не пересекающихся) и условными распределениями вероятностей появления каждого из них. Условные распределения приписываются на диаграмме дугам или ребрам, соединяющим отдельные узлы. В вырожденных случаях вероятностного распределения узел может превращаться в константу, принимающую маргинальное (граничное) значение переменной. Вместо условных распределений допускается использование в диаграммах и отдельных значений, принимаемых переменными.

Однако для осуществления перехода от графических к математическим моделям необходима дополнительная символика.

Переменные и константы, подразумеваемые узлами диаграммы, в последующем будут обозначаться набором символов, объединенных в пять или четыре множества – в зависимости от их набора:

U = {1, 2, 3, ..., j, ... u} – множество узлов или вершин диаграммы;

V = {v1, v2, vj,   vu} – множество переменных, им соответствующих;

Ω _j = { ω ₁, ω ₂, ω ₃, ...} – набор значений, принимаемых j-ой переменной;

f_j ∈ F – плотность вероятности распределения переменной у;

π ∈ π– функция принадлежности линг- вистической переменной.

Для обозначения отношений между переменными (узлами, вершинами) диаграммы влияния, также будут использоваться соответствующие массивы символов. Эти массивы представлены следующими образом:

Dij = {d1, d2, d3, …} - множество дуг (ребер), соединяющих узлы i и j;

Aj - вектор дуг-предецессоров (выходящих из узлов, предшествующих данному узлу у и входящих в него);

Bj - вектор дуг-саксессеров (выходящих из рассматриваемого узла у и связывающих его с последующими узлами диаграммы);

Рij - вектор мер возможности или вероятности переходов между i и j;

Тij - вектор затрат ресурса (времени) при переходе из узла i в узел j.

Введенные обозначения позволяют легко формализовать и однозначно интерпретировать в последующем конкретный процесс или объект, представленный диаграммой влияния. Так, например, основные характеристики ее узлов (вершин) могут быть выражены таким кортежем:

Q , F, n >                (6)

а заданные диаграммой отношения или связи между ними – .

В свою очередь, математическое представление всей диаграммы влияния в общем случае может быть выражено следующей металингвистической формулой:

<Диаграмма влияния> :: =

= a V aQa F I -a D a A a B a P | Т> (7)

Геометрия двухстороннего графа G определяется матрицей инциденций (задающей номера вершин) и соответствующей матрицей координат {y(i)}. Каждому ребру {x(i1) , x(i2)} графа G сопоставляются числовые характеристики, описывающие улично-дорожную сеть:

• n - число полос;

• a - профиль дороги;

• в - качество покрытия;

• Y - директивы по структуре и динамике транспортного потока;

• 5    - метеорологические условия;

• 8    - окружающий ландшафт;

О - другие характеристики (освещённость, наличие распределительных полос, влияющих на диапазон скорости и др.).

Информация о структуре графа представляется в виде матрицы.

С использованием разработанной математической модели построены примерные улично-дорожные транспортные сети г. Тольятти. Транспортные сети состоят из дорог с интенсивной нагрузкой (выделяются в программе чёрной жирной полосой) и паутины местных дорог, дворовых подъездов. Введена нумерация узлов-вершин графа. Предусмотрена процедура очистки графа от несущественных деталей.

Разработаны также алгоритмы кодирования и восстановления информации о структуре графа улично-дорожной транспортной сети.

Можно с уверенностью утверждать, что какими-то одними методами (техническими, организации дорожного движения и др.) не удается обеспечить нормируемые значения транспортного шума. В этом случае оказываются весьма эффективными методы прогнозирования и оценки шума. Для данных целей наибольшее распространение получил метод составления карт уровней транспортного шума [1-4, 6, 7, 10-14]. При этом рассматривается именно транспортный шум и не включается шум от предприятий, внутриквартальных источников и т. п. Помимо прогнозирования транспортного шума, шумовые карты позволяют более эффективно разработать и внедрить мероприятия по снижению шума.

Карта шума характеризует состояние шумового климата в населенном пункте (городе) в период ее составления и на перспективу от всех видов транспортных средств в городе (населенном пункте). Она констатирует уровень шума на транспортных магистралях, определяет наиболее шумоопасные участки, позволяет рассчитать ожидаемые уровни шума на примагистральной территории и внутри зданий, расположенных на этой территории, а также для определения необходимых мероприятий по снижению шума.

Большим достоинством шумовых карт является их наглядность при оценке величин шума в любой из заданных точек селитебной зоны, возможность цветового и другого представления шумоопасных зон.

Традиционная карта транспортного шума представляет собой нанесенные на картографическом материале города или населенного пункта ожидаемые перспективные эквивалентные уровни звука на основных магистралях для больших городов в дневное и ночное время, для мелких городов — для дневного времени с указанием в характерных точках их номеров и уровней.

Способ обозначения эквивалентных уровней транспортного шума на участках магистралей может быть различным. Наиболее наглядным является варьирование интенсивностью цвета от светлого для низких уровней до более темного – для высоких. При этом ширина цветовой полосы соответствует количеству децибел А на данном участке в выбранном заранее масштабе.

Стремительное развитие вычислительной техники позволило автоматизировать процесс составления шумовых карт. Современные компьютеры с высокой скоростью обрабатывают огромные объемы информации как статистической так и графической. Одними из самых распространенных программных пакетов являются “LIMA”, “SoundPLAN” и др. [9-11, 14]. Эти пакеты интегрировали в себе методы построения графической (карт) информации, обработки баз данных параметров системы и методы визуализации для наглядного представления результатов работы.

В то же время анализ существующих карт транспортного шума показывает, что они отражают лишь текущее положение, существующую в данный момент (а то и в прошедшие периоды) шумовую картину. Она в основном лишь констатирует уровень шума в заданных точках селитебной территории и определяет наиболее шумоопасные участки. А ведь потенциальные возможности использования метода составления шумовых карт гораздо более широкие. Например, анализ шумовой карты может позволить рассчитать ожидаемые уровни шума на примагистраль- ной территории и внутри зданий, расположенных на этой территории, а также определить целесообразность мероприятий по снижению шума.

Авторами разработано программное обеспечение “Sound City Test”, позволяющее осуществлять расчет и сохранение в базе данных результатов измерения городского шума. Отличительной особенностью программы является возможность добавлять в базу данных карты районов и участков города и отображать на них результаты расчетов. В режиме отображения на карте программа выводит на экран график показывающий изменение шумовой обстановки в данной точке с течением времени. Это позволит строить прогноз улучшения или ухудшения шумовой обстановки.

При запуске программы открывается главное окно, в верхней части которого расположено меню, состоящее из двух пунктов – “Окна” и “Помощь”. Пункт меню “Окна” включает в себя следующие подпункты: “Ввод измерений”; “Карта” (рис. 3).

Выбор подпункта меню “Ввод измерений” приведет к открытию окна “Контрольные точки” (рис. 3). Окно логически разделено на две части – вверху “Ввод и редактирование точек”, внизу “Ввод и редактирование измерений в точках”.

Все точки представлены в специальной форме с сеткой. На экране представлена следующая информация:

• -    “Код точки”. Присваивается пользователем в соответствии с принятой системой кодировки точек;

• -    “Улица”. Выбирается из справочника улиц;

• -    “Комментарий”;

• -    “Карта”. Отображает название карты, на которой указана точка.

Для выбора нужной точки необходимо мышью указать на точку и нажать кнопку мыши. При этом черный треугольник справа переместится на указанную точку. После выбора нужной точки в нижней части окна отображается информация по измерениям привязанным к указанной точке.

Сразу под формой с сеткой расположены кнопки необходимые для работы с точками.

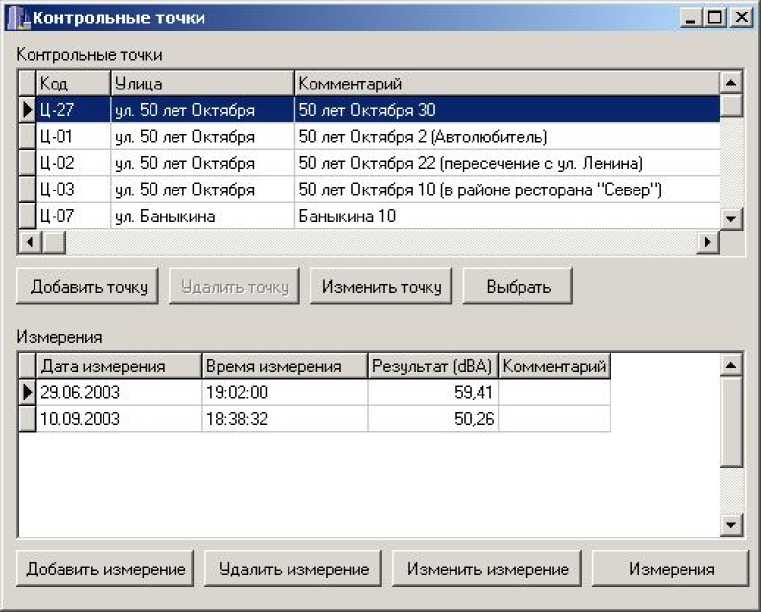
Рис. 3. Окно “Контрольные точки”

Кнопка “Добавить точку” позволяет добавить новую точку в базу данных. При нажатии на кнопку открывается новое окно, содержащее следующие поля для ввода информации:

• -    “Улица”;

• -    “Код точки”;

• -    “Комментарий”.

Окно содержит следующие поля для ввода информации:

• -    “Дата измерения”;

• -    “Время измерения”;

• -    “Комментарий”.

После заполнения полей необходимо нажать на кнопку “ОК”. При этом произойдет запись информации в базу данных. При нажатии на кнопку “Cancel” запись не произойдет.

Кнопка “Измерения” предназначена для ввода результатов измерений по существующей методике ГОСТ (рис. 4).

Авторами предложена методика моделирования транспортного шума и составления шумовых карт нового типа, позволяющих с достаточной степенью точности осуществлять прогнозирование изменения шумовой картины в той или иной шумоопасной зоне.

Согласно предложенному авторами методу, карты разрабатываются следующим образом: в определенных точках, расположенных в некоторой шумоопасной зоне (зонах), накапливаются результаты всех предыдущих измерений уровней шума и выдается заключение о динамике изменения уровня шума и ближайшей и долгосрочной перспективе. При этом метод представления результатов может быть различным – видеодецибелы, табличное представление, графики и др. (возможно и спектральное представление результатов измерений). Для карт данного типа авторами предложено название: динамические карты шума.

Составление динамических карт уровней шума в селитебной территории особенно эффективно для последующего прогнозирования и оценки шума селитебной территории, а также выбора тех или иных мероприятий по снижению шума в данной шумоопасной зоне. В настоящее время авторы реализуют идею динамических карт шума для анализа шумоопасных зон г. Тольятти. Так, в программном обеспечении “Sound City Test” имеется подпункт меню “Карта”, выбор которого приведет к открытию окна “Карта”.

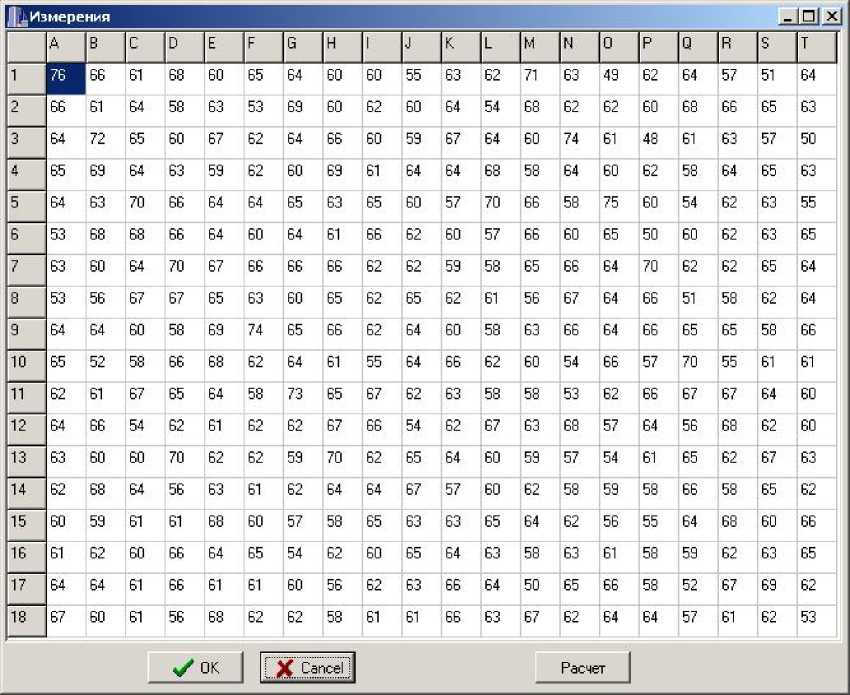
Рис. 4. Окно “Измерения”

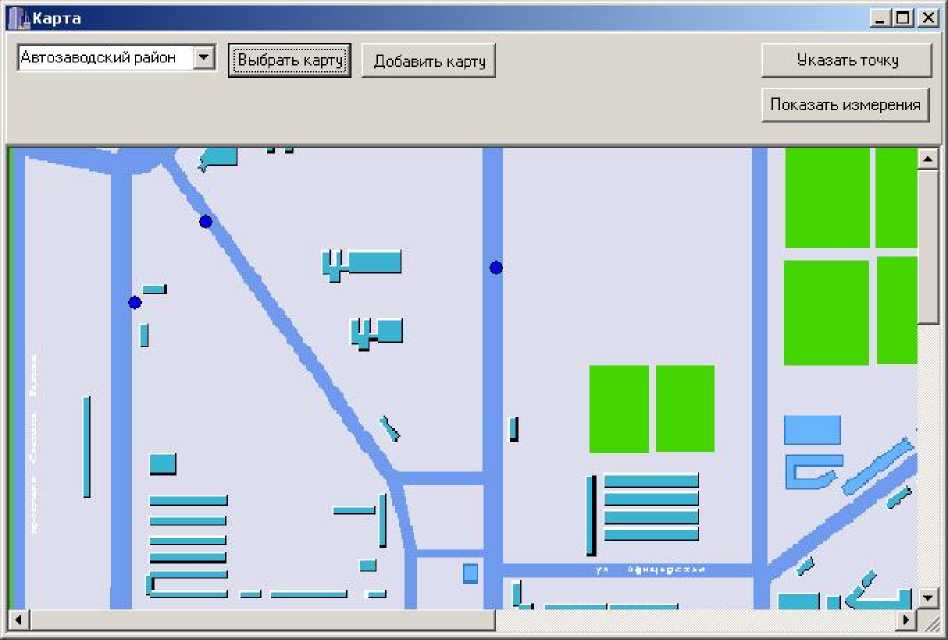
Рис. 5. Загрузка карты выбранного участка селитебной территории в окно

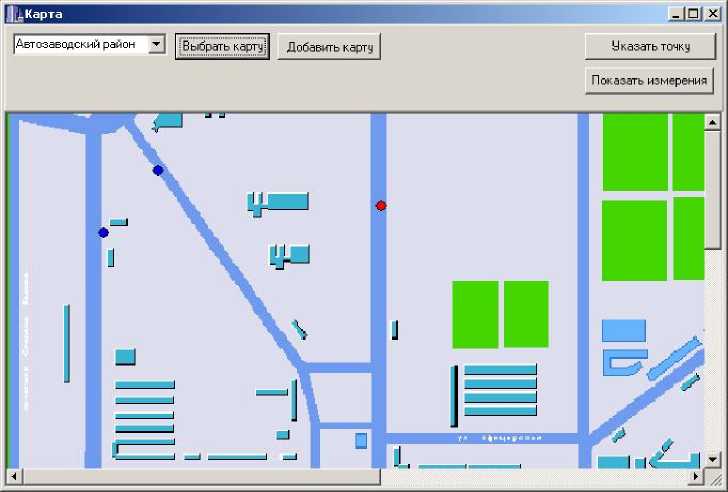
Рис. 6. Указание точки на карте

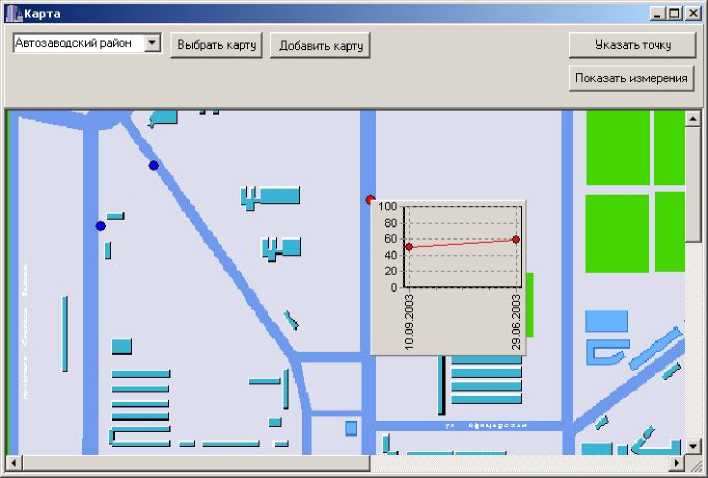
Рис. 7. Отображение измерений в виде графика

Вверху окна расположена панель управления с кнопками необходимыми для работы с картой. Для начала работы необходимо выбрать карту. Для этого в выпадающем списке выберите нужное название карты и нажмите кнопку “Выбрать”. При этом указанная карта загрузится в окно (рис. 5).

Как видно из рис. 5, одновременно с картой отобразились и некоторые контрольные точки. Для этих точек пользователем была заданна эта карат и указаны координаты расположения. При выборе другой карты все точки предыдущей карты с экрана будут удалены и загружены новые.

Для работы с точкой необходимо ее указать (рис. 6). После того как точка выбрана, у нее может быть изменено расположение или отображены введенные измерения в виде графика (рис. 7).

С использованием программного обеспечения авторами построены динамические шумовые карты селитебных зон Центрального, Комсомольского и Автозаводского районов г. Тольятти.