Моделирование распределения интенсивности в прозрачной среде с френелевскими границами, содержащей наночастицы алюминия

Методы спектроскопии светорассеивающих систем имеют широкую область приложений для мониторинга природных и технических объектов, способных как рассеивать, так и поглощать свет. Данные проблемы возникают при зондировании атмосферы [1], анализе биологических [2] и пищевых препаратов [3], изучении и оптимизации солнечных батарей [4], оптических детонаторов [5–10] и др. При анализе результатов экспериментальных исследований наиболее часто используются диффузионное приближение [11, 12], теория Кубелка–Мунка [11, 13] и решение уравнения переноса излучения методом Монте–Карло [14]. Причина их распространённости заключается в относительной простоте (диффузионное приближение и теория Кубелка– Мунка) либо в доступности готовых кодов для моделирования (метод Монте–Карло). Вместе с тем диффузионное приближение и теория Кубелка–Мунка применимы лишь в предельном случае очень сильного рассеяния света [11], и для них могут быть сформулированы только приближённые граничные условия [11]. В результате их предсказания могут приводить к значительным ошибкам [11, 13].

В большинстве работ по теории переноса излучения используются граничные условия Маршака [15], которые применимы как приближённые условия при рассмотрении границы, на которой не происходит изменения показателя преломления (облако в атмосфере). Данный вид граничных условий неприменим в случае систем, на границе которых происходит изменение показателя преломления: коллоидные растворы, наночастицы металлов, распределённые в прозрачной матрице, ячейки солнечных батарей и т. д. В этом случае необходимо рассмотрение граничных условий френелевского типа [16–19]. Решение уравнения переноса излучения с френелевскими граничными условиями методом дискретных ординат было осуществлено в [17]. В работе [18] было проведено моделирование переноса излучения в концентраторе солнечной энергии в случае сферических и стержневых люминесцирующих квантовых точек. В нашей работе [19] была предложена адаптация метода сферических гармоник к решению уравнения переноса излучения в однородном слое с вычислением интегральных коэффициентов поглощения, отражения и пропускания. В качестве объекта использовались прессованные поликристаллические образцы пентаэритриттетранитрата (тэна) с добавками наноразмер-ного алюминия. Сравнение теории и эксперимента позволило оценить комплексный показатель преломления наночастиц при длине волны лазерного излучения 643 нм [19].

Таким образом, применение теории переноса излучения к конкретным объектам является актуальным для развития спектроскопических методов их исследования. В большинстве работ рассматриваются интегральные характеристики, такие как коэффициенты диффузионного отражения и пропускания. Их использование не позволяет определить все неизвестные параметры рассеивающей среды, становится необходимым использовать дополнительную информацию о системе, что снижает возможности метода. Для повышения информативности может быть использовано угловое распределение отражённого и прошедшего света, которое не было рассмотрено в нашей предыдущей работе [19].

Цель работы: моделирование углового распределения интенсивности прошедшего и отражённого света от прозрачной среды, содержащей наночастицы металла. В качестве модельной системы использованы образцы тэна, содержащие наночастицы алюминия различного радиуса. Выбор данной системы обусловлен возможностью её применения в качестве капсюльных составов для оптических детонаторов [5–10], а также тем, что вещество матрицы (тэн) может быть спрессовано с получением плотного и оптически прозрачного образца без видимых дефектов. Расчёты выполнены при значении длины волны 1064 нм (первая гармоника неодимового лазера), что соответствует условиям инициирования капсульных составов для оптических детонаторов в экспериментальных работах [8–10].

Метод сферических гармоник при френелевских границах

Рассмотрим слой прозрачного вещества, в котором однородно распределены металлические частицы с достаточно малой концентрацией, так, что их взаимодействием можно пренебречь. Стационарное распространение неполяризованного света в такой системе описывается уравнением переноса излучения, которое имеет вид [11]:

( 1- v ) I ( r ,l ) = - kl ( r , 1 ) +

+ к Л f I ( r -^!> ( l ^{- 1} ' ) d l '⁺ q ( r ,¹ ) •

где I ( r , ^ˆ l ) – интенсивность света в точке r в направлении ^ˆ l , k – линейный показатель экстинкции, Л = k sca / к - альбедо однократного взаимодействия кванта света с рассеивающей средой, x ( 1 ,1 ' ) - индикатриса рассеяния, q ( r ,^ˆ l ) – функция источников света. Член в левой части уравнения имеет смысл изменения интенсивности в направлении ^ˆ l при изменении пространственной координаты. В правой части первое слагаемое указывает причину уменьшения интенсивности – экстинкцию света, второе – увеличения её из-за рассеивания, третье слагаемое – увеличение интенсивности за счёт источников света, находящихся внутри рассеивающей свет среды. Будем полагать, что уширение пучка за счёт процессов рассеяния значительно меньше радиуса пучка, падающего перпендикулярно на верхнюю поверхность образца, что позволяет перейти к одномерной задаче. С учётом данных упрощений уравнение переноса излучения принимает вид [15, 19]:

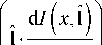
d x

V          7

= ^{— kl} ( x ^-1 ) + 2 f I ( x ,' ' ) ■ * ( l ^{- 1} ' ) ^d1 '

Переходя к безразмерной координате т = kx и вводя косинус сферического угла ц = cos 9 между направлением начального падения луча перпендикулярно верхней границе образца и интересующим направлением, приведём (2) к виду [15, 19]:

Ц d I ⁽ d x ’ ^{Ц )} =— I ( x , ц ) + у j I ( x - Ц' ) ■ x ( ц - Ц' ) d ц' . (3) — 1

Для решения уравнения (3) был использован метод сферических гармоник, в рамках которого угловое распределение интенсивности света ищется в виде суперпозиции сферических гармоник [15, 19]. Поскольку мы пренебрегаем уширением пучка света и зависимость от полярного угла φ отсутствует, сферические гармоники могут быть заменены полиномами Лежандра ( P l ):

I ( x - 1 ) = Е + 1 C l ( x ) ■ P. М»

I = 0    ²

» f ; ' C i ( x ) ■ p ( ц ) , l = 0 2

где N – максимальный учитываемый порядок гармоник, С l – зависящие от координаты коэффициенты разложения. Индикатриса рассеяния может быть разложена по полиномам Лежандра [15, 19]:

^x ( ^{1 -1} ' ) = E 2l + 1 x - P ( ц , ц' ) » = 0 2

V 2 l + ¹

» L™ ^xi ■ P ( ц , ц ) .

l = 0 2

После преобразования второго слагаемого уравнения (1) и применения рекуррентных соотношений для полиномов Лежандра система уравнений для коэффициентов разложения интенсивности по ним принимает вид [15, 19]:

2 m + 1

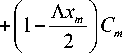
dCm dT

dCm dT

Формула (6) известна как система уравнений сферических гармоник. Непосредственное применение системы уравнений (6) затруднительно, так как при учёте граничного условия, выражающего падение излучения извне на образец, угловое распределение будет сильно вытянуто в направлении исходного пучка. Для устранения этого недостатка было предложено вычитать из решения часть, связанную с непосредственно падающим светом I 0 [15, 19], и вычислять только рассеянную составляющую I s :

I = 1 0 + I s . (7)

Нерассеянная составляющая интенсивности ( I 0 ) уменьшается в соответствии с законом Бугера. Поскольку в некоторых случаях будут рассматриваться достаточно тонкие образцы, в ней должно быть учтено отражение от задней границы образца. Поэтому нерассеянная компонента решения принимает вид:

1 ₀ = J ■ ( exp ( —т ) + R f exp ( т — 2 L ) ) , (8)

где J – плотность мощности излучения, прошедшая внутрь образца, R f – коэффициент френелевского отражения от поверхности при нормальном падении луча. Система уравнений для рассеянной составляющей имеет вид:

2 m + 1

d C 1 d C

+

+ 1-- m C

I 2 7

d T         d T _

J "2 x¹ [ exp ( —t ) + R f exp ( t — 2 L ) ] .

Сформулируем граничные условия для системы (9). Будем полагать, что частицы не находятся непо-

средственно на поверхности образца. Тогда взаимодействие света с поверхностью будет описываться формулами Френеля [16– 19]:

Два последних слагаемых являются частным ре-

шением

I s ( 0, ц ) = R ( ц ) I s ( 0, -ц ) , 0 <ц< 1,

I s ( L , -ц ) = R ( ц ) I s ( 0, ц ) , - 1 <ц< 0,

C ¹ _p и C_p ² равны:

неоднородного уравнения. Коэффициенты

где R ( ц ) - угловая зависимость френелевского коэффициента отражения. Формулы (10) дают условия на передней и задней границах образца соответственно. Их необходимо преобразовать в соотношения для вкладов гармоник на поверхности. Для этого исполь-

где

p

p

N

=- J ^A' Z [^g p-

m = 0

""I-1

^{+ A}pm J   ^Bm ,

N

= J A R f exp ( - 2 L ) - К [б pm m = 0

""I-1

- ^Apm J   ^Bm ,

зуем разложение интенсивности на поверхности по полиномам Лежандра:

К 2m+1 Cm (0) Pm (ц) = m=0 2

= К      (-1) X ( 0)-Pm (ц)-R (ц) .

m = 0 2

Умножив уравнение на P l ( ц ) и проинтегрировав от 0 до 1 (углы, попадающие внутрь среды), получим для передней и задней границ соответственно:

N

К N m - R m ) C m ( 0 ) = 0, m = 0

N

К ( ^Vlm - R Im ) C m ( L ) = 0, m = 0

где матричные элементы имеют вид:

R lm = ( - 1 ) m       J P m ( ц ) R ( ц ) P l ( ц ) d Ц ,

N m = 2 ^ + 1 J P m ( ц ) P ( ц ) d ц ,                (13)

N m = ( - 1 )X ,

R m = ( - 1 ) m R Im .

В соответствии с формулами Френеля угловая за висимость коэффициента отражения при ц > V1 - n-2

определяется выражением:

R ( ц ) = 1 ^f V n - ² - ^{1 +ц} 2

ц

n

,-2

1 + ц ² + ц

X

Л

X

ц ² + 1

Так как свет считается неполяризованным, выражение (14) содержит вклады s- и р-поляризации, которым отвечают первое и второе слагаемые в квадратных скобках соответственно. При ц <  V1 - n ^{- 2}

происходит полное внутреннее отражение и R ( ц ) = 1.

Решение (9) можно представить в виде:

^Cm ( ^Т ) = К a ml^CI exP ( Y I ^T ) ⁺

I = 0

+ C p exp ( -T ) + C p exp ( t ) .

A pm

и B

J p i¹ g 2 p +1

2 p + 1

P , P '- I

-1

fl ^{Л Х} m |X

I ¹ Y j⁸ p ' m

m + 1 g 2 m + 1 ¹

m

------5

2 m + 1

m , m '- 1

1 [ xmL

.

Степень «–1» означает взятие обратной матрицы от матрицы, элементы которой приведены в квадратных скобках. Между множителями в квадратных скобках делается операция матричного умножения.

Первое слагаемое в правой части (15) соответствует разложению решения по собственным векторам матрицы A_pm (матрица a_ml ) с соответствующими собственными числами y l . Коэффициенты разложения C l должны определяться из граничных условий (10). Данные граничные условия образуют систему из 2 N +2 уравнений, из которых 2 N линейно независимы. Число определяемых коэффициентов равно N + 1, то есть система переопределённая. Поэтому использовалась минимизация суммы квадратов отклонений величин в левых частях (10) от нуля. В результате получим для коэффициентов следующее уравнение, записанное в матричной форме:

C: = -[ ( Za ) ^T ( Za | ( Za ) T ( ZC p ) , (17)

где Z =

f N - R 'P ( N - R 'J

f a । a = I                I, CP =

I a - exp ( -у L )l     ^p

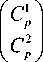
Альтернативный способ определения коэффициентов C_l заключается в применении сингулярного разложения матрицы Z [20]. Данный метод также обеспечивает удовлетворительное приближение, но подразумевает произвол при исключении малых собственных чисел матрицы, который может влиять на точность результата.

Параметры рассеивающей среды вычислялись при помощи теории Ми [5 –7, 9, 21, 22], считая наночастицы алюминия сферическими. Данная теория позволяет рассчитывать как сечения поглощения и рассеяния, так и индикатрису рассеяния. Комплексный показатель преломления металла для длины волны 1064 нм (первая гармоника неодимового лазера) составлял 0,96–8,07 i [23], показатель преломления матрицы был равен 1,54. Количество гармоник, используемое при расчёте, определялось исходя из анизотропии индикатрисы рассеяния. Чем больше анизотропия индикатрисы, тем большее количество гармо-

ник необходимо использовать для её корректного описания и получения достоверных результатов. Максимальный радиус наночастиц алюминия в расчёте составлял 700 нм, что приводит к сильно анизотропной индикатрисе рассеяния, для аппроксимации которой было использовано N = 31. При меньшем количестве гармоник угловая составляющая приобретала осциллирующую структуру, которая исчезала при увеличении числа гармоник. Аналогичные особенности расчёта отмечались и другими авторами [24].

Компьютерная реализация

Для компьютерной реализации решения уравнения переноса излучения методом сферических гармоник в слое с френелевскими границами был написан специальный программный комплекс. Согласно постановке задачи, расчёты проводились для прозрачной среды, содержащей наночастицы металлов. В качестве входных параметров программы использовались радиус наночастиц металла, длина волны света, комплексный показатель преломления металла и показатель преломления прозрачной среды на этой длине волны, толщина слоя вещества, плотности металла и прозрачной среды и массовая доля наночастиц металла.

Программный комплекс включал следующие основные блоки:

• 1.    Расчёт коэффициентов эффективности поглощения и рассеяния, а также индикатрисы рассеяния в рамках теории Ми для задаваемого радиуса и материала наночастицы.

• 2.    Расчёт линейных показателей поглощения и рассеяния среды при заданной природе, массовой доле и радиусе наночастиц металла. Определение альбедо однократного рассеяния. Аппроксимация индикатрисы рассеяния в виде ряда по полиномам Лежандра.

• 3.    Вычисление матриц коэффициентов в системе уравнений сферических гармоник (9), матриц граничных условий (14), матриц коэффициентов в уравнениях (15)–(16), описывающих уравнение переноса излучения, разрешённое относительно производных, и частное решение неоднородного уравнения.

• 4.    Решение матричных уравнений (12) при помощи формулы (17), определение коэффициентов разложения решения однородного уравнения по собственным векторам из френелевских граничных условий задачи.

• 5.    Вычисление углового распределения интенсивности излучения в задаваемых точках, построение графиков рассчитанных зависимостей, расчёт пропускания и отражения слоя.

Для апробации работы программы был выполнен тестовый расчёт распределения поглощённой энергии излучения при Qsca = 1,0; Qabs = 0,01. В данной области параметров должен наблюдаться диффузионный режим рассеяния света [11], в котором наблюдаемый безразмерный показатель поглощения должен быть близок к ^3 -(1 -Л) . Полученная в расчёте величина наблюдаемого безразмерного показателя поглощения составляет 0,1775 и отличается на 3% от предсказываемого теоретически значения, что свидетельствует о корректности расчёта.

Результаты и обсуждение

На рис. 1 и 2 представлены результаты моделирования угловой зависимости отражённого и пропущенного излучения для образцов, содержащих наночастицы алюминия различного радиуса с массовой долей 0,05%. В качестве направления, от которого отсчитывается угол, выбрано направление падения излучения перпендикулярно передней поверхности образца. Толщина слоя образца задавалась равной длине экстинкции, умноженной на 4, для получения сопоставимых результатов. Рассмотрим основные особенности полученных угловых зависимостей. В случае отражённого света распределение интенсивности имеет пологий минимум в области θ < 0,2π (направление внутрь образца перпендикулярно передней поверхности), далее возрастание практически до стационарного значения. Для больших радиусов частиц далее наблюдается возрастание с появлением максимума при θ = π.

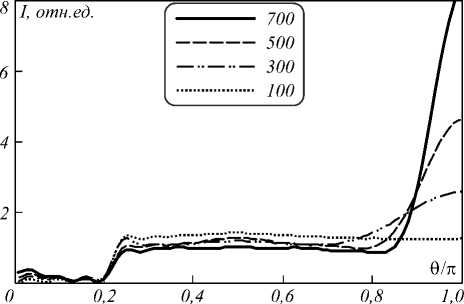
Рис. 1. Угловое распределение интенсивности в отражённом свете

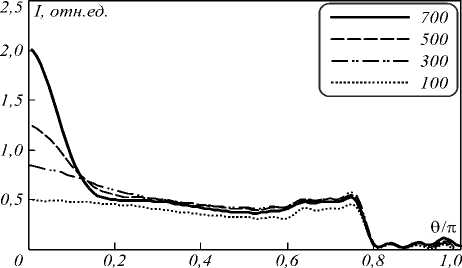
Рис. 2. Угловое распределение интенсивности в прошедшем свете

Отмеченные особенности связаны с двумя причинами: френелевской зависимостью коэффициента отражения света от угла падения и фактором анизотропии рассеяния. Френелевская зависимость коэффициента отражения при использованном коэффициенте преломления среды представлена на рис. 3. В области углов падения

0,23π≥θ≥π коэффициент отражения равен единице: происходит полное внутреннее отражение. Пропускание границы резко увеличивается, а коэффициент отражения уменьшается в 6,7 раза при изменении угла падения от 0,225 π до 0,2 π. После этого он уменьшается ещё, становясь минимальным при θ =0 и равным (n – 1)2/(n + 1)2 = 0,045. Сравнивая рис. 1 и рис. 3, убеждаем- ся, что увеличение интенсивности отражённого света происходит в той же области углов падения, что и воз-

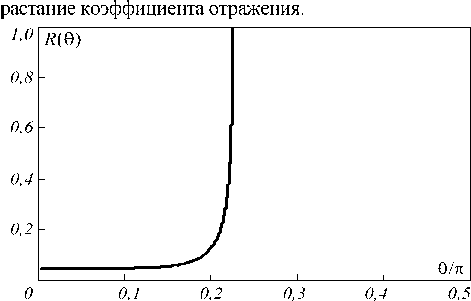
Рис. 3. Зависимость коэффициента отражения от угла падения

Сопоставим данную особенность углового распределения с полученными другими авторами. В качестве примера рассмотрим работу [12], в которой было вычислено угловое распределение рассеянного излучения в диффузионном приближении при различных углах падения света на бесконечный плоскопараллельный слой рассеивающей, но не поглощающей среды. Показано [12], что в случае нормального падения света угловое распределение на поверхности симметрично. Чем выше угол падения (относительно нормали к поверхности), тем распределение более асимметрично, причём степень асимметричности уменьшается с ростом толщины рассеивающего слоя. Причина заключается в том, что при малой толщине слоя преобладает однократное рассеяние, а при больших толщинах – многократное, со «стиранием памяти» об изначальном направлении. В наших расчётах был исследован только случай нормального падения излучения на рассеивающую среду и, в отличие от работы [12], было обнаружено несимметричное угловое распределение. Несимметричность углового распределения интенсивности связана с угловой зависимостью френелевского коэффициента отражения, которая не рассматривалась в работе [12]. Следует также отметить, что диффузионное приближение не может быть использовано для решения уравнения переноса излучения в области с френелевскими граничными условиями. Диффузионное приближение эквивалентно использованию только двух членов разложения интенсивности в ряд по полиномам Лежандра в (4). Данная аппроксимация не позволяет достаточно точно описать зависимость коэффициента отражения света от границы с помощью того же ряда. Поэтому в диффузионном приближении всегда применяются не- точные граничные условия, основанные на законе сохранения энергии и не учитывающие угловых зависимостей [11, 12].

Влияние фактора анизотропии проявляется в резком возрастании интенсивности отражённого света при θ ≈ π. По мере увеличения радиуса наночастицы фактор анизотропии, который равен косинусу среднего угла рассеяния g = 〈 cos θ〉 , уменьшается от –0,185 до –0,945. То есть чем больше радиус наночастицы, тем больше излучения отражается в обратном направлении. Эта особенность существует не только на угловых зависимостях интенсивности на границах, но и внутри образца. В качестве примера на рис. 4 представлено угловое распределение интенсивности в центре. Зависимости, рассчитанные для наночастиц большого радиуса, имеют два локальных максимума при θ ≈ ±π, связанные с доминирующим направлением рассеяния. В случае наночастиц малого радиуса (100 нм) данные локальные максимумы не наблюдаются, а зависимость интенсивности от угла очень слабая.

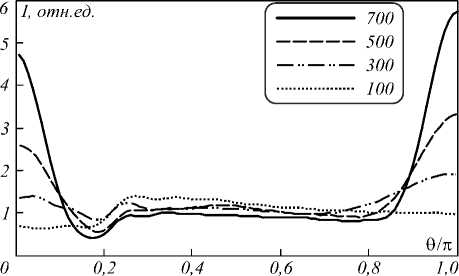
Рис. 4. Угловое распределение интенсивности в центе образца

В физике светорассеивающих систем часто используется понятие « ламбертовая поверхность » – поверхность, интенсивность отражения от которой во всех направлениях одинакова. Согласно рис. 1, интенсивность излучения практически не зависит от угла в области 0,24π≤θ≤π в случае наночастиц алюминия малого радиуса, что связано с малой анизотропией рассеяния света на них. Таким образом, если анизотропия рассеяния света мала, несмотря на граничные условия френелевского типа, отражение от широкого слоя рассеивающей среды будет близко к изотропному. Увеличение или уменьшение фактора анизотропии будет приводить ко всё большим отклонениям от приближения ламбертовой поверхности.

Рассмотрим информативность углового распределения излучения при решении обратной задачи. Ранее нами в [19] было проведено определение оптических свойств наночастиц алюминия в среде с френелевскими границами с использованием фотометрического шара. На основе экспериментальных коэффициентов отражения и пропускания, измеренных в зависимости от толщины образца и массовой доли наночастиц алюминия (средний радиус 50 нм), определялся комплексный показатель преломления алюминия. Как следует из результатов настоящей работы, основным параметром, влияющим на угловое распределение излучения на границе образца, является фактор анизотропии индикатрисы рассеяния. Поэтому экспериментальное определение угловой зависимости интенсивности разумно, если ожидается сильно анизотропное рассеяние.

Заключение

В работе рассмотрено решение уравнения переноса излучения в слое рассеивающей среды с френелевскими границами методом сферических гармоник. В качестве примера использовано распространение света в диэлектрической среде, содержащей наночастицы алюминия. Приведены основные блоки написанной компьютерной программы для моделирования переноса излучения. Рассчитаны угловые распределения интенсивности на границах и в центре слоя. Сделан вывод, что френелевские граничные условия приводят к несимметричному угловому распределению интенсивности на границах слоя. Показано, что в случае сильно анизотропной индикатрисы рассеяния распределение интенсивности на поверхностях образца вытянуто в сторону нормали, направленной от поверхности в окружающее пространство, что может быть использовано при решении обратных задач спектроскопии светорассеивающих систем.

Работа выполнена при финансовой поддержке РФФИ (грант № 14-03-00534 А) и Министерства образования и науки РФ (госзадание № 2014/64).