Моделирование распределения освещённости в плоскости регистратора космического гиперспектрометра, основанного на схеме Оффнера

На сегодняшний день в мире происходит рост рынка дистанционного зондирования Земли (ДЗЗ), развитие методов обработки и классификации информации. Это обусловлено в первую очередь ростом числа активных космических аппаратов (КА), а также видов информации ДЗЗ, получаемых с КА. Аппаратура ДЗЗ позволяет проводить периодическую съёмку земной поверхности и таким образом наблюдать за изменениями окружающей среды [1]. Гиперспектральное ДЗЗ является перспективным направлением развития рынка ДЗЗ. Оно позволяет решать множество тематических задач. Области и разделы тематических задач, решаемых с использованием гиперспектральных систем, представлены в [2].

Помимо развития методов обработки, на сегодня существует тенденция к уменьшению массогабаритных характеристик самой гиперспектральной аппаратуры. В данном отношении перспективной является конструкция аппаратуры, основанной на схеме Оффнера [3–6]. Концепция данного компактного гиперспектрометра для малого КА представлена в работах [7– 10].

Проектирование такой аппаратуры должно исходить:

– из класса решаемых тематических задач ДЗЗ [2],

– условий функционирования в космическом пространстве.

К космическим условиям функционирования относятся: высота, угол, время съёмки, энергетическая яркость подстилающей поверхности на момент съёмки и пр.

Одним из требований к рабочим характеристикам аппаратуры является отношение сигнал/шум на фо-топриёмном устройстве в заданных условиях съёмки. При оценках данного отношения важно учитывать энергетические характеристики электромагнитного излучения, приходящего в единицу времени на единицу площади фокальной плоскости аппаратуры.

В работах [3 – 11] приведено описание различных конструкций гиперспектрометра на основе схемы Оффнера.

В работе [12] проведено экспериментальное исследование дифракционной решётки на поверхности выпуклого зеркала. Показано, что распределение энергии по порядкам дифракции согласуется с результатами моделирования.

В работе [13] также рассмотрен математический аппарат для расчёта распределения освещённости для спектрометра на основе схемы Оффнера в лабораторных условиях.

Актуальным является вопрос оценки уровня освещённости в плоскости регистратора гиперспектрометра для космических условий функционирования.

1.    Постановка задачи

Величина потока в плоскости изображения оптической телескопической системы, с одной стороны, определяется площадью и яркостью в предметной плоскости объектива, с другой – величиной его передней апертуры, экранированием и виньетированием элементами конструкции, диафрагмами, крепёжными устройствами и пр. Для расчёта освещённости в плоскости регистратора космического гиперспектрометра необходимо провести трассировку лучей в его оптической системе (ОС) с учётом аберраций и потока энергии, приходящего на входной зрачок.

Для расчёта освещённости была взята математическая модель гиперспектрометра, изображенного на рис. 1.

Параметры объектива:

– дифракционно ограниченный катадиоптрический телескоп,

– фокусное расстояние ~300 мм,

– диаметр главного зеркала (ГЗ) – 60 мм.

– диаметр вторичного зеркала (ВЗ) – 30 мм.

Параметры гиперспектрального блока на основе схемы Оффнера [11– 13]:

– радиус кривизны большого сферического зеркала (БЗ) – 159,6 мм,

– радиус кривизны зеркала с дифракционной решёткой (ЗсДР) – 80,6 мм, частота штрихов – 30 линий на 1 мм.

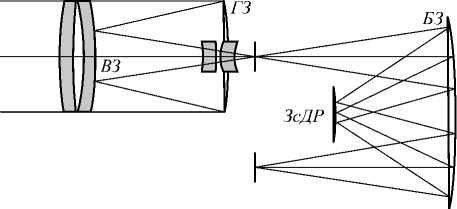
Рис. 1. Оптическая схема гиперспектрометра

На выходе расположен регистратор, представляющий фотоматрицу, которая преобразует оптический сигнал в электрический.

2.    Исходные данные

В качестве исходных данных в предметной плоскости для моделирования могут быть взяты табличные значения:

– E 1 ( λ , h S ) – спектральной облучённости подстилающей поверхности Земли в зависимости от высот Солнца над горизонтом (высота Солнца над горизонтом равна углу падения солнечных лучей на поверхность Земли),

– L 2 ( λ , h S , ψ ) – спектральной плотности энергетической яркости (СПЭЯ) атмосферы (дымки) Земли для различных высот Солнца над горизонтом и углов визирования,

– τ атм ( λ ) – интегрального по оптическому пути, спектрального коэффициента пропускания атмосферы.

Выражение для спектральной плотности энергетической яркости при условии, что поверхность Земли рассеивает излучение во всех направлениях полупространства равномерно, имеет вид:

L 1 ( λ , h S , ρ ) = ( E 1 ( λ , h S )/ π ) ρ ,

где L 1 – СПЭЯ участка поверхности, E 1 ( λ , h S ) – спектральная облучённость поверхности Земли, λ – длина волны, h s – высота Солнца над горизонтом, ρ – альбедо поверхности (альбедо называется коэффициент диффузного отражения).

Обозначим суммарную яркость в направлении ви- зирования объектива:

L ( λ , h S , ρ , ψ ) = L 1 ( λ , h S , ρ , ψ ) τ атм ( λ ) ^{(1/cos( ψ ))} + + L ₂( λ , h_S , ψ ),

где τ атм ( λ ) – интегральный коэффициент пропускания атмосферы в надир, ψ – угол визирования, L 2 ( λ , h S , ψ ) – СПЭЯ атмосферы (дымки) в направлении визирования.

• 3.    Моделирование освещённости в плоскости детектора в приближении геометрической оптики

Выполним оценку уровня освещённости в плоскости регистратора гиперспектрометра. Для расчёта бу- дем использовать метод трассировки лучей через оптическую систему, изображённую на рис. 1.

Разобьём предметную плоскость на элементарные площадки. Рассмотрим расчёт освещённости от элементарной площадки. Набор k лучей, исходящих из центра элементарной площадки S k с яркостью L в направлении визирования ψ , создают поток на входном зрачке ОС [15]:

∆Φ k ( λ , h S , ρ , ψ , Ω k ) = S k L ( λ , h S , ρ , ψ ) ∆Ω k .         (3)

∆Ω k – телесный угол конуса лучей с вершиной в центре элементарной площадки и с основанием на входном зрачке ОС:

∆Ω k = ( S ВЗ ⋅ cos( ε ))/ r ² ,                               (4)

где S ВЗ – площадь элемента входного зрачка ОС, ε – угол падения на входной зрачок, r – расстояние между S k и S ВЗ . При условии космической съёмки за величину r можно принять дальность съёмки.

Выражение для потока излучения прошедшего ОС объектива [15]:

∆Φ ¹ k ( λ , h S , ρ , ψ , Ω k ) = τ k ( λ ) ∆Φ k ( λ , h S , ρ , ψ , Ω k ), (5) где τ k ( λ ) – коэффициент пропускания оптической системы.

На основании результатов, приведённых в работах [13, 15], выражение для распределения освещённости, формируемое площадкой ∆ S k , расположенной в предметной плоскости (на Земле) в направлении визирования ψ , можно представить в виде:

2 π π

H mk ( x , y , λ ) = C m ( λ ) ∫ ∫∫ ∆Ω k τ k ( λ ) L ( λ , h S , ρ , ψ ) × ∆ S_k 0 0

×δ ( x - x ɶ _k ( u , v , θ , φ , λ ), y - y ɶ _k ( u , v , θ , φ , λ )) ×               (6)

× sin ² θ d θ d φ d u d v ,

H mk ( x , y , λ ) – освещённость в плоскости регистратора в точке с декартовыми координатами ( x , y ) для длины волны λ , δ ( x , y ) – регулярная аппроксимация сингулярной функции Дирака, x ɶ _k , y ɶ _k – координаты прихода луча в плоскость регистратора, исходящего из k -й площадки предметной плоскости в направлении, определяемом углами ( θ , φ ), C m ( λ ) – интенсивность порядка дифракции с номером m. Интегрирование ведётся по всем точкам с декартовыми координатами ( u , v ) площадки Δ S k предметной плоскости и по всем направлениям лучей, которые попадают в плоскость регистратора. В качестве регулярной аппроксимации сингулярной функции Дирака используется следующая гладкая функция

δ ( x , y ) = (1/2 πσ ² ) exp ( - ( x ² + y ² )/2 σ ² ) ,           (7)

где 6σ = Δ, Δ – размер пиксела фотоприемника. Функция Hmk(x, y, λ) с точностью до нормировки практически совпадает с функцией рассеяния точки (ФРТ) гиперспектрометра, так как размер площадки достаточно мал и его можно считать точечным источником. В отличие от ФРТ, Hmk(x, y, λ) измеряется в энергетиче- ских единицах. Её можно использовать для определ е-ния характеристик фотоматрицы регистратора. Полученную функцию в дальнейшем можно использовать для расчёта характеристик гиперспектрального изображения. Освещённость изображения в плоскости регистратора при съёмке произвольного участка Земли является сумм ой освещённостей элементарных участков ΔSk. Общая формула для расчёта освещённости в плоскости регистратора на основе ФРТ приведена в работе [13].

• 4.    Результаты расчёта освещённости

в плоскости регистратора гиперспектрометра от элементарной площадки на поверхности Земли

В расчётах под условиями космического функционирования были приняты: высота съёмки H = 600 км, угол визир ования ψ , высота Солнца над горизонтом h S , альбедо поверхности ρ.

Для расчёта была взята площадка подстилающей поверхности, центр которой расположен на оси визирования гиперспектральной аппаратуры. При расчётах площадка размером 30×30 м² разбивалась на 100 равных частей. Среднее альбедо поверхности ρ = 0,4. Распределение освещённости в плоскости изображения гиперспектрометра представлено на рис. 2, результаты расчёта средней освещённости засвеченной зоны от уровня не ниже 1/2 максимальной освещённости представлены в табл. 1.

Табл. 1. Расчётная средняя освещённость от уровня не ниже 1/2 максимальной освещённости в плоскости изображения при съёмке в надир (от площадки 30×30 м2), в относительных единицах E0, Вт/м2

Длина волны, нм	Высота солнца
	10	40	70
500	0,5248	1,9666	2,9905
600	0,4520	1,8149	2,7733
700	0,3980	1,5637	2,3616

Рис. 2. Распределение освещённости распределения (для длины волны 500 нм) в плоскости регистратора гиперспектрометра, основанного на схеме Оффнера, полученное от площадки размером 30×30 м2, с высоты 600 км

Значение осв ещённости для порядка дифракции можно оценить по формуле:

E = С m E o ,                                      (8)

где C m – интенсивность дифракционного порядка, E 0 – описывает освещённость, не распределённую по порядкам дифракции.

• 5.    Оценка адекватности результатов расчёта освещённости

Оценку освещённости в плоскости изображения объектива также можно провести с использованием известных параксиальных формул:

Φ = π⋅ L ⋅ S _ВЗ ⋅ sin ² ( u ),

E = ε⋅ τ⋅ Φ / S ФП ,                                  (9)

ε=1-(D2/D1)2, где Ф – световой поток на входном зрачке, E – освещённость в фокальной плоскости, L – яркость площадки Sk, SФП – площадь изображения, u – апертурный угол объектива, τ – пропускание ОС, ε – коэффициент центрального экранирования, D1 – диаметр главного зеркала, D2 – диаметр вторичного зеркала. Формулы приведены без учёта величины виньетирования светов ого потока объективом.

Пусть съёмка проводится в надире, альбедо – 0,4, высота солнца – 70 ° , длина волны λ =500 нм. Параметры атмосферы следующие:

– спектральная облучённость земной поверхности E 1 ( λ , h S )= 1810 Вт/м² ⋅ нм,

– СПЭЯ дымки L 2 ( λ , h S , ψ ) =45,5 Вт/м² ⋅ нм ⋅ ср,

– интегральный по оптическому пути спектральный коэффициент пропускания атмосферы τ атм = 0,69.

Параметры оптической системы указаны в п. 1 данной статьи, где интегральный коэффициент пропускания оптики τ = 0,8.

Если принять в расчёт площадку земной поверхности размерами 30×30 м², снимаемую с высоты H = 600 км, то несложно получить, что:

S _ФП = 15 × 15 мкм ² , Φ= 1,1565 ⋅ 10 ^{- 9} Вт,

E = 3,8550 Вт/м2, где SФП – площадь изображения, Ф – поток, падающий на фокальную плоскость, E – средняя осв ещён-ность в фокальной плоскости объектива.

Расчётное значение потока на входном зрачке и средней освещённости (от уровня не ниже 1/2 максимальной осв ещённости) в плоскости изображения гиперспектрометра при тех же модельных параметрах ОС и атмосферы:

Φ= 1,0326 ⋅ 10 ^{- 9} Вт, E = C_m ⋅ 2,9905Вт/м ² .

Полученные значения можно использовать для подбора характеристик фотоматрицы регистратора.

Заключение

В работе рассмотрены основные соотношения для моделирования освещённости, численные методы расчёта освещённости, проведен расчёт освещённости для гиперспектрометра, состоящего из объектива и спек- трометра на основе схемы Оффнера, с использованием табличных значений параметров спектральной облучённости подстилающей поверхности Земли, спектральной плотности яркости дымки Земли, спектрального коэффициента пропускания атмосферы в зависимости от высот Солнца над горизонтом и угла визирования. Результаты расчетов можно использовать для выбора параметров фотоматрицы регистратора.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант 16-29-09528 офи_м).