Моделирование распределения температуры в ходе производства металлокерамических труб методом центробежного СВС

Совершенствование технологии получения композиционных слоистых металлокерамических труб с внешним металлическим и внутренним керамическим слоями с помощью реакций саморас-пространяющегося высокотемпературного синтеза (СВС), разработанной в 70-х годах прошлого века, до настоящего времени остаётся актуальной задачей. Стальные трубы, покрытые внутренним керамическим слоем, могут использоваться для транспортировки абразивных материалов в угольной и металлургической промышленности, теплоэнергетике и т. п., поскольку обладают устойчивостью к эрозии, коррозии, механическому износу, нагреву [1]. Однако технология получения таких труб при всей её перспективности нестабильна и её широкое внедрение невозможно без проведения работ по её оптимизации.

Разработке оптимальной методики получения покрытия, удовлетворяющего эксплуатационным требованиям, будет способствовать создание математической модели процесса нанесения внутри-трубного покрытия методом центробежного СВС, которая бы учитывала всё множество теплофизических и физико-химических параметров, формирующих это покрытие.

В работе [2] представлена методика, использовавшаяся для моделирования теплообмена меж- ду стенкой трубы и смесью для СВС в процессе прохождения фронта горения вдоль трубы. В процессе моделирования предполагалось, что в элементарном сечении слоя смеси для СВС происходит полное превращение реагентов. Однако как показывают исследования особенностей горения конденсированных систем с тугоплавкими продуктами реакции [3], а также изучение образования волны горения в системах с распределенной функцией скорости тепловыделения [4], такое предположение следует уточнить, поскольку скорость распространения фронта горения принципиально связана с неполнотой превращения вещества.

Перепады температур в сечении, перпендикулярном поверхности контакта слоев, очень малы, поэтому можно считать, что температурное поле гетерогенной системы смеси для СВС одномерно. В зоне реакции содержится очень много мелких частиц, что позволяет усреднить тепловые характеристики и в некотором приближении рассматривать смесь как гомогенную. Ширина зоны химической реакции в волне горения больше размеров частиц, которые можно представить как точечные источники тепла. Это позволяет свести задачу о распространении пламени горения в гетерогенной системе к классической [3].

В настоящей работе теплофизические характеристики системы рассматриваются с учётом того, что реагенты плавятся и образуют в волне горения жидкий продукт. Появление жидкой фазы увеличивает скорость горения и приводит к реакционной диффузии реагентов. Реагенты могут плавиться как в зоне прогрева волны горения, так и в зоне реакции. Поэтому по температурному профилю волны горения можно установить протяженность жидкой фазы при известной температуре плавления реагентов, а также время пребывания ее в жидком состоянии. Под действием центробежных сил произойдет дифференциация компонентов жидкой фазы. Время перераспределения частиц по массе связано со временем пребывания в жидком состоянии продуктов горения смеси для СВС. В данном случае имеет место гетерогенный расплав, в котором взаимно нерастворимые металлическая и оксидная фазы имеют разные плотности. В таком расплаве под действием центробежной силы происходит фазоразделе-ние – тяжелая фаза (металл) оседает на стенку трубы, легкая (оксиды) «всплывает» [5]. На этот процесс оказывает влияние температурное поле. При остывании увеличивается вязкость расплава и уменьшается скорость движения капель металла. Если время пребывания расплава в жидком состоянии больше времени фазоразделения, то оно успеет произойти. Полученное покрытие будет иметь хорошо разграниченные фазы: ближе к стенке трубы – металлическую и дальше от стенки – оксидную.

В процессе формирования внутритрубного покрытия методом СВС-металлургии по длине трубы образуются три области: сухой смеси СВС (порошка), жидкой и твердой фаз покрытия. По радиусу трубы имеются слои: стенка трубы, покрытие с подвижными границами фазовых переходов, порошок, жидкая и твердые фазы.

В целом установку для нанесения внутри-трубного покрытия можно представить цилиндрическим объектом послойной структуры как по радиусу, так и по длине, и использовать методику математического моделирования термокинетических процессов, приведенную в работах [6, 7].

В процессе настоящей работы в основу математического моделирования положены следующие допущения: толщина слоя смеси СВС постоянна по радиусу и по длине трубы; размер частиц смеси СВС намного меньше зоны реакции, что позволяет гетерогенную среду представить гомогенной; теплофизические параметры сред постоянны и не зависят от температуры; фронт волны горения распространяется в режиме устойчивого, стационарного горения с постоянной скоростью.

С учетом принятых допущений уравнения энергии для стенки трубы, смеси, химической кинетики, начальные и граничные условия примут вид:

ат_          „.      „  „.    d² т_

-^-Хет, s 1 ( T ^ 1 ^{- Т} ет) ^{+ Х}а,™^{( Т} ем ^- Ta) ⁺ aa "Г ;

д Т..      д Т..

-г м ■ ' Т = Х ем,ет ( Т _ст — Т ем ) + Х ем, s ^2 — Т ем ) + d t o x ’                    ’

<

_E д2Тсн  Q(Sk0) e RTeм , x

+ a ем —1м +       ⁰ -----Ф( п );

d x²        C p P

E

d n     d П zo 7 A

+ur — = (S^kn) e t г dx sa 0

I dt

R¹™ ф ( п );

Т т ( X , 0) = _ . ( X ); Т ем ( X , 0) = ^ ( X ); П ( X , 0) = - ( X ) (2)

Т ет (0, t ) = Ф cт ( t ); Т ем (0, t ) = Ф ем ( t ); n (0, t ) = Ф п ( t );

* A. дTCT^^,t) = «ет,ем(Тет(0, t) - Тем(0, t));(3)

a ^x

Т ем ^д T ^Cм (^{02 t} ) = « ем,ет ( Т ем (0, t ) - / , Ю. t )),

[          дx, ает, s 1p ет, s 1              ает,ем p ет,ем где Хет,s 1 =-------— ; Хет,ем =---------

P ет Сет S ет               р ет c ет S ет аем, s 2 p ем, s 2             аем,ет p ем,ет см,s см,s                 см,ст см,ст

Хем,s2              q ; Хем,ет р ем c ем S ем             рем cем S ем

Ф ⁽ п ) = ⁽1 -n ) y ;

Т_{s 1} , Т_{s 2} , T _см , T _ст – температуры внешней окружающей среды, внутренней окружающей среды, смеси и стенки;

« ет, s 1 , « ет,ем , « ем, s 2 , « ем,ет ^- коэффициенты теплоотдачи от стенки к внешней окружающей среде, от стенки к покрытию, от покрытия к внутренней окружающей среде и от покрытия к стенке;

p _{ст, s 1}, p _ст,см , p _{см, s 2}, p _см,ст – периметры раздела между стенкой и внешней окружающей средой, между стенкой и покрытием, между покрытием и внутренней окружающей средой и между покрытием и стенкой;

Р _ет , Р _ем — плотности етенки и покрытия;

c _ст , c _см – удельные теплоемкости стенки и покрытия;

S _ст , S _см – площади поперечного сечения стенки трубы и покрытия;

a _ст , a _см – температуропроводности стенки и покрытия;

и г - екороеть продвижения фронта горения;

Q – мощность источника энергии;

S_sa – удельная поверхность раздела реагентов;

k ₀ – предэкспоненциальный фактор;

Е – энергия активации химической реакции;

R – газовая постоянная;

П - глубина химичеекого превращения реагентов (0 < п <  1);

у – порядок;

Х _ст, Х _см - теплопроводность стенки трубы, покрытия.

Мощность источника энергии Q – тепловой эффект, полученный с помощью открытых баз данных FactSage , который рассчитывался как сумма средневзвешенных значений тепловых эффектов реакций алюминия с оксидами, присутствующими в составе смеси.

Для численного решения краевой задачи (1)–(3) использовали метод конечных разностей. Систему (1) представили в дискретном блочно-матричном виде:

где © m⁺¹

L =

T m” ^{+ 1} = AT m” — 1 + BT m” + CT m” + 1 + DT m” + ET_S +© ,   (4)

_ rp ” + 1 где Tm

n

^Tm — 1 =

A =

A ₁ 0 0

Гр ” + 1

Tстm т ”+1

см m

” ^{+ 1}

.11 m       J

n

^Тст m — 1

ⁿ см m — 1

.n m — 1

A 2

	T n , ст m + 1		T ” ст m
- T ”  = ; T m + 1	n см m + 1	■ Tn = ; m	n см m
	|_П m + 1 J		|_П m J

;

^Ts 1

^Ts 2 0

■ т = ; _s

E =

;

T 1 ” ^{+ 1}

rp ” + 1

T ₂

” + 1

^Tm — 1

” + 1

Tm

E

;

n

m

; M =

E

F = B + D;

T1n n T2

n

^Tm — 1

n T_m

;

T s

T s

;

T 5

T

5 J

H 11	H 12			0
A	F	C		0
0		A	F	C
0			Hm 1	H m 2 _

;

E

E

;

H 11 = A ■ 1 11 + F ; H 12 = A ■ 1 12 + C ;

H m1 = A + C ■ 1 21 ; H m 2 = F + C ■ 1 22 ;

A 3 _

;

B =

B 1 0 0

B 2 0

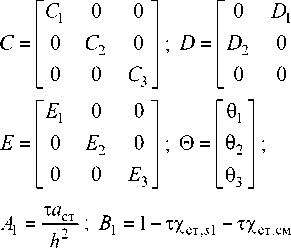
— г _ т a ст .

С ' = I²"^;

B 3 _

D 3

;

;

2 т а _ст h 2    ;

^D 1    ^тХ ст,см ; ^E 1    ^тХ ст, 5 1 ; ® 1    ⁰ ;

Д ^T a см ™г _R 1

A2 = —см + "ТГ; B2 = 1 — тХ h2    2h

т a,

см,ст

—

^тх см S 2

—

^{2 т} a ст .

h2

;

I 1 =

I 12 =

1 11 =

= T aсм - IHt •     = tv -              '

С 2      ₁ r>i ; ^D 2     ^тХ см,ст ; ^E 2     ^тХ см, s 2 ;

h ²       2 h                  ^{,                   ,}

^ = Q ( S_S a k 0 ) e

2         cp P

E RT см —ф ⁽ п );

TH

A3 = —; B = 1 — Ssakoe

3              3           sa 0

2 h

E

RT: " . С = _—12 г _;

3      2 h

D 3 = 0; Е 3 = 0; О 3 = т S_S a k 0 e

E

RT™ ф ( п ).

С учетом дискретных начальных и граничных условий (2), (3) система (4) примет вид:

I ₁₁

I 21 0

—

;

I 22 =

Ib =

I ₁₂

I 22 0

;

;

I 21 =

;

² h ^а ст,см

² h ^а см,ст ^ см

² h ^а ст,см

—

² h ^а ст,см

—

² h ^а см,ст ^ см

² h ^а см,ст ^ см

—

² h ^а ст,см

² h ^а см,ст ^ см

;

.

Результаты теплофизического моделирования [2] и построенная в ходе настоящей работы модель термокинетики процесса формирования внутритрубного покрытия были использованы для создания (на языке C#) программы для ЭВМ, которая позволяет прогнозировать результаты проведения процесса в различных режимах. Интерфейс программы позволяет в широких пределах изменять значения термокинетических, механических и геометрических параметров процесса.

П рим е ры ре з у л ьтатов та ко го м оде л иров а н ия представлены на рис. 1–3. Ис пол ьз ов анные исх одные параметры при в одятся в та б л и це .

Результаты компьютерного моделирования динамики формирования внутритрубного СВС-покрытия показывают, что в начальных сечениях трубы степень выгорания смеси СВС мала вследствие низкой температуры стенки трубы и порошка смеси. В результате не произойдет фазо-разделения в жидком состоянии и, как следствие, не будет сформировано полноценное покрытие. Отсюда следует вывод о том, что воспламенение

Исходные данные

П а ра м е тры			Стенка (сталь)	Порошок
Теплофизические	Плотность ρ , кг/м3		7800	4000
	Те пл ое м кос ть c, Дж/кг·К		500	1000
	Те пл оп ров однос ть a, Вт/К·м		47	1
	Те пл оп ере да ча α, Вт/К·м2	внешняя среда	1000	1000
		труба/смесь	1000	30000
Геометрические	Вн ешн и й ра д иус тр уб ы R 1, м		0,15	–
	Вн утренн и й ра д и ус тр уб ы R 2 , м		0,145	0,145
	Р а ди ус с л оя с м е си С ВС R 3, м		–	0,095
	Пе рим е тр ра з де л а сред, м	внешняя среда	0,9425	0,599
		труба/смесь	0,911	0,911
	Пл оща дь с е че н ия S , м2		0,0046	0,0375
Механические	Ск орость в ра ще н ия ω, об/мин		2000	2000
	Ск орость горе ния υ, cм/с		–	1
Кинетические	У де л ьн ая п ов ер х н ост ь раздела реагентов, м2		–	0,1
	Пр е д э кс пон е н ц иал ь н ый ф а к тор k		–	1
	Э н ерги я а к ти в а ц и и, Д ж / м оль		–	1000

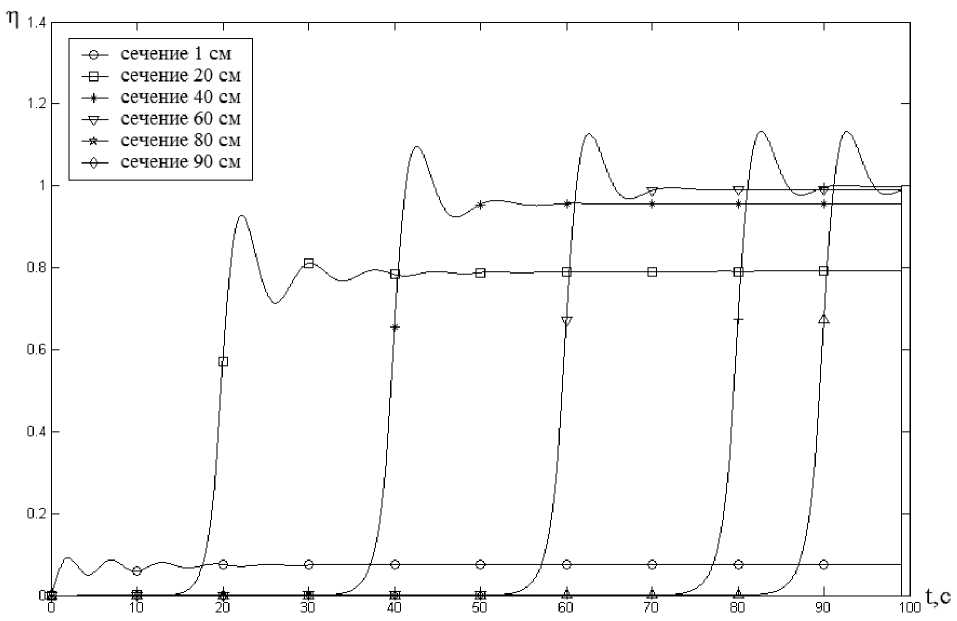
Рис. 1. Распределение степени выгорания смеси СВС по сечениям

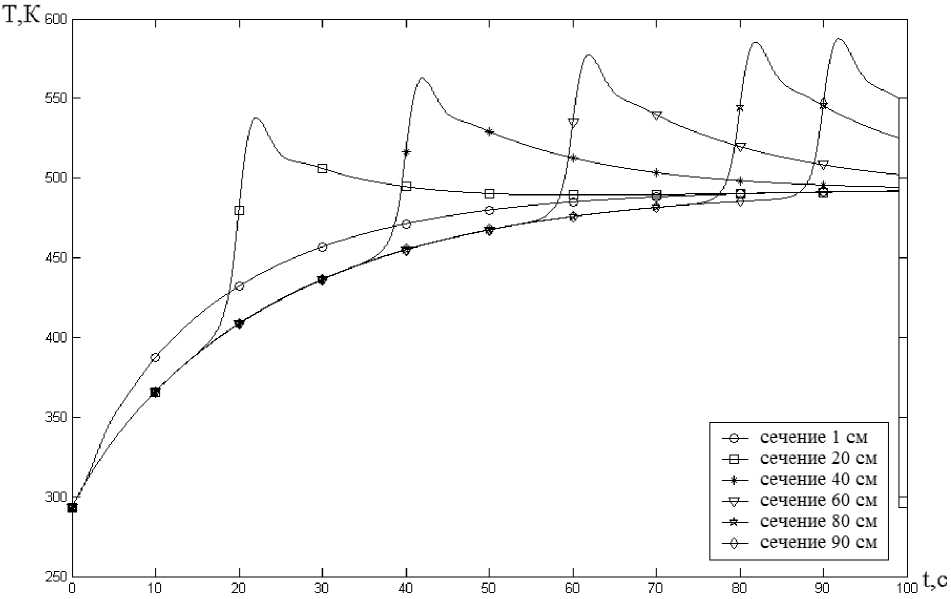
Рис. 2. Распределение температуры в стенке трубы по сечениям и времени

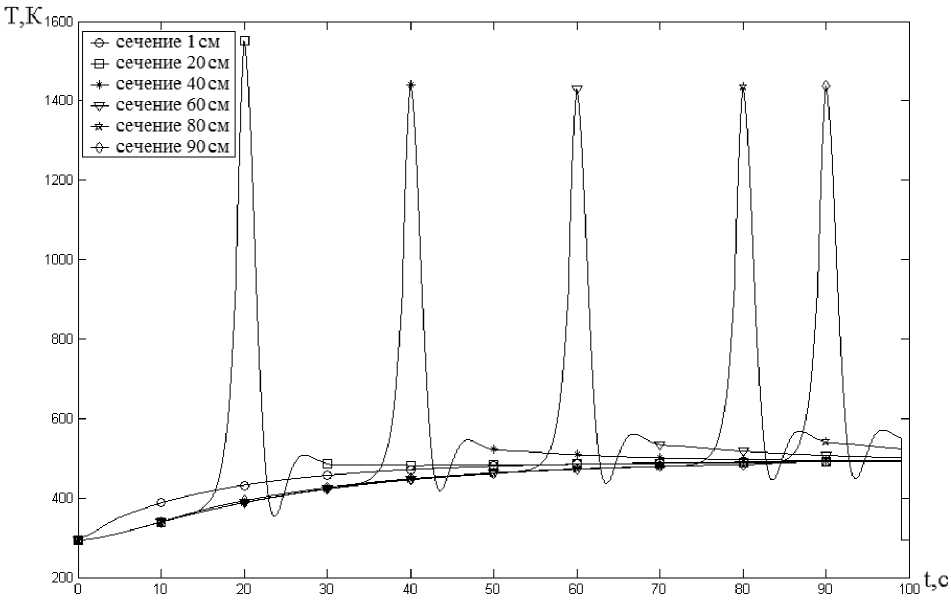
Рис. 3. Распределение температуры смеси СВС по сечениям и времени

см е с и с л е д ует произ в од ить не в н ул ев ом с е че нии тр убы, а в некотором опти м а л ьном , чтобы обе с печ и ть форм иров а ни е ка че стве нного покрыт ия в начальных сечениях.

Часть работы, связанная с термохимическими расчётами процесса СВС, выполнена при поддержке РФФИ, грант № 13-08-00545.

Садыков Р.А., Потапов В.И., Любимова А.А., Трофимов Е.А.