Моделирование распределения воды стационарными системами с дождевальными аппаратами кругового действия при расположении позиций по углам прямоугольника и ромба

Введение. В технике наблюдается тенденция замены натурных испытаний машин имитационным моделированием на компьютере. Адекватность имитационных моделей повышают использованием вероятностных характеристик случайных параметров, полученных по результатам простых опытов. Более сложные ситуации моделируются программой.

Испытание дождевальных систем выполняют по межгосударственному стандарту ГОСТ ИСО 7749-22004 либо по стандарту ассоциации испытателей СТО АИСТ 11.1-2010: Испытания сельскохозяйственной техники. Машины и установки дождевальные. Методы оценки функциональных показателей.

Опыт применения стандарта ГОСТ ИСО 7749-22004 показал его преимущества и недостатки.

Положительным является использование радиального метода испытания вращающихся аппаратов, позволяющего уменьшить трудоемкость и затратность натурных испытаний. Обработка результатов экспериментов предполагает моделирование перекрытия зон дождевания и вычисление показателя равномерности по Христиансену. В этой части открывается возможность для использования современных вычислительных машин и систем компьютерной математики [1, 2].

Недостатком стандарта является ограничение его действия на стационарные системы дождевания. Дождевальные аппараты вращательного действия устанавливаются на машинах поступательного и вращательного движения. Оценить пригодность испытанных аппаратов для таких машин тоже необходимо.

Сущность радиального метода испытания аппаратов состоит в следующем. Опыт проводится при отсутствии ветра. Стояк с дождевальным аппаратом устанавливают вертикально на заданной высоте. Дождемеры устанавливают на одном из радиусов на равном расстоянии друг от друга. Верх дождемеров выравнивают по горизонтали. Аппарат отводят от линии дождемеров так, чтобы при его включении вода в дождемеры не поступала. Далее аппарат вручную поворачивают равномерно до прохода линии дождемеров и прекращения попадания воды в дождемеры. Определяют количество воды в каждом дождемере взвешиванием или измерением объема мензуркой. По результатам опыта вычисляют интенсивность дождевания в каждом дождемере и строят график I(р) зависимости интенсивности от радиуса, который далее используется при моделировании распределения воды.

Моделирование распределения воды по зачетной площадке выполняют при размещении четырех аппаратов, идентичных испытанному, по углам квадрата со стороной А. Площадь, ограниченную линиями, соединяющими точки расположения аппаратов, используют в качестве зачетной при вычислении равномерности дождевания. Размер стороны квадрата принимают целым числом, тогда зачетную площадь делят на метровые квадраты, количество которых равно А×А. Точку в центре каждого квадрата соединяют с точками расположения аппаратов и измеряют радиусы. По графику I(p) находят интенсивность дождевания от каждого аппарата. Интенсивности складывают. После перебора всех метровых квадратов получают матрицу интенсивностей, по которой вычисляют показатель равномерности дождевания по Христиан-сену [3, 4, 5].

Недостаток метода состоит в применении ручных операций интерполирования и суммирования ин- тенсивностей. Кроме того, использование при моделировании только четырех аппаратов не позволяет найти оптимальную расстановку аппаратов. Способ моделирования по четырем аппаратам применим только при расстоянии между аппаратами, равном или большем радиуса орошения одного аппарата (рисунок 1 а). В этом случае на зачетную площадку попадает одна четвертая часть расхода от каждого аппарата. Вода от других аппаратов на зачетную площадку не попадает и коэффициент полноты учета равен единице. Если радиус орошения больше размера зачетной площадки (рисунок 1 б), то часть воды от каждого аппарата выходит за пределы зачетной площадки [6, 7]. Коэффициент полноты учета становится меньше единицы. Оценивать равномерность только по части воды на зачетной площадке не рационально, рекомендации по повышению равномерности могут быть ошибочными.

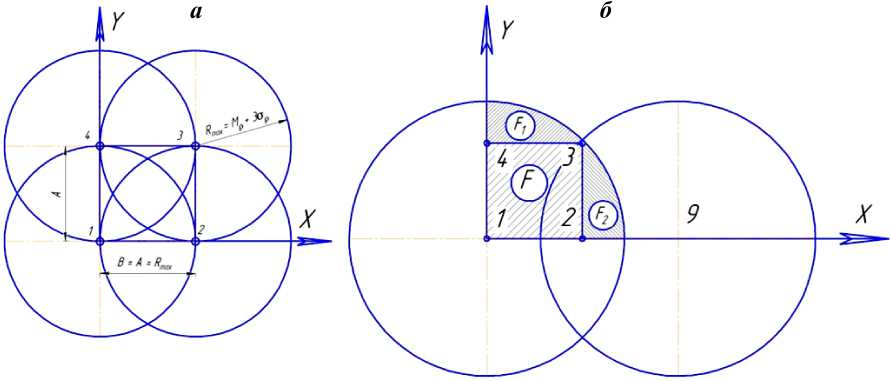
Рисунок 1 – Схемы перекрытия зон дождевания

Моделирование дождевания по четырем позициям может дать результат, на основании которого делается вывод о неудовлетворительной равномерности распределения. При увеличении перекрытия необходимо моделировать работу аппаратов из соседних рядов. Например, по рисунку 1 б площадка F 2 компенсируется от аппарата, работающего на девятой позиции.

Цель исследования. Выполнить математическое моделирование распределения воды вращающимися дождевальными аппаратами при их расположении по углам квадрата и по углам ромба. По результатам моделирования получаем матрицу доз дождевания и по матрице доз вычисляем равномерность орошения.

Методика исследования. Составлены программы моделирования распределения воды стационарными аппаратами кругового действия с двенадцати позиций (рисунок 2). При расположении позиций по углам квадратов или прямоугольников (рисунок 2 а) первый ряд совпадает с осью X, второй – смещен по оси Y на расстояние А, третий – смещен на расстояние 2А, четвертый – на расстояние минус А. Расстояние в ряду между позициями обозначено буквой В. Зачетная площадка размером А×В расположена между первым и вторым рядами. Начало зачетной площадки обозначено Xo. Задавая параметр Xo вектором, анализируем изменение равномерности вдоль рядов. Максимальный сдвиг по Xo при двенадцати позициях принимаем не более двух расстояний между позициями.

Ромбическое расположение позиций показано на рисунке 2 б . Если рассматривать только первый и второй ряды, то расположение позиций – треугольное. Это то, что рекомендует стандарт СТО АИСТ 11.12010. При А = 0,866·В получаем равносторонние треугольники. Если рассматриваем четыре ряда позиций, то расположение их называем ромбическим. В соседних рядах позиции смещены в направлении оси X на половину расстояния В .

Задача данного исследования – оценить преимущества и недостатки прямоугольного и ромбического расположения позиций.

Если аппарат находится в центре системы координат XOY и работает по кругу, то положение площадки dF задаём в прямоугольных и в полярных координатах. Вероятность попадания жидкости на элемен- тарную площадку dF , выделенную в зоне дождевания двумя радиусами с углом между ними d и двумя окружностями с приращением радиуса dр, определится как произведение вероятностей попадания в диапазон угла d и радиуса d , т.е.

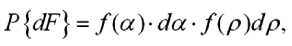
где f (  ) – плотность вероятности угла расположе ния струи;

f( ) – плотность вероятности дальностей полета капель.

Интенсивность дождя на площадке равна количеству воды, попадающей на неё в единицу времени, деленному на её площадь, При независимых и имеем:

I

Q f( ) d f( ) d Q f( ) f( ) dd

Доза полива любой площадки стационарным аппаратом определяется произведением интенсивности на продолжительность времени работы аппарата.

Равномерность по Христиансену вычисляем по матрице доз на зачётной площадке MDi,j . По матрице доз вычисляем среднее значение элементов матрицы M mean( MD) . Далее считаем линейные отклонения элементов матрицы от среднего, взятые по модулю — 1 = / —D - — /, и вычисляем среднее значение элементов матрицы разностей М1.

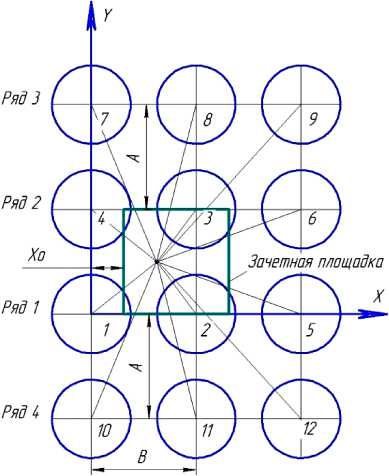
Рисунок 2 а – Схема расположения позиций по углам прямоугольников

Плотность вероятностей дальностей полёта капель от аппарата с двумя соплами определяется суперпозицией двух нормальных распределений [8, 9, 10].

Позиции аппаратов расположены рядами. Моделируем работу аппаратов на двенадцати позициях (рисунок 2). На рисунке зоны дождевания показаны условно.

Равномерность по Христиансену вычисляем по формуле

(   mean М 1 i

CDU = 100  1- mean- --- .    (2)

M

Аппарат вращается равномерно, поэтому плот- ность вероятности угла расположения струи определяется по формуле f («) =

2-л"

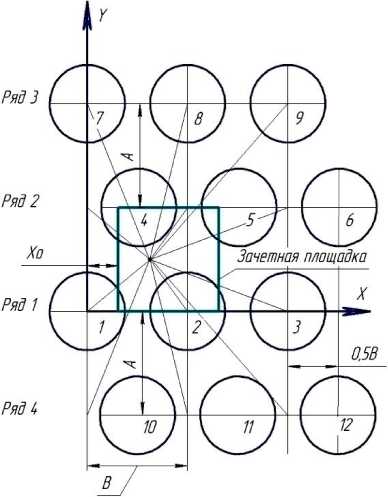
Рисунок 2 б – Схема расположения позиций по углам ромбов

Координаты точек установки аппаратов приведены в таблице.

Зачетная площадка для вычисления равномерности расположена между рядами позиций и имеет ширину, равную А . Длина зачетной площадки принята равной В . Начало зачетной площадки имеет координату Xo . Параметры А и В принимаем целыми. Тогда зачетную площадку делим на метровые квадраты и в центре каждого квадрата вычисляем дозу орошения.

Координаты позиций аппаратов

Номер аппарата, u	Координаты позиций аппаратов по рисункам 2 а и 2 б
	X u по рисунку 2 а	Y u по рисунку 2 а	X u по рисунку 2 б	Y u по рисунку 2 б
1	0	0	0	0
2	В	0	В	0
3	В	А	2В	0
4	0	А	0,5В	А
5	2В	0	1,5В	А
6	2В	А	2,5В	А
7	0	2А	0	2А
8	В	2А	В	2А
9	2В	2А	2В	2А
10	0	- А	0,5В	- А
11	В	- А	1,5В	- А
12	2В	- А	2,5В	- А

Блок-схема алгоритма вычисления матрицы доз орошения на зачетной площадке изображена на рисунке 3. По матрице доз вычисляется коэффициент равномерности по Христиансену и коэффициент полноты учета. Программы KePr2S12( A, Xo ) и KeRb2S12( A, Xo ) работают по аналогичным алгоритмам. Отличие их состоит в вычислении расстояний от метрового квадрата до аппаратов. В первой программе расстояния вычисляются с использованием координат аппаратов по рисунку 2 а , а во второй – по рисунку 2 б . Исходные данные для расчета задаем в имени программы и в её начале. Перечень исходных и вычисляемых данных для работы с программой:

Q – расход воды через аппарат, л/с;

T – продолжительность работы аппарата на позиции, с; M р₁ – математическое ожидание дальности полета струи от основного сопла, м;

СУ р1 – среднее квадратическое отклонение дальности полета струи от основного сопла, м;

M р₂ – математическое ожидание дальности полета струи от дополнительного сопла, м;

M р 1   10 м ; О"р 1   3 м ;

– среднее квадратическое отклонение дальности полета струи от дополнительного сопла, м;

C – весовой коэффициент основного сопла;

C – весовой коэффициент дополнительного сопла;

А – расстояние между рядами аппаратов по оси Y , м;

В – расстояние между позициями аппаратов по оси X , м;

X i , Y j – координаты метрового квадрата на зачетной площадке;

u – номер аппарата;

р _u – расстояние от центра метрового квадрата до u -того аппарата, м;

D_u – доза орошения от u -того аппарата;

CDU – коэффициент равномерности дождевания;

К _у – коэффициент полноты учета воды на метровом квадрате.

Результаты моделирования и их обсуждение. В примере расчета приняты следующие исходные данные:

M 5 м ; а_р   1,5 м ;

C 0,8; C 0,2; Q 2 л / с ; T 2000 c .

Программа вычисляет дозы дождевания на метровых участках зачетной площади и по матрице доз – показатель равномерности дождевания по Христиансену и коэффициент полноты учета. Если коэффициент полноты учета близок к единице, то учитывается вся вода, выбрасываемая одним аппаратом за время дождевания. Результат счета выводится в виде вектора из двух строк. В первой строке – показатель равномерности по Христиансену, во второй – коэффициент полноты учета. Задавая параметр Xo в виде вектора при разных значениях параметра A , получаем матрицы: M, M 1 и M 2 (рисунок 4).

По матрицам построены графики.

По агротехническим требованиям распределение считается равномерным, если коэффициент Хри-стиансена не менее 80%. Такой результат достигнут при А = 20 м и Xo в диапазоне от нуля до 29 м. График равномерности очень устойчив к сдвигу зачетной площадки. Только при Xo > 30 м равномерность ухудшается, что связано с выходом зачетной площадки за пределы зоны дождевания пятой и шестой позиций. Если позиции наращивать в направлении оси X , а ряды в направлении оси Y , то равномерность будет более 80%, что позволяет сделать заключение о возможности равномерного орошения всего поля.

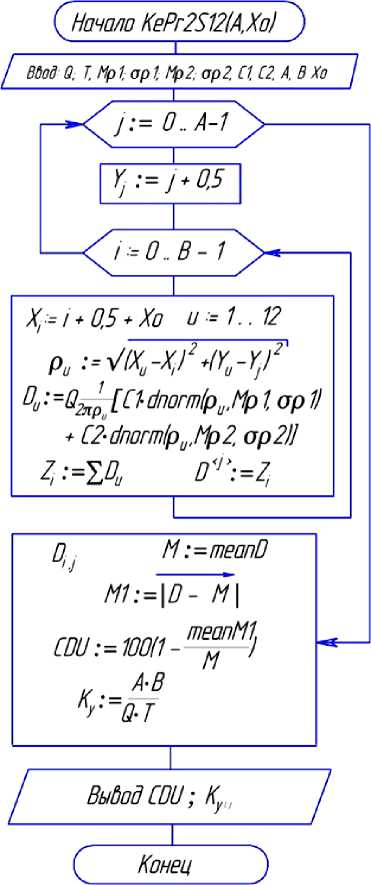
Рисунок 3 – Блок-схема алгоритма моделирования распределения воды аппаратом кругового действия при прямоугольном расположении позиций

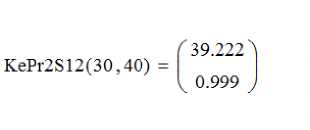
j:=0..40 Xoj := j M^ := KePr2S 12(20,Xoj)

Ml^ := KePr2S 12(25,Xoj) M2^ := KePr2S 12(30,Xoj)

	0	1	2	3	4	5
0	84.75	84.751	84.751	84.752	84.752	84.752
1	0.999	0.999	0.999	0.999	0.999	0.999

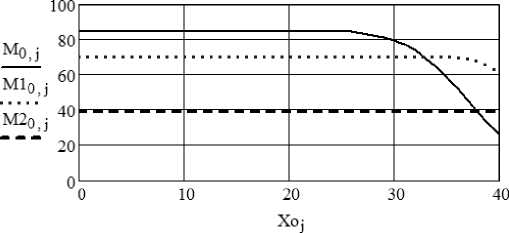
Рисунок 4 – Результаты счета равномерности распределения воды при А = 20, 25 и 30 м и Xo = 0–40 м

При А = 25 и А = 30 м агротехнические требования не выполняются, равномерность более 80% не достигается.

Программа KeRb2S12( A, Xo ) позволяет оптимизировать параметры позиционирования аппаратов по критерию равномерности дождевания при ромбическом расположении позиций.

Результат счета показан на рисунке 5.

При А = 20 м равномерность более 80% только при Xo = 0–2,5 м. При других значениях Xo равномерность волнообразно изменяется. Минимум равномерности около 50% при Xo = 18 м. При таком значении расстояния между рядами распределения явно хуже, чем при прямоугольном расположении позиций. Только при уменьшении расстояния до А = 10 м диапазон допустимых значений Xo увеличен до 20 метров.

Xoj := j

M^ := KeRb2S12(10,Xoj)

Ml^ := KeRb2S12(20,Xoj)

M2^ := KeRb2S12(30,Xoj)

I 0.963

0 1 2 3 4 5 0 83.889 84.042 83.409 81.96 79.728 76.939 1 0.963 0.975 0.985 0.991 0.995 0.997 j := 0..40

( 83.889

KeRb2S12(20,0) =

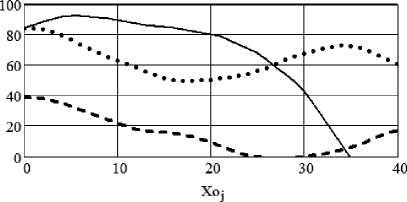
Рисунок 5 – Результаты счета распределения воды аппаратами кругового действия при расположении позиций по углам ромбов

Если в программах KePr2S12( A, Xo ) и Ke Rb2S12( A, Xo ) удалить девять последних команд и вместо них вставить D , то программы выводят матрицу доз орошения на зачетной площадке.

Выводы

• 1.    Программы KePr2S12( A, Xo ) и KeRb2S12( A, Xo ) моделируют распределение воды аппаратами кругового действия при расположении позиций по углам прямоугольников и по углам ромбов. Результаты счета выводятся в виде матрицы доз или в виде матрицы из двух строк. В первой выведен коэффициент равномерности по Христиансену, во второй – коэффициент полноты учета.

• 2.    Размещение позиций по углам квадратов при А = 20 м обеспечивает получение равномерности более 80% в диапазоне зон орошения. Наращивание позиций в направлении оси X и рядов в направлении оси Y позволяет сделать вывод о возможности равномерного орошения всего поля.

• 3.    Ромбическое размещение позиций аппаратов не имеет преимуществ перед расположением по углам квадрата. При расстоянии между рядами позиций А = 20 м равномерность менее 80% уже при Xo > 2,5 м и волнообразно снижается до 50% при Xo = 18 м. Только при А = 10 м диапазон допустимых значений Xo расширяется.