Моделирование распространения короткого двумерного импульса света

Задачи моделирования процессов распространения электромагнитных волн в различных средах были и остаются актуальными в связи с широким практическим применением различных оптических устройств: световодов, волноводов, ДОЭ. Численное моделирование прохождения света в среде позволяет решать как прямые задачи (расчёт электромагнитного поля в некоторой области), так и обратные (подбор параметров ДОЭ для формирования заданного распределения интенсивности).

Сам процесс распространения волны может описываться различными способами. Наиболее общее представление даёт система уравнений Максвелла. Однако их решение – трудоёмкий процесс. Вторым наиболее распространённым вариантом является применение волнового уравнения. В случае, когда не интересует временная динамика процесса, а требуется рассчитать стационарное электромагнитное поле, используют уравнение Гельмгольца или уравнение Шрёдингера.

Для каждой физической модели применяется свой численный метод расчёта. Так, для уравнений Максвелла характерно применение метода FDTD [1], [2]. Данный метод реализован, например, в коммерческом пакете FullWave компании RSoft. Для случая решения уравнения Гельмгольца или уравнения Шрёдингера применяют метод BPM, который реализован, например, в коммерческом пакете BeamProb компании RSoft [3]. Применяют и различные гибридные методы, к примеру, для решения однонаправленного волнового уравнения используют метод TD-BPM [4] - [6].

Отдельно стоит отметить большой интерес к вопросу моделирования прохождения ультракоротких импульсов через различные оптические системы [7] - [9]. Современные лазеры способны генерировать световые импульсы длительностью несколь- ко циклов оптического поля [10] - [11], обеспечивая инструменты для контроля самых быстрых движений атомов в молекулярных системах.

В данной статье рассматривается процесс распространения ультракороткого импульса в планарном волноводе, в основу описания которого положено волновое уравнения. В первой части для первой краевой задачи в общем виде с помощью метода разделения переменных находится аналитическое решение. Во второй части производится построение явной конечноразностной схемы и сравнение численных решений, рассчитанных с помощью разработанной схемы и коммерческого пакета FullWave, и аналитического решения. В третьей части проводится моделирование процесса прохождения ультракороткого импульса через тонкую плёнку. Сравниваются теоретические и расчётные коэффициенты отражения и преломления.

1. Аналитическое решение

Общий случай

Рассмотрим следующую краевую задачу для волнового уравнения в двумерном пространстве [11]:

д ² E y    1

"ат5" - П? A xzEy = f(x, z,t), xG(ax;bx), zG(az;bz), tg(aт;bt];

^eA =Ф 1 ( ^z , ^t ) , ^{z G} ( a z ; b z ) , ^tg ( a т ; b t ] ; x = a x

EA, _b ^ 2 ^{( z} , ^t) , ^{z g(} a z ; b z ) , ^tg ( a т ; b t ] ; I x = b x

^{< E} y|_z = a =^ i ( x , ^t ) , x ^G ( a x ; b x ) , ^tg ( a т ; b t ] ; ⁽¹⁾

E yY = b =^ 2 ( ^x , ^t ) , ^{x G} ( a x ; b x ) , ^tg ( a т ; b t ] ;

EyV =Xi(x,z), xG(ax;bx), zG(az;bz); t=aт dE           , x

"дт" =X 2 ( ^x,^z ) , ^{x G} ( a x ;b x ) , ^{z G} ( a z ;b z ) , t= a. т

Л д2 , д2

где А„ =—7 + —х - оператор Лапласа, Ev - проек-12 дх2 д z2 y ция вектора напряжённости (ТЕ-поляризация) электрического поля на ось у, В/м; n - коэффициент преломления; х и z - пространственные координаты, м; т = ct - аналог времени распространения, м; t - время, с, с - скорость света, м/с; [ax; bx] и [az; bz] - границы расчётной области в пространстве, а [aT; bT] -во времени, пары функций ф1(z, т) и ф2(z, т), а также и у1(х, т) и у2(х, т) - граничные условия, а х1(х, z) и Х2(х, z) - начальные условия, f (х, z, т) - функция источников.

Для её решения перейдём к краевой задаче с однородными краевыми условиями, используя следующие замены:

E y ( х , z , т ) = Е ( х , z , т ) + U ( х , z , т ) + V ( х , z , т ) ;

^{U ( х} , z , ^Т) = Г ^ ( V 1 ^{( х} , ^Т) " V L= a. ) ⁺ I                b z- a z

\ ^ ^ ( ^ ^{( х} , ^т)- V z = b z ) ^;

, х ( Ь _х - х ) . . ( a _x - х ) . . V ( ^х , z , ^т ) = ----- Ч ( z , ^т ) + ^----- ю_; ( ^z , ^т ) .

Ь - a_r         a_r - Ь

Стоит отметить, что должно выполняться условие согласованности граничных функций:

U (ах,z, т) = U (Ьх,z, т) = 0.

После подстановки выражений (2) в систему (1) получим:

д2 E   1 Л сА

• ^- n А xz ^E = f ^{( х} , z , ^т) ,

• ^{х G} ( a ; ^Ь х ) , ^{z G} ( a z ; b z ) , M a т ; ^Ь т ] ;

• ^E L= a_x = ^E L = Ь х = ⁰ z ^G a z ; ^b z ) , ^TG( a т ; ^Ь т^{] ;}

E\z=az = E\z = . = 0 х G( ах ; Ьх ) , Ma т ; ЬтЬ

E L- a = ^х ( ^х , ^z ) , ^{х G} ( ^а х ; ^Ь х ) , ^{z G} ( ^a z ; ^Ь ₂ ) ;

_{д Е} "^т

"дт     = Z- (х,z), х G( ах; Ьх), z G( az; Ь2), т=ат

E ( х , z , т ) = ]Г j L;7 ;_m ( т ) X, ( х ) Z _m ( х ) ;

.=1 m =1

• < X_t ( х ) = cos а , а _х • sin а , х - sin а , а _х • cos а , х ;

^Zm ( ^z ) = ^cos Р m ^a z • ^sin P m z ^- sin P m ^a z ' ^COs P m z ;

T m ( ^т ) = ^C 1 ( ^т ) cos Y ,m ^{т+ C} 2 ( ^т ) sin Y ,m ^т ,

где     X , ( х ),     Z m (z ),     T im (т);     а _; =д / /( Ь _х - а _х ) ,

Р m = ^П ml ( ^Ь z ^{- a} z ) , Y im = V ^{а 2 +} P m,/ ^{n -} собственные функции и собственные числа оператора Лапласа по переменным х, z и т, соответственно.

Коэффициенты С 1 (т) и С ₂(т) найдём с помощью метода неопределённых коэффициентов Лагранжа:

C 1 ( ^т ) = ^-—J F m ( ^т ) - ^sin Y im ^т - d ^{т +} C 1 ( ^а т ) ;

^Y im

^C 2 ( ^т ) = — J X ( ^т ) • ^COs Y im ^т • ^{d T + C} 2 ( ^a т ) ,

I            Y im"

bx bz

4 J J f (х, z, т) Xi (х) Zm (х) дх dz axaz im ( )            (Ьх - ах)(Ьz - az)

- коэффициенты разложения в ряд Фурье правой части уравнения системы (4); константы С 1 ( a _т ) и С ₂( Ь _т ) определяются из начальных условий.

Таким образом, решение исходной задачи представимо в следующем виде:

LM

^Е у ( ^х , z , ^т ) = ЕЕ ^T m ( ^т ) ^Xl ( ^х ) ^Z m ( ^х ) ⁺ i =1 m =1

+ U ( х , z , т ) + V ( х , z , т ) .

Частный случай

Рассмотрим планарный волновод, оболочка которого выполнена из материала, идеально отражающего излучение. В волновод подаётся импульс, но в начальный момент времени источник выключен. Запишем математическую модель представленной задачи:

^д 2 ^Е У ± f ^д 2 ^Е У +Х 1 дт ² n² д х^{2 +} д z²

V             7

где

f ( х , z , т ) =

= f ( х ,z,y-⁸2'^{V + U}. + A^zfc + U > ; дт           n

^{х G} V ^{- 1}"2> ; ⁱ 2 ) , ^{z G} ( 0; ^; z ) , ^TG ( 0; ^T ] ^;

Z 1 ^{( х} , ^z ) = X 1 ^{( х} , ^{z )-(} V ⁺ U )|_T_„ ;

^{1 т}= ^a т

„ , x , x д(V + U) %2 ( х, z ) = %2 ( х, z )-------- дт

.

т= a.

Ey\_x T = Ех = 1 х = ⁰, z g ( 0; ^; z ) , TG ( 0; ^T ] ;

^х = 2           2

Ey| _z = ₀ =^ ( ^х , ^т ) , ^{х g f- 1} 2; ⁱ 2 ¹ , ^TG ( 0; ^T ] ;

Ey|z = iz⁼ °’ ^{х G} V ^{- 1} 2; ⁱ 2 ¹ , ^TG ( 0; ^{T ]} ;

Используя метод разделения переменных Фурье, найдём решение краевой задачи (4):

E y | т=0

д Ey дт

т=0

= 0, х G

Г z z)

xx

V 2’2 7

z g ( 0; i _z ) .

где l_x и l_z – ширина и длина волновода (в метрах), соответственно, T – время моделирования (в секундах), ψ( x, τ) – напряжённость электрического поля на входе в волновод в момент времени τ, (В/м).

Зададим начальное условие следующим образом:

Представленная конечно-разностная схема обладает вторым порядком аппроксимации по всем шагам дискретизации, а также обладает следующим условием устойчивости:

V ( x , т ) = sin ®T- cos a 1 x ,

2n                            , где to =--несущая частота, рад/с;

% 0

λ 0 – длина волны в свободном пространстве, м. Найдём решение задачи (11) в виде ряда, воспользовавшись вышеизложенным методом:

M

E y ( x , z , т ) = ^ ( B sin toT+ C sin Y 1 _m т ) х m =1

х cos a 1 x sin в _m z ,

где C = - 2 ^{to( 1 +} A ) ; B = A ; A = ™’ n 2 ^-a 2,.

^в m l Y 1 m           ^в m l z          П 2 ( Т 2 „ "to 2 )

Стоит отметить, что полученный ряд является медленно сходящимся.

Заметим также, что частное решение (13) задачи было получено ранее и другими авторами [12, 13], в то время как решение (10) краевой задачи для волнового уравнения в наиболее общей постановке (1) получено впервые в этой статье, но с использованием известных методов.

2. Конечно-разностная схема

Построение конечно-разностной схемы

Построим на равномерной сетке явную конечноразностную схему [14]:

Л т E k = ^J2 Л _XI: k + ^2 Л _z E i , n

ij

n

ij

i = 1, I - 1; j = 1, J - 1; k = 1, K - 1;

h

n

2- [—+—) < 1. t21 hx2   h2 J xz

Сравнение аналитического и разностных решений

Для оценки практической сходимости численного решения, получаемого с помощью схемы (14), проводилось сравнение результатов моделирования с аналитическим решением, а также с результатами моделирования, полученными с помощью коммерческого пакета FullWave, в котором решаются уравнения Максвелла.

Стоит отметить, что вследствие медленной сходимости ряда (13) необходимо брать не менее М =900 членов ряда для получения приемлемой точности, которая характеризуется средней квадратичной ошибкой (СКО) 0,01% (максимальное отклонение 4∙10^-3 В/м, т.е. 0,4%) в сравнении с решением, полученным путём учёта 1500 членов ряда. В случае М = 300 погрешность характеризуется величиной в 0,3% (максимальное отклонение 0,01 В/м, т.е. 1%).

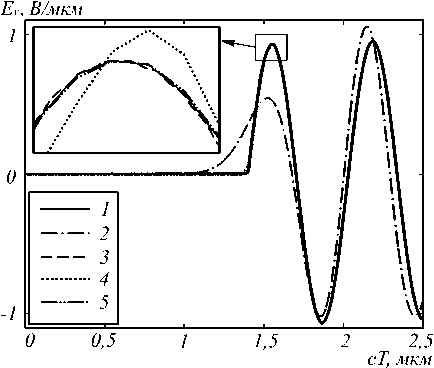
На рис. 1 приведены графики численных решений, полученных с помощью разработанной схемы и коммерческого пакета FullWave, в сравнении с аналитическим решением, полученным по формуле (13). Расчёты проводились для сеток, представленных в табл. 1, и при следующих параметрах: λ 0 = 0,633 мкм, l x = 3 мкм, l z = 10 мкм, n = 1, T = 9 мкм.

Таблица 1. Значения погрешностей

D	h x	h z	h τ
1	λ 0 /6,33	λ 0 /63,3	λ 0 /1266
2	λ 0 /6,33	λ 0 /633	λ 0 /1266

<

E ˆ _ik_j

E ˆ _ik_j

I i =0

I j =0

= E^ = I = 0, j = 1, J - 1, k = 2, K ;

=Vk,i = 17/-^ , k = 2^K;

I ? k    = 0, i = 1, I - 1, k = 2, K ;

ij _{j = J}

I:,k    = 0, i = 0, I , j = 0, J ;

ij _{k = 0}

I k =0

E k ^{+ 1}

-

E _ik_j

h т

k =0

= 0, i = 0, I , j = 0, J ,

где E _i ^k _j и

V i

ˆ

– сеточная функция, взятая в узле

( i , j , k ); Л Е i

E i +1 ^-

2 E? + л h2i   i 1 – разностный оператор

Лапласа; I, J, K – количество интервалов разбиения

llT по переменным x, z и т; hx = -у, hz = -J, hт = K шаги аппроксимации по переменным x, z и τ.

Рис. 1. Напряжённость электрического поля, рассчитанная аналитически (кривая 1), пакетом FullWave на сетке D = 1 (кривая 2) и сетке D = 2 (кривая 3), разностной схемой на сетке D = 1 (кривая 4) и сетке D = 2 (кривая 5)

Из графиков видно, что даже на достаточно крупной сетке схема (14) даёт совпадение порядка 99%, в то время как FullWave на аналогичной сетке даёт решение со смещением, вследствие чего совпадение характеризуется величиной лишь 10%. Однако на мелких сетках оба численных решения совпадают с аналитическим. СКО для численного решения, полученного с помощью схемы (14), составляет 0,014%, а для решения, полученного с помощью пакета FullWave, СКО = 1%.

Также численные эксперименты показали, что схема (14) менее чувствительна к величине шага по времени, нежели к величине шага по пространственной переменной z . Таким образом, для достижения эквивалентной точности предложенному методу требуются сетки меньшей размерности, нежели методу FDTD, реализованному в пакете FullWave, вследствие чего сокращается требуемый объём оперативной памяти и время расчёта самого решения.

Для схемы (14) было проведено численное исследование сходимости. Результаты исследования сходимости представлены на рис. 2 и в табл. 2, где D – номер сетки с соответствующими шагами дискретизации, а ξ – среднеквадратическая погрешность аппроксимации, %. Расчёты производились при вышеприведённых параметрах.

Таблица 2. Значения погрешностей

Зададим начальное условие следующим образом:

n x

V ( x , ^T ) = g up ( ^T ) ' g down ( ^T ) ' sin ® ^T ' cos—,       ⁽¹⁶⁾

l _x

где

и

g down ^(т)

g up ^(t) =

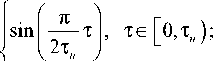
1, ^те ( ^т u , T ] ;

1, те [0,т,— тd);

I sinf П/

V

s

-

T]

A

2т d

те(т s-т d,т s ];

D	h x	h z	h τ	ξ, %
1	λ 0 /128	λ 0 /2024	λ 0 /2400	0,0053
2	λ 0 /64	λ 0 /1024	λ 0 /1200	0,0144
3	λ 0 /32	λ 0 /512	λ 0 /600	0,0382
4	λ 0 /16	λ 0 /256	λ 0 /300	0,0937
5	λ 0 /8	λ 0 /128	λ 0 /150	0,1837

– функции вхождения и затухания сигнала, τ u – время нарастания амплитуды сигнала; τ d – время спада амплитуды сигнала; τ _s – время подачи сигнала.

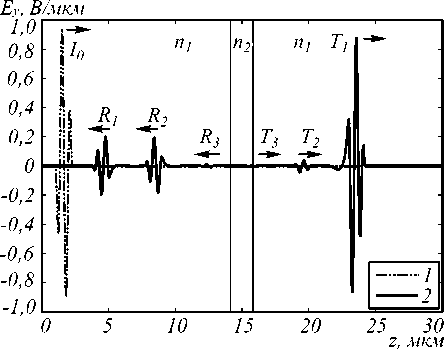
Расположим стеклянную пластинку шириной b на расстоянии a от источника. На рис. 3 представлена мгновенная картина амплитуды поля, полученная вследствие прохождения ультракороткого импульса через тонкую пластину. Расчёты производились при следующих значениях параметров: n 1 = 1, n 2 = 1,55, a = 14,367 мкм, b = 1,266 мкм, λ 0 = 0,633 мкм, l x =3 мкм, l z =30 мкм, T =9 мкм, h x = λ 0 /6,33 мкм, h z = λ 0 /633 мкм, h τ = λ 0 /1266 мкм, τ u = 0,633 мкм; τ d = 0,633 мкм; τ s = 1,266 мкм.

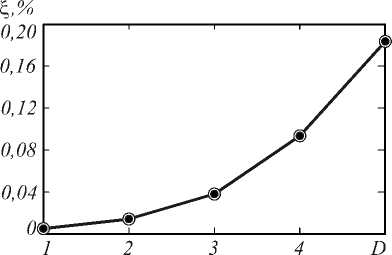
Риc. 2. Погрешность в среднеквадратической норме

Из приведённых выше результатов очевидна сходимость численного решения к аналитическому. Порядок сходимости близок к квадратичному.

3. Моделирование ультракороткого импульса

В настоящее время актуально исследование поведения в различных оптических системах коротких и ультракоротких импульсов. Смоделируем прохождение ультракороткого импульса через стеклянную плоскопараллельную пластинку, считая, что среда обладает мгновенным откликом (без учёта дисперсии материала).

Риc. 3. Мгновенная картина амплитуды поля на оптической оси в момент времени t = 88,898 фс для импульса длиной 4,223 фс: входящий импульс (кривая 1) и результирующее поле (кривая 2)

На рис. 3 можно наблюдать явление многократного отражения и прохождения импульса от поверхности плёнки, где I 0 – входящий импульс, R 1 , R 2 и R ₃ – отражённые импульсы, T ₁, T ₂ и T ₃ – прошедшие импульсы [15].

В табл. 2 приведены теоретические и расчётные коэффициенты отражения / пропускания для соответствующих отразившихся / прошедших волн, где ^ i и 3 i - коэффициенты отражения и преломления соответствующего i- го импульса.

Таблица 3. Коэффициенты для прошедших и отражённых импульсов
Тип импульса	Теоретические ℜ i / ℑ i	Расчётные ℜ i / ℑ i	Длина, фс
R 1	0,0465	0,0421	8,7494
R 2	0,0423	0,0430	10,3405
R 3	9,1563∙10-5	5,1596∙10-5
T 1	0,9091	0,9081	12,5554
T 2	0,0020	0,0021	13,3492
T 3	4,2601∙10-6	1,5996∙10-5
Всего	1	0,9953

Из таблицы видно, что результаты численного эксперимента хорошо согласуются с теорией. СКО составила 0,47%. Отражение и прохождение ультра- короткого импульса от тонкой пластины подчиняется законам Френеля. Также замечено уширение отразившихся и прошедших импульсов по сравнению с входным сигналом (четвёртый столбец табл. 3).

Известно, что при полном внутреннем отражении ультракороткого импульса происходит фазовый сдвиг, который приводит к изменению распределения интенсивности отразившегося импульса [16]. Смоделируем полное отражение ультракороткого импульса от границы раздела двух сред.

Пусть импульс падает на поверхность под углом θ. Расчёты производились при следующих значениях параметров: n ₁ = 1,5 , n ₂= 1, θ = 60 °, λ₀ = 0,633 мкм, l_x =6 мкм, l_z =6 мкм, T =6 мкм, h_x = λ₀/10 мкм, h z = λ 0 /422 мкм, h τ = λ 0 /528 мкм, τ u = 0,3165 мкм; τ _d =0 мкм; τ _s =0 мкм.

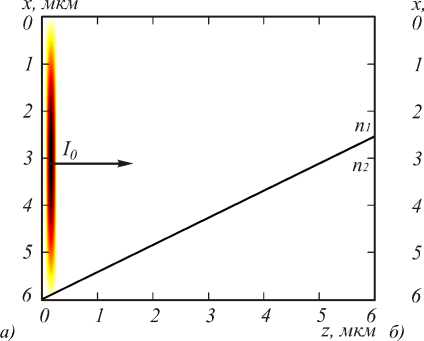
Риc. 4. Картина дифракции для импульса длинной 1 фс в момент времени: 1,3609 фс (до отражения) (а);

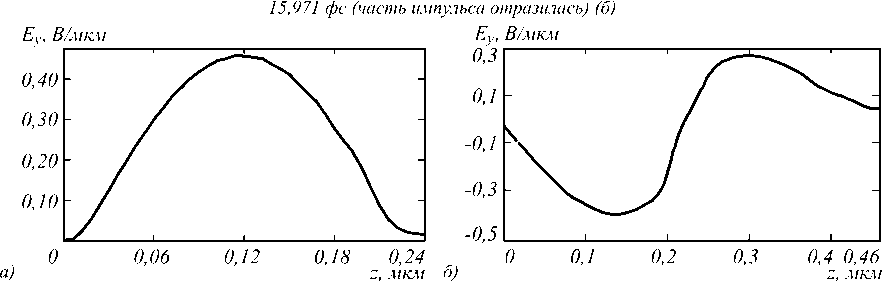
Риc. 5. Сечение импульса в момент времени 15,971 фс: падающего, I0 (а); отражённого, R (б)

На рис. 4 можно наблюдать явление полного внутреннего отражения от границы двух сред: оптического стекла и воздуха (граница представлена чёрной линией), где I ₀ – падающий импульс, R – отражённый импульс, а направление распространения импульсов указано стрелками. Из рис. 4 видно, что отражённый импульс исказил свою форму и состоит из двух «лепестков», вместо одного падающего «лепестка». Сравним распределения интенсивности падающего и отразившегося импульсов.

На рис. 5 видно, что формы отразившегося и падающего импульсов различны, что согласуется с экспериментальными результатами, представлен- ными в работе [16]. Стоит отметить и значительное (практически в два раза) уширение отражённого импульса по сравнению с падающим.

Заключение

Получены следующие результаты:

• 1.    Для общей постановки краевой задачи для волнового уравнения получено аналитическое решение в виде ряда (10).

• 2.    Построена и численно исследована явная схема для краевой задачи (11). Скорость сходимости схемы близка к квадратичной.

• 3.    В частном случае получено совпадение между численным и аналитическим решением.

• 4.    Показано, что разностное решение волнового уравнения на порядок точнее, чем разностное решение уравнений Максвелла FDTD-методом с помощью программы Fullwave при одних и тех же параметрах сетки (СКО 0,014% и 1%).

• 5.    Произведено сравнение теоретических и расчётных коэффициентов отражения и пропускания для ультракороткого импульса света длиной 4,223 фс при прохождении через стеклянную пластину; СКО составила 0,47%.

• 6.    Численно показано, что при полном внутреннем отражении ультракороткого импульса (1 фс) от раздела двух сред даже без учёта дисперсии материала происходит искажение и уширение импульса.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), гранта Президента РФ поддержки ведущих научных школ (НШ-4128.2012.2) и гранта РФФИ (12-07-00269).