Моделирование распространения звука в жидкости с пузырьками воздуха

Исследование распространения звука в жидкостях с газовыми включениями (пузырьками) является актуальной задачей акустики, имеющей широкий спектр приложений — от гидроакустики до биомедицины. Присутствие газовых включений существенно модифицирует акустические свойства среды, приводя к дис- персии, поглощению и нелинейным эффектам. В случае дисперсии наблюдается зависимость фазовой скорости звука от частоты, обусловленная резонансными колебаниями пузырьков. Резонансная частота пузырька определяется его радиусом и свойствами окружающей жидкости. Также энергия звуковой волны поглощается за счет вязкого трения в жидкости, теплообмена между пузырьком и жидкостью. При высоких интенсивностях звукового поля наблюдаются нелинейные эффекты, связанные с колебаниями пузырьков, такие как генерация высших гармоник, образование ударных волн и кавитация [1, 2, 3].

В настоящем исследовании предложена графическая визуализация процесса распространения акустических волн в жидкостях, содержащих газовые пузырьки. Для численного анализа использовалась модель, реализованная в среде COMSOL Multiphysics, которая демонстрирует высокую эффективность при решении широкого круга акустических задач. Это подтверждается многочисленными исследованиями, включая моделирование параметров резонатора Гельмгольца на основе уравнений Навье-Стокса, анализ проникновения звуковых волн в среды с различными коэффициентами поглощения, а также расчет полного акустического давления и его пространственного распределения для модели акустического датчика. Применение данного инструмента позволяет получить детальные результаты, значимые для дальнейших исследований в области акустики и гидродинамики [4, 5].

Описание модели исследования

Моделирование распространения акустических волн проведено для жидкостного резервуара, аппроксимируемого параллелепипедом размером 0.1×0.1×0.5 м. На границах резервуара задано условие жесткости, что предполагает полное отражение звуковых волн без диссипативных потерь. В качестве рабочей среды использована вода при стандартных термодинамических параметрах P=1 атм и T=293.15 K. Акустическое возбуждение осуществляется двумя источниками, расположенными на левой боковой грани резервуара. Для учета влияния газовых включений принято приближение несжимаемости среды.

Численный анализ выполнен с использованием программного комплекса COMSOL Multiphysics, реализующего расчет на основе уравнения Гельмгольца:

^

V-("V ? -a)—^P t ) = Q m ,

P t = Р + P b , ы к& = (тт)². ^ с

Результаты исследования модели с пузырьком воздуха диаметром 0,09 м

Для данной модели средствами программного комплекса COMSOL Multiphysics построена вычислительная сетка, используемая для моделирования распространения звуковых волн (рис. 1).

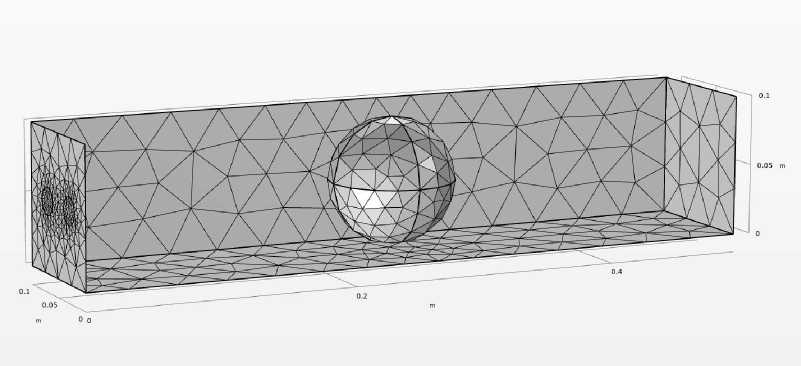
Рис. 1. Сет ка дл я р асч е т а р а спр е д е л ени я акус тического давления в системе

В чи с ле нном мод е ли р овании сетка играет ключевую роль, опреде ля я т очн ос ть и эф ф е к ти вност ь рас че т ов. Она представляет собой разбиение расче т н ой обла с ти на эле ме нт ы кон ечн ог о объема или конечных элементов, внутри кот оры х чи сленно р е ша ютс я у рав н е ни я а ку ст и к и .

М акс им а л ьны й раз м е р элеме н т а у ст ановле н к а к λ/5, где λ — максимальная дли н а а ку ст и чес кой вол ны в среде. Этот параметр выбирается исход я и з тре б о в а н ий к д и ск р ет изаци и волновых процессов, обеспечивая адекватное ра зре ш ени е звуковых волн . М и н и мальный размер элемента в два раза меньше макси м а льн о г о. Это повы шае т т очность расчетов в областях с высокой градиент н ост ью аку с т и чес ког о поля , н а п ример, вблизи границ объектов и пузырька. Сделан о также з агу щен ие с ет к и в обл ас т и и ст очн и к а з вук а, что позволяет точно моделировать проце с с ы г е не р аци и и распространения волн. Как правило, вблизи ист оч ник а наблюд а ются резк и е и з менения акустического давления, требующи е б о ле е д ет ализированной сетки.

Созда н ная се тк а и сп ользует ся для чи слен но го ре шения у равнения Гельмголь ца, оп и сы в а ющег о рас пространение звука в рассматриваемой систе ме . К аче ст в е н ное п ост р оен ие се тки позволяет минимизировать численные ошиб к и , и зб е жа т ь д и с перс ион н ых и скажений волнового фронта, а также повысить схо д им ост ь ме т ода к онечн ых элементов.

На рисунке 2 пред ст авлено распределение полного акустическог о д ав л ения в ра с че т н ой о б ла с т и п ри частоте 8333,3 Гц, соответствующей длине во лн ы , р а в ной дву м ди а ме т рам п у з ырька. Данный расчет выполнен на основе ранее п ре дст а в л ен ной в ычи с лит е льн ой с е т к и , обеспечивающей достаточное разрешение волновых процессов.

В ЕСТН ИК БУРЯ ТСКО Г О Г ОСУДАР СТ В ЕНН ОГ О УНИВЕ РСИ ТЕ Т А .

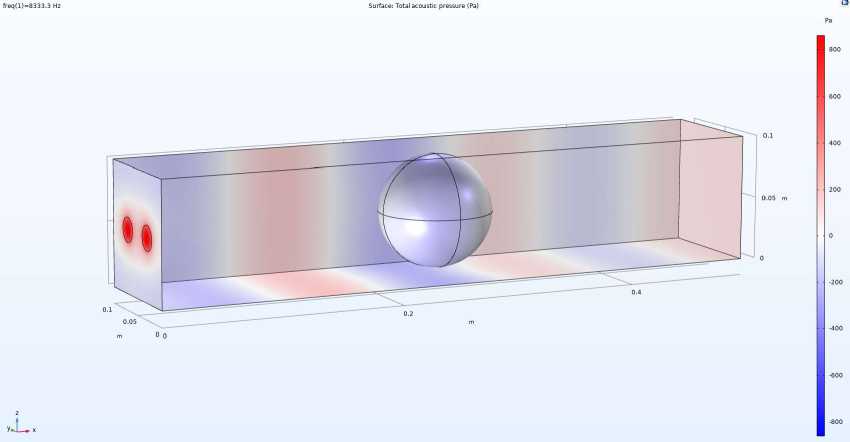
Рис. 2. Ра с п р е дел е н ие акус ти че ского д а вл ен и я пр и ч а с т оте, с оо тв ет ств у ющ е й д лине волны, равной двум диаметрам пузыря (833 3,3 Гц )

В да нно й мод ел и на б л юдае тся о гибание пузырька звуковой волной. Пузырек о к азыва е т срав нит е л ьно небольшое влияние на распространение ак устич еск о й во лны. Это о бъ я сн яет с я тем, что длина волны значительно превы шае т р а зме р препя тстви я , ч то п р иводит к проявлению эффекта дифракции и слабо му р а сс е я нию во лны н а пузы р ь к е. Осн о вн ой фронт акустической волны остается практи ч е ск и неи з м енн ы м за п узырьком, что указывает на слабую акустич еск ую же с т к о сть пузыр ьк а при данн ой ч а сто т е во зб уж дения .

На бл юд ает ся н а л ич и е л ок ал ьн ы х во змущ е ний вб л изи пузыр ьк а. Несмотря на о б щ и й хар ак т ер о гиб а ни я, вблизи пузырька наблюдаются небольшие локальные ва р иац ии акус тич ес ко г о давления. Это связано с взаимодействие м падающ е й во лны с грани цей г а зо в ого включения и образованием зон слабого ак ус ти ч е ск о го к о нт р а ст а. Э ти в о змущ е ния ук азыва ю т на в оз мож но е фо р м ир о вание слабых рас се янных во л н , о д на к о и х амплитуда недостаточна для существенного изм ен е ния о б щ ей карти н ы р а сп ро ст ране ния зву ка.

Также в данной мо дели наблюдаются стоячие волны и интерфере нция . В пре дела х расч ет н ой области наб л юдае т ся х а ра ктер ная инт ерф ерен ционная картина с ч е р е дую щи мис я зо нами положительного и отрицательного акустиче ско г о д а в ле ния . Четк ие п о л ос ы да вления свидетельствуют о формировании ст ояч их во лн ме жду с т е нк ам и со с уда , что ожидаемо для замкнутых акустических си стем с жесткими границами.

Резу л ь таты мо д ел ир ования демонстрируют, что при данной д л ине в о лны вл и я ние пу зыр ьк а на акустическое поле минимально, а доминирую щим ф акт о р о м в си сте ме о с таетс я интерференция волн, обусловленная отражени я ми о т ж е стк их стено к со су да. В дал ьней ш ем ан ал и зе р а сс мотрено поведение системы при ч а сто те, ср авн имо й с резонансной частотой пузырька, где ожидаютс я б о лее в ы р аж енные э фф ек т ы р ассея н и я и пог л о щ е ния зву ка .

Н а р ис унке 3 пре дставлено распределение полного акустического д а вл е ния пр и ч асто т е 1 6 6 67 Г ц, ч то со о тв е тс твует длине волны, равной диаметру пузырь ка. Данны й с л уча й пр и н цип иал ьн о о т л ич ает ся о т пр еды д у щ ег о ( рис. 2), так как со о тно шени е р азмер о в пузырька и длины волны приближается к резо нан сны м условиям рассеяния.

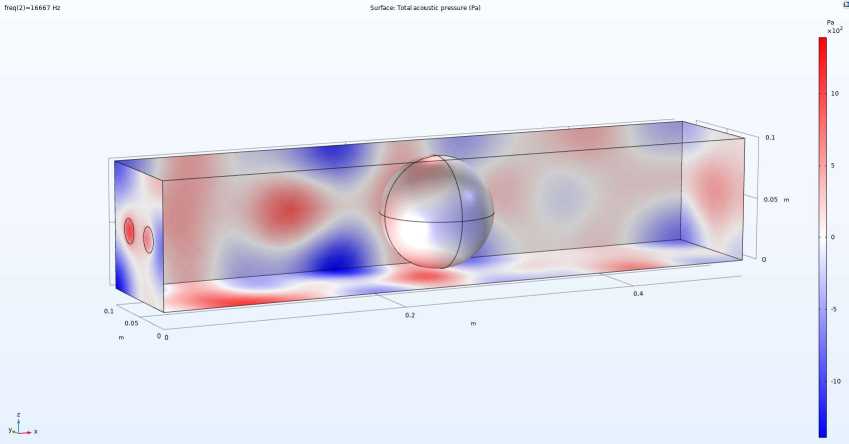
Рис. 3. Р а с п ре дел ени е ак ус ти ч е ско го д авлен и я п ри частоте, соо тве тству юще й длине волны, равной целому диаметру пузыря (16 6 6 7 Г ц )

В моделируемой сист еме наблюдаются такие физические эффект ы, как усиле ние р ас сеян ия на пузыр ь к е. В отличие от случая с большей длиной волны (рис. 2) здесь наб л ю д ается выр а ж енное взаимодействие звуковой волны с пузырьком. В о к руг пузы р ька фо р мируются отчетливые зоны повышенного и по н и жен но г о давления, что указы в ае т на значительный вклад пузырька в проце сс р ассе я ния ак уст ич еско й в о л ны. Э то подтверждает известные теоретические результаты, со гл ас но кото рым расс еяние звука на сферических включениях на ибо л ее в ыра жено , ко г д а д л ина во лн ы ср авнима с раз ме р о м рассе ив ат ел я .

В сист е ме так же формируются сложные интерференционные карт ин ы . В рас ч етно й о бласти видн а сло ж ная стр укт ур а че р е д у ю щихся зон положительного и о тр и цат е л ь ног о акусти ч еского давления, что свидетельствует о разв итии интер ф е р енцио нн ы х пр о цес сов. Пузырек не только рассеивает падающую в о л н у, но и взаимо дейст ву ет с о тр а женными волнами, что приводит к возникнов е ни ю сл ожных стоячих вол н в нутри ограниченного объема. Это согласуется с эк спериме н тал ь ны ми набл ю д е ниям и акустических резонансных явлений в жид к и х сре д ах с включениями.

Кроме того, наблюдается локальное усиление акустического давления. Вблизи пузырька заметны области локального увеличения амплитуды акустического давления. Данный эффект может быть связан с образованием частичных стоячих волн вблизи границы пузырька, что типично для акустических резонаторов. При дальнейшем увеличении частоты можно ожидать усиления подобных эффектов вплоть до нелинейных явлений в среде.

Таким образом, результаты моделирования при частоте 16667 Гц показывают значительное влияние пузырька на распространение акустической волны, включая выраженное рассеяние, локальное усиление давления и сложные интерференционные эффекты. В дальнейшем анализе целесообразно исследовать поведение системы при еще более высоких частотах, близких к резонансной частоте пузырька, а также рассмотреть вклад возможных нелинейных эффектов при интенсивных звуковых полях.

Заключение

Исследование подтвердило, что программный комплекс COMSOL Multiphisics является мощным инструментом для моделирования акустических процессов в жидкостях с газовыми включениями. Его использование позволило визуализировать распространение звуковых волн с высокой детализацией, а численный анализ продемонстрировал точность и надежность расчетов. Гибкость метода конечных элементов, реализованного в программном продукте, делает его эффективным средством для исследования сложных акустических явлений, таких как рассеяние, интерференция и взаимодействие волн с пузырьками.

Дальнейшие исследования будут направлены на анализ поведения системы при более высоких частотах, включая ультразвуковой диапазон, где ожидается усиление нелинейных эффектов. Особый интерес представляет влияние интенсивных звуковых полей на формирование кавитации и других резонансных явлений, что может иметь практическое значение для различных технологических и биомедицинских применений. Расширение модели на системы с множественными пузырьками позволит глубже понять механизмы взаимодействия звуковых волн с неоднородной средой и открыть новые возможности для управления акустическими свойствами жидких сред.