Моделирование реологических свойств жаропрочных материалов в условиях высокоскоростной обработки резанием

режимов резания, необходимых для моделирования реологии материала при ВСО.

Эксперименты по измерению силы резания проводились с помощью 3-х осевого динамометрического стола Kistler9257B с регистрацией изменения составляющих усилия резания F_x,F_y,F_z в реальном времени. Обработку образцов производили концевой цилиндрической фрезой диаметром 12мм на обрабатывающем центре MikronUCP800 Duro. Технологические параметры обработки: боковой съем 5 = 0,1 мм, съем по высоте t = 4 мм, подача на оборот фрезы f _o6 = 0,32 мм/об, фрезерование попутное, обработка с СОЖ.

ВСО с точки зрения сопротивления пластическому деформированию характеризуется одновременным действием процессов вязкого упрочнения (вязкотекучесть) и температурного разупрочнения. В виду того, что измерение температуры резания в процессе фрезерования у вершины радиуса инструмента технически затруднительно по причине локализации области интенсивного деформирования в диапазоне 0,01…0,2мм и перемещении очага пластической деформации (ОПД) со скоростью до 800 м/мин, результат измерения имеет большую погрешность и носит оценочный характер. Поэтому для оценки температуры резания целесообразно воспользоваться аналитическим методом, изложенным в работах [3, 4].

Значения температуры 0 в зоне резания оценивается по теоретическим зависимостям, которые получены при рассмотрении теплового потока от квазистационарного быстродвижу-щегося полосового источника тепла постоянной интенсивности, расположенного под углом Р в условной плоскости сдвига. Тепловые источники при резании имеют объемный характер, так как пластические деформации металла протекают в определенных объемах зоны резания [2, 3].

Между значениями температуры резания 6 и температурой 6 A в условной плоскости сдвига существует связь, которую оценочно можно определить из теоретической зависимости [4]:

6 в л

1,32 Pe^0-375B^0,665E ^0,055 [ cos у + sin у - B ( cos у - sin у ) [' 275

F ^,15 D ⁰⁰⁴⁵ erf ^0,6 ^ PeB sin ⁰ , ⁰³ а ( cos у + B sin у )

, (1)

где F,D,Е– безразмерные комплексы (критерии подобия), определяющиеся выражениями:

X

F = —— p - критерий, отражающий влияние X геометрии инструмента и отношения теплопроводностей инструментального Xp и обрабатываемого X материалов, р = у-(а + у) -

угол заострения режуще-

го клина, рад; а , у - соответственно задний и передний углы.

s

D =--критерий, характеризующий геомет- рию сечения среза;

E = — - критерий, характеризующий отно

• сительную величину радиуса закругления инструмента r_и ;

При B>0,4 получаем выражение для температуры резания [4]

0,95 0 s ₀ Pe ⁰³⁷⁵ E  5

^в n^on 43C_ppB⁰⁶²⁵F^0,5D ^0,045 (1 - sin у )⁰⁶⁵ sin^0,03 а ’ ⁽²⁾

где n_оп –поправочный коэффициент, учитывающий реальные условия резания.

Для случая B > 0,4 соответствующего рациональным режимам резания получена более про- стая теоретическая формула степенного вида [4]

B _      mPen

F^kD^p ( 1 - sin у ) q ,             ⁽³⁾

в которой коэффициент m и показатели степени n, k, p и q .В зависимости от условий выполнения процессов резания должны определяться по табл. 1 [4].

График зависимости расчетной температуры резания от скорости резания представлен на рис. 1 (б).

Для моделирования силового режима резания в общем виде целесообразно использовать о 6 - в относительные параметры 6 =-----0--отно-

6 max - 6 0

сительная температура резания; v =-----—— v - v max min

F рез

• - относительная скорость резания; p =-- ° . 0 st

относительное удельное усилие резания, где O s ₀ - предел текучести обрабатываемого материала при базовой температуре (в нашем случае O s ₀ = 600МПа при 6 =50 0⁰С [5]). Учитывая изложенное, рассматриваемая модель примет вид: p = ^ ( v ^{, 0} )| f z = со_п51 ,           (4)

где ^ ( v , 6 ) - функционал, зависящий от реологических свойств материала и геометрии режущей части инструмента.

В данной работе используется феноменологический подход к реологическим свойствам обрабатываемого материала, поэтому для конструирования принципиальной схемы модели воспользуемся корреляционным анализом экспериментальных данных. Гр а фики взаимных корреляций параметров p , v , 6 представлены на рис. 2

Таблица 1. Значения коэффициентов для определения угла относительной плоскости сдвига [4]

Pe	FD 0,3 (1 - sin у )0,25	FD 0,3	m	n	k	p	q
	Pe	Pe ( 1 - sin у ) 0,4
Pe >  120	< 0,03	< 0,05	0,80	-0,14	-0,03	-0,01	0,95
	< 0,45	< 0,665	0,56	-0,06	0,09	0,03	1,00
		>0,665	0,35	0,36	0,56	0,16	1,20
	> 0,45	< 0,665	0,51	0,02	0,23	0,07	1,04
		>0,665	0,30	0,47	0,76	0,23	1,25

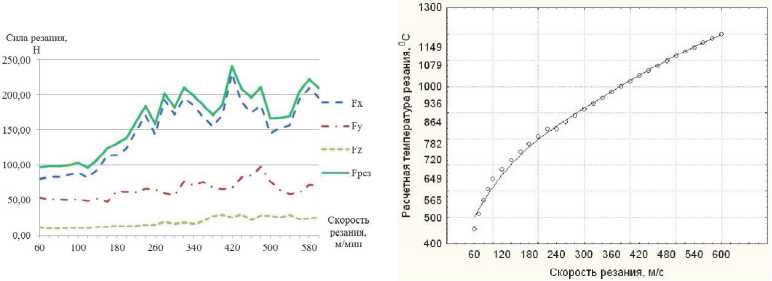
Рис. 1. Зависимость составляющих и результирующей силы резания F и расчетной температуры резания 6 от скорости резания при высокоскоростном фрезеровании образца из ХН45МВТЮБР-ИД (ЭП718 ИД):

подача 0,32 мм на оборот, фреза диаметром 12 мм, боковой съем 0,1 мм, съем по высоте 4 мм

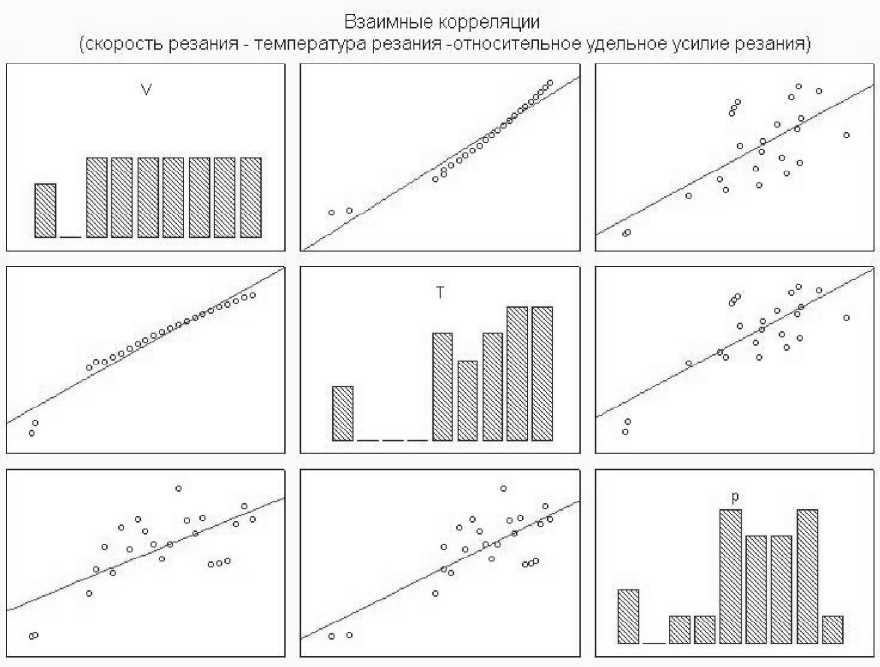
Рис. 2. Корреляция параметров скорость резания V – расчетная температура резания и T - относительное удельное усилие резания P при высокоскоростном фрезеровании образца из ХН45МВТЮБР-ИД

Анализ корреляционных зависимостей показывает, что скорость резания и вызываемая диссипацией мощности пластической деформации температура резания оказывают совместное мультипликативное воздействие на удельное усилие резания, поскольку ни один из параметров взятых отдельно не показывает сильную корреляционную связь с силой резания. С другой стороны между температурой и скоростью резания существует связь, с коэффициентом корреляции близким к 1, что обуславливается условиями проведения эксперимента и принятой функционально-определенной зависимостью между этими параметрами. Принимая во внимание изложен- ное, реологические свойства обрабатываемого материала можно представить в виде принципиальной схемы, изображенной на рис. 3, объясняющей феноменологию процесса резания.

Вязкопластические свойства в зависимости от относительной скорости резания v описываются функционалом f 1 ( v ) , температурное разупрочнение - функционалом f 2 ( 6 ) . Коэффициент а ₀ интегрировано отвечает за жестко-пластические свойства и за деформационное упрочнение. В данной модели, поскольку { 5 , t, f z } — const для рассмотренных условий эксперимента, деформационное упрочнение как функция технологических параметров не учитывается.

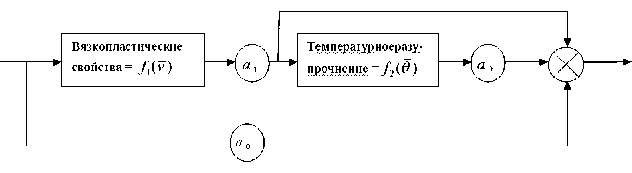
Рис. 3. Принципиальная схема реологических свойств вязкопластического материала, обрабатываемого высокоскоростным резанием

Коэффициент a 1 характеризует степень влияния вязкопластического упрочнения, а коэффициент a ₂ - температурного разупрочнения. В общем случае значения коэффициентов являются функциями геометрии режущего инструмента, технологических параметров { 5 , t , f_z } , которые определяют размеры и форму ОПД и свойств сопротивления обрабатываемого материала динамической нагрузке при резании. Вектор коэффициентов

'a0 = а0к(fZ,5,t,а,у,....)

a1 = k(fz,5,t,а,у,....)

v a 2 = ^5в(Л \, Cp, P)    v получают по результатам обработки экспериментов, причем значение коэффициента k(fz ,5,t,а, у,....) , учитывающего размеры и форму ОПД, можно оценить аналитически [9].

Вид функциональных зависимостей f 1 ( v ) и f , ( в ) можно задать, используя подходы, применяемые в механике сплошных сред, которые устанавливают определяющие соотношения между напряженным и деформированным состоянием в условиях динамического нагружения. Наиболее простой и часто применяемой моделью является эмпирическая модель Джонсона-Кука. Эмпирическая модель Джонсона-Кука [6, 7] определяет следующее соотношения для поля напряжений ( о y )

G y i , i p , в ) = ( a + b • (E_p ) n )( 1 + c • ln( J , ) )( 1 - T m ) , (5) где i _p -эквивалентная пластическая деформация, E _p - эквивалентная скорость деформации, a , b , c , n , m - константы, зависимые от материала. Приведенные скорости деформации Ё _р и температура _T , задаются зависимостями

- Ё - Т-Т

р =    ■ Т = -__IO- i               ; T                       ,

p р 0            пл 0

где Ё _р 0 - интенсивность скорости пластической деформации, полученная в квазистатических испытаниях, проводимых с целью получения значения предела текучести и параметров упрочнения a , b, n ; T₀ - некоторая постоянная температура; T_m - температура плавления. Для т <  0 предполагается m=1.

Сравнивая представленную на рис. 3 принципиальную схему реологических свойств обрабатываемого материала и феноменологическую модель определяющих соотношений Джонсона-Кука, можно предложить следующий вид зависимостей для функционалов f 1 ( v ) и f ) ( v ) : Л ⁽ v ) = ^ln ( v ) , f > ^{( в} ) = ^e m . В этом случае модель реологических свойств вязкопластического материала, обрабатываемого резанием примет вид:

р = a ₀ + a 1

ln

v - v .

min

v - v • max min /

1 + a 2

вв. в-в

0 пл

a 3

Неизвестные коэффициенты, входящие в модель (8) для высокоскоростного фрезерования жаропрочного хромисто-никелевого сплава ХН45МВТЮБР-ИД рассчитывались методом нелинейного регрессионного анализа по экспериментальным и расчетным данным, приведенным на рис. 1. Расчет производился комбинированным методом Розенбрука - квази-Ньютона. Вектор начального приближения коэффициентов – (0,0,0,1). В качестве функции потерь была выбрана квадрат разности значений эксперимент-модель. Расчетные значения коэффициентов, входящих в модель (6) для сплава ХН45МВТЮБР-ИД определены зависимостью (7).

p = 0,85 + 0,061ln | v -^° || 1 - 1,347 1 ^{в 2000} ||

I 560 JI         I 1543 Ji .⁽⁷⁾

Достоверность модели (7) составляет 66,3%, что является высокой величиной, несмотря на разброс экспериментальных значений усилий резания относительного номинального значения, вызванного вибрациями фрезы по резонансным частотам. Распределение среднеквадратичных отклонений рассчитанных по модели (7) и наблюдаемых значений представлено на рис. 4. На рис. 5 представлен 3-х мерный график модели (7) и экспериментально полученные значения относительных усилий резания для сплава ХН45МВТЮБР-ИД.

Анализируя данные, представленные на рис.4, можно сделать следующие выводы.

1. Наиболее интенсивный рост вязкопластических свойств (скоростного упрочнения) обраба-

тываемого материала наблюдается в диапазоне скоростей резания 40-200м/мин. Вязкопластические свойства явно подчиняются логарифмическому закону, что хорошо объясняется механизмами дислокационной теории сопротивления пластическому деформированию. Наличие интерметал-лидных включений искажает матрицу сложнолегированного многофазного сплава, что препятствует движению дислокаций, ответственных за пластическую деформацию.

Модель: p=a0+a14og((v-40y560)41+a24(T-2000y(1543))‘‘a3

р=0.85+0^61Чод((хЛ)у560)Ч1НД47Ч(у-2000У(15^

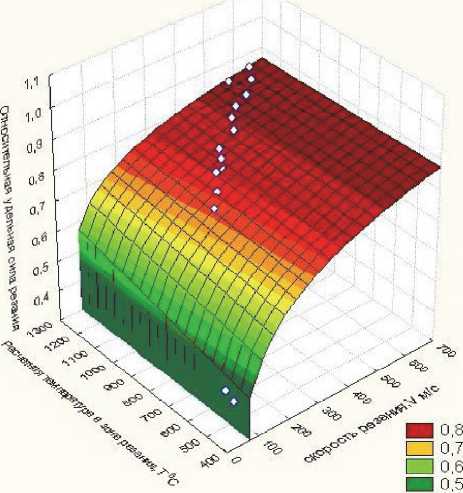
Рис. 4. Модель реологических свойств (реологическая поверхность) и экспериментальные данные (относительное усилие - скорость резания – температура резания) при высокоскоростном фрезеровании образцов из хромисто-никелевого сплава

ХН45МВТЮБР-ИД

• 2.    В диапазоне скоростей резания 50-350 м/ мин повышенная температура в зоне резания способствует увеличению вязкопластического упрочнения. Об этом свидетельствует увеличение наклона касательных к изотермическим сечениям реологической поверхности (рис. 4) с ростом температуры. Интенсивное охлаждение за счет подачи СОЖ в зону резания в этом скоростном диапазоне позволяет существенно снизить усилия резания. Этот вывод хорошо согласуется с практикой фрезерования сплава ХН45МВТЮБР-ИД.

• 3.    В диапазоне скоростей резания от 400м/мин и выше наблюдается температурное разупрочнение обрабатываемого материала (соответствующий температурный диапазон обработки без подачи СОЖ - 1000 ^оС и выше.). Температурное разупрочнение невелико и не компенсирует рост вязкопластического упрочнения.

• 4.    Анализ экспериментальных данных по соотношению силы и скорости резания показывает, что в диапазоне скоростей резания 450..580м/мин, что соответствует температурному интерва-лу1050…1200 ^оС, наблюдается локальное снижение усилия резания. Этот феномен локального снижения усилия резания при высокоскоростном фрезеровании в области высоких температур носит название “кривой Соломона” [1]. Для объяснения причины этого явления следует обратиться к квазибинарной диаграмме состояния Ni-Cr. Из диаграммы [8] следует, что температура 1180 ^оС является температурой эвтектойдно-го превращения для сплавов с содержанием Ni 35-62% по массе. Поэтому сплав, находящийся в температурной области близкой к рассмотренной, претерпевает полиморфное а + у □ Р + у превращение. Такое метастабильное состояние является причиной локального снижения усилия резания за счет дополнительной энергии, кото-

  

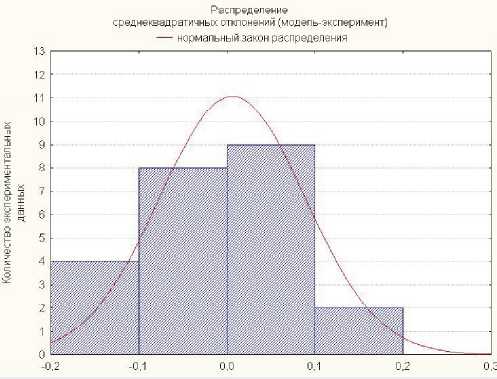
  Рис. 5. Распределение среднеквадратичных отклонений модель-эксперимент при ВСО сплава ХН45МВТЮБР

  
  

• 5.    Для моделирования реологических свойств материала, подвергнутого механической обработке в температурной области полиморфного превращения и соответствующей этой области “кривой Соломона” по усилиям резания, целесообразно использовать несколько кусочно-нелинейных аппроксимирующих зависимостей вида (6). В этом случае в качестве реперных значений скоростей и температур из (6) будут применимы следующие величины: v = { v », , V _M, v ’J) = МДМ = {W_MA} , где индекс min относится к минимальной скорости резания, индексы 01,02,03 – к значениям на входе, в точке локального минимумапо усилиям и на выходе из области полиморфных превращений. Постоянные коэффициенты, входящие в зависимость (6) будут определяться матрицей a_ij , где i = (0,1,2,3), j = (01,02,03) .

рая выделяется на пластическую деформации при смене типа кристаллической решетки. В целом, снижение усилия составляет не более 20% от достигнутого максимального значения, поэтому фрезерование в данном температурном диапазоне не может рассматриваться в качестве рекомендованных технологических режимов.

Подводя итог материалам, изложенным в данной статье, можно сделать выводы:

Предложенная авторами феноменологическая модель вязко-пластичного материала достоверно отражает его реологию при высокоскоростном фрезеровании.

Полученное локальное снижение усилия резания в области полиморфных превращений при обработке фрезерованием сплава ХН45МВТЮБР-ИД незначительно, поскольку требует использова- ния специального режущего инструмента с оптимизированной под эти режимы геометрией и проведения дальнейших исследований.