Моделирование режимов генерации оптического излучения в полупроводниковом волноводе с распределённой обратной связью, создаваемой волной пространственного заряда

Волны пространственного заряда (ВПЗ) представляют собой пространственно-временные возмущения зарядовой плотности, возникающие в полупроводниках с отрицательной дифференциальной подвижностью в сильных электрических полях [1 –3]. ВПЗ могут усиливаться и распространяться со скоростью, близкой к скорости дрейфа носителей, что позволяет использовать их при создании тонкоплёночных усилителей бегущей волны и активных линий передачи, реализуемых в полупроводниковых плёнках [3, 4]. В работе [5] показано, что в пьезополупроводниках ВПЗ генерируются звуковыми волнами и могут оказывать существенное влияние на дифракцию света. При этом дифракционная эффективность ВПЗ-опти-ческого взаимодействия возрастает пропорционально квадрату длины волны света при приближении его частоты к плазменной частоте, и поэтому наиболее существенна в среднем и дальнем ИК-диапазоне, а также в терагерцовой области [6]. Формирование такой электронной решётки можно осуществить также и для полупроводниковых структур на основе n-GaAs или n-InSb в преддоменном режиме в условиях эффекта Ганна.

Физической основой ВПЗ-оптического взаимодействия является отклонение концентрации свободных носителей заряда от равновесной, возникающее при распространении ВПЗ в кристалле. Это приводит к периодическому изменению диэлектрической проницаемости (ДП) с глубиной модуляции, достаточной для эффективного ВПЗ-оптического взаимодействия. В результате междолинного переноса электронов дифференциальная проводимость образца становится отрицательной, что создаёт условия для генерации и усиления собственных ВПЗ [7]. Теория ВПЗ и эффективный метод их возбуждения, основанный на освещении кристалла бегущей интерференционной картиной, рассматривался в статье [8]. В работах [9, 10] рассмотрена дифракция света на ВПЗ в объёмных кристаллах полупроводника. В цикле работ [11 – 15] проведён анализ дисперсионных свойств ВПЗ в полупроводниковом волноводе и показана возможность эффективного коллинеарного взаимодействия оптических волноводных мод с бегущими и усиливающимися по амплитуде ВПЗ при различных граничных условиях.

В отличие от работ [12– 14], где рассмотрена усиливающаяся по амплитуде ВПЗ, в данной статье рассматривается ВПЗ, бегущая по n-GaAs-волноводу без усиления и поглощения, а режимы усиления и генерации оптических волн TE-типа исследуются для случая внешней оптической накачки. ВПЗ образует периодическую решётку и обеспечивает получение распределённой обратной связи для прямой и обратной волн. Анализируются условия фазового рассогласования и накачки, обеспечивающие получение в структуре генерации оптических прямой и обратной (холостой) волн без концевых отражателей.

Постановка задачи и основные соотношения

Рассмотрим оптический волновод, состоящий из подложки (среда 1), полупроводниковой плёнки (среда 2) толщиной t WG и покровной среды (среда 3) с ДП ε j = n j 2 ( j = 1, 2, 3). Пусть ось x перпендикулярна границам раздела сред, к структуре вдоль оси z приложено постоянное электрическое поле E 0 , при этом в качестве электродов могут использоваться прозрачные материалы, например, InGaBiAs: Si [16] (см. рис.1).

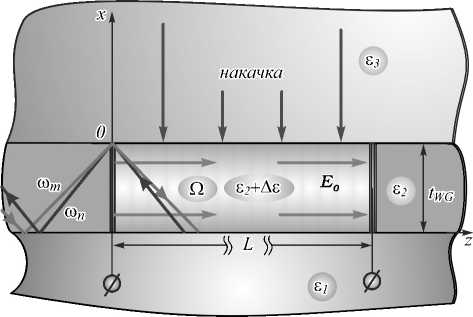
Рис. 1. Геометрия структуры. Взаимодействие прямой и обратной оптических волн и ВПЗ с соответствующими частотами ω m , ω n и Ω

Задачу условно можно разделить на 2 части: «твёрдотельную», связанную с описанием ВПЗ, и «оптическую», связанную со взаимодействием оптических TE-мод. Известно, что для реализации режима генерации ВПЗ в полупроводниковом слое необходимо выполнение условия Крёмера [1], которое для GaAs имеет вид 1010 ≤ n0 L ≤ 1012 см-2, где n0 – концентрация равновесных носителей, L – длина области взаимодействия [17, 18]. Подбирая уровень легирования волноводного слоя, его длину и толщину, а также значение прило- женного поля E 0, которое в n-GaAs должно превышать пороговое Et ≈ 3 кВ/см, можно добиться возникновения электронной решётки, образованной ВПЗ (без перехода в доменный режим Ганна) [3,9].

Основными уравнениями, определяющими волновые возмущения потока электронов в полупроводнике, являются уравнение непрерывности, Пуассона и полного тока. Используя квазистатическое приближение (rot E 1 =0), а также электродинамические граничные условия, можно получить дисперсионное уравнение, связывающее параметры полупроводникового слоя с частотой Ω и константой распространения Q ВПЗ (см., например, [3, 11])

DQ 2 + i ( Ω- Qv 0 ) + µ d ω m = 0 , (1)

где µ d = µ 0 ^{- 1} (d v /d E ) – отрицательная (приведённая) дифференциальная подвижность, µ 0 – подвижность «неразогретых» электронов, ω m =4 π en 0 µ 0 / ε 2 – частота максвелловской релаксации, соответствующая времени потери электронейтральности полупроводника, e – заряд электрона, n 0 – равновесная концентрация носителей, ν 0 – скорость «горячих» носителей. Два решения уравнения (1) соответствуют прямой (сносо-вой) и обратной (диффузионной) ВПЗ. Поскольку обратная волна быстро затухает [2], далее мы рассматриваем только прямую ВПЗ, бегущую вдоль оси z без усиления, которая создаёт возмущение ДП и возбуждается с помощью прозрачных электродов.

Как видно из уравнения (1), ВПЗ распространяется без поглощения (или усиления) на частоте

Ω= v 0 Q = v 0 J -µ d ω m / D , (2)

где D – коэффициент диффузии. При этом координатная зависимость ВПЗ-возмущения ДП в слое полупроводника может быть представлена функцией:

Δε ( x , z ) = Δε ( x )cos( Ω t - Qz ). (3)

Как показано в работах [9,11], глубина модуляции ДП в волноводной плёнке

Δε ( x ) = Δε ≈ e ε E 1 Q / m * ω 2 , (4)

где E 1 – амплитуда возмущающего электрического поля в полупроводнике в преддоменном режиме, m ^* – эффективная масса электрона, ω – частота света. Численные оценки величины Δε для кристалла (n-GaAs) на длине оптической волны λ = 10,6 мкм при m ^* ≈ 0,063 m 0 ( T =300 К), где m 0 – масса свободных электронов, ε 2 ≈ 12, E 1 ≈ 300 В/см ( E 1 <<  E 0 ) дают значения Δε ≈ 10 -5 . При достаточно высоком уровне усиления это позволяет осуществить генерацию, что будет показано ниже.

Для оптических TE-мод ( H x , E y , H z ) рассматриваемого волновода электрическое поле в поперечном направлении (профильная функция) даётся выражением [19]

exp( - qx ),

x >  0,

E ym ⁽ x )    C m ' ^-

[cos hx - q sin hx ], - t_WG h

[cos ht_wG+ q sin ht_wG ] x h

< x < 0,

Удобно представить амплитуды оптических волн следующим образом:

A ( z ) = A' ( z ) exp( Y z ), B ( z ) = B' ( z ) exp(— Y z ).

Решения уравнений (9) выражаются следующим образом:

x exp[ p ( x + t WG )], x <- t WG .

Здесь поперечные компоненты волнового вектора в каждом из трёх слоёв p ² = p m - k ₀ ² 8 1 , h ² = k ₀ ² 8 2 - P m , q ² = P m - k 02 8 3 волновое число k ₀ = to / c , c - скорость света. Постоянная C m определяется из условия нормировки мощности моды порядка m в структуре:

A ' ( z ) exp[( - i AP + y ) z ] = B (0) x

( Y - i Ap ) sinh[ S ( L - z )] - S cosh[( S ( L - z )] ^X       ( y- i Ap )sinh( SL ) - S cosh( SL )

B ( z ) exp[( i AP - y ) z ] =

= _B (0)       i к mm sinh[( S ( L - z )]

( Y - i Ap ) sinh ( SL ) - S cosh( SL )^.

n        to emca^ J[Eym (x)] 2dx = P , 8nk0 X L

где a y = 1 см – длина вдоль оси y , соответствующая единичной мощности, переносимой модой ( P 0 = 1 эрг/с). Дисперсионное уравнение для TE-мод трёхслойного невозмущённого волновода в общем случае имеет вид (см., например, [20,21]):

ht_WG - n m - arctan ( q / h ) + arctan ( p / h ) = 0 . (7)

Здесь введён вспомогательный параметр S = ^ | к _mm | ² + ( y- i AP ) ² . Решения (10) позволяют получить энергетические коэффициенты отражения и прохождения мод в волноводе с областью взаимодействия длиной L :

R =

E r (0) E i (0)

B ' (0)

A (0)

к _mm sinh SL

Отметим, что константа распространения определяет эффективный показатель преломления m -й волноводной моды: n_m = P _m / k ₀.

Для получения усиления прямая оптическая волна может быть введена в волновод (вне области взаимодействия L ) с помощью призменного или решёточного элементов связи, позволяющих селективно возбуждать m -ю волноводную моду за счёт изменения угла падения лазерного пучка. Аналогично можно осуществить вывод из структуры обратной волны (усиливаемой либо генерируемой). Частоты прямой, обратной оптических волн и ВПЗ, движущихся вдоль оси z , связаны соотношением to _m = to _n + Q . Используя теорию связанных мод (например, [19]), можно записать коэффициент связи для волноводных ТЕ-мод с одинаковыми индексами ( m = n ):

( Y- i Ap )sinh( SL ) - S cosh( SL ) ’

T =	2 E i ( L )		2 A ' ( L )
	E i (0)		A (0)

S

( y - i Ap ) sinh ( SL ) - S cosh( SL )

Отметим, что эти соотношения соответствуют коэффициентам отражения и прохождения волн в волноводном лазере с гофрировкой [19,22]. За счёт накачки в волноводной плёнке отрезок волновода играет роль усилителя для отражённой и проходящей волн. Используя (11), можно исследовать также условия генерации соответствующих волн в случае ВПЗ-оптического взаимодействия.

Численный анализ и обсуждение

^к mm

a y toA8 0 32 n P _o /

- t WG

E y ² m ( x )d x .

Для численного анализа ВПЗ-оптического взаимодействия в структуре в качестве направляющей среды выбрана плёнка n-GaAs с дисперсией показателя преломления [23]

Система уравнений связи для направляемых встречных мод возмущённого волновода при наличии усиления у [см^-1] имеет вид:

dA /d z = - i к _mmB exp[2 i AP z ] + у A , d B /d z = i к _mmA exp[ - 2 i AP z ] - у B .

f               5,466742 (X / X_o )2

n 2 ( X ) = 5,372514 +  ----- -₂---⁽---- 0L ₊

(            ( X / X 0 ) - 0,4431307 2

0,0242996 ( X / X 0 ) 2

( X / X 0 ) 2 - 0,8746453 2

Здесь безразмерные амплитуды A ( z ) и B ( z ) соответствуют оптическим модам, бегущим соответственно в прямом и обратном направлениях, отстройка констант распространения от резонансного значения 2 AP = 2 P _m - Q . Волновое число ВПЗ обратно пропорционально периоду решетки Л , т.е. Q = 2 п / Л .

+

1,957522 ( X / X 0 )

2 A ^1/2

( X / X 0 ) 2 - 36,9166 2 _?

,

где X - текущая длина волны (в мкм), а X o = 1 мкм. В качестве подложки и покровной среды взят полупро-

водник Al x Ga 1- x As ( x = 0,7), который имеет показатель преломления n 1 ® 3 и сравнительно низкие потери в рабочей области длин волн 1 – 11 мкм [24]. Выбор параметров для плёнки n-GaAs (при комнатной температуре T =300 K) обусловлен требованием фазового синхронизма для встречных мод. Концентрация свободных носителей в плёнке n 0 = 10¹³ см^–3, длина L =0,1 см, т.е. произведение n 0 L = 10¹² см^–2 даёт пороговое значение, при котором в волноводе ещё не происходит развитие неустойчивости доменного типа. Отметим, что для сохранения стабильности ВПЗ могут потребоваться дополнительные меры, например, согласование нагрузочного сопротивления [3, 17]. Подвижность «неразогретых» электронов Ц о = 8500 см²/(В^.с), дрейфовая скорость электронов v ₀ = 2^.10 7 см/с, дифференциальная подвижность ц d = -0,252, коэффициент диффузии D = 207 см²/с [25, 26]; напряжённость статического электрического поля E 0 =4 кВ/см, возмущающее поле E 1 ≈ 400 В/см.

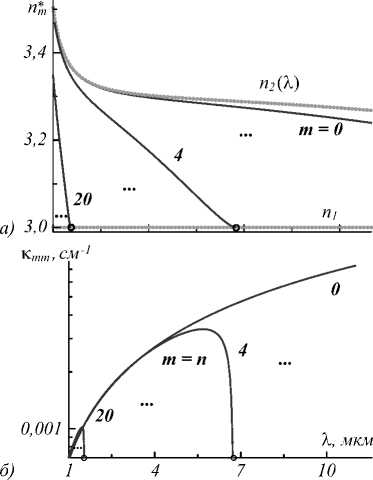
Рис. 2. Зависимости эффективных показателей преломления ТЕ-мод (a) и коэффициентов связи (б) пар одноиндексных (m = n) TE-мод от длины волны в n-GaAs волноводе (параметры структуры см. в тексте)

На рис. 2 представлены зависимости от длины волны эффективных показателей преломления n *m = в m / к ₀ (рис. 2 a ) для трёх мод разных индексов ( m =0, 4 и 20) и коэффициентов связи пар одноин-дексных ( m = n , прямая и обратная) ТЕ-мод (рис. 2 б ). Область существования эффективных показателей преломления определяется разницей значений асимптот n 1 = 3 и n 2 ( X ). Достаточно большая толщина направляющей плёнки t WG = 10 мкм позволяет, с одной стороны, использовать высокоэффективную связь прямой и обратной мод порядка m =0 на длине волны 10,6 мкм, а с другой стороны, стабилизировать распределение ВПЗ вдоль плёнки, избегая образования домена сильного поля [4].

В силу симметрии волновода нулевая мода не имеет отсечки и существует во всей рассматриваемой области длин волн (рис. 2a). С уменьшением длины волны для мод высших порядков наступает режим отсечки, а число распространяющихся мод растёт [20,21]. Общее количество мод можно найти из условия модовой отсечки mmax = { ( tWGk0 Vn2 - ni2 -

- arctan J (n2 - n32)/ (n2 - n2)) / n} int

где “int” означает целую часть выражения. При выбранных параметрах на длине волны X ₀ = 1 мкм максимальное количество мод достигает 37.

Из рис. 2 б видно, что при смещении в длинноволновую область коэффициенты связи мод высших порядков (кроме нулевой) возрастают до максимума, а затем уменьшаются с приближением к отсечке. Наиболее эффективно связываются прямая и встречная моды с индексом m =0, причём их коэффициент связи возрастает при смещении в область больших длин волн. Оптическую накачку в n-GaAs в видимой области (на длине волны X = 0,63 мкм, например) можно осуществить, например, с помощью импульснопериодического лазера на красителе (родамин B) [27]. В данном случае для этого целесообразно использовать CO 2 -лазер. Оценка показывает, что прямая и обратная волны отличаются по частоте на величину частоты ВПЗ Q ~ 10¹¹ c^-1. Отметим, что в реальном эксперименте потери сигнальной волны могут быть сведены к нулю за счёт усиления при рамановском (комбинационном) рассеянии или путём использования узкополосных бриллюэновских усилителей [28,29].

Далее для анализа режимов усиления и генерации были построены изолинии, или контуры равных коэффициентов усиления R = I E r (0) / E i (0) 1 ² для обратной TE 0 -моды (связываемой с падающей TE 0 -модой) (рис. 3) и для прямой ТЕ₀-моды T = | E i ( L )/ E i (0) 1 ² (рис. 4) на плоскости АР L - у L .

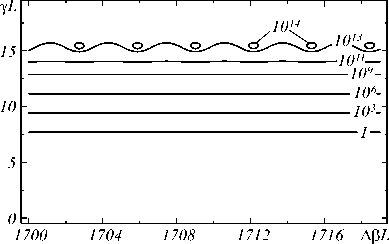
Рис. 3. Контуры равных коэффициентов усиления обратной TE-моды (n = 0) на плоскости Ap L - у L; длина волны А = 10,6 мкм, толщина плёнки t wG = 10 мкм, длина резонатора L = 0,1 см, коэффициент связи к оо = 0,007 см^-1

Из рис. 3 следует, что для возникновения усиления обратной волны по интенсивности (более чем в

1 раз) необходимый уровень оптической накачки должен составлять около 80 см^–1. Генерируемым модам соответствуют центры замкнутых изолиний. Как видно из рисунка, они отстоят друг от друга на величину Δβ L ≈ 3 единицы. Значение коэффициента отражения R в этих областях превышает 10¹⁴. Исходя из выбранных параметров, фазовое рассогласование Δβ составляет приблизительно 1,71 мкм^-1. Это означает, что в данном волноводе возможно осуществить генерацию обратной оптической моды типа TE 0 , которая примерно соответствует третьей справа области замкнутых изолиний на рис. 3.

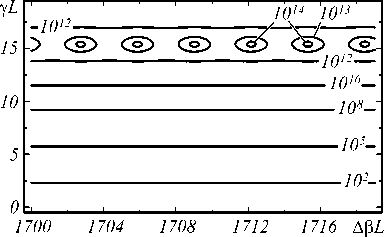
Рис. 4. Контуры равных коэффициентов усиления прямой TE-моды (m = 0) от величин Δβ L и γ L; параметры те же, что для рис. 3

Аналогичный вид имеют контуры равного усиления прямой волны на выходе из резонатора T ( L ), показанные на рис. 4. При усилении γ ≈ 150 см –1 в выбранной области фазовой расстройки генерируется 6 прямых волн, одна из которых соответствует выбранным параметрам (третья справа пара замкнутых изолиний на рис. 4). Таким образом, в результате должной настройки длины резонатора L и подбора материальных параметров волновода можно осуществить одновременную генерацию прямой и встречной лазерных мод на заданной частоте.

Выводы

В ходе проведенного анализа найдены условия усиления и генерации разностного синхронизированного оптического излучения в полупроводниковом волноводе на основе n-GaAs. Обнаружено, что, несмотря на малое значение величины κmmL ≈ 0,001 << 1, на выбранной длине волны (λ = 10,6 мкм) возможна генерация пар встречных TE-мод с одинаковыми индексами (m = n =0) для соответствующей фазовой отстройки ΔβL при условии, что уровень оптической накачки обеспечивает усиление γ порядка 150 см-1. Это сопоставимо с пороговым уровнем усиления (γ ≈ 100 см-1) в гофрированном волноводном лазере [19]. Преимуществом предлагаемой схемы по сравнению с гофрированным волноводным лазером является наличие управляемой ВПЗ-решётки. Настройка разностной частоты ВПЗ может осуществляться путём выбора степени легирования полупроводника, изменения амплитуды и по- лярности внешнего электрического поля E0, а также температурного режима. Полученные результаты могут быть использованы для создания перестраиваемых полупроводниковых лазерных излучателей на основе ВПЗ-оптического взаимодействия.

Работа выполнена при поддержке Министерства науки и высшего образования в рамках выполнения работ по Государственному заданию на НИР №3.8154.2017/БЧ (Д.Г.С., И.С.П.), финансовой поддержке РФФИ, № проекта 19-42-730005 (И.С.П., И.О.З., Д.Г.С.), проекта SPEACS Регионального совета Бретани, Франция (Ю.С.Д.).