Моделирование режимов глобальных электроэнергетических систем

Противоаварийная автоматика (ПА) является важнейшим средством предотвращения и локализации аварийных режимов. Большая протяженность электрических сетей в России, высокая концентрация генерирующих мощностей, удаленность центров производства электроэнергии от центров потребления, необходимость обеспечения надежной работы электроэнергетических рынков обуславливают высокую актуальность противо-аварийного управления в России.

Первый метод противоаварийного управления, изначально реализованный на аналоговорелейной технике как единственно возможный, был перенесен и на первое поколение цифровых устройств ПА. В сущности, он представляет собой таблицу управления, где каждой установке срабатывания автоматики соответствует определенный набор управляющих воздействий (УВ). Это означает, что в процессе определения объема управляющего воздействия не производятся расчеты устойчивости, а осуществляется лишь сравнение текущего режима с некоторыми граничными значениями параметров, требующими той или иной интенсивности УВ. Основные расчеты, необходимые для дозировки УВ, выполняются вне реального времени. Защитные функции таких устройств ПА ограничены не только предусмотренным составом пусковых органов, УВ, контролируемыми параметрами режима, но и тем конкретным перечнем схемных ситуаций, которые мог предвидеть разработчик на стадии проектирования автоматики.

Следующее поколение устройств ПА является адаптивной автоматикой, где объем УВ постоянно пересчитывается в зависимости от схемно-режимной ситуации. Первая версия адаптивного алгоритма противоаварийного управления, в котором решения принимаются непосредственно на основе анализа текущего схемно-режимного состояния контролируемого района применительно к аварийным расчетным возмущениям, была разработана сотрудниками НИИПТ к 1985 г. [1]. На основе программной реализации этого алгоритма сотрудни- ками ОДУ Урала создана Централизованная про-тивоаварийная автоматика (ЦПА). Однако возможности вычислительной техники тогда не позволили реализовать значительное количество блоков алгоритма НИИПТ, в частности касающихся вычисления и оптимизации УВ [2].

В 2005 г. взамен физически и морально устаревшей ЦПА в энергообъединении региона Урала была введена в промышленную эксплуатацию современная Централизованная система проти-воаварийной автоматики (ЦСПА), отличающаяся от предшествующей ЦПА и обладающая безусловными преимуществами. Данные преимущества обусловлены реализацией ЦСПА на современной аппаратной базе с применением современных архитектурных решений и значительным усовершенствованием технологических алгоритмов.

В состав технологических алгоритмов ЦСПА входят:

• •    оценивание текущего режима энергосистемы, результатом которого является модель исходного режима энергосистемы;

• •    прогноз послеаварийного режима энергосистемы, результатом которого является набор переходных и квазиустановившихся режимов в соответствии с заданными аварийными ситуациями;

• •    анализ устойчивости и допустимости после-аварийного режима и выбор управляющих воздействий.

В адаптивном алгоритме ЦСПА задача обеспечения послеаварийной статической устойчивости, разработанном НИИПТ, решается на основе прогноза потокораспределения активной мощности послеаварийного режима (ПАР) [3, 4] и анализа его устойчивости в возмущенных схемно-режимных ситуациях [5, 6]. Для прогноза ПАР используется полная линеаризованная модель энергосистемы.

Методика выбора управляющих воздействий (УВ) для ввода режима в допустимую область подробно описана в [7]. Данная методика основывается на соответствии в пространстве активных мощностей каждому режиму изображающей точки. При последовательно вводимых ступенях УВ изображающая точка будет двигаться от после-аварийного режима к допустимому. Траектория движения изображающей точки будет отражать движение, аналогичное обычно рассматриваемым траекториям утяжеления (облегчения) режима. Очевидно, что результирующий режим не зависит от последовательности ввода отдельных степеней УВ, то есть от траектории движения, а определяется только точкой исходного послеаварийного режима и конечным сочетанием мест и значений УВ. Возможность получения такой траектории, в том числе и за пределами области устойчивости, определяется методом расчета режима по линейной модели исходной энергосистемы. В реальных условиях УВ вводится далеко не во всех узлах, поэтому оптимизация может заключаться только в выборе из конкретного списка тех воздействий, которые дают наибольшее приближение к оптимальному управлению. После выбора места вводится ступень УВ, рассчитывается новый режим по линейной модели энергосистемы и проверяется возможность его существования. Если требуется дополнительное УВ, процесс повторяется относительно новой точки. Данный метод подобен широко используемому градиентному методу наискорейшего спуска. Процесс выбора УВ происходит до тех пор, пока модель не будет находиться в допустимой области.

В данной работе предложен новый вариант адаптивного алгоритма противоаварийного управления, учитывающий изменения опасного сечения (сечения, в котором достигается предельное значение перетока мощности) в процессе поиска УВ. Метод будет основан на последовательном ослаблении перетоков активной мощности между областями, разделенными сильно загруженными по мощности ветвями. Загруженность ветвей в отсутствие устойчивости режима работы сети оценивалась с помощью линеаризованной модели.

I.1. Постановка задачи

Задача поиска УВ состоит в том, чтобы найти оптимальную коррекцию текущих параметров схемы, обеспечивающую сходимость системы уравнений объектов сети, то есть наличие установившегося режима.

Необходимым условием решения задачи является минимизация времени поиска: программа, ищущая УВ, должна работать в реальном времени, следовательно, чем раньше оно будет найдено, тем лучше. Критерии оптимальности найденного УВ могут быть различными: начиная с финансовых соображений (стоимость введения дополнительных мощностей, отключения предприятий и т.д.) и заканчивая соображениями того, что УВ должно было локализовано максимально близко к району возмущения. В разных ситуациях каж-

дый критерий может иметь разный вес, из чего и следует исходить при оптимизации УВ.

I.2. Описание модели и алгоритмов

Расчет установившегося режима. Расчет установившегося режима является неотъемлемой частью задачи построения УВ. В данной работе будет рассмотрена модель энергосети [8, 9], содержащая следующие объекты:

1. Генераторы типа

PQ    U r I r + U i I i = P 0 ,

( -U r I i + U i I r = Q о .

2. Генераторы типа PU

U r I r + U i I i = P 0 , u 2 + u 2 = и о , U r I i + U i I r G [ Q min ,Q max ] .

• 3.    Шунты на землю I = YU, где Y — проводимость на землю.

• 4.    Распределительные щиты Е k = N = Е k = N •B ks/ ₂ , где B k_s — проводимость линии s - k на землю.

5. Линии электропередачи U out — U in = IZ , где Z — импеданс линии.

Трансформаторные линии

I out

U out

= in ,

= U in /k,,

где k — коэффициент трансформации.

Обозначим эту систему (1). При решении ее методом Ньютона [10] в общем виде требуется порядка (2 N + 2 M ) ³ операций на одну итерацию, здесь M и N — соответственно количество ребер и вершин в графе сети. При больших размерах сети время расчетов становится неприемлемо большим, поэтому размерность системы нужно сократить.

Большая часть уравнений линейна, нелинейной является лишь система уравнений для генераторов. Введем вектор так называемых базовых переменных ^u , компонентами которого являются значения напряжения на генераторах сети.

Число уравнений системы (1) 2 N + 2( M g + M s ), где M _s — число узлов, не являющихся генераторами, а M g — соответственно, число узлов-генераторов. Через 2 M g переменных можно выразить оставшиеся 2 N + 2 M s переменные линейным образом, поскольку число линейных уравнений также 2 N + 2 M s . Получаем в результате систему уравнений вида:

1. Генератор s , типа PQ :

U sr

k = M g k =1

^{( a} skr ^U kr ^{+ e} skr U ki ^{) +}

+ U si Е k=M g ( a ski U kr + e ski U ki ) = P s о , U si Е k =1 g ^{( a} skr U kr ^{+ e} skr ^U ki ) ^—

^U sr ^^k =1 ^{( a} ski ^U kr ^{+ e} ski ^U ki ) = Q s 0 .

• 2.    Генератор s , типа PU :

U sr E k =1 ^{( a} skr U kr + ^e skr U ki ) +

+ U si E kM g ( a ski U kr + e ski U ki ) = P s о , U 2i + U s ² r = U s о ,

Qs E [ Qmin ,Qmax], где αskγ и βskγ — коэффициенты выражения тока генератора s через UkY, Y = {r,^}, то есть соответственно коэффициенты при вещественной или мнимой части.

Таким образом, размерность системы (1) сокращена до 2 M g .

Для решения такого рода систем хорошо подходит модифицированный метод Ньютона (далее ММН) [5], который для уравнения f ( X ) = 0 ищет решение в виде: X „ ₊i = X n + a d^Xx) f ( X n ), где a = argmin( If ( X n +1 ) | |) . Этот метод умеренно требователен к начальному приближению.

Поиск начального приближения осуществляется следующим образом: решается некоторое линейное приближение системы (1), а затем полученное решение уточняется методом Ньютона. В за- висимости от ситуации используются следующие линеаризации.

• 1.    Для генераторов типа PQ :

  S s U s ^∗ |U s | ²

  
  

• 2.    Для ветвей: P ki = U k ||U i | * H i | * ( 5 k — 5 i ), где δ _s — фаза напряжения s -го генератора, а σ kl — коэффициент трансформации, деленный на реактивное сопротивление ветви. Для узлов справедлив закон сохранения энергии: E k= ^M s P sk = P s . Если считать напряжения постоянными и равными либо номинальным, либо напряжениям предыдущего уже посчитанного режима (в случае расчета режима после возмущения), то получается линейная система уравнений для {5} и {P} , которая достаточно просто решается в связи с её разреженностью. Ее решением и является требуемое распределение потоков мощности для начального приближения.

k = M g

= E ( Y k U k ) .

k =1

При использовании этой линеаризации для генераторов типа PU (для которых реактивная мощность лежит в заданных границах) требуется выбрать Q , входящую в соответствующую s . Считается, что |U _s |,s E PQ (то есть s из множества генераторов типа PQ ) постоянно с некоторой точностью. Как показали вычислительные эксперименты, если число PU генераторов мало, то при использовании ММН получается хорошее начальное приближение.

Для поиска режима текущей конфигурации схемы находится режим близкой конфигурации, а затем линейным приращением параметров получается требуемый. А именно, пусть П — вектор параметров системы, в которой ищется режим. Тогда находим из известных нам векторов П k , к = 1 , 2 , ..., K вектор П _x такой, что П _x = argmin( || П — П l |||V П l ). Далее решаем следующий набор задач: для каждого к = 1 , 2 , ..., K П temp ( к ) = П( k/K ) + П _x (1 — k/K ) находим установившийся режим для схемы П temp ( к ), принимая за начальные значения решение предыдущей схемы П temp ( к — 1), к = 2 , ..., K .

Поиск управляющего воздействия.

Предположим наличие какого-нибудь базового режима работы сети, тогда аварийная ситуация есть возмущение параметров этого режима. Приведем базовый режим к аварийному аналогично методу № 3 поиска начального приближения. Корректировки, полученные в результате, и будут искомым УВ.

Опишем процесс подробнее. Пусть П — набор параметров схемы, а П — их корректировка (УВ). Тогда итерационная схема выглядит следующим образом: П( к ) = П end (- ^ ) + П _о (1 — -K ) + П( к ), к = 0 , 1 , 2 ,...,K , где П( к ) = 0 при к = 1 и П( к ) = П( к — 1) + П( к ) при к >  1, здесь П( к ) — корректировка текущего набора параметров, требуемая для сходимости схемы.

Находится П( к ) так: пусть при некотором П режим отсутствует, тогда решаем систему оценочных уравнений

I e i = Г ^з P ij = а P j ,

I P ij = |U j ||U i ||^ ij | ( 5 i — 5 j ) .

Получаем послеаварийное распределение активной мощности на схеме и находим опасные сечения, которые необходимо устранить. Эти сечения разбивают граф на подграфы, в каждом из которых поток мощности критичен. Понижаем эти перетоки за счет самых мощных узлов в каждом подграфе, то есть уменьшаем P _нагр или P _ген у генератора с соответствующим максимальным показателем. Шаг изменения выбираем таким, чтобы появились дополнительные подграфы, построенные указанным выше способом. Повторяем, начиная с поиска опасного сечения.

Как показала практика, для схем порядка 100 генераторов количество таких итераций порядка 2--3.

Найденное таким образом «грубое» УВ приводится к оптимальному виду — уменьшается насколько возможно — с помощью следующего алгоритма:

• 1.    Находится опасное сечение.

• 2.    Находятся два узла из УВ с максимально уменьшенными соответственно потреблени-

• ем и генерацией, если такие есть по одну сторону от сечения.

• 3.    Увеличивается соответствующий переток, причем контролируется появление новых опасных сечений.

Особенности программной реализации. Разработанная на основе описанных в предыдущем разделе алгоритмов программа PCDU_D6 позволяет рассчитывать установившийся режим заданной сети, а в случае его отсутствия — искать УВ.

Одной из основных особенностей реализации является возможность многопоточных расчетов на многопроцессорных системах, причем настройка по количеству процессоров производится автоматически. Для расчета установившегося режима это позволяет одновременно проверять несколько начальных приближений метода Ньютона, а для вычисления УВ — использовать сразу несколько алгоритмов.

Как было сказано ранее, поиск УВ должен быть выполнен за как можно меньшее время. Поэтому еще до проведения оптимизации его некоторое найденное приближение выводится на экран.

Для каждой стадии поиска возможно использование нескольких алгоритмов. В зависимости от выбора, изменяется траектория внутри допусти- мого множества состояний системы при оптимизации, а также шаг релаксации, рассчитанный на скорость поиска, минимальность и т.д. Критерии оптимизации в данной программной реализации были настроены на уменьшение УВ.

II. Результаты расчетов

Расчеты были проведены на ряде тестовых схем, а также на реальной схеме ОДУ Урала. Дано сравнение с результатами расчетов, полученных при помощи ПК RastrWin [11].

Расчет 1. Исследовались четыре схемы одинаковой топологии (рис. 1) с разными значениями параметров нагрузки и генерации. Использовалось наведенное возмущение: отключение линии 4 → 5. В таблицах 1, 2, 3 и 4 приведены параметры режима и необходимое для устойчивости УВ (показано стрелкой). Рассматривались четыре случая.

Рис. 1. Схема для расчета 1

Таблица 1

№	P г , МВт	Q г , МВт	Q min , МВт	Q max , МВт	P н , МВт	Q н , МВт	U ном , кВ
1							500
2	Базовый						510
3							500
4	1000		- 300	+300	200	100	514
5					1500 → 1000		504
6	400		- 500	+500	100	100	228
7					100	50	225
8			- 100	+100	100	100	225
9					100	200	225

Таблица 2 4  1500 → 1300      - 300  +300  200  100  514 5                                   800        504 6  400              - 500  +500  100  100  228 7                                   400 50   225 Таблица 3
4	1500 → 1200		- 300	+300	200	100	514
5					1500 → 900		504
6	400		- 500	+500	100	100	228
7					100	50	225
Таблица 4
4	2000 → 1300		- 300	+300	200	100	514
5					1500 → 1100		504
6	800		- 500	+500	100	100	228
7					100	50	225

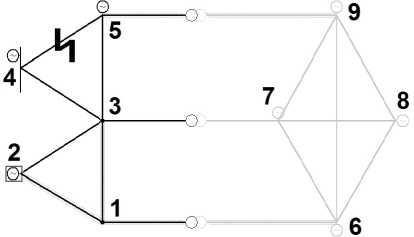
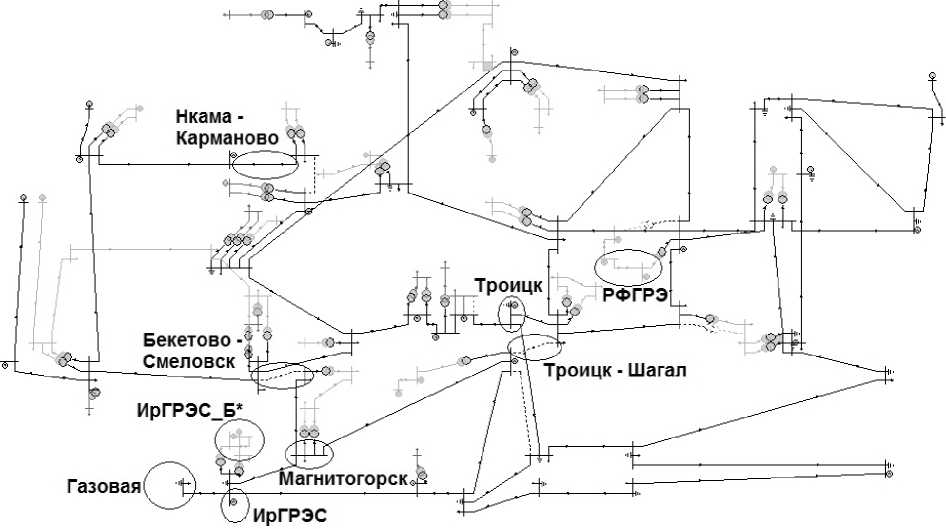
Рис. 2. Схема для расчета 2

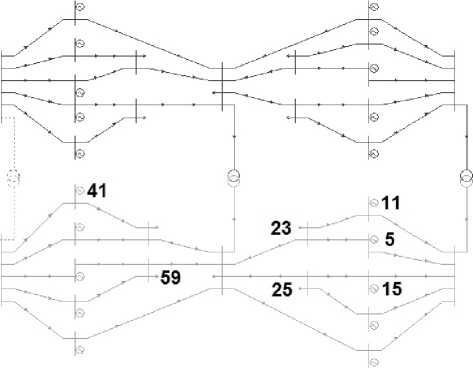
Рис. 3. Схема для расчетов 3.1, 3.2

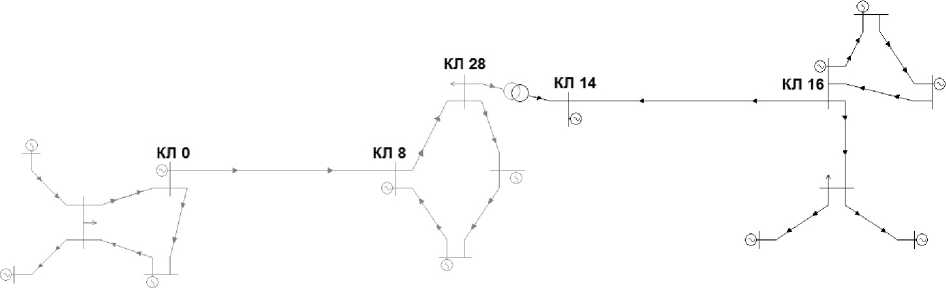
Рис. 4. Схема для расчета 4

• 1.    Нарушение устойчивости по линии 3 → 5. (Далее в таблицах будут приведены только различия со случаем № 1).

• 2.    Нарушение устойчивости по совокупности линий 3 → 5 и 3 → 4.

• (a) Нарушение устойчивости по линии 3 → 4.

• (a) Нарушение устойчивости по совокупности линий 3 → 5 и 3 → 4.

Расчет 2. Была исследована работа алгоритма на больших схемах. В качестве тестового примера использовалась реальная схема ОДУ Урала (рис. 2). Рассматривалось два случая.

• 1.    Возмущение исходного режима:

• •    отключение линии «Бекетово — Сме-ловск»,

• •    отключение линии «Нкама (Удмуртия) — Карманово»,

• •    отключение линии «Троицк — Шагал»,

• •    увеличение генерации для «Троицк» на 2000 МВт,

• •    увеличение потребления для «РФГРЭ» на 2000 МВт.

• 2.    Возмущение исходного режима:

• •    отключение линии «ИрГРЭС — Газовая»,

• •    отключение линии «ИрГРЭС — Магнитогорск»,

• •    отключение линии «ИрГРЭС — ИрГР-ЭС_Б1»,

• •    отключение линии «ИрГРЭС — ИрГР-ЭС_Б2»,

• •    увеличение генерации для «ИрГРЭС» до 2700 МВт.

В первом случае нарушается устойчивость по линиям, соединяющим основную часть схемы с «Троицк» и «РФГРЭ». Таким образом, получается три изолированных подграфа. Понижая одновременно генерацию в «Троицк» и потребление в «РФГРЭ», получаем следующее УВ: понижение генерации в «Троицк» на 100 МВт и потребления в «РФГРЭ» на 200 МВт.

Во втором случае нарушается устойчивость по линиям, соединяющим основную часть схемы с «ИрГРЭС». Таким образом, получается два изолированных подграфа. Восстанавливая устойчивость на соответствующей линии, получаем УВ в «ИрГРЭС» — уменьшение генерации на 1700 МВт.

Расчет 3.1. Искались предельные режимы по заданным векторам изменения режима (ВИР) для выбранных генераторов (рис. 3), то есть ступенчато увеличивались мощности генерации до тех пор, пока режим сохранял устойчивость.

• 1.    Повышение генерации на 15-м и 23-м генераторах:

PCDU_D6: Δ P 15 = 570 МВт, Δ P 23 = 270 МВт;

RastrWin: Δ P 15 = 560 МВт, Δ P 23 = 260 МВт.

• 1.    Повышение генерации на 11-м, 25-м, 59-м генераторах:

PCDU_D6: Δ P 11 = 490 МВт, Δ P 25 = 190 МВт, Δ P 59 = 190 МВт;

RastrWin: Δ P 11 = 450 МВт, Δ P 25 = 150 МВт, Δ P 59 = 150 МВт.

• 1.    Повышение генерации на 5-м и 41-м генераторах:

PCDU_D6: Δ P 5 = 162 МВт, Δ P 41 = 320 МВт;

RastrWin: Δ P 5 = 150 МВт, Δ P 41 = 310 МВт.

Расчет 3.2. Режим выводился на предел, после чего добавлялось утяжеляющие воздействие в сторону увеличения перетоков (отсчет Δ P идет от соответствующих предельных режимов, найденных в расчете 3.1). Искомое УВ должно было скомпенсировать утяжеляющий ВИР с точностью допустимого шага (ступени генерации — 100 МВт в тестах). Заметим, что при расчете величины УВ в RastrWin шаг по генерации соблюдать не обязательно, поэтому просто искалось минимальное изменение, необходимое для стабилизации режима по вектору, найденному в PCDU_D6.

• 1.    Повышение генерации на 15-м и 23-м генераторах: Δ P 15 = 30 МВт, Δ P 23 = 30 МВт.

PCDU_D6: Δ P 15 = - 100 МВт;

RastrWin: Δ P 15 = - 70 МВт.

• 1.    Повышалась генерации на 11-м, 25-м и 59-м генераторах: Δ P 11   =60МВт,

Δ P 25 =60 МВт, Δ P 59 =60 МВт.

PCDU_D6: Δ P 11 = - 300 МВт;

RastrWin: Δ P 11 = - 220 МВт.

• 1.    Повышение генерации на 5-м и 41-м генераторах: Δ P 5 =40 МВт, Δ P 41 =40 МВт.

PCDU_D6: Δ P 5 = - 100 МВт;

RastrWin: Δ P 5 = - 70 МВт.

Расчет 4. Исследовались пропускная способность ребер, соединяющих ключевые части системы: КЛ0 — КЛ8, КЛ14 — КЛ16 (рис. 4), существование режима в зависимости от сопротивления тех же линий, а также УВ при отключении в исходном режиме линии КЛ8 — КЛ28 высокой проводимости.

• 1.    Поиск предельных перетоков на линии КЛ0 — КЛ8.

PCDU_D6: - 589 . 1 + j 11 . 2 МВт;

RastrWin: - 616 . 1 - j 4 . 4 МВт.

• 1.    Поиск предельных перетоков на линии КЛ14 — КЛ16.

PCDU_D6: 296 . 3+ j 203 . 5 МВт;

RastrWin: 308 . 7 + j 131 . 8 МВт.

• 1.    Поиск максимального сопротивления линий КЛ0 — КЛ8, КЛ14 — КЛ16 (совпадает с точностью до 0 , 1 Ом в RastrWin и PCDU_D6).

КЛ0 — КЛ8: 9 , 40 + j 34 , 80 Ом;

КЛ14 — КЛ16: 19 , 20 + j 34 , 20 Ом.

• 1. Поиск УВ при отключении линии большой проводимости КЛ8 — КЛ28.

PCDU_D6: A P _{КЛ 16} = - 100 МВт;

RastrWin: A P _{КЛ 16} = - 48 МВт.

На основе тестовых расчетов можно сделать следующие выводы.

• 1.    С точки зрения расчета установившегося режима система PCDU_D6 дает результаты, в большинстве случаев практически не отличающиеся от результатов расчета системы ПК RastrWin. Различие обусловлено тем, что используются различные начальные приближения для поиска решения, а значит, и разные траектории поиска. Когда результаты отличались, проводилась следующая проверка: режим, найденный в PCDU_D6, задавался в RastrWin как начальное приближение. После этого за 1--2 итерации RastrWin сходился к этому же режиму в том смысле, что за 2 итерации решение практически не менялось относительно начального.

• 2.    Режим, полученный в PCDU_D6 после применения УВ, и режим, найденный в RastrWin при движении по вектору УВ, совпадают с точностью до шага поиска УВ.

• 3.    PCDU_D6 находит УВ менее, чем за 5 секунд на стандартном PC (частота процессора примерно 3 ГГц, объем оперативной памяти примерно 1 Гб).

Заключение. В работе рассмотрена модель энергосистемы и описан алгоритм поиска УВ, имеющий ряд нововведений по сравнению с существующими. В частности, добавлена проверка опасных сечений в процессе поиска и возможность релаксации одновременно нескольких сечений. Также введена оптимизация УВ по различным критериям, причем добавление новых не составляет труда.

При программной реализации метода использованы преимущества многопроцессорных систем.

Алгоритм проверен на ряде различных схем. Сравнение по каждому из режимов с ПК RastrWin показало, что разработанный метод находит оптимальное УВ.

Тестирование предложенной модели, реализованной в виде программного комплекса

ТРУДЫ МФТИ. — 2010. — Том 2, № 3 PCDU_D6, продемонстрировало её пригодность для решения практических задач.

Работа проведена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009--2013 годы и поддержана грантом РФФИ № 08-07-00429-а.