Моделирование резинокордных слоев при квазистатическом нагружении
Автор: Шешенин С.В., Икунь Ду, Чистяков П.В., Артамонова Н.Б.
Статья в выпуске: 4, 2021 года.
Бесплатный доступ
Моделирование пневматической шины при сильном изменении формы вызывает проблему выбора адекватной модели резинокордных слоев. Классическая методика осреднения, вообще говоря, не подходит в силу физической и геометрической нелинейности при рассматриваемом деформировании до 15 %. В работе кратко приводятся известные варианты моделирования всей шины и резинокордных слоев. Делается выбор в пользу описания резинокордных слоев с помощью потенциала напряжений, являющегося анизотропной функцией инвариантов тензора деформаций. Из такого определяющего соотношения следует квазилинейное соотношение в терминах дифференциалов напряжений и деформаций. Также поясняется удобство этих двух типов определяющих соотношений для численной реализации. Описана модификация определения эффективных свойств неоднородного слоя. Поясняется отличие от стандартного определения эффективных модулей. Считается, что расположение кордных нитей приближенно можно считать периодическим, а все нити заменить эффективным волокном. При этих предположениях описаны две модели резинокордного слоя: модель ортотропного материала и модель трансверсально-изотропного материала. Указано на схемы вычислений, которые можно считать вычислительными экспериментами, позволяющими определять материальные параметры анизотропных потенциалов. Описаны проведенные реальные эксперименты с пластиной из брекерной резины при медленном квазистатическом растяжении. Обнаружен существенный гистерезис. Показано, что аддитивная модель, сочетающая гиперупругий материал с линейной моделью Максвелла, описывает зависимость от скорости деформирования. Описана использованная схема численного решения квазистатической задачи деформирования шины, которая реализована в виде собственной программы. Описаны верификационные тесты. Приведен пример деформирования шины, так называемый тест на разрыв, в котором осуществляется сильное деформирование и применяется разработанная модель.
Пневматическая шина, резинокордный слой, эффективный анизотропный гиперупругий материал, ячейка периодичности, модель ортотропии, модель трансверсальной изотропии, эффект гистерезиса, свойство вязкоупругости, модель максвелла, собственная численная реализация, тест пневматической шины на разрыв
Короткий адрес: https://sciup.org/146282382
IDR: 146282382 | УДК: 539.3 | DOI: 10.15593/perm.mech/2021.4.06
Modeling of rubber-cord layers under quasi-static loading
Modeling a pneumatic tire with a strong change in shape causes the problem of choosing an adequate model for rubber-cord plies. Generally, the classical method of asymptotic homogenization is not suitable due to physical and geometrical nonlinearity for the strain up to 15 %. The known models used for simulation the entire tire as well as rubber-cord plies are analyzed. A choice is made in favor of modeling the plies using the stress anisotropic potential, which is an anisotropic function of the strain tensor invariants. The relationship of such a constitutive law with a quasi-linear constitutive equation in terms of stress and strain differentials is indicated. A convenience of these two types of constitutive equations in terms of numerical implementation is also given. A modification of the effective properties definition for an inhomogeneous layer is explained. The difference from the standard effective moduli definition is clarified. The arrangement of the cords is supposed to be approximately periodic and all cords to be equivalent to the effective fiber. Two models of a rubber-cord plies are described under such assumption. These are a model of an orthotropic material and a model of a transversely isotropic material. Computational experiments, which make it possible to determine the material parameters of anisotropic potentials, are pointed out. Real tests with a sample of rubber ply under slow quasi-static loading were conducted. Significant hysteresis was detected. It is shown that an additive model combining a hyper elastic material with Maxwell viscoelastic model provides good accuracy in stress dependence on the strain rate. The numerical procedure developed to calculate solution to the quasi-static problem of tire deformation is described. It is implemented in home-made computer code. A numerical example on the tire simulation is given. That is so-called breaking test, in which strong deformation is achieved and the developed model is applied to.
Текст научной статьи Моделирование резинокордных слоев при квазистатическом нагружении
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2021PNRPU MECHANICS BULLETIN
Моделирование (или расчет) шин имеет давнюю историю, на протяжении которой существенно усложнялись предлагаемые модели [1]. Были модели, которые рассматривали шину как систему кольца и пружин. Можно вспомнить работы немецкого специалиста Ф. Бема (см., например, [2]), в которых он предложил так называемую mass-point-модель. Шина моделировалась как ансамбль массовых точек, связанных пружинами, формирующими объект, по форме напоминающий шину. Эта модель, интересная с точки зрения истории, приводит к системе обыкновенных дифференциальных уравнений и годится для описания волновых, т.е. «быстрых», процессов в шине при качении или ударе. Это так называемая явная динамика. Для описания стационарного качения и «медленных» переходных процессов (медленная динамика) эффективнее неявные методы интегрирования по времени, например метод Ньюмарка [3]. Если скорость деформирования достаточно мала, то инерционным членом можно пренебречь. Именно такой класс задач рассматривается в данной работе.
Был период времени, когда использовались различные теории многослойных оболочек [4, 5], хотя переход к методу конечных элементов [6–13] был неизбежен. Здесь, конечно, приведено минимальное количество работ. Вначале использовались достаточно простые модели для описания внутренней структуры шины, которая, однако, достаточно сложна. В радиальной шине, помимо нескольких слоев резинокорда, имеются области, существенно различающиеся сортами резины. Поэтому для адекватного описания структуры шины какая-либо теория оболочек вряд ли подходит.
Здесь уместно перечислить трудности с точки зрения механики или вычислений, встречающиеся при моделировании квазистатических или медленных динамических процессов в шине. Как пример будем иметь в виду радиальную шину легкового автомобиля, состоящую из двух резинокордных слоев брекера и слоя каркаса. Прежде всего, речь идет о резине, которая скрепляет резинокордные слои и реализует контакт с дорогой. Этот материал обладает малой сжимаемостью, и, следовательно, возникает дилемма – либо формулировать задачу в перемещениях, либо использовать смешанную постановку. Наличие анизотропных слоев указывает на преимущество использования постановки чисто в перемещениях, чтобы все части шины дискретизировались одинаково. Во-вторых, нужно отметить, что резинокордные слои являются сильно анизотропными. Материал шины в целом является также сильно неоднородным. Поэтому конечно-элементная система уравнений не является простой для решения.
Расчет шины может осуществляться с различными целями, поэтому используемые модели могут быть раз- личными. Например, для моделирования сцепления с дорогой важными являются модель трения (например закон трения Кулона) и алгоритм решения контактной задачи. В задачах тепловыделения важны вязкоупругие свойства применяемых резиновых смесей и резинокордных слоев. Кроме этого, важны закон обмена теплом на внешней и внутренней границах и описание движения воздуха внутри шины.
В нашей работе рассматривается сильное деформирование шины под действием внешней нагрузки. Типичным примером является так называемый тест на разрыв (Breaking Test). Тест состоит во внедрении в шину индентера в радиальном направлении вплоть до разрыва или контакта с ободом (рис. 1).
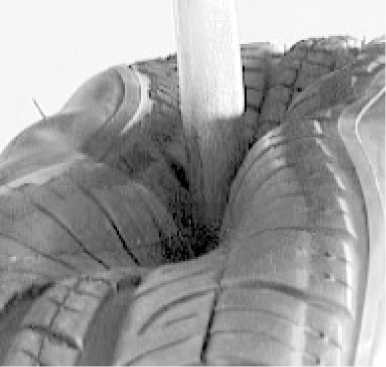
Рис. 1. Тест на разрыв. Процесс внедрения индентера в шину
Fig. 1. Breaking test. The process of the indenter penetration into the tire
Зависимость вдавливающей силы от перемещения ин-дентера является результатом испытания. В опыте осуществляется сильное изменение формы шины, т.е. проблема является существенно геометрически нелинейной. Процесс вполне можно считать квазистатическим, а материал резины можно предполагать гиперупругим. Подробнее об этом пойдет речь в разделе 4. Вопрос о модели резинокордных слоев рассматривается в разделе 1.
Существует несколько подходов для конечноэлементного моделирования резинокордных слоев. Один из них состоит в моделировании кордных нитей и окружающей матрицы из резины. Можно подсчитать, сколько примерно конечных элементов потребуется только для дискретизации нитей корда одного брекер-ного слоя при трехмерных конечных элементах. Если считать, что длина развертки шины 2 м и ширина слоя брекера 20 см, кордный угол 25°, а расстояние между нитями 1 мм, то получаем, что длина корда одного бре-керного слоя равна примерно 1 км. Если выбрать длину конечного элемента также 1 мм, то число элементов для дискретизации волокон одного слоя равно 1 млн. Это если считать, что волокно дискретизируется одним элементом в поперечном направлении. Дискретизация матрицы увеличит это число в несколько раз. Поэтому де- тальная дискретизация одного резинокордного слоя потребует несколько миллионов элементов. Нелинейный анализ такой большой системы в настоящее время затруднителен. При этом вряд ли можно надеяться на помощь параллельных вычислений. Система с разряженной матрицей не обладает эффективностью при распараллеливании. Известно, что бывает эффективнее использовать два процессора вместо обычно доступных четырех, не говоря уже о десятке процессоров. Речь, конечно, идет о неявных методах интегрирования конечно-элементных (КЭ) уравнений по времени (или параметру нагружения). Поэтому следует остановиться на использовании осредненных свойств резинокордных слоев.
В этом подходе имеются варианты. Один из них состоит в осреднении на уровне конечного элемента [13]. Другими словами, рассматриваются элементы, имеющие внутри себя кордные нити, которые учитываются при построении матрицы жесткости. Специфика такого подхода состоит в том, что эти нити модельные, их число определяется числом конечных элементов и вовсе не совпадает с числом реальных нитей кода. Такой подход известен с ранних этапов развития метода конечных элементов (МКЭ). Ниже рассматривается другой подход (см., например, [8, 14–15]), в котором находятся осредненные свойства резинокордного слоя до конечноэлементной дискретизации.
1. Определяющие соотношения резинокордных слоев
Часто в задачах о качении шины резинокордные слои моделировались как геометрически и физически линейные [1]. В силу специфики рассматриваемых нагружений мы предполагаем слои физически и геометрически нелинейными. Можно использовать соотношение гиперупругого материала dw (x, c ) _ aw (x, c)
P =-------- или S = 2--------
.
d F
d C
Здесь и далее используем обозначения [16]: T – тензор напряжений Коши, P = J F - 1 • T - первый тензор напряжений Пиолы - Кирхгофа, J = det( F ) - якобиан преобразования Пиолы, S = J F - 1 • T • F - второй тензор Пиолы - Кирхгофа, C - тензор Коши - Грина ( С = F T • F , F - деформационный градиент) и E = 1 / 2( C - 1 ) -Лагранжев тензор деформаций. Соотношение (1) удобно тем, что в одинаковой форме выглядит как для областей резины, так и для резинокордных слоев. В первом случае потенциал подходит в виде Муни – Ривлина
W shear = С 10( 1 1 - 3) + c 01( I 2 - 3) + + c 20 ( I . - 3)2 + С зо ( I 1 - 3) 3 ,
где 1 1 , 1 2 , 1 3 - инварианты тензора C = F T • F , F = F / J1/3. Это «сдвиговая» часть потенциала. «Объемная» часть имеет, например, вид
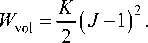
Тогда W iso = W shear + W vol. Во втором случае требуется использовать потенциал анизотропного материала. Использование потенциала (2) в самом начале процесса нагружения нецелесообразно, поэтому можно использовать квадратичный потенциал
W = 1(Х + 2Ц)( I , - 3) 2 + ц( 1 1 - 3) - Н( 1 2 - 3), 82
Н = 2( C 01 + C w).
Во втором случае структура потенциала от набора инвариантов зависит от типа анизотропии и описана, например, в [17]. Так, в случае ортотропии независимыми инвариантами относительно группы преобразований ортотропии являются инварианты: C αα , C αβ , а * в, а,в = 1,2,3 [17].
Вообще говоря, потенциал можно выбирать как функцию от набора инвариантов, который удобен для использования. В соответствие с этим, эффективный потенциал резинокорда W представим в виде изотропной части и корректирующих членов:
eff iso corr.
Изотропную часть выберем в виде потенциалов Муни, когда в (2) c 20 = 0, c 30 = 0, или Трелоара, когда в (2) c 01 = 0, c 20 = 0, c 30 = 0 , учитывая, что деформации в резинокорде не превышают 15–20 %.
Для ортотропных материалов число независимых инвариантов равно шести [17]. Однако в выражении потенциала часто для удобства используют зависимые инварианты. Для описания потенциала ортотропного материала к инвариантам I 1 , I 2 , I 3 можно добавить инварианты I 41 , I 42 и I 5 , I 6 :
Г41 = 2 C 13 , 1 42 = 2 C 223 , 1 5 = 2 ( C 33 - 1 ) 2 , I 6 = j ( C 22 - 1 ) 2 .
Следовательно,
Wef = Wsh + Wvol + W h . + Wsh_2 + W33 + W22, где Wh = a2 I. , Wsh_2 = a23142
потенциальная
энергия сдвига вдоль волокон в плоскостях 1–3 и 2–3, а W33 = "2315, W22 = "22"16- Таким образом, рассматри- ваемый потенциал ортотропной среды имеет шесть (или семь, если используется потенциал Муни) материальных параметров: c10, (c01), K, a13, a23, b33, b22 . Для их определения требуются либо эксперименты с образцами резинокордного материала, либо численное решение задачи на ячейке.
В ряде случаев материал слоя можно описывать как трансверсально-изотропный. Тогда вид потенциала упрощается
Wef = Wiso + Wtr_sh + Wtr_tens, где Wtr sh = 214 — это потенциальная энергия сдвига
вдоль волокон, а W tr tens = — 1 5 - это потенциальная энергия растяжения/сжатия в третьем направлении. При этом
1 4 = 2 ( C 1 2 3 + C 223 ) , 1 5 = 2 ( C 33 - 1 ) 2.
Таким образом, рассматриваемый потенциал трансверсально-изотропной среды имеет четыре или пять материальных параметров: c 10 , ( c 01 ), K , a , b .
2. Осреднение резинокордных слоев
Независимо от используемой структуры потенциала, он описывает осредненные свойства резинокордного слоя. Поэтому требуется иметь точное определение эффективных упругих свойств и представительной области (RVE) в случае неоднородного слоя.
В случае трехмерной среды одно из первых определений представительной области (RVE) представлено Хиллом [18, 19]. В [20] было дано строгое определение эффективных модулей упругости, обобщенное затем для нелинейных моделей МДТТ [15, 21, 22].
Асимптотический подход развивался при анализе периодических сред как в трехмерном случае [21, 23–25], так и в случае неоднородных слоев [26–27, 31]. В [28, 29] двухслойный резинокордный ламинат был проанализирован в рамках линейной упругости. Следует отметить, что в большинстве работ определяются двумерные эффективные определяющие соотношения в предположении плоского напряженного состояния слоя. К этому приводит асимптотический подход, так же, как и классическая ламинатная теория (КЛТ) (см., например, [26, 27, 30, 31]). Последнее неудивительно, поскольку КЛТ является просто первым приближением асимптотического разложения [31].
Однако для анализа НДС в рамках 3D-конечно-элементной модели требуется знать модули в поперечном направлении. В работах [15, 22, 32] отмечается, что стандартное определение эффективных свойств для трехмерной среды некорректно для слоя, поскольку в поперечном направлении нет представительной области. Другими словами, краевой эффект пронизывает всю ячейку периодичности. В [15, 22] предложены обобщения определений представительной области и эффективных свойств для слоя, окруженного однородной средой, пригодные как для линейной, так и нелинейной упругости. Идея состоит во включении в представитель- ную область (ячейку периодичности) окружающего материала. Это первая отличительная черта, которую необходимо учитывать при определении эффективных свойств слоя. Здесь следует подчеркнуть, что речь идет именно об определении эффективных свойств. Способы приближенного вычисления рассматриваются ниже.
Заметим, что имеется вторая особенность, касающаяся эффективных свойств слоя. Дело в том, что определение эффективных свойств, предложенное в [15, 22], есть определение именно жесткостей (или модулей) в плоскости слоя, но не изгибных жесткостей. В случае трехмерной среды этого вполне достаточно, но не в случае слоя, который характеризуется как жесткостями в плоскости слоя, так и изгибными и крутильной жесткостью. Однородный слой с правильными двумерными модулями в плоскости слоя может обладать изгибными жесткостями, не соответствующими изгибным жесткостям осредняемого неоднородного слоя. Поэтому не случайно, что метод осреднения [27, 31] одновременно понижает размерность задачи, сводя трехмерный слой к модели пластины, а также позволяет определять как жесткости в плане, так и изгибные и крутильную жесткости. В соответствие со сказанным, изгибные жесткости, вообще говоря, не могут быть получены из осред-ненных двумерных жесткостей в плане слоя.
Для исправления ситуации возможны по крайней мере два подхода. Первый вариант более «научный». Рассмотрим лишь его схему. Известно, что при применении второго приближения [31] для неоднородного линейного упругого слоя результатом является теория пластин, эквивалентная теории Миндлина – Рейснера. С другой стороны, согласно работе [33], применение первого приближения для однородного слоя, подчиняющегося линейной моментной теории упругости, приводит также к теории типа Миндлина – Рейснера. Таким образом, с помощью асимптотических разложений наблюдается эквивалентность между неоднородным слоем с линейно упругим материалом и однородным слоем с линейно моментным упругим материалом. Следовательно, неоднородный слой следует описывать однородным моментным материалом, чтобы адекватно описать свойства на растяжение/сдвиг и свойства на изгиб/кручение.
Однако существует более простой «инженерный» способ моделирования неоднородного слоя эквивалентным однородным в рамках обычной линейной теории упругости. А именно, можно применить так называемое «обрезание» резинокордного слоя. Это означает, что слой в конечно-элементной модели искусственно делается более тонким, чем реальный резинокордный слой. При этом его толщина подбирается так, что жесткость на растяжение в направлении волокон и изгиб относительно поперечной оси были такими же, как соответствующие жесткости исходного неоднородного слоя. Поскольку отмеченные жесткости существенно больше остальных соответствующих жесткостей, то такой подход вполне уместен.
3. Задачи на ячейке
Как уже отмечалось, для резинокордного слоя стандартное определение осредненных упругих свойств [21], строго говоря, не подходит [15, 22]. Это определение предполагает наличие представительной области, чтобы краевой эффект не влиял на расчет эффективных свойств. Однако в случае резинокордного слоя краевой эффект пронизывает всю ячейку периодичности, показанную на рис. 2, а . Это приводит, в частности, к тому, что вычисленные согласно классическому определению эффективные модули линейной упругости не являются обратными к эффективным податливостям. Поэтому определение осредненных упругих свойств нуждается в изменении.
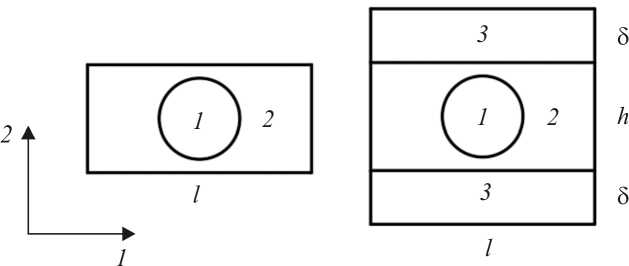
Рис. 2. Модельная ячейка периодичности резинокордного слоя (RVE) ( а ); расширенная ячейка (RVE+) ( б )
Fig. 2. Model cell of the rubber-cord ply periodicity cell (RVE) ( а ); modified model cell of the rubber-cord ply periodicity cell (RVE +) ( б )
Чтобы это сделать, ячейка сверху и снизу дополняется слоями однородного материала, который окружает неоднородный слой в конструкции. Эта схема показана на рис. 2, б . Так, получается ячейка RVE+, которая состоит из материала корда 1 , материала матрицы 2 и материала 3 , окружающего резинокордный слой. Идея модифицированного определения [15, 22] эффективных упругих свойств состоит в том, что аффинное преобразование начальных координат в текущие задается на границе области RVE +, а средние напряжения и деформации вычисляются по области RVE
-
(S) = — S dV, (C) = — C dV.
VRVE V RVE VRVE V RVE
На боковой поверхности ячейки периодичности задаются условия, учитывающие периодичность НДС, описанные подробно в [22].
Предполагается существование эффективных потенциалов, таких, что d Wef «C) ,C =d wf « S d(C) , / d(S)
В [22] описаны схемы проведения вычислительных экспериментов, которые позволяют вычислить все материальных параметры упругих потенциалов в случаях трансверсальной изотропии и ортотропии. Проведенные вычисления показали, что необрезанный слой, для кото- h рого n = ~
может моделироваться как трансвер- сально-изотропный. Обрезанный слой (n « 0,5 ) следует рассматривать как ортотропный, причем отличие от трансверсальной изотропии проявляется относительно сдвигов. Также выявлено, что разница в использовании предложенного и традиционного определения эффективных свойств проявляется прежде всего при определении сдвиговых параметров потенциала. Выявлено, что в диапазоне деформаций до 20 % ортотропные потенциалы, построенные на основе потенциалов Трелоа-ра и Муни, приводят к близким результатам.
Определяющее соотношение эффективного гиперупругого материала может быть представлено в дифференциальном виде д2Weff (C)
d S =---- —d E .
d E 2
Это соотношение гиперупругого материала. В случае процесса нагрузки оно фактически используется в виде соотношения гипоупругого материала dS = CE (E): dE. (3)
Это соотношение предназначено для использования при формулировке задачи в начальной области. Для рези- e d 2WR eE d We ны C =---— , для резинокорда C =----—. В пред- dE2 dE2
положении физической линейности резинокордного материала C E = C E (0) = const. Соотношение (3) удобно использовать в конечно-элементной модели, поскольку оно является более общим по сравнению с соотношением гиперупругого материала (1).
При решении задачи в текущей области последнее соотношение эквивалентно определяющему соотношению
T TR = C d ( E ) : d , C d, = J -1 F ,p F jq F kr F s CE p4„ .
Здесь T TR – производная Трусделла [16] тензора напряжений Коши T , d – тензор скоростей деформации d ( w ) = 0,5 1 ( V w ) T + V w
4. Экспериментальное определение свойств вязкоупругости
Модели вязкоупругости [34] при больших деформациях встречаются в большом количестве работ. Это касается также обобщенной модели Максвелла в применении к резине и резинокорду (см., например, [7, 35–37]). В работах [36, 37] построены модели резинокорда. Отметим, что использование в анизотропном потенциале «изотропной» части также применялось в работах [34–36]. Впрочем, и других.
В данной работе рассматривается квазистатическое нагружение. В исследовании [38] взаимодействие меж- ду резиновой матрицей и кордом учитывалось при построении упругой потенциальной энергии. Тем не менее возникает вопрос, насколько сильно проявляется зависимость от скорости деформирования в случае нагружения, которое принято считать статическим. Для выяснения этого вопроса были проведены опыты по одноосному растяжению брекерной резины до деформаций 10 %. Опыты проведены в НИИ Механики МГУ на машине ZWICK.
Обнаружено, что резиновая смесь обладает существенными вязкоупругими свойствами. На рис. 3 показаны результаты одноосных опытов на растяжение – сжатие образца резины, применяемой в брекерном слое. Цифрой 1 обозначена диаграмма напряжение – деформация для скорости деформации примерно 10 - 5c - 1, цифрой 2 - диаграмма для скорости 10-4c - 1, а цифрой 3 - для скорости 10 - 2c - 1.
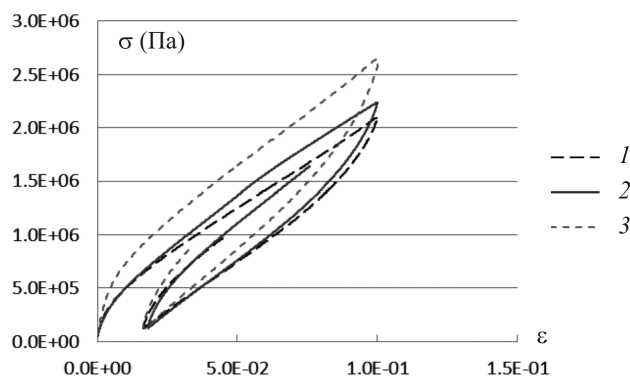
Рис. 3. График зависимости одноосного напряжения от инженерной деформации при растяжении слоя из брекерной резины при постоянной скорости нагружения
Fig. 3. Plot of uniaxial stress versus engineering strain under tension of a rubber ply at a constant loading rate
Опыты проводились с постоянной по величине скоростью деформации, изменяющейся скачком в начале опыта и при переходе от нагрузки к разгрузке и наоборот. Хорошо заметно проявление эффекта Малинза и наличие петли гистерезиса даже при скорости деформации 10 - 5 c - 1.
Проявление вязкоупругости также отчетливо видно при смене нагрузки и разгрузки. Следовательно, при медленном квазистатическом нагружении 10 - 5 ^ 10 - 4c - 1 тангенциальный модуль зависит от скорости деформации. На начальном участке деформирования он меняется после скачкообразного изменения скорости деформации.
Наличие петли гистерезиса даже для малых скоростей деформации говорит о том, что стандартное применение удобной модели вязкоупругости Максвелла следует понимать следующим образом. Обобщенная модель Максвелла, записанная относительно девиаторов s, e напряжений и деформаций t N^ f t )
s ( t ) = J R sh ( t - T): d e (T) » R sh = c « + L c n exP I -“I ,
0 n = 1 V t n )
подразумевает знание длительного модуля c ю . Вместо его измерения определяющее соотношение можно переписать в виде
t s (e) = sref (e) + j R (t — т)(е - eref) dт, где sref (e) есть определяющее соотношение напряжение – деформация при выбранной референсной скорости деформации. Предполагается, что эта зависимость определяется анизотропным упругим потенциалом, для построения которого разработана отмеченная выше методика. Таким образом, зная рефренную зависимость напряжения от деформации, можно вычислить аналогичную зависимость для актуальной скорости деформирования.
Проверка данного предположения проводилась в одноосном опыте до деформаций 10 %. Использовались опыты с тремя скоростями деформаций V 1 = 10 - 5 , V 2 = 10 - 4 и V 3 = 10 - 2. Предыдущая формула приобретает вид
— t
G a (e) — a , (e) = ( V , — V > 2 C „ t „ (1 — e" ), a = 2,3.
n
Параметры модели Максвелла при n = 2 выбирались методом наименьших квадратов из сравнения кривых oa(e) для a = 1,3. Аппроксимация для 0 2 (e) показана на рис. 4.
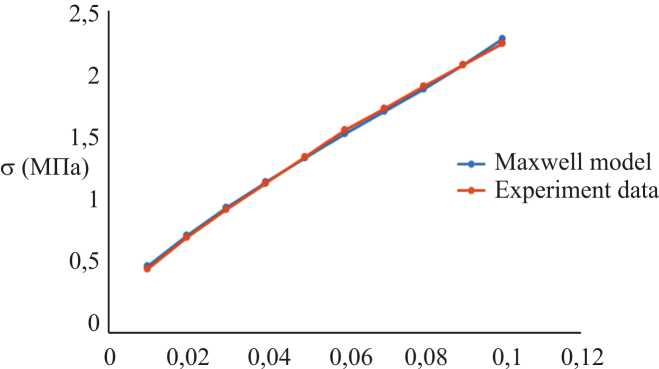
Рис. 4. График зависимости одноосного напряжения от инженерной деформации при растяжении резинового слоя при постоянной скорости деформация
Fig. 4. Plot of uniaxial stress versus engineering strain under tension of a rubber ply at a constant loading rate
Из рис. 4 видно, что кривая второго теста, рассчитанная по модели Максвелла, совпадают с данными эксперимента. Таким образом, проверено, что диаграммы о ~ е квазистатического нагружения до 10 % деформации могут быть получены из выбранной референсной кривой нагружения, используя линейную модель Максвелла.
j ( V w :[ F • C E • F T ]: V d u T +
V 0
+ S ( u ):[ V w •V d u T ] ) dV 0 = dA e ( w ).
так и текущей конфигурации j d(w): Cd • d(du)dV + j T :[Vw •VduT ]dV = dAe (w), VV где
dAe
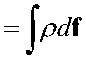
• w dV +
V Σ2
j d s • w dL
есть работа внешних
сил на приращениях внешних сил d f и d s . В первом случае подход называется полностью Лагранжевым (TL), перемещение u зависит от координат в начальной области и времени (или параметра прослеживания процесса t ). Во втором случае – это Лагранжев подход с адаптацией (UL) [3]. Нелинейный функционал dAe ( w ) сформулирован в текущей области, поскольку внутреннее давление является следящей нагрузкой и естественным образом формулируется в текущей области (текущей конфигурации). Объемная сила может представлять собой центробежную силу, или Кориолисову силу, если рассматривается вращение, а поверхностные силы - это внутреннее давление s = — p ( t ) n или силы в зоне контакта с дорогой.
Отметим, что разница между обеими формулировками отсутствует, если используются изопараметриче-ские элементы и не применяется перестроение сетки. Более того, оказывается, что при применении МКЭ некоторые интегралы удобно вычислять по исходной области, например, в случае гиперупругого материала, а другие в текущей области. Например, работу давления.
Линеаризованное вариационное уравнение было дискретизировано с помощью элементов первого порядка. Для интегрирования по времени используется неявный метод Эйлера с внутренними итерациями на каждом шаге. Число этих итераций невелико. Весь алгоритм реализован в виде программы на Фортране. Реализовано вычисление напряжений в корде, представляющих интерес в смысле прочности шины.
6. Численные примеры
Осуществлена детальная проверка разработанной программы. Ниже приводятся некоторые сравнения. Рассмотрим тест на одноосное растяжение пластины из линейно упругого материала, имеющего определяющее соотношение S = C : E . Решение в этой задаче дается формулой
5. Постановка квазистатической задачи
„ (1 + e/2)(1 + e) l — L о = E e—---------- —, e =---- .
(1 — 2ve(1 + e/2)) L
Вариационное уравнение квазистатической геометрически нелинейной задачи может быть сформулировано [39] как в начальной
Сравнение напряжений, полученных в собственной конечно-элементной программе, с этой формулой приведено ниже в табл. 1.
Таблица 1
Напряжение в задаче одноосного растяжения (МПа)
Table 1
Stress in the problem of uniaxial tension (MPa)
|
ε |
Формула |
Расчет |
Error (%) |
|
0,1 |
19 484 |
19 900 |
2,13 |
|
0,2 |
48 489 |
49 0000 |
1,05 |
|
0,3 |
91 175 |
88 500 |
2,9 |
Таблица 2
Сравнение прогибов
Table 2
Comparison of deflections
|
h / L |
Мат |
Гр. усл. |
Давление (МПа) |
ANSYS |
ABAQUS |
J |
diff ANS |
AB vs ANS |
|
0,1 |
R |
3 |
2,00E-05 |
0,849 |
0,884 |
0,838 |
1,30 % |
3,96 % |
|
1 |
R |
2 |
1,00E-03 |
2,48 |
2,59 |
2,41 |
2,82 % |
4,25 % |
|
0,1 |
M |
2 |
1,00E-01 |
0,302 |
0,302 |
0,299 |
0,99 % |
0,00 % |
|
2 |
R |
3 |
8,00E-03 |
2,022 |
2,33 |
1,966 |
2,77 % |
13,22 % |
|
0,1 |
M |
3 |
1,60E+00 |
0,678 |
0,68 |
0,673 |
0,74 % |
0,29 % |
|
1 |
R |
1 |
2,00E-03 |
6,21 |
6,39 |
5,98 |
3,70 % |
2,82 % |
|
2 |
M |
3 |
5,00E+02 |
1,42 |
1,43 |
1,41 |
0,70 % |
0,70 % |
Следующий тест – решение той же задачи, но для материала с определяющим соотношением о J = C: d, (4)
где σ J – производная Яуманна. Решение дается формулой о = E ln(1 + e). Численное решение почти точно совпало как с формулой, так и численными решениями, полученными в ANSYS и ABAQUS.
Следующие тесты – это цилиндрический изгиб пластинок из материала резины или металла. Расчеты проведены для параметров материала: для металла E = 1,6 - 10 5 МПа, v = 0,33, для резины E = 1,04 МПа, v = 0,49. Сравнение прогибов в центральном сечении приведено в табл. 2. Первый столбец таблицы показывает толщину пластины в мм, второй столбец указывает материал: «R» – резина, «М» – металл. В третьем столбце указаны граничные условия. Цифра 1 означает шарнирные опоры со свободным перемещением вдоль оси, 2 – такие же опоры, но с запретом продольного перемещения, цифра 3 означает заделку с обеих сторон. Четвертый столбец содержит величину давления в МПа. Далее три столбца содержат прогибы в среднем сечении полученные, соответственно, в Ансисе, Абакусе и собственной программе. Везде использовано определяющее соотношение (4) и одинаковые элементы типа Brick. Последние два столбца означают относительную разницу прогибов, полученных, в собственной программе и Ансис и разницу между Ансис и Абакус. Приведенные данные показывают лишь небольшую часть результатов тестирования собственной программы.
Основной вывод, который следует из результатов тестирования, состоит в том, что собственная программа обеспечивает точность такую же, как упомянутые выше программные комплексы. При этом разница в решениях между Ансис и Абакус такая же, как между ними и решением в собственной программе.
Геометрическая модель шины выбрана достаточно детальной, отражающей все основные элементы конструкции. На рис. 5 показана форма деформированной шины в конце процесса внедрения индентера.
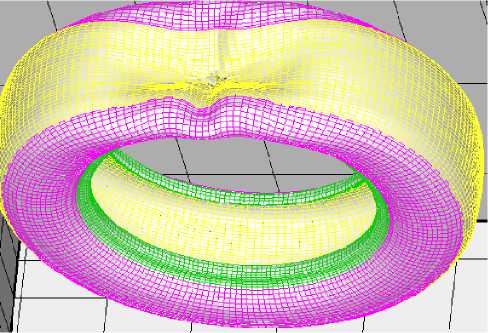
Рис. 5. Форма деформированной шины в конце процесса внедрения индентера
Fig. 5. The shape of the deformed tire at the end of the indentation process
Можно заметить явное сходство формы деформирования в модели с формой, показанной на рис. 1. Следует отметить, что шина чувствительна к деталям механической модели. Неточности в последней приводят к существенному изменению приведенной формы. На приведенном рисунке можно заметить отсутствие симметрии относительно центрального меридионального сечения под ин-дентером. Это вызвано тем, что два слоя брекера отстоят друг от друга на небольшое расстояние около 1 мм.
Заключение
Разработаны модели резинокордного слоя трансверсально-изотропного или ортотропного гиперупругого материалов. На основе модифицированного определения эффективных свойств выявлены параметры потенциалов как для слоев брекера, так и слоя каркаса. Сформулирована вариационная постановка квазистати-ческой задачи медленного нагружения шины и осуществлена ее конечно-элементная дискретизация. Последняя в свою очередь реализована в виде собственной программы на Фортране. Проведены проверочные тесты путем сравнения с аналитическими решениями и известными конечно-элементными программами. Реализовано моделирование теста на разрыв, являющегося в ряде стран обязательным.
Таким образом, разработанное моделирование НДС шины детально проверено как с точки зрения механической модели, так и вычислительной процедуры. Оно позволяет виртуально создавать прототипы новых конструкций шин и может быть полезно в шинной промышленности.
Список литературы Моделирование резинокордных слоев при квазистатическом нагружении
- Бухин Б.Л. Введение в механику пневматических шин. - М.: Химия, 1988. - 222 с.
- Böhm F. Zur Mechanik des Luftreifens. Habilitationsschrift. - TH Stuttgart, 1966.
- Bathe K. Finite element procedures. - 2nd ed. - Watertown, MA, 2014. -1065 p.
- Белкин А.Е. Разработка системы моделей и методов расчета напряженно-деформированного и теплового состояний автомобильных радиальных шин: дис. … д-ра техн. наук. - М.: МГТУ им. Н.Э. Баумана, 1998. - 284 с.
- Zur inneren Mechanik des Radialreifens. Teil 2.: Geschichtete Kompositschale mit diskreten Verschiebungsansatzen fur die einzelnen Schichten / G.M. Kulikov, F. Bohm, A. Duda, R. Wille, S.V. Plotnikova // Technische Mechanik. - 2000. - Bd. 20, n. 1. - P. 81-90.
- On the finite element solution of the threedimensional tire contact problem / H. Rothert, H. Idelberger, W. Jacobi, G. Laging // Nuclear Engineering and Design. - 1984. - Vol. 78, № 3. - P. 363-375.
- An efficient viscoelastic formulation for steady-state rolling structures / H. Rothert, L. Nasdala, M. Kaliske, A. Becker // Computational Mechanics. - 1998. - № 22. - P. 395-403.
- Feng K. Statische Berechnung des G¨urtelreifens unter besonderer Ber¨ucksichtigung der kordverst¨arkten Lagen // Fortschrittberichte VDI, Reihe 12, Nr. 258. - TU, Berlin: VDI Verlag, 1995. - 150 p.
- Победря Б.Е., Шешенин С.В. Трехмерное моделирование напряженно-деформированного состояния пневматических шин // Проблемы шин и резинокордных композитов: труды 8-го Международного симпозиума. - М.: НИИШП, 1997. - Т. 2. - С. 320-326.
- Маргарян С.А. Численное моделирование напряженно-деформированного состояния пневматических шин: дис. … канд. физ.-мат. наук. - М.: МГУ, 2000.
- Sheshenin S.V., Margarjan S.A. Tire 3D numerical simulation // International Journal for Computational Civil and Structural Engineering. - 2005. - Vol. 1. - P. 33-42.
- Шешенин С.В. Трехмерное моделирование шины // Изв. РАН. Механика твердого тела. - 2007. - № 3. - С. 13-21.
- Соколов С.Л., Ненахов А.Б. Применение метода конечных элементов к решению задачи о нагружении радиальных шин локальной нагрузкой // Проблемы шин и резинокордных композитов. Математические методы в механике, конструировании и технологии: сборник трудов VI Симпозиума. - М.: НИИШП, 1995. - С. 239-243.
- Шешенин С.В., Бахметьев С.Г. Модель эффективного слоя для резинокордного материала // Вестник МГУ. Сер. 1. Математика. Механика. - 2014. - № 5. - С. 41-45.
- Шешенин С.В., Ду Икунь. Модель резинокорда при умеренно больших деформациях // Механика композиционных материалов и конструкций, сложных и гетерогенных сред: Сборник трудов 8-й Всероссийской научной конференции с международным участием им. И.Ф. Образцова и Ю.Г. Яновского. - М.: ООО «Сам Полиграфист», 2019. - С. 101-109.
- Bonet J., Wood R.D. Nonlinear continuum mechanics for finite element analysis. - New York: Cambridge University Press, 2008. - 340 p.
- Победря Б.Е. Лекции по тензорному анализу. - М.: Изд-во Моск. ун-та, 1974. - 206 с.
- Hill R. Elastic properties of reinforced solids: some theoretical principles // Journal of the Mechanics and Physics of Solids. - 1963. - Vol. 11. - P. 357-372.
- Hill R. A self-consistent mechanics of composite materials // Journal of the Mechanics and Physics of Solids. - 1965. - Vol. 13. - P. 213-222.
- Hashin Z. Analysis of composite materials // Journal of Applied Mechanics. - 1983. - Vol. 50, № 3. - P. 481-505.
- Победря Б.Е. Механики композиционных материалов. - М.: Изд-во Моск. ун-та, 1984. - 336 с.
- Шешенин С.В., Ду Икунь. Гомогенизация резинокордного слоя при умеренно больших деформациях // Механика композитных материалов. - 2021. - Т. 57, № 3. - С. 395-410.
- Bensoussan A., Lions J.-L., Papanicolaou G. Asymptotic analysis for periodic structures. - Amsterdam, New York: North-Holland Pub. Co., 1978. - 392 p.
- Sanchez-Palencia E. Non-homogenous media and vibration theory (Lecture Notes in Physics). - New York: Springer-Verlag, 1980. - 400 p.
- Бахвалов Н.С., Панасенко Г.П. Осреднение процессов в периодических средах. - М.: Наука, 1984. - 352 с.
- Kohn R.V., Vogelius M. A new model of thin plates with rapidly varying thickness // International Journal of Solids and Structures. - 1984. - Vol. 20. - P. 333-350.
- Levinski T., Telega J.J. Plates, laminates and shells: asymptotic analysis and homogenization. - New York: World Scientific Pub. Co., 2000. - 739 p.
- Pidaparti R., Kakarla V. Three-dimensional stress analysis of two-ply cord-rubber composite laminates // Composite Structures. - 1994. - Vol. 28. - P. 433-440.
- Pidaparti R., May A. A micromechanical analysis to predict the cord-rubber composite properties // Composite Structures. - 1996. - Vol. 34. - P. 361-396.
- Jones R.M. Mechanics of Composite Materials. - Philadelphia: Taylor & Francis, 1998. - 519 p.
- Шешенин С.В. Асимптотический анализ периодических в плане пластин // Изв. РАН. Механика твердого тела. - 2006. - № 6. - С. 71-79.
- Шешенин С.В, Ду Икунь. Две модели резинокордного слоя // Механика композиционных материалов и конструкций. - 2021. - Т. 27, № 2. - С. 191-204.
- Дудников В.А., Назаров С.А. Асимптотически точные уравнения теории тонких пластин на основе теории Коссера // Докл. АН СССР. - 1982. - Т. 262, № 2.- С. 306-309.
- Методы прикладной вязкоупругости / А.А. Адамов, В.П. Матвеенко, Н.А. Труфанов, И.Н. Шардаков. - Екатеринбург: УрО РАН, 2003. - 411 с.
- Marvalova B. Viscoelastic properties of filled rubber. Experimental observations and material modeling // Engineering Mechanics. - 2007. - Vol. 14, № 1/2. - P. 81-89.
- Nam T.H. Mechanical properties of the composite material with elastomeric matrix reinforced by textile cords. PhD thesis. - Liberec: Technical University of Liberec, 2004. - 130 p.
- Tuan H.S., Marvalova B. Constitutive material model of fiber-reinforced composites at finite strains in comsol multiphysics // 15th annual conference proceedings. Conference Technical Computing. - Prague, 2007.
- Zihan Zhao, Xihui Mu, Fengpo Du. Constitutive model research for rubber-cord composites used in rubber track // Materials Today Communications. - 2020. - Vol. 23. doi: 10.1016/j.mtcomm.2020.100937
- Bonet J., Wood R.D. Nonlinear continuum mechanics for finite element analysis. - New York: Cambridge University Press, 2008. - 340 p.


