Моделирование резонансной фокусировки пикосекундного и фемтосекундного импульсов диэлектрическим микроцилиндром

В последнее время много внимания уделяется изучению субволновой фокусировки лазерного света на микрочастицах, в том числе на микросферах и микроцилиндрах, радиусы которых сравнимы с длиной волны света [1–5]. Так, в [1–4] численно изучалась фокусировка многослойными микросферами [1], сфероидальными микросферами [2] и двухслойными микросферами [3, 4]. При этом минимальный диаметр фокусного пятна по полуспаду интенсивности был равен FWHM=0,4λ [2], а максимальная глубина фокуса равна DOF=20λ [3] и DOF=22λ [4]. В [5, 6] рассматривалась фокусировка микроцилиндром: эллиптическим [5] и многослойным [6]. Минимальный размер фокуса был получен FWHM=0,46λ [6]. В [7, 8] моделировалась резонансная фокусировка света микросферами. В [7] с помощью диэлектрической микросферы вместе с нанометровым металлическим шариком получена резонансная фокусировка света в пятно с диаметром FWHM=0,25λ, а для диэлектрической микросферы получен резонансный фокус размером FWHM=0,40λ [8]. В [9] аналитически с помощью ряда из функций Бесселя рассматривалась резонансная фокусировка ТЕ-поляризованного лазерного света микроцилиндром из полиэстра (показатель преломления n = 1,59). Для 18-й моды (мода шепчущей галереи) получен фокус вне микроцилиндра размером FWHM=0,22λ.

В данной работе с помощью FDTD-метода исследуется фокусировка ТЕ-поляризованных пико- и фемтосекундных импульсов на диэлектрическом микроцилиндре с резонансным радиусом. После прохождения импульса в цилиндре остаётся вытекающая мода шепчущей галереи (для пикосекундного импульса). Для 18-й моды насыщение наступает после прохождения 1200 периодов (2,5 пс), а для 19 – после прохождения 3500 периодов (7,3 пс). При распространении фемтосекундного лазерного импульса длительностью 17,08 фс через диэлектрический цилиндр с коэффициентом преломления 1,59 и резонансным радиусом 0,7152 длины волны (5 мода) ширина фокусного пятна по полуспаду интенсивности равна 0,235 центральной длины волны. При этом мода внутри цилиндра не успевает сформироваться.

• 1.    Фокусировка пикосекундного импульса

  Рассмотрим моделирование распространения плоской ТЕ-волны через цилиндр в течение 2,5 пс и 7,3 пс. Моделирование проводится с помощью решения уравнений Максвелла FDTD-методом, реализованным в FullWAVE. Параметры моделирования: длина волны излучения λ = 0,633 мкм, радиус цилиндра R = 2,1749λ, показатель преломления среды 1, показатель преломления цилиндра n = 1,59. Шаги дискретизации по пространственным переменным – 0,002 мкм, по времени – 0,0001 мкм.

• 2.    Фокусировка фемтосекундного импульса

На рис. 1 приведены графики максимальной интенсивности, по которым можно оценить количество периодов в излучении, после прохождения которых процесс выйдет на насыщение. Из рис. 1 видно, что для 18й моды насыщение (когда наступает стационарная ситуация: накопленная в цилиндре в единицу времени энергия становится равна вытекающей из цилиндра энергии) наступает после прохождения 1200 периодов (2,5 пс), а для 19-й – после прохождения 3500 периодов (7,3 пс).

На рис. 2 показано распределение интенсивности внутри цилиндра в момент прохождения 1000 периодов импульса длительностью 2,5 пс через цилиндр радиуса R=2,1749λ. Ширина фокусного пятна (рис. 2) достигает наилучшего значения FWHM=0,22λ и совпадает с аналитически рассчитанным [9].

Промоделируем резонансную фокусировку диэлектрическим микроцилиндром фемтосекундных импульсов длительностью t s 17,08 фс и 8,54 фс. С помощью методов, изложенных в [10], возможно рассчитать резонансные радиусы цилиндров для пятой моды (табл. 1).

В статье были рассмотрены такие материалы, как полиэстр и кварцевое стекло (коэффициенты преломления соответственно 1,59 и 1,46). Моделирование проводилось в пакете FullWAVE. Шаги дискретизации по пространственным переменным – 0,002 мкм, по времени – 0,0001 мкм. Результаты моделирования приведены на рис. 3 а , б . В табл. 2, 3 приведены параметры фокусного пятна для рассмотренных случаев.

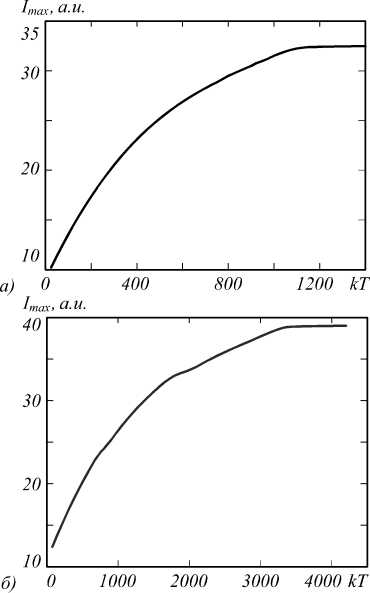
Рис. 1. Зависимость максимальной интенсивности в фокусе от длительности импульса (в периодах) для а) 18-й моды (R = 2,1749λ) ⋅ , б) 19-й моды (R = 2,284λ)

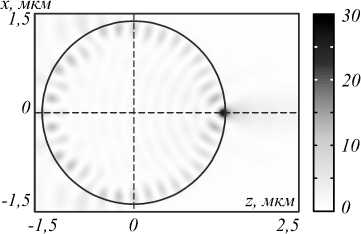
Рис. 2. Распределение интенсивности в ходе дифракции ТЕ-импульса света длительностью 2,5 пс (1200 периодов) на цилиндре (R = 2,1749 λ) в момент прохождения 1000 периодов

Табл. 1. Радиусы цилиндров

n	1,59	1,46	f(ω)
R, λ 0	0,7152	0,7588	0,7588
R , мкм	0,3802	0,4037	0,4037

Табл. 2. Параметры фокусного пятна для цилиндра из полиэстера (n = 1,59)

t s , фс	FWHM x , λ 0	DOF z , λ 0	Imax , a.u.
17,08	0,235	0,271	9,447
8,54	0,243	0,271	8.091

Табл. 3. Параметры фокусного пятна для цилиндра из кварцевого стекла (n = 1,46)

t s , фс	FWHM x , λ 0	DOF z , λ 0	Imax , a.u.
17,08	0,255	0,316	8,204
8,54	0,262	0,320	7,634

В работе [11] показано, что в случае моделирования фемтосекундных импульсов необходимо учитывать зависимость диэлектрической проницаемости от частоты. Воспользуемся моделью Селлмейера для кварцевого стекла [12] и проведём моделирование с помощью (FD)²TD метода, реализованного в пакете FullWAVE, на вышеприведённых параметрах. Результаты моделирования приведены на рис. 4 в . В табл. 4 приведены параметры фокусного пятна для рассмотренных случаев.

Табл. 4. Параметры фокусного пятна для цилиндра из кварцевого стекла (n = f(ω))

t s , фс	FWHM x , λ 0	DOF z , λ 0	Imax , a.u.
17,08	0,255	0,316	8,241
8,54	0,262	0,316	7,605

Из сравнения табл. 3 и табл.4 видно, что в данном случае учётом дисперсии вещества можно пренебречь , так как отклонение результатов составило менее 2%.

Из рис. 3 видно, что в цилиндре успевает сформироваться мода шепчущей галереи за время прохождения фемтосекундного импульса. Однако она достаточно быстро вытекает из него. Из табл. 2–4 и рис. 4 видно, что при резонансной фокусировке фемтосекундного импульса удаётся преодолеть дифракционный предел (0,44λ 0 /n = 0,28λ 0 для полиэстра и 0,44λ 0 /n=0,30λ 0 для кварца).

Рис. 3. Дифракционная картина резонансной фокусировки на цилиндре а) n = 1,59; б) n = f(ω); в) n = 1,46 для импульса длительностью 17,08 фс

Для сравнения было промоделировано распространение фемтосекундного импульса длительностью 17,08 фс через цилиндр из кварцевого стекла ( n = 1,46) с радиусом, отличным от резонансного

R=0,8λ0. Ширина фокусного пятна по полуспаду ин тенсивности составила 0,269λ0. Таким образом, изме нение радиуса цилиндра на 5 % влечёт за собой изме нение ширины фокусного пятна на 5 %.

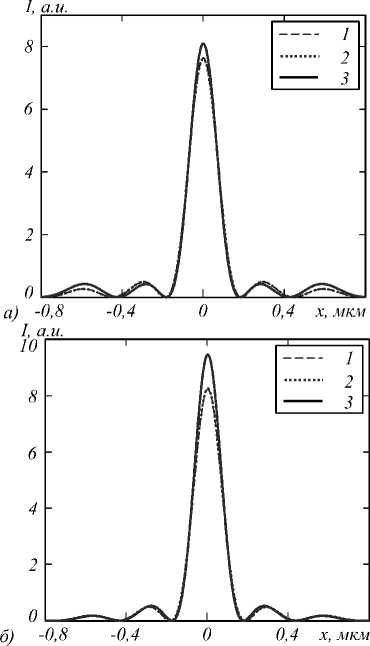
Рис. 4. Распределение интенсивности в фокусе для цилиндров с n = f(ω) – линия 1; n = 1,46 – линия 2; n = 1,59 – линия 3 для импульса длительностью: а) 8,54 фс, б) 17,08 фс

Это свидетельствует о том, что малая длительность импульса не даёт раскрыться резонансным эффектам, хотя разница в динамике фокусировки одного и того же импульса на двух цилиндрах с близкими радиусами заметна. На рис. 5 представлена динамика изменения интенсивности в фокусе. Время измеряется в количестве k пройденных импульсом периодов.

Из рис. 5 видно, что в случае выбора цилиндра с резонансным радиусом интенсивность в фокусе постоянно растёт (максимальная интенсивность в 8,2 раза превышает максимальную интенсивность падающего света), в то время как в случае с цилиндром нерезонансного радиуса значение быстро достигает своего максимума и с течением времени уже не меняется (максимальная интенсивность в 7,3 раза превышает максимальную интенсивность падающего света).

Заключение

В работе показано, что по мере прохождения пикосекундного импульса через цилиндр с коэффициентом преломления 1,59 ширина фокуса уменьшается, интенсивность в фокусе растёт, также растёт энергия моды, запасённая внутри цилиндра. Для 18-й моды насыщение (стационарный случай) наступает после прохождения 1200 периодов (2,5 пс), а для 19-й – после прохождения 3500 периодов (7,3 пс). Заметим, что для формирования следующей по номеру моды требуется увеличение длительности импульса почти в 2 раза. Ширина фокусного пятна, формируемого импульсом длительностью 2,5 пс, при прохождении через цилиндр радиуса R = 2,1749λ, достигает минимального значения FWHM=0,22λ и совпадает с аналитически рассчитанным в стационарном случае [8, 9]. При этом изменение радиуса цилиндра на 2% влечёт увеличение размера пятна на 32%.

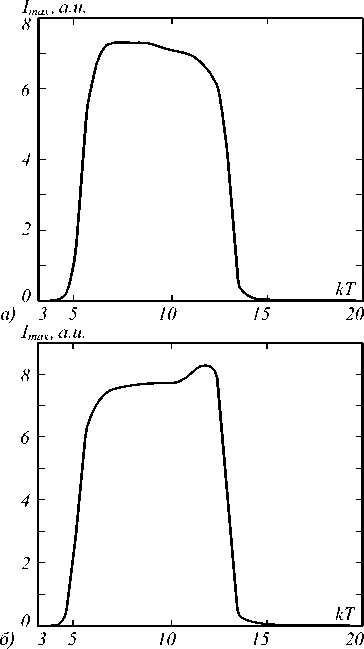
Рис. 5. Динамика изменения интенсивности в фокусе при прохождении импульса длительностью 17,08 фс через цилиндр с радиусом а) R = 0,8λ ₀ и б) R = 0,7588λ ₀

При распространении фемтосекундного лазерного импульса длительностью 17,08 фс через диэлектрический цилиндр с коэффициентом преломления n = 1,59 и радиуса R = 0,7152λ₀ (5 мода) ширина фокусного пятна по полуспаду интенсивности равна FWHM=0,235λ₀. Длительности импульса не хватает для формирования моды в цилиндре, и резонансные эффекты почти не проявляются. Так, изменение радиуса цилиндра на 5 % приводит к изменению ширины фокусного пятна на 5 %. Хотя разница в динамике формирования интенсивности в фокусе для цилиндров с резонансным и нерезонансным радиусами заметна.

Работа выполнена при поддержке Министерства образования и науки РФ, гранта Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9) и молодого учёного кандидата наук МК-4816.2014.2, а также грантов РФФИ 13-07-97008, 14-29-07133, 1407-31218 и 15-07-01174.