Моделирование рыночных манипуляций в реальном времени

Целью данной работы стала разработка приложения для моделирования рыночных манипуляций с участием реальных игроков. Такое развитие инструментария поспособствует исследованию проблемы экспериментальным путём. Для достижения результата, был разработан дизайн эксперимента, подобраны численные параметры, проведена, серия экспериментов, участниками которых были студенты МФТИ.

2.    Дизайн эксперимента

В данной работе на базе платформы оТгее [4] было создано веб-приложение для экспериментальных исследований одной из конфигураций манипулятивной схемы P&D в форме игры в непрерывном времени с участием реальных игроков. Приложение даёт каждому игроку возможность торговать на рынке, имитирующем реальную биржу, где представлены три различных инструмента: CUi, CU2, CU3. В зависимости от целей эксперимента и количества игроков исследователь имеет возможность изменять режим работы приложения: для исследования поведения только неосведомлённых о манипуляции масс, где роль организатора манипуляции выполняет само приложение; для исследования полностью замкнутого рынка, где сами игроки выполняют все роли; промежуточные гибридные режимы с разной степенью вмешательства программы в процесс изменения цены.

В модели приложения каждый инструмент CUi имеет свою начальную настройку из четырёх параметров:

р0, стг, const2, аг, где р0 ~ стартовая цена инструмента в условных единицах, и2 - показатель, отвечающий за волатильность, const2 и аг - параметры функционала, отвечающего за поведение цены инструмента. Для увеличения заинтересованности игроков и имитации влияния внешних факторов ценой каждого инструмента управляет винеровский процесс. С периодом Т цена инструмента меняется по формуле

Pt+T = Pt + Е2, где Ег ~ N(0, (стг)2Т).

Для получения искомого роста и падения цены у выбранного для манипуляции инструмента встроена зависимость цены от совершаемых игроками действий и ситуации на рынке. Такая функция не является прообразом ценообразования на реальных рынках, но имитирует реальные тенденции на небольшом временном промежутке, моделируемом в эксперименте [5]. Варьируя различные параметры функции, можно задать для конкретной модели инструмента требуемое поведение внутри эксперимента в зависимости от действий игроков. В общем случае все такие функции имеют вид

инструмент; взаимодействие внутри множества игроков, где все осведомлены о манипуляции.

3.    Результаты эксперимента

К моменту написания статьи были проведены три игровых сессии по 3-5 раундов, каждой сессии соответствует уникальный состав игроков. От раунда к раунду доля участников манипуляции варьировалась и принимала значения 50% или 100%, а в случае первого в сессии раунда - 0%. По завершении раунда приложение возвращает таблицу с данными обо всех операциях всего множества игроков с метками времени, на основании которой проводился весь дальнейший анализ.

Далее продемонстрированы результаты на примере одного раунда, в ходе которого манипулируемым инструментом был CU1, доля осведомлённых о манипуляции игроков равнялась 50%, Т = 5 секунд, где Т - период обновлений цены случайным процессом в (1). Начальный портфель игрока разделён поровну на четыре составляющих между тремя инструментами и удельными единицами и к началу игры эквивалентен 20 000 у.е. Параметры инструмента CU1 : ро = 100 у.е., у = 0.6, а = 1; параметр const в каждой сессии подбирался под а и количество игроков таким образом, чтобы управляющая функция (2) позволяла половине игроков, единовременно вложив полностью свои активы в инструмент, поднять его цену на ро • 60% у.е.

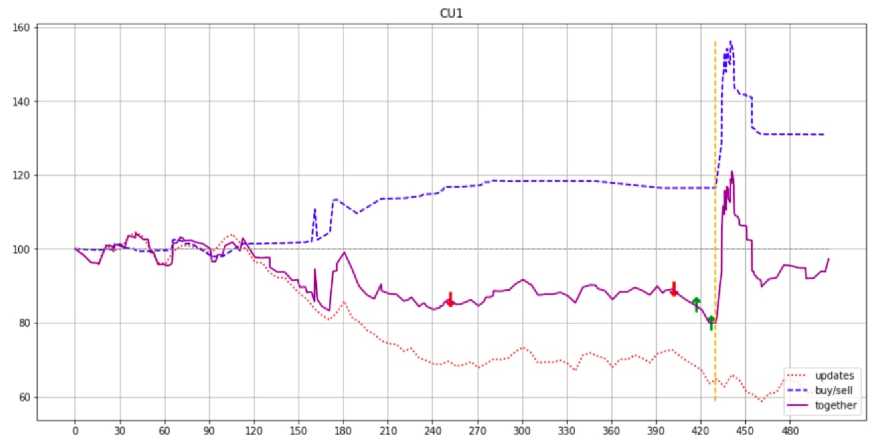
Рис. 1. Динамика цены CU 1 в разрезе влияния игроков и внешнего влияния

На рис. 1 представлена динамика цены инструмента CU1 (игра заняла чуть более восьми минут). Сплошной линией обозначена реальная хронология цены, пунктирной линией -влияние на цену только торговыми операциями со стороны игроков, точечной пунктирной линией - влияние на цену только обновлениями со стороны случайного процесса. Кроме этого, вертикальной чертой отмечен момент объявления о начале манипуляции. Стрелками, направленными вверх и вниз, отмечены новости, касающиеся инструмента CU1 и утверждаемый в них прогноз (стрелка вверх - прогноз на рост цены, стрелка вниз - прогноз на спад цены).

В ходе раунда удалось смоделировать в лабораторных условиях эффект от организованной манипуляции: цена инструмента с начала манипуляции за 10 секунд увеличилась с 80 у.е. до 120 у.е. (скачок на 40% от стартовой цены и на 50% от последней перед манипуляцией); затем последовал практически настолько же резкий спад цены вследствие массовой продажи инструмента.

На рис. 2 в верхней части представлена плотноств операций - среднее количество операций, совершаемых игроками в секунду, вычисленное в пределах временного окна. Яркая сплошная линия отображает плотноств, вычисленную в окне размером 15 секунд, бледная сплошная линия - пятв секунд, точечная пунктирная линия - три секунды. С помощвю данных графиков предлагается изучать влияние новостей на активность игроков. На некоторых участках раунда наблюдается явная реакция трейдеров на новости, на других - нет. В данном конкретном раунде активность игроков слабо отвечала новостям. Более того, инструментом CU1, позиционируемым как слабый и неустойчивый, в целом торговали мало: с учётом активного периода манипуляции, когда плотность доходила до 14-ти операций в секунду, с данным инструментом было совершено 225 операций покупки и продажи. Для сравнения, в нижней части рисунка аналогичный график для инструмента CU3, позиционируемого как наиболее сильный и устойчивый: было совершено 215 операций, интерес к инструменту имел гораздо более постоянный характер.

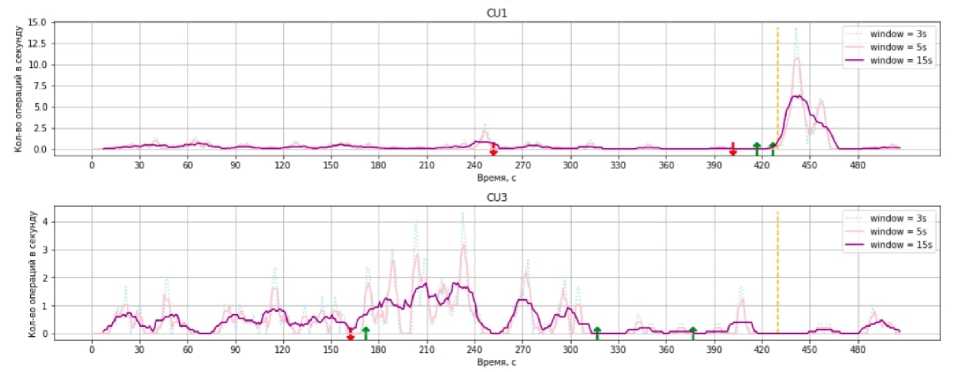
Рис. 2. Средняя плотность операций с монетами CU 1, CU 3 с размерами окна 3 с, 5 с, 15 с

На рис. 3 представлена динамика изменения цены инструмента CU1 под влиянием только операций игроков на отрезке 420-460 с. Каждая точка - операция по купле-продаже одним игроком; идущее вверх ребро изображает покупку инструмента, вниз - продажу. Пунктирные красные линии иллюстрируют операции, совершённые игроками, участвовавшими в манипуляции; сплошные синие линии - игроками, не осведомлёнными о манипуляции. Одним из качественных достижений эксперимента является крупная покупка инструмента CU1 игроком, не осведомлённым о манипуляции, в самом разгаре «накачивания» инструмента. Одним присутствием этой крупной покупки подтверждается, что лабораторный процесс не просто имел схожую с реальной форму графика цены инструмента, но и по смыслу подражает реальным манипуляциям: совершивший искомую покупку игрок не имел представления о сговоре, действовал только на основании новостей и динамики цены инструмента.

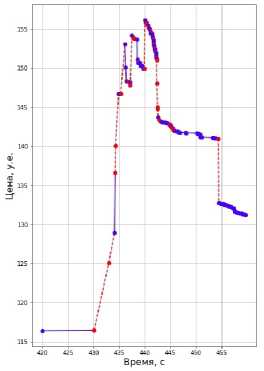
Рис. 3. Формирование пика, операциями участвовавших игроков (красная пунктирная линия) и пеучаствовав-ших (синяя сплошная)

4.    Обнаружение аномалий

К полученным в ходе эксперимента данным был применён метод обнаружения манипуляций, предложенный в [6]. Данные о динамике цены инструмента преобразуются в формат диаграммы OHLC; здесь же появляется первый гиперпараметр будущей модели т - длительность одной свечи. На преобразованных данных происходит разрезание их на кадры - объединения нескольких идущих подряд свечей; количество свечей в кадре N - второй гиперпараметр модели. Результатом этих преобразований является набор кадров - точек в многомерном пространстве. На этом множестве применяется метод понижения размерности для последующего отображения их на плоскость (в оригинальной статье [6] использовался метод главных компонент, однако в данной работе кроме него были опробованы t-SNE и MDS). На множестве двумерных точек применяются методы расстояния и плотности для обнаружения аномалий; найденная моделью аномальная точка (кадр) расценивается как участок временного ряда, содержащий аномальную динамику цены.

Метрикой качества моделей была выбрана расширенная Ғ-мера с коэффициентом /3 = 2 (полнота модели важнее точности):

(1 + (^Precision • Recall

³     з 2Precision + Recall

Ориентируясь на Ғ-меру по сетке были подобраны оптимальные гиперпараметры среди обеспечивающих длину кадра от 10 до 40 секунд.

На рис. 4 продемонстрирован результат отображения на плоскость данных о динамике цены инструмента CU1 в 13-ти раундах методом главных компонент с гиперпараметрами т = 4, N = 5. Вычисление метрик Precision и Recall учитывало, что для выполнения задачи модели необходимо найти хотя бы один из серии идущих подряд кадров, содержащих этапы манипуляции. Полнота модели в данном случае составила 1.

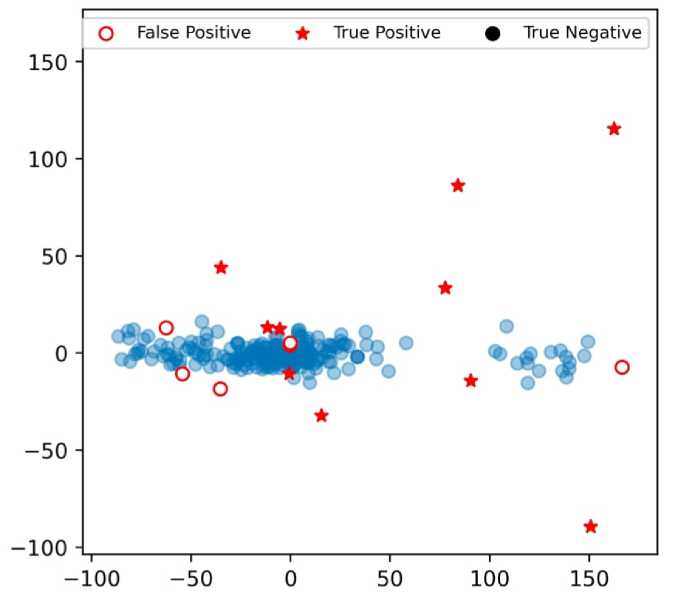
Рис. 4. Отображённое на. двумерную плоскость множество кадров

На рис. 5 проиллюстрирована разметка графика цены инструмента CU1 в раунде, продемонстрированном в разделе 3. Из трёх кадров, которые были изначально размечены как манипуляции, модель сработала на двух (кадры выделены жёлтым цветом), пропуск третьего кадра в таком случае ошибкой не считался (выделен серым цветом). Также модель допустила одно ложное срабатывание на кадре в первой половине раунда (выделен голубым цветом). Все три срабатывания модели в этом раунде обусловлены методом плотности.

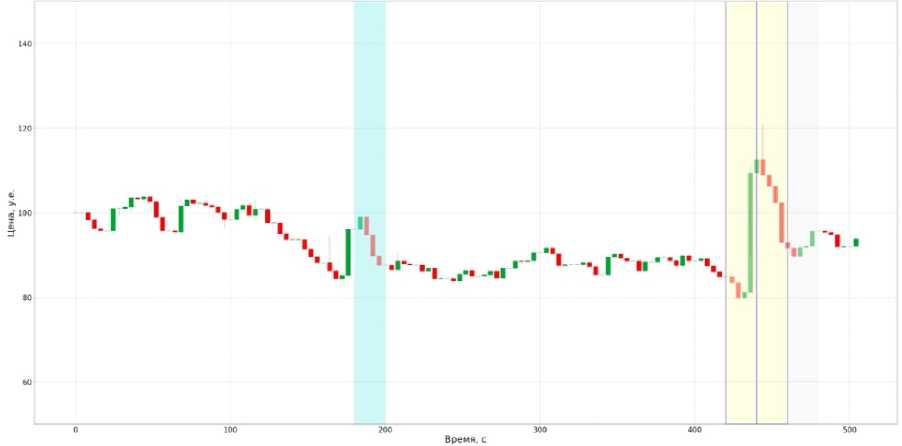
Рис. 5. Разметка, кадров моделью в раунде, отображённом на. рис. 1

В итоге расширенная Ғ-мера для метода главных компонент при оптимальных гиперпараметрах принимает значение 0,54 при полноте модели 0,77.

5.    Заключение

Описанное приложение удачно совмещается с функционалом предложенных ранее моделей [6], что было прямо продемонстрировано в данной работе. Приложение даёт возможность исследователям получать статистические данные в зависимости от установленных настроек для последующего анализа, имеющимися инструментами [7]. Одним из ключевых преимуществ в работе с приложением являются возможность обучения моделей с учителем и возможность их точной оценки - в работе с реальными данными сложнее оценивать качество работы моделей, так как достоверно неизвестен факт наличия или отсутствия манипуляции на. конкретном промежутке времени. Кроме упомянутых выше возможностей, с появлением данного приложения появляется большое пространство для исследования влияния психологической составляющей игроков на. результаты для исследования конфигураций новостного пространства, и его связи с распределением плотности операций во времени.