Моделирование самоподобного трафика
Автор: Привалов А.Ю., Баева М.В.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Управление и моделирование
Статья в выпуске: 4 т.8, 2006 года.
Бесплатный доступ
Предложен метод иммитационного моделирования сетевого телекоммуникационного трафика, обладающего самоподобными свойствами. Для генерируемого трафика может быть задан параметр Херста, характеризующий самоподобные свойства и однмерное распределение вероятностей.
Короткий адрес: https://sciup.org/148197868
IDR: 148197868 | УДК: 519
Текст научной статьи Моделирование самоподобного трафика
Целью статьи является исследование одного из возможных подходов к моделированию самоподобного трафика в сетях передачи данных. Поскольку самоподобная природа сетевого трафика затрудняет его анализ и моделирование классическими методами, последнее десятилетие специалисты уделяли большое внимание разработке новых моделей, подходов и методов решения такого рода задач. На сегодняшний день получен ряд важных и интересных результатов в этой области (см., например, [1-3]), некоторые из которых послужили отправной точкой данной работы.
Одним из популярных способов моделирования трафика, обладающего заданными самоподобными свойствами, является использование модели ”Input M/G/ z ”. Поскольку русская терминология в данной области ещё не сформировалась, будем использовать пословный перевод, и называть ее “моделью типа входная M/G/ҐҐ”. Популярность этой модели обусловлена рядом её достоинств. Во-первых, она относительно проста и ее легко использовать для генерации искусственных трасс трафика произвольной длины, во-вторых она дает простое физическое обоснование cамоподобных свойств трафика (такое, например, как наличие долговременных зависимостей и т.д.).
В данной работе мы рассмотрим один из возможных подходов к моделированию самоподобного трафика с заданными статистическими характеристиками с использованием модели “входная M/G/ҐҐ”.
Основные определения
В дальнейшем изложении нам понадобятся определение самоподобия и достаточное условие самоподобия в широком смысле. В данном параграфе мы приведём необходимые определения, а также подробное описание исходной модели “входная M/G/ҐҐ”.
Пусть X = { Xt } = (..., X 1 , X 2 ,...) стационарный в широком смысле случайный процесс дискретного времени, t е I _= {...., - 1,0,1,...}.
Пусть ц = EXt < z , xt = Xt - ц (центрированный процесс), дисперсия и автокорреляционная функция процессов X и x есть:
var
X
,
=
var
xt
=
о
2
=
Ext
2
E ( .x t x t + k )
rX ( k ) ,2 , (2)
σ X
µ,σX ,rX (k) не зависят от t вследствие ста ционарности Xt и xt .
Пусть
X t* m ) = -( X „ - m . 1 + ... + X „ ),t е I ,. (3) m 1
Процесс X ( m ) = (..., X 1 ( m ) , X 2 m ) ,...)- стационарный в широком смысле случайный процесс с дискретным временем, обозначим через rX ( m ) ( k ) автокорреляционную функцию процесса X t ( m ) .
Определение 1: Процесс X называется асимптотически самоподобным второго порядка с параметром Херста H = 1 - в / 2 ,
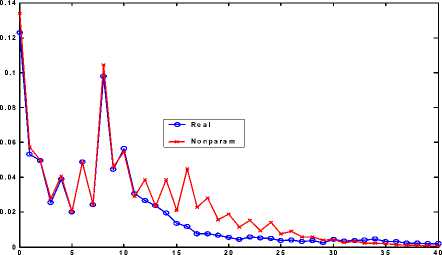
0 Свойство: (доказано в [1]) Если lim rXm)(k)/ k -e = const тогда m ^да 1) lim var X(m) / m-e = const• 7 m ^да’ 2) lim rXm)(k) = g(k), k e i(5) 7 m^да 1 Именно асимптотическое самоподобие второго порядка мы исследуем в данной работе, и далее будем называть его просто самоподобием. Опишем модель трафика “входная M/G/ ҐҐ”, обладающую самоподобными свойствами. Пусть имеется некоторый пуассоновский процесс с интенсивностью X, и пусть At - количество пуассоновских событий в интервале [t, t +1), t е I-да. Обозначим через A = (...A-1, A0, A1,...) последовательность независимых одинаково распределённых случайных величин At с пуассоновским законом распределения Pr{At = k} = e-XX k / k!. Пред- положим, что At – количество новых активных источников информационного трафика, появившихся в некоторой сети связи во временном окне t. Каждый такой источник имеет период активности в сети, после окончания которого он исчезает. Длина периода активности (“время жизни в сети”) источника i, возникшего во временном окне t (i=1,2,…At ) – это случайная величина Tt,i е 11. Кроме того, каждый источник имеет свою скорость генерации информации в течение активного периода (измеряемую в условных единицах, называемых ячейками), которая описывается как случайный процесс St,i (n) , где n – время от начала этого перио да, St,i (n) е 10, n е 10. Пусть случайные пары (τt,i , St,i(n)) независимы, одинаково распределены и не зависят A. Определим сетевой трафик как случайный процесс Y = (...,Y-1, Y0, Y1,...), tt Y= X X Sk (tt - k)I(тк •> t - k), t k,i k,i k = -да г = 1 (6) где I(.) индикатор события: 1, если т, . > t - k k, г 1(тк ,i> t -k)=i 0, иначе , то есть значение случайного процесса Yt в момент времени t является суммарной интенсивностью генерации ячеек от всех активных источников. Если EYt< да, то процесс Yt стационарный и эргодический. Одним из самых простых, и в тоже время интересных для практики случаев является случай постоянной скорости, одинаковой для всех источников, когда St,i (n) = R = const, а времена жизни источников являются независимыми одинаково распределёнными случайными величинами. Теорема: (доказана в [1] ). Если для указанного выше частного случая для распределения времени жизни источника выполняется условие const lim Рг{т > n} =----- m ^да na , 1<a<2, то процесс Yt будет асимптотически самоподобным второго порядка процессом с параметром Херста H = (3 - a )/2. (8) Даже такой простой случай представляет богатые возможности для моделирования трафика, обладающего нужными статистическими характеристиками. Однако, он имеет и определённые ограничения. В частности, одномерное распределение процесса Yt всегда является Пуассоновским с параметром Л = X Ет. Модель трафикас источниками случайной скорости Основное уравнение Рассмотрим ситуацию, когда скорости источников не являются одинаковыми. Пусть St,i(n) =St,i , где все St,i – независимые и одинаково распределенные случайные переменные, принимающие значения в I1 . Как ранее упоминалось,τt,i тоже независимые и одинаково распределенные случайные величины, и St,i и τt,i не зависят и друг от друга. Тогда не трудно показать, что: от EY = X ES X Pr{^ > n} = X ES Et t n = 0 , от qy = X ES2 X Pr{T > n} = X ES2Et , (10) n =0 от ^YrY(k) = X ES2XPr{T > n + k}. n=0 Для этого случая нетрудно доказать теорему, аналогичную теореме из предыдущего параграфа. Используя эти результаты, можно получить процесс с заданной автокорреляционной функцией и одномерным распределением. Для этого необходимо решить следующую задачу – по заданному одномерному распределению трафика найти распределение вероятностей для скорости одного источника. Для вывода основного уравнения воспользуемся аппаратом производящих функций. Пусть скорость отдельного источника имеет производящую функцию от ФS(z) = XPr{S = k}■ zk . (11) k=1 Обозначим количество активных источников в момент времени t за Nt . Как ранее отмечалось, согласно (13) одномерное распределение случайного процесса является пуассоновским с параметром Л, поэтому производящую функцию процесса Yt можно записать как: от Ф, (z) = X Pr{ N = k }(Ф s (z))k = k=0 -лЛk (Ф5 (z )) k = X e ,, = exp(Л(ФS(z) - 1)) ,(12) k =0 k! откуда Фs(z) =1+ л ln( Фy(z ))• (13) Это и есть основное уравнение, связывающее распределение вероятностей для общего трафика с распределением вероятностей скорости одного источника в рассматриваемой модели. Нахождение распределения вероятности источника Использовать полученное уравнение можно различными способами. Здесь мы представим некоторые результаты для случая, когда распределение вероятностей трафика задано в численной форме. Вид распределения неизвестен. Такой случай будет иметь место в ситуации, когда одномерное распределение процесса можно оценить по экспериментальным данным, например, построению гистограммы. Для получения точных результатов нам необходимо сделать следующее ограничение. А именно, скорость источника не может быть нулевой, т.е. Pr{S = 0} = 0 . Это условие имеет вполне понятный физический смысл – источник не считается активным, если в процессе передачи пакеты от этого источника отсутствуют. Пусть нам заданы параметр Херста H и набор вероятностей Pr{Yt = k}, k e 10. Введём обозначение: Лk Pk = ехР(-Л)—, (14) k! Нетрудно видеть, что, учитывая условие ненулевой скорости источника, можно записать Pr{Yt = 0} = p0. Отсюда Л = - log(Pr{Yt = 0}). (15) Кроме того, Pr{Yt = 1} = p 1 Pr{S = 1} , тогда Рг{У = 1} Pr{S=1}= p . (16) Продолжая подобные рассуждения далее, получаем Pr{y = 2} = p 1 Pr{5 = 2} + p 2 Pr{5 1 + 52 = 2} где S1 и S2 – независимые одинаково распределённые случайные переменные с минимальным значением 1. Значит, Pr{51+ 52= 2} = (Pr{5 = 1})2 и Pr{ 5 = 2} = Рг{У = 2} - p2(Pr{5 = 1})2 p1 . (17) Используя такой подход легко получить общее выражение для Pr{5 = k}: РГ{У = k} -^Pm РГ(m^ = k। Pr{ 5 = k} =------------m2------^=1-------,(18) p1 m где Pr{^ 5n = k} может быть найдена, как m-n=1 кратная свёртка моментов конечной последовательности Pr{S=1}, Pr{S=2},…,Pr{S=k-m}, где все эти вероятности известны из предыдущих итераций. Такая итерационная процедура является одним из возможных подходов к численному решению основного уравнения при условии ненулевой скорости источника. Имитационное моделирование Применим полученные формулы для имитационного моделирования самоподобного трафика с заданным одномерным распределением. Для экспериментов были выбраны трассы известной коллекции трасс трафика Ethernet фирмы “Bellcore”. Приведем результаты экспериментов с трассами из файлов “BC-pOct89.TL” и “BC-pAug89.TL”. Файлы типа TL состоят из записей, каждая из которых включает два поля данных, где первое поле – время появления пакета (в секундах, с 6 цифрами после запятой), а второе – размер пакета в байтах. В каждом из использованных файлов содержится 1000000 таких записей. Чтобы преобразовать полученные данные в случайный процесс дискретного времени, мы провели дискретизацию с шагом 15 миллисекунд. Значение процесса равно сумме размеров пакетов, прибывающих в систему в течение соответствующего временного интервала, делённой на размер условной ячейки (использованный размер ячейки 100 байт). Чтобы применить рассматриваемый подход, для каждого из полученных процессов дискретного времени находим эмпирические оценки математического ожидания и дисперсии, а также оцениваем параметр Херста методом частичных дисперсий. По параметру Херста из (8) можно определить необходимое aa, и учитывая, что Pr{r = n} = cons na+1 n = 1,2,... обеспечить выполнение (7). Затем из (15) находим LL, а из (9) ll. Распределение скорости источника вычисляется итерациями (18). Соответствующие вычисления были проделаны для каждой из исследуемых трасс. Необходимо заметить, что итерационная процедура (18), применённая к данным, полученным из гистограммы реального процесса, может на некотором шаге выдать отрицательное значение для очередной вероятности. Это означает, что для имеющихся данных основное уравнение не может быть решено точно. Для нахождения некоторого приближения, нами использовалась следующая эвристическая процедура: каждый раз, когда итерация (18) давала отрицательный результат, соответствующая вероятность принималась равной 0, и вычисления продолжались. Итерации останавливались, когда сумма всех найденных вероятностей становилась больше 1. Последняя вероятность корректировалась так, чтобы сумма равнялась 1. Описанная выше процедура использовалась для получения распределения скорости источника, которое использовалось в программе имитационного моделирования для генерации искусственных трасс трафика. На рис.1 и 2 изображены реальные одномерные распределения реального и сгенерированного с помощью программы имитационного моделирования трафиков для исследуемых трасс. В табл. 1 и 3 приведены Из приведённых данных видно, что предложенный метод хорошо аппроксимирует одномерные распределения процесса (в их начальной части), но первые два момента смоделированного процесса могут весьма сильно отличаться от исходных. Выводы Представленные модель “входная M/G/∞” и метод имитационного моделирования яв- ляются удобным средством для генерации самоподобного трафика в ситуации, когда важно одномерное распределение на начальном участке. Повышение точности аппроксимации первых моментов может являться предметом дальнейшего изучения. Данная работа выполнена при частичной финансовой поддержке Гранта президента Российской Федерации для молодых докторов наук МД-1639.2005.9 и при частичной финансовой поддержке Гранта Научно-образовательного центра “Математические основы дифракционной оптики и обработки изображений” Самарского государственного аэрокосмического университета для молодых учёных, студентов и аспирантов.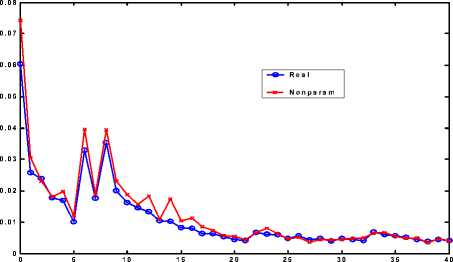
EYt
varYt
H
Real
22,47
1004,03
0,83
Simul
10,04
706,76
0,70
моменты процессов и значения их параметра Херста. В табл. 2 представлена начальная часть распределения скорости источника, вычисленная в соответствии с рассмотренной процедурой.
Список литературы Моделирование самоподобного трафика
- Self-Similar Network Traffic and Performance Evaluation./Ed. by K. Park and W. Willinger. New York: Wiley, 2000.
- V. Paxson and S. Floyd. Wide Area Traffic: The Failure of Poisson Modeling.//IEEE/ACM Trans. Networking, 1995, 3 (3).
- N. Likhanov, B. Tsybakov and N. D. Georganas. Analysis of an ATM buffer with self-similar ("fractal") input traffic. // IEEE INFOCOM'95, Boston, pp. 985-992, April, 1995.


