Моделирование самовоспламенения перед фронтом пламени в двигателе с искровым зажиганием на основе детальной кинетики элементарных реакций
Автор: Сеначин П.К., Сеначин А.П.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Нефтяное, газовое, энергетическое и автотранспортное машиностроение
Статья в выпуске: 1-2 т.13, 2011 года.
Бесплатный доступ
В статье приведены результаты численного моделирования пределов самовоспламенения смесей изооктана и н-гептана перед фронтом пламени в поршневом двигателе с искровым зажиганием в фазовой плоскости частота вращения - угол зажигания при варьировании степени сжатия для смесей различного стехиометрического состава.
Двигатель с искровым зажиганием, фронт пламени, самовоспламенение, стук и детонация, детальная кинетика, моделирование
Короткий адрес: https://sciup.org/148199661
IDR: 148199661 | УДК: 536.46+662.61
Spontaneous ignition modeling before flame front in the engine with spark ignition on the basis of detailed elementary reactions kinetics
In article results of numerical modeling of spontaneous ignition limits of isooctane and n-heptane mixtures before flame front in the piston engine with spark ignition in a phase plane of rotation speed - the spark-ignition angle at variation of compression degree for mixtures of various stechiometric structure are resulted.
Текст научной статьи Моделирование самовоспламенения перед фронтом пламени в двигателе с искровым зажиганием на основе детальной кинетики элементарных реакций
углеводородов [8], результаты расчетов близки к результатам моделирования по ДКМ 284/43 и другим [5-7]. Постановка задачи соответствует работе [9]. Моделирование проводится применительно к характеристикам двигателя автомобиля «Renault Logan» типа «K7J710» размерностью 4Ч 7,95/7 для модельных смесей, соответствующих бензину с октановым числом (ОЧ), равным 90.
Таблица 1. Сокращенный ДКМ смесей изооктана и н-гептана с воздухом
|
№ п/п |
Механизм 43/31 |
|
1 |
С B 7 B Н B 16 B → С B 7 B Н B 15 B + Н |
|
2 |
С B 7 B Н B 15 B → С B 6 B Н B 12 B + СН B 3 B |
|
3 |
С B 6 B Н B 12 B + О B 2 B → С B 2 B Н B 3 B + С B 2 B Н B 5 B + СН B 4 B + СО B 2 B |
|
4 |
С B 7 B Н B 16 B + ОН → С B 7 B Н B 15 B + Н B 2 B О |
|
5 |
С B 7 B Н B 15 B + О B 2 B → С B 7 B Н B 15 B О B 2 B |
|
6 |
С B 7 B Н B 15 B О B 2 B → С B 7 B Н B 15 B + О B 2 B |
|
7 |
С B 7 B Н B 15 B О B 2 B + С B 7 B Н B 16 B → С B 7 B Н B 15 B О B 2 B Н + С B 7 B Н B 15 B |
|
8 |
С B 7 B Н B 16 B + О B 2 B → С B 7 B Н B 15 B + НО B 2 B |
|
9 |
С B 7 B Н B 16 B + СН B 3 B О B 2 B → СН B 3 B О B 2 B Н + С B 7 B Н B 15 B |
|
10 |
С B 7 B Н B 15 B О B 2 B Н → С B 7 B Н B 15 B О + ОН |
|
11 |
С B 7 B Н B 15 B О → С B 6 B Н B 11 B + СН B 3 B + ОН |
|
12 |
С B 6 B Н B 11 B +2 О B 2 B → С B 2 B Н B 3 B + 2 СН B 4 B + 2 СО B 2 B |
|
13 |
С B 7 B Н B 15 B О B 2 B + С B 7 B Н B 15 B →2 С B 7 B Н B 15 B О |
|
14 |
С B 7 B Н B 15 B О B 2 B + НО B 2 B → С B 7 B Н B 15 B О B 2 B Н + О B 2 B |
|
15 |
С B 7 B Н B 15 B + НО B 2 → B С B 7 B Н B 15 B О + ОН |
|
16 |
С B 8 B Н B 18 B → С B 8 B Н B 17 B + Н |
|
17 |
С B 8 B Н B 17 B → С B 6 B Н B 12 B + С B 2 B Н B 5 B |
|
18 |
С B 8 B Н B 18 B + ОН → С B 8 B Н B 17 B + Н B 2 B О |
|
19 |
С B 8 B Н B 17 B + О B 2 B → С B 8 B Н B 17 B О B 2 B |
|
20 |
С B 8 B Н B 17 B О B 2 B → С B 8 B Н B 17 B + О B 2 B |
|
Продолжение таблицы |
|
|
21 |
С B 8 B Н B 17 B О B 2 B + С B 8 B Н B 18 B → С B 8 B Н B 17 B О B 2 B Н + С B 8 B Н 1 B 7 B |
|
22 |
С B 8 B Н B 18 B + О B 2 B → С B 8 B Н B 17 B + НО B 2 B |
|
23 |
С B 8 B Н B 18 B + СН B 3 B О B 2 B → СН B 3 B О B 2 B Н + С B 8 B Н B 17 B |
|
24 |
С B 8 B Н B 17 B О B 2 B Н → С B 8 B Н B 17 B О B B + B B ОН |
|
25 |
С B 8 B Н B 17 B О → С B 6 B Н B 11 B + СН B 3 B + СН B 3 B О |
|
26 |
С B 8 B Н B 17 B О B 2 B + С B 8 B Н 1 B 7 B →2 С B 8 B Н B 17 B О |
|
27 |
С B 8 B Н B 17 B О B 2 B + НО B 2 B → С B 8 B Н B 17 B О B 2 B Н + О B 2 B |
|
28 |
С B 8 B Н B 17 B + НО B 2 B → С B 8 B Н B 17 B О + ОН |
|
29 |
Н + О B 2 B → НО B 2 B |
|
30 |
ОН + Н B 2 B О B 2 B → НО B 2 B + Н B 2 B О |
|
31 |
Н B 2 B О B 2 B →2 ОН |
|
32 |
2 НО B 2 B → Н B 2 B О B 2 B + Н B 2 B О |
|
33 |
СН B 2 B О + ОН → НСО + Н B 2 B О |
|
34 |
НСО + О B 2 B → Н B 2 B О + СО |
|
35 |
СН B 3 B + О B 2 B → СН B 3 B О B 2 B |
|
36 |
СН B 3 B О B 2 B → СН B 3 B + О B 2 B |
|
37 |
СН B 3 B О B 2 B → СН B 2 B О + ОН |
|
38 |
СН B 3 B О B B → СН B 2 B О + Н |
|
39 |
С B 2 B Н B 4 B + ОН → С B 2 B Н B 3 B + Н B 2 B О |
|
40 |
С B 2 B Н B 3 B + О B 2 B → С B 2 B Н B 2 B + НО B 2 B |
|
41 |
С B 2 B Н B 3 B + СН B 2 B О → НСО + С B 2 B Н B 4 B |
|
42 |
С B 2 B Н B 5 B + О B 2 B → С B 2 B Н B 4 B + НО B 2 B |
|
43 |
С B 2 B Н B 5 B + ОН → СН B 3 B + СН B 3 B О |
Vh=V-V bu
,
- динамики скорости горения топливной смеси (массовой доли)
Ff x =——
•
•
2 n n
1 - x
V u
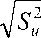
+ ut
где F B f B – площадь поверхности фронта пламени, определяемая как поверхность сферических сечений рабочего объема через приведенную координату фронта пламени r B f B и текущую координату поршня z ; n – частота вращения коленвала;
- нормальной скорости пламени
S u = S u 0 ( pip 0 ) mp ( T .i T « ) m T
,
где S B u0 B – нормальная скорость пламени при нормальных условиях; p 0 B B , T B 0 B – давление и температура при нормальных условиях;
- скорости турбулентных пульсаций на фронте пламени
ut = k nop ^oop ) = 4 rnk пор = 4 > 2 rn (6)
Математическая модель процесса фронтального горения смеси в ДВС с искровым зажиганием и самовоспламенения (теплового взрыва) перед фронтом пламени включает уравнения (в функции угла ПКВ φ ):
- динамики объема для одного цилиндра двигателя
где k B пор B и u пор - эмпирический коэффициент и средняя скорость поршня;
- динамики давления в цилиндре двигателя (энергии всей системы)
p ( V - V« — - Vb — u bp
V C pu C pb J
•
• ( V
- px I —— 1 1 - x
V b
•
V = V c
£ - 1
sin p 1 +
cosP
д/1/ Я 2 - sin2 p?
• • R I H« - pV + x 1 ——
C pb 1 1 - x
- Hb |+Qu r^-+Qb— ub x ) Cpu Cpb (7)
где V = dV/dp- производная объема по углу ПКВ; V B c B - объем камеры сгорания; ε – геометрическая степень сжатия; λ=r/l – отношение радиуса кривошипа к длине шатуна;
- объема свежей смеси (термическое уравнение состояния идеального газа)
V u = ( m a M u » - x ) RT ul P
,
где m B a B – полная масса смеси в цилиндре двигателя; M B u B – средняя молекулярная масса свежей смеси; R – универсальная газовая постоянная; T B u B – температура зоны свежей смеси; p – давление в цилиндре двигателя; x – массовая доля сгоревшей смеси в цилиндре двигателя;
-
- объема продуктов сгорания
где Qu и Qb - теплообмен со стенками цилиндра, поршня и крышки зон свежей смеси и продуктов сгорания соответственно; C B pu B , C B pb B , и H B u B , H B b B - средние молярные теплоемкости и энтальпии свежей смеси и продуктов сгорания;
-
- скоростей химических реакций в зоне свежей смеси
Wt = k p ( pip 0 ) kp n j A ij • exp( - E il RT )
,
(8)-(50)
где k B p B – коэффициент влияния давления на скорость химической реакции; k B i B и E B i B – пре-дэкспонент константы скорости и энергия активации i- ой реакции (таблица 1); A B ij B – концентрации j- ой компоненты частиц, вступающих в i- ю реакцию);
-
- динамики температуры свежей смеси
• г • •
T. = R p + Q u 1
T Cpu p pVu 2mip1"
V7
,
где h B i B – теплота (энтальпия) i- ой реакции;
- средней температуры продуктов сгорания (для идеального газа)
T = pV b M b /( " a Rx )
,
где M B b B – средняя молекулярная масса продуктов сгорания;
- динамики концентраций компонентов свежей смеси (частиц)
холоднопламенной стадии, а при переходе ко второй стадии самовоспламенения, проходит третью точку перегиба. Затем в процессе объемного взрывного горения оставшейся смеси температура резко возрастает. При наступлении холоднопламенной стадии самовоспламенения резко возрастает и затем падает концентрация изооктанового перекисного радикала C B 8 B H B 17 B O B 2 B , при этом максимальное значение концентрации достигает 4600 ppm (рис. 2, линия 2).
• W j
Aj = L + Ai j 2 n n j
••
p - T U
p T
V
RTu
2 n np
1 W i
(53)-(83)
и начальные условия в моменты закрытия впускного клапана (индекс a ) и зажигания (индекс 1):
φ = φ B a B ,… p = p B a B ,… T B u B = T B a B ,… A B j B = A B aj B (84)
φ = φ B 1 B ,… p = p B 1 B ,… T B u B = T B 1 B ,… A B j B = A B aj B (85)
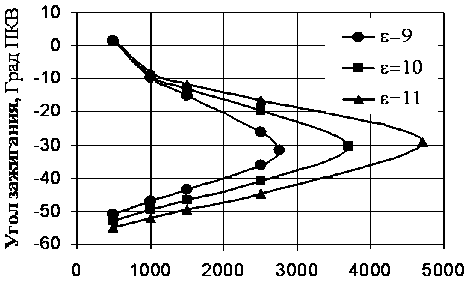
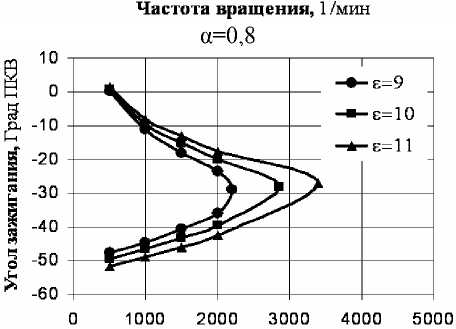
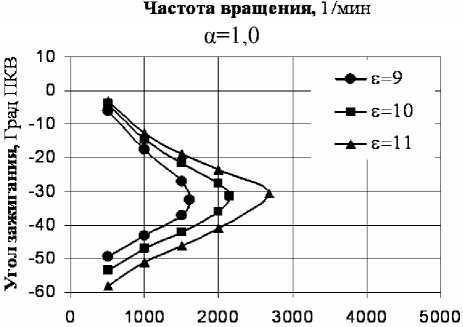
Численное интегрирование системы уравнений (1)-(85) проводилось по собственной программе с привлечением специальных методов интегрирования систем жестких уравнений. На рис. 1 представлены зависимости критического угла опережения зажигания, обеспечивающего сгорание без стука и детонации, от частоты вращения коленчатого вала при различных значениях степени сжатия и коэффициентах избытка воздуха. Характер зависимостей соответствует результатам, ранее полученным в [9] с использованием макроки-нетического уравнения для химической реакции самовоспламенения смеси перед фронтом пламени. Видно, что существует вполне определенная область углов зажигания, для которых в некоторый момент времени фронтальный режим горения смеси переходит в объемный (со стуком или детонацией) из-за самовоспламенения смеси перед фронтом пламени.
На рис. 2 приведена динамика самовоспламенения (теплового взрыва) стехиометрической смеси ( α =1,0) перед фронтом пламени при степени сжатия ε =11 и частоте вращения вала n =2500 мин P -1 P для значения угла зажигания φ B 1 B =30 Град ПКВ. Можно отметить следующие особенности динамики процесса самовоспламенения. Температура смеси перед фронтом пламени T B u B после момента зажигания плавно растет в результате процессов сжатия поршнем и продуктами фронтального горения смеси. Далее она проходит 2 точки перегиба во время
Частота вращения, 1/мин
α=1,2
Рис. 1. Графики зависимостей критического
угла зажигания φ B 1 B от частоты вращения вала n
при различных значениях степени сжатия ε для смесей разного стехиометрического состава. Вне полуострова самовоспламенение отсутствует, внутри полуострова – область стука или
детонации
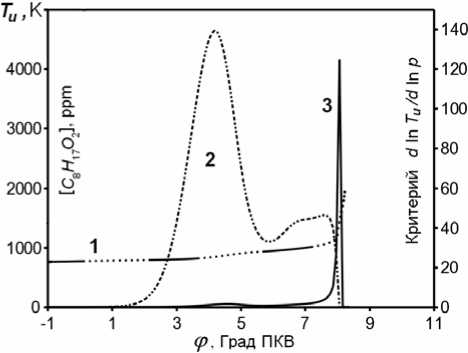
Рис. 2. Динамика самовоспламенения смеси перед фронтом пламени:
1 – динамика температуры смеси перед фронтом пламени T B u B ; 2 – концентрация изооктанового перекисного радикала C B 8 B H B 17 B O B 2 B в единицах ppm; 3 – динамика дифференциального критерия самовоспламенения d ln T B u B / d ln p
Динамика дифференциального критерия самовоспламенения [2]
dT B u B / dp = T B u B / p или d ln T B u B / d ln p = const (86)
(безразмерной функции процесса) следующая. В начале фронтального горения смеси его значение близко к нулю, во время холоднопламенного процесса перед фронтом пламени его величина достигает нескольких единиц (порядка 1-3) и падает практически до нуля. Причем локальный максимум функции совпадает с максимумом концентрации изооктанового перекисного радикала C B 8 B H B 17 B O B 2 B (рис. 2, линия 3). Затем при переходе к второй стадии теплового взрыва величина критерия самовоспламенения снова резко возрастает и достигает максимального значения порядка 120. Поэтому при моделировании углеводородных смесей с детальной химической кинетикой в ДВС с искровым зажиганием в качестве условия самовоспламенения смеси можно принять достижение критерием самовоспламенения d ln T B u B / d ln p численного значения порядка 20-30. Отметим, что ранее при теоретическом решении задач самовоспламенения смеси при адиабатическом сжатии, в том числе в ДВС с искровым зажиганием [2, 9], с уравнением глобальной химической кинетики (макрокинетики), численное значение критерия принималось равным единице d ln T B u B / d ln p =1.
Выводы: численное моделирование самовоспламенения смеси перед фронтом пламени в ДВС с искровым зажиганием с на основе ДКМ 43/31 показывает:
-
- предложенный ДКМ 43/31 для смесей изооктана и н-гептана с воздухом удовлетворительно
описывает процесс самовоспламенения смеси перед фронтом пламени в ДВС с искровым зажиганием и может быть использован для прогнозирования пределов стука или детонации в двигателях;
-
- подтверждено существование полуострова самовоспламенения смеси перед фронтом пламени в фазовой плоскости частота вращения вала – угол зажигания, ранее полученного с использованием уравнения макрокинетики [9]; - с использованием ДКМ подтверждено влияние термодинамических, конструктивно-геометрических, динамических и других параметров процесса на самовоспламенение смеси перед фронтом пламени в ДВС с искровым зажиганием, ранее полученное при использовании уравнения макрокинетики;
-
- при самовоспламенении углеводородных смесей в ДВС с искровым зажиганием динамика температуры перед фронтом пламени имеет три точки перегиба по причине двустадийности процесса;
-
- при самовоспламенении смесей изооктана и н-гептана в ДВС с искровым зажиганием концентрация изооктанового перекисного радикала C B 8 B H B 17 B O B 2 B последовательно проходит четко выраженные максимум и минимум на первой (холоднопламенной) стадии процесса, а на второй стадии (перехода к объемному взрыву или детонации) стремится к нулю, что может быть использовано при численном моделировании процесса;
-
- предложенный в [2] дифференциальный критерий d ln T B u B / d ln p при самовоспламенении смесей изооктана и н-гептана с воздухом в ДВС с искровым зажиганием имеет 2 максимума, причем первый является слабовыраженным с численным значением 1-3 при прохождении холоднопламенной стадии (с дальнейшим снижением практически на порядок), а второй на стадии перехода к взрыву является пикообразным (подобным дельта-функции) с максимальным значением порядка 100-120 с дальнейшим стремлением к нулю (при численных расчетах за критерий самовоспламенения можно положить достижение его значения порядка 20-30).
Список литературы Моделирование самовоспламенения перед фронтом пламени в двигателе с искровым зажиганием на основе детальной кинетики элементарных реакций
- Воинов, А.Н. Сгорание в быстроходных поршневых двигателях/А.Н. Воинов. -М.: Машино-строение, 1977. 277 с.
- Сеначин, П.К. Самовоспламенение газа перед фронтом пламени в закрытом сосуде/П.К. Сена-чин, В.С. Бабкин//Физика горения и взрыва. 1982.Т. 18, № 1. С. 3-8.
- Bradley, D. Influence of Autoignition Delay Time Characteristics of Different Fuels on Pressure Waves and Knock in Reciprocating Engines/D. Bradley, G.T. Kalghatgi//Combustion and Flame. 2009. Vol. 156, No. 8. P. 2307-2318.
- Варнац, Ю. Моделирование процессов горения с помощью детальной кинетики элементарных реакций/Ю. Варнац//Химическая физика. 1994. Т. 13, № 2. С. 3-16.
- Басевич, В.Я. Сокращенная кинетическая схема для моделирования самовоспламенения воздушных смесей изооктана и н-гептана в течение периода индукции применительно к двигателям внутреннего сгорания/В.Я. Басевич, С.М. Фролов//Химическая физика. 1994. Т. 13, № 8-9. С. 146-156.
- Басевич, В.Я. Моделирование самовоспламенения изооктана и н-гептана применительно к условиям ДВС/В.Я. Басевич, А.А. Беляев, В. Брандштетер и др.//Физика горения и взрыва. 1994. Т. 30, № 6. С. 15-25.
- Басевич, В.Я. Моделирование задержек самовоспламенения метановоздушных смесей в двигателе внутреннего сгорания/В.Я. Басевич, В.И. Ведене-ев, В.С. Арутюнов//Физика горения и взрыва. 1994. Т. 30, № 21. С. 7-14.
- Сеначин, А.П. Численное моделирование само-воспламенения смесей изооктана и н-гептана с воздухом перед фронтом пламени в поршневых двигателях с искровым зажиганием/А.П. Сена-чин, П.К. Сеначин//Ползуновский вестник. 2010. № 1. С. 3-12.
- Сеначин, П.К. Самовоспламенение смеси перед фронтом пламени в поршневых двигателях с искровым зажиганием/П.К. Сеначин, В.С. Бабкин, А.В. Борисенко//Физика горения и взрыва. 1997. Т. 33, №6. С. 3-13.
