Моделирование сферического квадратного в плане элемента конструкции из слоистых композиционных материалов

В настоящее время в машиностроении и строительстве большое распространение получили слоистые композиционные материалы, которые состоят из сравнительно податливой матрицы и высокопрочных волокон, армирующих эту матрицу, придающих жесткость и прочность конструкции и несущих основную нагрузку. Матрица, в свою очередь, участвует в перераспределении усилий между несущими слоями и предназначена, в основном, для защиты систем от воздействия неблагоприятных условий окружающей среды, тем самым обеспечивая им надежную работу. Композиционные материалы обладают следующими достоинствами: стойкостью к сырости и коррозии, отсутствием на них отложений и ржавчины, низким коэффициентом теплопроводности. Конструкции из композиционных материалов могут эксплуатироваться в широком диапазоне температур и давлений, в условиях агрессивной среды.

Поскольку экспериментальные исследования прочности слоистых композиционных материалов связаны с использованием дорогостоящего оборудования, то возникает необходимость компьютерного моделирования поведения этих материалов вплоть до разрушения. Анализ литературы показывает, что в настоящее время практически отсутствуют работы в этом направлении, что объясняется значительными трудностями при построении алгоритма расчета с помощью интегрированных систем CAD/CAE.

Элементы конструкций из слоистых композиционных материалов можно представить как многослойный пакет из набора монослоев с различными толщинами и углами ориентации волокон, которые жестко связаны между собой в одно целое. Модули упругости многослойного пакета зависят от жесткостных характеристик слоев определенной ориентации и от соотношения толщин этих слоев в общей толщине пакета [1].

Рассмотрим сферическое квадратное в плане массивное тело со стороной а , изготовленное из слоистого ортотропного материала, загруженое внешним давлением. Тело неподвижно опирается в четырех угловых точках:

При x = ± a y = y min , u = v = 0.

Геометрические параметры тела: сторона квадратного плана а = 50 см; радиус кривизны R = 100 см; толщина h = 5 см.

Упругие постоянные соответствуют такому материалу, как слоистый фенольный стеклопластик, который отличается относительно высокой прочностью и теплоустойчивостью и применяется в качестве конструктивных элементов самолетов, химической аппаратуры; из них изготовляют также трубы, емкости, кожухи и крышки, детали ракет.

Для решения такого рода задач используется следующая методика расчета, которая включает в себя все этапы расчета слоистых композитных материалов, начиная от постановки задачи, построения модели, решения и анализа полученных результатов (рис. 1) [2].

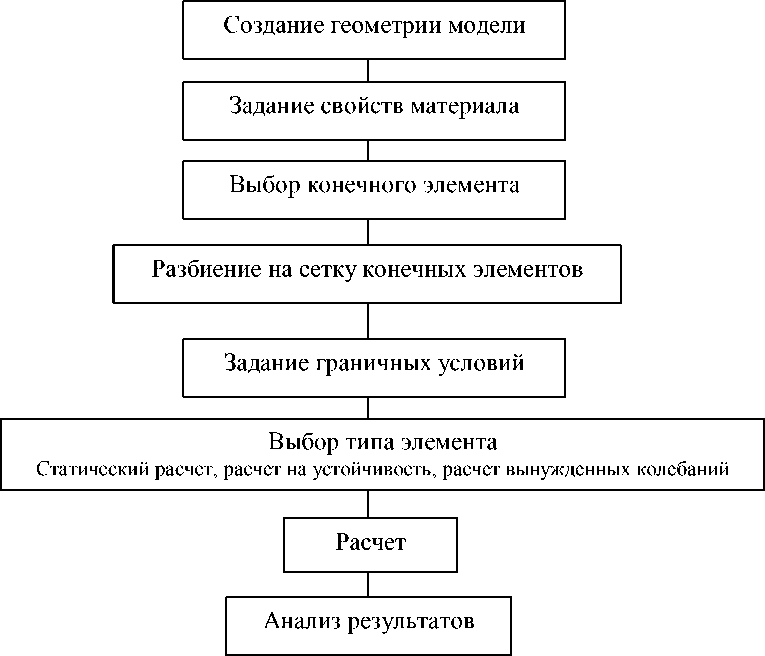
Рис. 1. Основные этапы расчета в пакете ANSYS

Создание модели производится при помощи геометрических примитивов. Для моделирования используется элемент SOLID46 - трехмерный (3D) многослойный объемный элемент задач МДТТ с восемью узлами, предназначенный для моделирования толстых многослойных оболочек или объемных тел [3].

Учитывая симметрию задачи, будем рассматривать лишь четверть сферического тела (рис. 2).

Рис. 2. Массивное тело - часть полой сферы с радиусами R1 = 1,0 м и R2 = 1,05 м

Конечно-элементная модель представляет собой часть полой сферы с радиусами R1 = 1,0 м и R2 = 1,05 м. Тело состоит из десяти слоев одинаковой толщины, имеющих различную ориентацию в пространстве. Угол φ между направлениями главных осей анизотропии и осями локальной системы координат составляет 0⁰, ± 45⁰, 90⁰. Укладка слоев показана на рисунке 3.

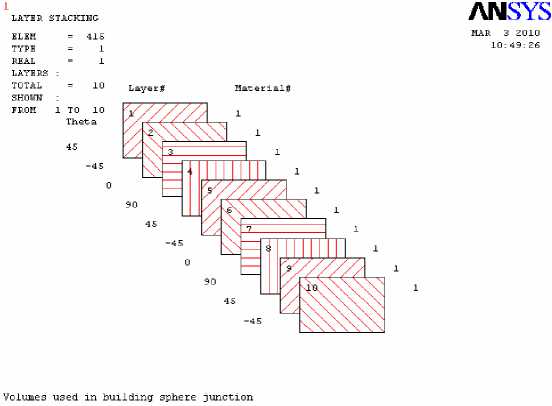
Рис.3. Расположение слоев композиционной модели

Для создания имитации слоистых материалов в работе написаны макросы на языке APDL.

На модель наложена распределенная сетка. Это достигается заданием параметров разбиения линий и наложением регулярной конечно-элементной сетки на модель (рис.4).

Задание внешнего давления и перемещений согласовано с соответствующими граничными условиями (рис. 5).

Рис. 4. Граничные условия конечно-элементной модели

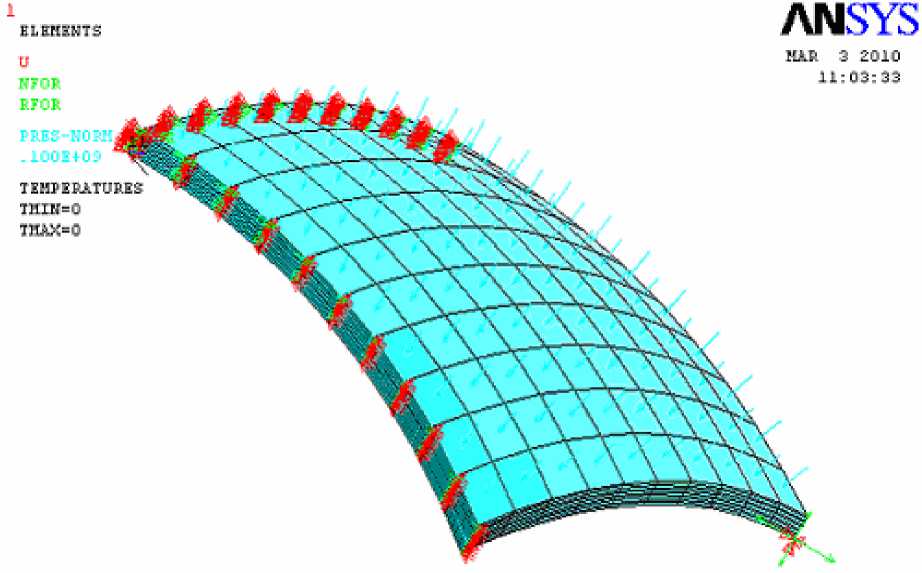
Рис. 5. Внешняя распределенная нагрузка на модель

Полученная система уравнений решается методом Ньютона-Рафсона. При этом задается необходимая точность расчета. На стадии постпроцессорной обработки результатов вычислений получены графические представления результатов счета.

На рисунке 6 показаны деформированное состояние тела и изолинии суммарного вектора перемещений. Наибольший прогиб, как и ожидалось, имеет место в вершине сферической части тела (w max = 47,82 мм), а в правой нижней точке, где тело опирается на основание, перемещения u и v равны 0.

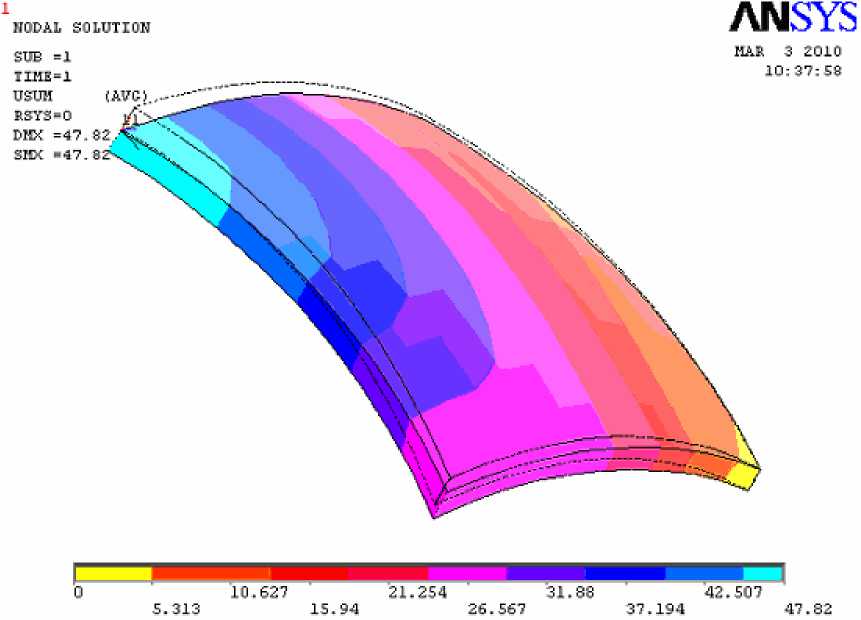
Рис. 6. Деформированное состояние модели. Суммарный вектор перемещений

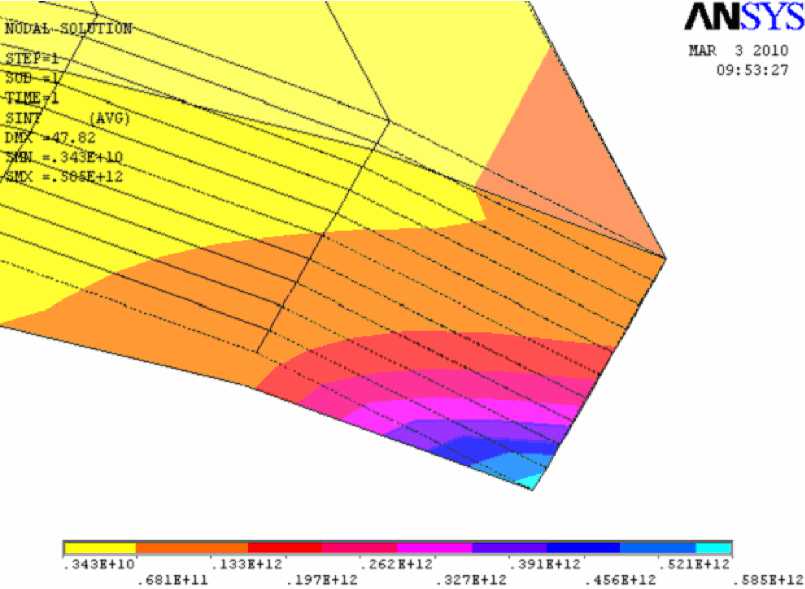
Рис.7. Изолинии интенсивности напряжений в увеличенном масштабе

На рисунке 7 показаны изолинии интенсивности напряжений, вычисленные в каждом слое композита, вблизи от правой нижней опорной точки, где интенсивности напряжений имеют максимальные значения. Анализ распределения напряжений показывает, что начальные разрушения элемента конструкции произойдут именно в опорных угловых точках рассматриваемого элемента конструкции. Изолинии эквивалентных напряжений по Мизесу имеют аналогичный характер, что и интенсивности напряжений.

Когда интенсивности напряжений в опасных точках будут превышать установленные критические значения, тогда в результате разрушения появятся дефекты и трещины, приводящие к перераспределению полей напряжений и деформаций, появлению в окрестностях вершин трещин концентраций напряжений, что, в свою очередь (учитывая равномерность увеличения прикладываемой нагрузки), способствует дальнейшему разрушению тела [4]. Разработанная методика прочностного расчета тел с криволинейными поверхностями может быть полезна на стадии предварительного проектирования в проектных организациях, НИИ и КБ элементов конструкций с заранее прогнозируемыми свойствами, наилучшим образом соответствующими экстремальным условиям эксплуатации изделий.