Моделирование сферолитной структуры в полиэтилене и ее деформирования при нагрузке

The basic purpose of this work consists in the mathematical description of geometry and mechanical properties spherulite formations in polythene structure. Spherulite is a crystallite supramolecular formation as radial focused lamellae with an amorphous phase between them. It is known, that mechanical properties of such polymers at a macrolevel essentially depend on their structure. Therefore the problem of modeling of spherulite geometry and research of its mechanical properties is the important and actual task.

To construct mechanical model of spherulite, taking into account its geometry and mechanical properties. To investigate on its basis of dependence of mechanical properties of the given formation from its deformation.

The received dependencies are supposed to be used at construction of phenomenological model of polythene as elastic - plastic finite deformable continuum.

В настоящее время полиолефины (полиэтилен, полипропилен и т.д.) и композиты на их основе получили широкое применение в различных отраслях промышленности. Это, как правило, блочные частично кристаллизующиеся гибкоцепные полимеры со сложной надмолекулярной структурой [1]. В таких системах наблюдается появление кристаллических образований в виде сферолитов (рис. 1, а ) [5], состоящих из радиально ориентированных ламелей (рис. 1, б ) с аморфной фазой между ними. Сферолиты представляют собой сложные поликристаллические образования, составленные из простейших структурных форм.

Сферолиты растут при кристаллизации полимеров из расплавов, концентрированных растворов высокой вязкости или в полимерах после их переработки в процессе экструзии и литья под давлением. Раз- меры сферолитов – от нескольких микрон до долей миллиметра, а в отдельных случаях они достигают значений порядка сантиметра.

Сферолитам присущи все виды дефектов, характерные для простейших структурных форм, локальные искажения кристаллографических решеток, неупорядоченные поверхности складывания макромолекулярных цепей и т. п. Кроме того, в сферолите даже после завершения кристаллизации часть материала остается аморфной и не входит в кристаллические образования.

Дефекты существенно влияют на механические макросвойства материала. Вот почему проблема моделирования геометрии сферолита и исследование его деформационных свойств является важной и актуальной задачей.

а                        б                           в

Рис. 1. Структура отдельного сферолита ( а ), ветвь сферолита ( б ), фрагмент ламели ( в )

Для того чтобы иметь возможность осуществить такие исследования, был разработан пакет компьютерных программ, позволяющих численно синтезировать структурную морфологию отдельного сферолита и исследовать его механические свойства.

Алгоритм геометрического синтеза основан на выращивании из единого «зародышевого» центра заданного количества ветвей, состоящих из последовательно соединенных случайно ориентированных стержневых элементов. Причем рост этих ветвей производится преимущественно в радиальных направлениях. По мере удаления от центра сферолита эти ветви могут в определенные моменты раздваиваться (в зависимости от заданной вероятности), образуя новые ответвления, которые далее продолжают разрастаться по тем же правилам. Таким образом, алгоритм состоял из следующих операций.

Сначала (первая операция) из некоторого общего центра строится пучок случайно ориентированных стержневых элементов (СЭ), которые являются началами базовых ветвей сферолита. Их число является входным параметром программы.

Затем выполняется операция 2. К свободному концу СЭ пристраиваются один или два новых СЭ, расположенных под заданным углом а к оси уже построенного на предыдущем шаге элемента, то есть он будет совпадать с одной из образующих конуса с углом раскрытия 2а, но вот с какой именно - это вопрос случайный. Таким образом, в случае раздвоения ветви угол между исходящими новыми СЭ может варьироваться в диапазоне от 0 до 2а.

Далее операция 2 применяется для всех вновь появившихся свободных концов ветвей, и так до тех пор, пока сферолит не вырастет до требуемых размеров.

Варьируя значение вероятности возникновения раздвоения ветви, можно задать три возможных варианта развития событий:

• 1)    нет раздвоения (вероятность появления нового ответвления P равна 0);

• 2)    всегда происходит раздвоение ( P = 1);

• 3)    промежуточный вариант (0 <  P < 1).

Расчеты показали, что наиболее близкими к реальности [2, 3] оказались структуры, когда вероятность появления нового ответвления была принята равной 0,6. С помощью данной программы построена геометрическая структура (рис. 2).

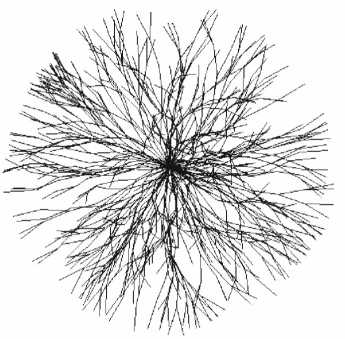
Рис. 2. Геометрическая структура сферолита

С помощью данной программы проведены компьютерные исследования полученных сферолитных структур на фрактальность.

Рассматривался график зависимости количества узлов от расстояния до центра сферолита. Предполагалось, что зависимость можно будет определить по формуле N = CR K , где C - начальное количество узлов, K – фрактальная размерность структуры, R – расстояние до центра сферолита и N – количество узлов.

В логарифмических координатах это должно быть линейной функцией, где К – угол наклона линии. Получен график (рис. 3), где N 0 - начальное количество ветвей, а { l ) - средняя длина ламели. На рисунке можно выделить два типа поведения графика. На участках первого типа количество узлов остается постоянным. Второму типу поведения соответствует плавный рост количества узлов, т.к. длина ламелей изменяется по равномерному закону. Неодинаковая длина ламелей приводит к тому, что доля первого типа уменьшается с ростом радиуса и наблюдается постоянный рост количества узлов. Полученный график нельзя заменить прямой линией, из этого можно заключить, что данная структура не является фрактальной.

С помощью данной программы проведен анализ изменения вдоль радиуса плотности ламелей в зависимости от их ориентации и удаления от центра сферолита.

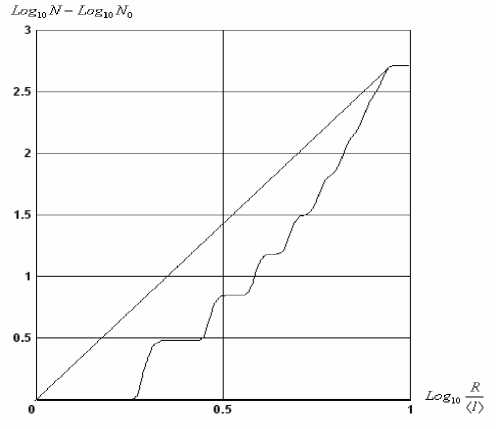
Рис. 3. График зависимости количества узлов, попавших в сферу радиусом R от величины этого радиуса

Была получена зависимость плотности точек раздвоения в шаровом слое заданной толщины в зависимости от удаления от центра (рис. 4, б ). Максимальная плотность достигается при первом разветвлении, т.к. структура создает максимально возможное количество ветвей из аморфного материала окружающего центр роста. Из-за того, что количество узлов растет быстрее, чем объем шарового слоя (рис. 4, а ), возникает второй промежуток роста плотности. Из-за того, что на первом интервале достигается максимальная плотность, на втором промежутке не может быть достигнута большая плотность. И возможны два случая при достижении максимальной плотности на втором промежутке, или сферолит прекращает свой рост, или происходит изменение алгоритма построения и уменьшается вероятность появления узлов. Это также позволяет получить количество начальных ветвлений в зависимости от плотности различных типов полиэтилена.

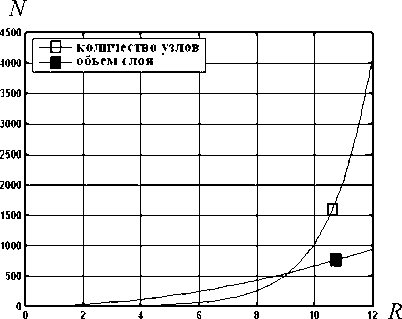
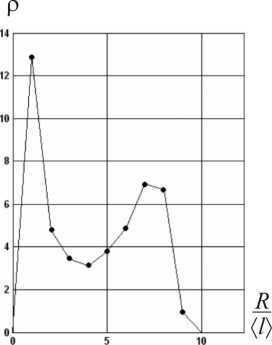
а                               б

Рис. 4. График зависимости количества узлов и объема шарового слоя от расстояния до центра сферолита (а), график зависимости плотности узлов от расстояния до центра сферолита (б)

Исходя из гипотезы об аффинном характере деформирования сферолита и упругом сочленении элементов ламелей, проведена численная оценка энергии деформирования синтезированного на компьютере сферолита в зависимости от его размера и геометрических характеристик – концентрации ламелей и особенностей их ветвления. В программе энергию упругого деформирования рассчитывали по формуле

W = C ∑ ( ϕ i -ϕ i ⁰)² ,                       (1)

i где ϕi – угол между структурными элементами в раздвоении, ϕi0 – исходный угол в ненагруженном состоянии, С – упругая константа). Было установлено, что модельные зависимости W от кратности удлинения сферолита λ (отношение текущего размера сферолита в направлении вытяжки к исходному) близки тем, что описываются с помощью неогуковского потенциала (рис. 5).

w/c

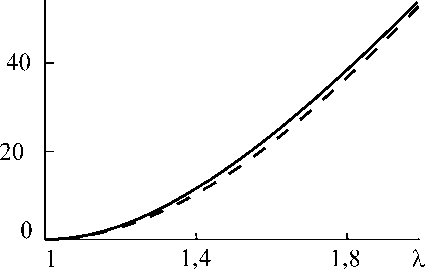
Рис. 5. Зависимость энергии упругого деформирования сферолита от его одноосного удлинения. Сплошная линия – расчет по формуле (1), штриховая – расчет по неогуковской модели

Таким образом, в данной постановке сферолит можно представить как включение из неогукового материала. Расчеты показали, что при увеличении размеров сферолита возрастает его упругая жесткость (рис. 6). Это можно объяснить тем, что возрастает плотность ветвления системы, т.е. чем больше сферолит, тем больше плотность ламелей в нем.

На основании полученных деформационных зависимостей была построена феноменологическая модель сплошной среды, способная испытывать существенно нелинейные упруго-пластические конечные деформации. При этом использовали дифференциальный подход к построению определяющих уравнений, основанный на интерпретации механического поведения материала с помощью символьных схем.

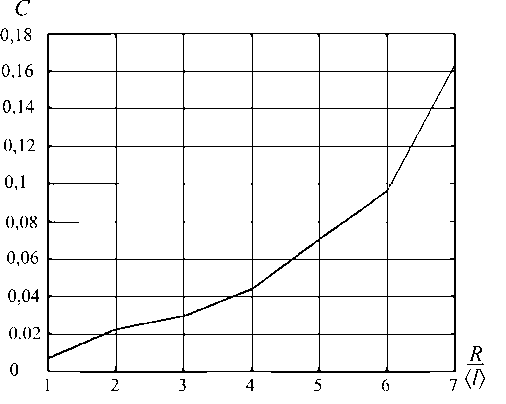
Рис. 6. График зависимости плотности свободной энергии от размера сферолита

Символьная схема модели показана на (рис. 7) [4]. Тогда для упругого элемента (№ 1) тензор скоростей деформации будет равен D 1 =D A – D B , а для пластического (№ 2) D 2 = D B – D C . С учетом неподвижности узла C можно записать

D A =D,    D B =D A – D 1 =D 2 ,    D C =0,            (2)

где D – тензор скоростей деформаций всей среды (его иногда еще называют тензор деформации скорости).

А л J A л В 2 С ^WW^^^f

Рис. 7. Расчетная символьная схема упруго-пластической модели

В схеме последовательного соединения элементов напряжения (усилия) в них должны быть одинаковы. Следовательно, Т 1 = Т 2 = Т.

Для вычисления тензора напряжений Коши в упругом элементе T 1 использовали неогуковские соотношения нелинейной теории упругости. Объем тела и его температура в процессе деформации считали неизменными.

По аналогии с основными уравнениями пластического течения связь между девиатором тензора напряжений Коши пластического элемента T2 и его тензором скоростей пластической деформации D2 записывали как devD2

devD- • devD. , 22devT, dev T2 • dev T2

Зависимость между тензором D 2 и тензором D брали в следующем виде

^ dev D ₂ • dev D ₂ = к^ dev D • dev D ,

где κ – это неотрицательный параметр. Если κ = 0, то материал ведет себя как упругий, при 0 <κ < 1 – как упруго-пластический с упрочнением, при κ > 1 – происходит разупрочнение.

На рис. 8 показаны полученные с помощью данной модели кривые нагружения для полиэтилена высокой плотности (ПЭВП), κ была подобрана таким образом, чтобы наиболее хорошо описать эксперимент.

Таким образом, можно утверждать, что с помощью данного подхода можно получить хорошее соответствие между расчетами и экспериментом.

Если мы будем брать сферолиты различных размеров, то чем больше размер сферолита, тем больше жесткость системы. Причем кривые нагружения будут получаться подобными, и при последующей нормировке они будут совпадать.

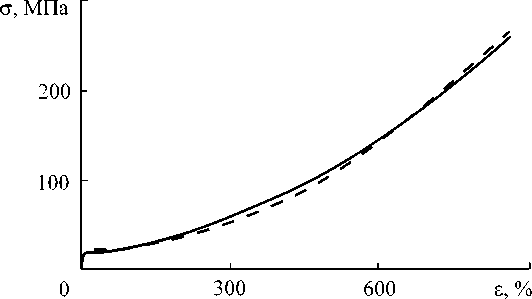
Рис. 8. Зависимость напряжения от деформации при одноосном растяжении для ПЭВП марки «РА».

Сплошная линия – расчет, штриховая – эксперимент

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (Грант 05-08-33361).