Моделирование схемы волоков при помощи покрытия гиперсети взвешенным корневым деревом

СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ

При проведении сплошных рубок леса трелевочный трактор осуществляет доставку сваленных деревьев к верхнему складу по временным транспортным путям, называемым волоками. Трелевочный трактор начинает движение от верхнего склада, подъезжает к месту рубки, полностью нагружается деревьями, возвращается для выгрузки на верхний склад и отправляется за следующей партией леса. Задача состоит в проектировании схемы волоков на территории лесосеки. При этом необходимо учитывать ограничения, связанные с рельефом и свойствами грунта лесосеки, особенностями маневренности трактора.

АНАЛИЗ СУЩЕСТВУЮЩИХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

В работах Э. О. Салминена, С. В. Гурова, Б. М. Большакова, И. В. Григорьева [1], [5] исследована задача определения схемы волоков на лесосеке с учетом некоторых свойств грунта. В модели территория лесосеки разбита на не-пересекающиеся квадратные участки (участки набора пачки деревьев). Каждому участку поставлено в соответствие число – обобщенный коэффициент, характеризующий степень воздействия трелевочного трактора на грунт участка. Однако заметим, что участок сбора пачки деревьев имеет достаточно большие размеры и в условиях пересеченной местности не может быть однозначно охарактеризован одним значением, показывающим свойства грунта.

Следовательно, при моделировании лесосеки логично разбивать ее территорию на более

мелкие непересекающиеся участки, характеризуемые консистенцией грунта, высотой над уровнем моря и объемом произрастающего леса. Сбор одной пачки деревьев в таком случае осуществляется с нескольких участков. Такая модель лучше учитывает непригодные и малопригодные для проезда техники участки.

ПРИМЕНЕНИЕ ТЕОРИИ ГИПЕРСЕТЕЙ И ГИПЕРСЕТЕВОЙ ТЕХНОЛОГИИ

Теория гиперсетей, изложенная в работах В. К. Попкова, Г. Ы. Токтошова [2], [3], [4], применяется для моделирования задач сложной сетевой структуры, таких как строительство инженерных сетей электросвязи, сетей автомобильных дорог, нефтепроводных, газопроводных сетей и пр. Гиперсетевая технология описывает процесс формализации исходной задачи и построения соответствующей иерархической гиперсети. В данной статье гиперсетевая технология применена для моделирования схемы первичного транспорта древесины.

Математическая модель лесосеки построена в виде двухуровневой гиперсети специального вида. Нижний уровень гиперсети является гиперграфом, построенным методом сеток [4], [6], верхний уровень – ориентированным графом, узлы которого соответствуют гиперребрам нижнего уровня.

ОПИСАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

Пусть область D представляет собой проекцию территории лесосеки на плоскости xOy . Разобьем область D регулярной сеткой с шагом l (м), образованной двумя семействами прямых:

параллельных оси Oy и параллельных оси Ox . Сопоставим каждой клетке сеточной модели территории лесосеки вершину гиперсети.

Определим гиперсеть A - ( V , W , E , F ', F ' , G ) , в которой V - множество вершин, W - множество гиперребер, E - множество дуг, F ^/ : W ^ 2 ^V , F¹ : W ^ 2 ^V - отображения, ставящие в соответствие каждому гиперребру w е W два подмножества F ^/ ( w ) с V и F " ( w ) с V его вершин, F ^/ определяет упорядоченное множество вершин, соответствующих участкам непосредственного проезда трелевочного трактора, F " - множество вершин, соответствующих участкам, которые попадают в зону охвата манипулятора трелевочного трактора. G : E ^ W х W - инъективное отображение, ставящее в соответствие каждой дуге e е E упорядоченную пару G ( e ) - ( w , ( e ) w ₂ ( e )) гиперребер множества W, w , ( e ) и w ₂ ( e ) - обозначения для первого и второго элементов пары G ( e ). , .

Таким образом, тройки A ', = ( v , W , F / ) , A '] = ( v , w , f ' ) являются гиперграфами, а тройка A ₂ = ( w , E , G ) - орграфом. В орграфе A ₂ гиперребра множества W будем называть узлами.

Пусть T - ( S , r , p ) - корневое дерево в орграфе A ₂, в котором S с W - множество узлов дерева, r е S - корень дерева, p : S ^ S - отображение, ставящее в соответствие каждому узлу s е S его родителя p ( s ) в дереве. Это означает, что если дереву T принадлежит дуга ( w , , w ₂), то p ( w , ) = w ₂ (все дуги корневого дерева направлены к корню).

Очевидно, что отображение p должно обладать следующими свойствами: 1) p ( r ) = r ; 2) для любого s е S p (•• p ( p ^{( s} ))-)^- r .

1442443 S

Второе свойство означает, что из любого узла дерева существует путь до корня, состоящий из дуг дерева.

Будем говорить, что дерево T - ( s , r , p ) покрывает вершину v е V, если существует s е S , для которого v е F " ( s ) . Назовем корневое дерево T покрывающим деревом гиперсети A , если U F " ( ^ ) = V . Таким образом, покрывающее дерево гиперсети покрывает все его вершины.

Обозначим как J упорядоченное индексное множество консистенций грунта, J = {1, .., k }. Будем считать, что при увеличении индекса тип консистенции грунта будет улучшаться. Обозначим как I упорядоченное индексное множество категорий глубины колеи, I = {1, ..., g }. Будем считать, что при увеличении индекса категория глубины колеи будет улучшаться.

Для каждой вершины v е V гиперсети известны следующие характеристики: ц ( v ) е J - консистенция грунта, R ( v ) - высота над уровнем моря (м), K ( v ) - запас леса (м³).

Для каждого гиперребра w е W определим n(w)е J - консистенцию грунта как наихудшее значение консистенции грунта по всем вершинам множества F/(w):

Q ( w ) = min д ( v ) , V w е W. v e F / ( w )

Для каждого гиперребра w е W обозначим начальную вершину beg ( w ) е F / ( w ) и конечную вершину end ( w ) е F / ( w ) . Пара вершин m ( w ) = ( beg ( w ), end ( w )) является направленным отрезком, определяющим траекторию и направление движения трелевочного трактора при сборе леса с территории, соответствующей гиперребру. Обозначим ф^, (⁽ W ) - угол между отрезками соответствующих смежных гиперребер гиперсети.

Пусть z_w = | f ^z ( w ) - мощность множества F ' ( w ) , w е W. Обозначим q = { v , , v ₂, ., v _z } е F / ( w ) -последовательность вершин вдоль направленного отрезка из множества F / ( w ) для гиперребра w е W .

Для каждого гиперребра w е W определим перепады высоты между соседними вершинами последовательности q :

R ', - 1 ^{( w} ) = R ⁽ v ) - R ⁽ _{Ч - 1} ) , V i = 2, ., z w , V w е W .

Пусть n - | S | - мощность множества S . Назовем корневое дерево T помеченным , если все его узлы пронумерованы числами от 1 до n в порядке обхода трелюющим трактором территории, соответствующей узлам, при сборе леса. Тогда для каждого узла s е S обозначим через v T ( s ) множество узлов дерева T , у которых номера меньше, чем номер узла s , то есть соответствующая территория обходится трелевочным трактором раньше.

Для каждого узла s е S дерева T определим остаточное множество:

U T ( s ) = F¹¹ ( s ) \

(

U F "  ( w ) , V s е S .

^ w ev T ( s )         ^

Для каждого узла s е S дерева T определим остаточный запас леса:

K_T ( s ) = ^ K ( v ), s е S .

v e U t ( s )

Обозначим h ( s ) - число потомков узла s е S в дереве T . h ( s ) определяет количество проездов по территории волока, соответствующего узлу s е S .

Пусть задана функция Ф : J х Z ⁺ ^ I , такая что для фиксированного j е J Ф( / , h ) как функция от h е Z ⁺ является неотрицательной возрастающей вогнутой функцией. Функция Ф определяет зависимость образования категории колеи для каждой консистенции грунта в зависимости от числа проездов трелевочного трактора.

В качестве критерия оптимальности задачи определим лексикографическую целевую функцию (y,(T), .,yg(T)) ^ min, которая минимизи- рует количество узлов дерева, соответствующих территории пролегания участков волока по приоритетам в порядке возрастания индекса категории колеи. Компонента вектора yt(T) – число узлов множества S дерева T, соответствующих волокам с индексом категории глубины колеи t, t E {1, g}:

yt (T )=# {s|s e 5, t = Ф(П(s), h (s))}.

Сформулируем задачу. Для заданной гиперсети A и чисел P ₀, P , α , l , γ ^/ , γ ^// требуется найти корневое помеченное покрывающее дерево T = ( S , r , p ), для которого вектор ( y ₁( T ), …, y_g ( T )) принимает минимальное значение, при этом:

• 1.    Для каждого узла s ∈ S дерева T остаточный запас P ₀ ≤ K_T ( s ) ≤ P , ∀ s ∈ S , где [ P ₀, P ] – допустимый интервал объема пачки леса (м³) для трелевочного трактора.

• 2.    Для каждой пары смежных узлов дерева T угол между направленными отрезками смежных узлов ограничен α , α – недопустимый угол поворота трелевочного трактора:

• 3.    Для каждого узла s ∈ S дерева T перепады высот между соседними участками лежат в пределах [tg ( y ^Z/ ) l , tg ( Y 0 l ]: Y' < 0, Y" - 0, Y' — мак— симальный угол наклона при движении трелевочного трактора вверх, γ ^// – максимальный угол наклона при движении трелевочного трактора вниз, l – шаг (м) накладываемой сетки:

Ф т ( W ) <  a , p ⁽ s ) = w, s , w E S .

?g ( / / ) l <  R 'i - i ( s ) <  Zg ( / // ) l , V i = 2, _, z s , V s E S .

Искомое дерево определяет схему волоков, корень дерева указывает место погрузочного пункта.

АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

Алгоритм решения рассмотренной задачи основан на поиске с возвратом. Вначале корневое дерево состоит из одного узла. Затем на каждой итерации ищется дуга, добавление которой в дерево приведет к наименьшему увеличению значения целевой функции. Поиск такой дуги осуществляется перебором всех возможных вариантов добавления не более чем N дуг в дерево. Параметр N подбирается в зависимости от числа узлов орграфа второго уровня.

Приведем псевдокод предложенного алгоритма построения покрывающего дерева гиперсети T с корнем r .

FindTree ( T , r , N )

T = tree( r )

while not cov(T, V) do e/ = argmin{g (add(T, e), 1, f(T), area (T), N) | e e set (E, T)}

T = add( T , e ^/ )

return T

В начале алгоритма FindTree дерево T состоит из одного корня r . Затем на каждой итерации цикла while перебираются все возможные варианты траекторий добавления в дерево не более чем N дуг. Лучшей признается та траектория, для которой отношение приращения целевой функции задачи к приращению числа покрытых вершин будет минимальным. В результате в дерево добавляется первая дуга лучшей траектории. Этот процесс повторяется до тех пор, пока дерево не покроет все вершины гиперсети.

Функция tree( r ) строит начальное дерево T , состоящее из одного корня r . Функция cov ( T , V ) проверяет покрытие вершин гиперсети деревом, возвращает истину, если все вершины покрыты, иначе ложь. Множество первых дуг траекторий генерируется при помощи функции set( E , T ). Функция add( T , e ) формирует новое дерево с добавленной в него дугой e и возвращает его. Функция f ( T ) рассчитывает и возвращает целевую функцию задачи для дерева T . Функция area( T ) возвращает множество вершин, покрытых деревом T . Функция g (…) перебирает траектории добавления не более чем N дуг и возвращает минимальное отношение приращения целевой функции задачи к приращению числа покрытых вершин.

Временная сложность алгоритма в худшем случае равна O (| V|²N ^{+ 1} ) , так как на каждом шаге перебирается не более чем V ^{2 N} траекторий добавления не более чем N дуг и добавление каждой дуги должно покрыть как минимум одну новую вершину.

ТЕСТОВЫЙ ПРИМЕР

Проиллюстрируем результат работы алгоритма на примере (рис. 1). Расчет произведен на гиперсети с 988 вершинами, 840 гиперребрами (узлами), более чем 10 000 дугами. Параметр N (глубина перебора вариантов дуг) равен 2.

Для примера использованы данные одного из лесозаготовительных предприятий Карелии. На рис. 1 территория лесосеки закрашена оттенками серого цвета, и чем темнее участок, тем меньше устойчивость грунта. Черным квадратом отмечено место размещения верхнего склада. Рассчитанная схема волоков содержит 45 волоков, из них 2 участка волока с недопустимой глубиной колеи, 1 – с критической глубиной колеи, 20 – с глубокой колеей, 22 – с рекомендуемой глубиной колеи. На рис. 1 чем больше толщина линии, тем больше глубина колеи волока.

На рис. 2 приведена схема волоков, рассчитанная на тех же данных о лесосеке методом динамического программирования, изложенным в [5]. В качестве территории сбора пачки деревьев взяты укрупненные участки (квадраты 3 х 3 деления сетки), данные о свойствах грунта для укрупненных участков – усредненные значения данных с участков, попавших внутрь квадрата.

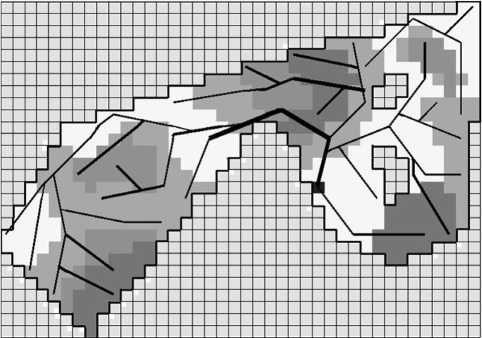
Рис. 1. Схема волоков, полученная алгоритмом FindTree на гиперсети

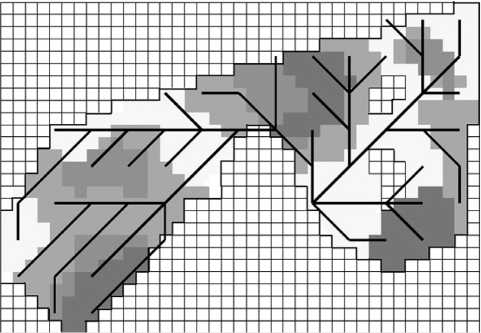
Рис. 2. Схема волоков, полученная методом динамического программирования на графе

гиперсети, для него можно определить значения целевого вектора ( y ₁( T ),…, y_g ( T )). Этот вектор используется для сравнения рассчитанных разными методами схем волоков. При этом глубина колеи рассчитанной схемы волоков определялась так же, как глубина колеи в гиперсетевой модели.

В результате схема волоков содержит 61 волок: из них 3 участка волока с недопустимой глубиной колеи, 4 – с критической глубиной колеи, 26 – с глубокой колеей, 28 – с рекомендуемой глубиной колеи. Увеличение общего количества участков волоков объясняется фактическим расширением границ территории лесосеки в процессе укрупнения участков. В целом заметно увеличение количества участков с недопустимой и критической глубиной колеи, также волока проходят по непригодным для проезда местам.

В таблице представлены средние процентные отношения количества волоков с различным видом колеи в решениях, полученных при сравнении предложенных методов на 15 примерах.

Сравнение процентного отношения количества волоков с различным видом колеи в решениях

Колея	Предложенный алгоритм на гиперсети, %	Метод динамического программирования на графе, %
Недопустимо глубокая	4	5
Критическая	2	6
Глубокая	45	43
Рекомендуемая	49	46

ЗАКЛЮЧЕНИЕ

Для сравнения схем была построена гиперсеть, вершины которой соответствуют участкам (квадратам 1 х 1), гиперребра - территориям сбора пачки леса (квадратам 3 х 3). Гиперребра образуют разбиение множества вершин. Дуги связывают гиперребра, соответствующие соседним квадратам 3 х 3. Подмножествам вершин, по которым проходит волок, соответствуют квадраты 1 х 1, пересекающиеся с отрезками, соединяющими центры квадратов 3 х 3.

Полученной методом динамического программирования схеме волоков соответствует корневое покрывающее дерево T построенной

В работе впервые применен гиперсетевой подход для моделирования схемы трелевочных волоков на лесосеке. Проведение тестовых испытаний подтверждает получение лучших решений по сравнению с решениями, полученными на графовых структурах, благодаря большей гибкости гиперсетевых структур. Рассмотренная математическая модель и алгоритм позволяют решать задачу определения схемы волоков на лесосеке неправильной формы, с неравномерной плотностью произрастания леса, разными зонами устойчивости грунта и значительными перепадами высот, что часто встречается на практике.