МОДЕЛИРОВАНИЕ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ С РАВНОМЕРНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ

Рассмотрим систему массового обслуживания (СМО), в которой интервалы между поступлениями требований τ_λ и случайные времена их обслуживания τ_μ описываются функциями плотности равномерного закона распределения:

0, t < a, fl (t) = S1/ (b - a), a < t < b,

0, t >  b ,

0, t <  c,

f? ( t ) = i 1/( c - d ), c <  t <  d ,

0, t >  d.

Следовательно, интервалы между соседними моментами поступлений требований распределены равномерно на интервале ( a , b ), а случайное время обслуживания – на интервале ( c , d ). Для существования стационарного режима функционирования такой системы должно выполняться условие – коэффициент загрузки системы 0 <  ρ < 1. Коэффициент загрузки системы как всегда определяется соотношением двух средних значений интервалов ρ = τ _µ / τ _λ . В случае применения равномерных законов распределений средние значения совпадают с серединами рассматриваемых интервалов и условие для стационарного режима функционирования системы примет вид: ( c + d )/2 < ( a + b )/2.

Как уже было отмечено, ни в научных статьях по массовому обслуживанию, ни в многочисленных книгах на эту тему нет упоминаний о равномерном законе распределения вероятностей [1–5] и др. Более того, в трехпозиционной символике Кендалла классификации СМО нет даже места в контексте описания рассматриваемой системы.

В имитационном моделировании все обстоит иначе. В большинстве книг по дискретно-событийному моделированию, в частности, по GPSS WORLD [6–13], можно найти множество примеров успешных имитационных моделей СМО с применением равномерного закона распределения. Следует отметить также, что этот закон распределения занимает важное место в имитационном моделировании. Продемонстрируем сказанное на примере.

Равномерный закон распределения вероятностей на интервале (0, 1) является основополагающим в имитационном моделировании. Генераторы псевдослучайных последовательностей для этого закона входят в библиотеку программного обеспечения любых персональных компьютеров в виде библиотечных функций. На основе этого генератора могут быть сгенерированы случайные величины, распределенные в соответствии с любым законом распределения по известным алгоритмам [10]. Возьмем, например, экспо-

ненциальный закон распределения с функцией плотности / % ( x ) = 2 e^-Zx. Сгенерируем случайную величину X на интервале (0, 1), вычислим натуральный логарифм ln X, умножим ln X на величину -1/λ. В итоге получим экспоненциально распределенную случайную величину – (1/λ) ln X , со средним значением 1/λ. В этом и заключается алгоритм преобразования равномерно распределенной случайной величины на интервале (0, 1) в экспоненциально распределенную случайную величину.

Корректность этого алгоритма может быть продемонстрирована следующим образом. Функция F ( x ) распределения вероятностей случайной величины X определяется для любого действительного аргумента х как вероятность события F ( x ) = Р ( Х<х ). Для экспоненциального закона распределения со средним значением 1/λ функция распределения примет вид

x

F ( x ) = f X e ^-X t dt = 1 - e ^{-Z x} .

Тогда

P ( - -ln X <  x ) = P (In X > X x ) = P ( X >  e ^{X x} ) =

X

= P ( e -^{X x} <  X <  1) = 1 - e ^{X x} .

Таким образом, убеждаемся в том, что вышеописанный алгоритм обеспечивает генерацию экспоненциально распределенной случайной величины. Аналогично дело обстоит и с другими законами распределений. Таким образом, генератор псевдослучайных чисел на интервале (0, 1) играет фундаментальную роль в имитационном моделировании [10].

Постановка и решение задачи

В статье ставится задача выяснения того факта, почему в теории массового обслуживания не рассматриваются системы, функционирующие в соответствии с равномерным законом распределения вероятностей и выясняется причина отсутствия решения для этого случая. Известно, что основным инструментарием вывода решений в теории массового обслуживания являются теория марковских процессов и метод спектрального решения интегрального уравнения Линдли. В то же время, в практике имитационного моделирования СМО, в частности в GPSS World, равномерный закон занимает лидирующие позиции.

Рассмотрим первую часть поставленной задачи, а именно метод спектрального решения интегрального уравнения Линдли для систем, функционирующих по закону равномерного распределения вероятностей исходных временных интервалов поступлений и обслуживания. Сам метод подробно и с приведением конкретных примеров описан в [1]. С использованием вышеуказанного метода авторами данной статьи и получены результаты для множества СМО. Этот метод применяется во многих областях науки и техники [1; 14–18].

Далее, в первую очередь определим необходимые нам для решения поставленной задачи изображения функций плотности распределения вероятностей Лапласа (1), которые обозначим как F _x ( s ) и F ^ ( s ) соответственно:

F a s )=

b

—J e “ ^stdt = b - a a

d

FAs ) ⁼ 1— ^ ^C st dt ⁼ d - c c

- bs   -~ as e - e s (a - b)

,

- ds     - cs e - e s (c - d)

Убедимся в правильности этих преобразований (2), а для этого найдем среднее значение интервала между соседними поступлениями, т.е. математическое ожидание для равномерного закона распределения вероятностей, а оно как известно равно середине интервала ( a , b ).

Значение первой производной со знаком минус от функции F_λ *( s ):

d ds

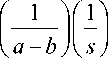
(e ^{- bs}

—

e ^{- as} )

e-as - e-bs   ae-as - be-bs s 2( a - b)      s (a - b)

lim s ^0

e ^{- bs} + bs e ^{- bs} s ²( a - b )

e ^{- as} ( as + 1) s ²( a - b )

a ² - b²   a + b

2( a - b ) =

Следовательно, изображения Лапласа (2) определены корректно.

Как того требует метод спектрального решения, попытаемся сконструировать для выражения, составленного из изображений Лапласа F * ( - s ) • F * ( s ) - 1 представление в виде дробно-рациональной функции s : а ( s )/ в ( s ) в комплексной плоскости для определения его нулей и полюсов. Таким образом, промежуточная задача сводится к построению выражения:

**

^f x ( ^{- s} ) • F ( ^s ) ^{- 1} = ^{а ( s} )/ P ^{( s} ) .        (3)

Подставив в (3) компоненты (2), получим спектральное разложение решения интегрального уравнения Линдли для нашей системы, которое принимает вид:

F ( - s ) • F ( s ) - 1 =

bs

^^^^.

e as ) x

x

- cs

^^^^B

e

- ds

) - 1 =

(e as - e ^{b s} )(e ^- cs - e ^{- ds} ) - s ²( a - b )( c - d ) s ² ( a - b )( c - d )

В числителе разложения (4) фигурируют четыре экспоненты, что свидетельствует о том, что для СМО согласно равномерному закону распределения при спектральном решении интегрального уравнения Линдли не удается получить дробно-рациональной функции в комплексной плоскости s. Следовательно, с использованием данного метода для такой системы нельзя получить точное аналитическое решение для среднего времени ожидания требований в очереди. При этом возможность получения решения с использованием других методов исключать нельзя.

Теперь попробуем получить приближенное решения с помощью этого же метода. Для конструирования рациональной функции s в (4) попробуем разложить показательные функции в ряд Маклорена:

e^x = 1 + x + x 2 /2+x 3 /31+ ...        (5)

ограничимся тремя первыми слагаемыми ряда (5).

Для этого рассмотрим пример 1. Возьмем интервал поступления требований ( a , b ), где a = 0,5, b = 1,5, а для времени обслуживания интервал ( c , d ), где c = 0,4 , d = 1,4.Тогда середины отрезков будут равны ( a + b)/ 2 = 1,0, ( c + d ) / 2 = 0,9 , что обеспечивает коэффициент загрузки системы р = 0,9. Спектральное решение для этого примера принимает вид:

(1 + 0,5 s + 0,125 s ² - 1 - 1,5 s - 1,125 s 2 )/ s ² x

x (1 - 0,4 s + 0,08 s ² - 1 + 1,4 s - 0,98 s 2 ) - s ² =

= 0,9 s ² - 0,1 s - 2,0.

Числитель разложения согласно методу спектрального разложения должен иметь в качестве нуля число s = 0, но это условие не выполняется. Поэтому делаем вывод, что для рассматриваемой нами системы методом спектрального решения нельзя получить даже приближенного

аналитического решения. Таким образом, ни для какой СМО, в состав которой входит равномерный закон распределения, нельзя построить аналитическое решение для оптимизации задержки требований в очереди методом спектрального решения, тем самым, надо попытаться использовать другие методы.

Решение поставленной задачи наоснове имитационного моделирования

Универсальная система дискретно-событийного моделирования GPSS WORLD не нуждается в рекламировании. Она разработана для оценки эффективности различных систем, представимых в виде систем массового обслуживания [6–13] и включает в виде библиотечных программ множество генераторов псевдослучайных последовательностей для различных законов распределений.

Для вышерассмотренного примера 1 построим имитационную модель в системе GPSS WORLD. Увеличив масштаб модельного времени в 10 раз, избавимся от нецелочисленных значений a , b , c , d . Ниже приведен текст программы на GPSS WORLD.

10 GENERATE 10,5

20 QUEUE QCHAN

30 SEIZE CHAN

40 DEPART QCHAN

50 ADVANCE 9,5

60 RELEASE CHAN

70 TERMINATE 1

80 START 1000000

Ниже на рисунке 1 приведен фрагмент стандартного отчета GPSS для примера 1. Весь отчет занимает много места, здесь же мы ограничимся только фрагментом из основных характеристик СМО.

Из отчета следует, что всего было сгенерировано 1000001 транзакт, их прогон через модель приводит к формированию следующей статистики: загрузка системы ρ = 0,900, среднее время обслуживания T_z = 8,996 единиц модельного времени, среднее время ожидания в очереди W = 6,224 единиц времени, а средняя длина очереди N q = 0,622. Анализ этих результатов в сравнении с исходными данными для имитационной модели свидетельствует о том, что эта модель работает идеально.

CHAN 1000001 0.900  8.996   1  1000001 000     0

QCHAN 10   1  1000001 299046     0.622     6.224    8.880   0

Рисунок 1. Фрагмент стандартного отчета системы GPSS для примера 1

Заметим, что при имитационном моделировании СМО относительно небольшое число статистических испытаний отражает работу системы в переходном режиме. Мы в демонстрационных примерах использовали большое число испытаний, что отражает функционирование системы в стационарном режиме.

Пример 2. Рассмотрим в качестве интервала поступлений требований ( a , b ) интервал (1,5; 2,5) со средним значением в 2,0 единицы модельного времени. Возьмем в качестве закона обслуживания экспоненциальный закон распределения вероятностей со средним значением 1,8 единиц времени, что дает нам коэффициент загрузки, равный 0,9. Опять увеличиваем масштаб времени в 10 раз, чтобы исключить из рассмотрения дробные числовые значения.

Ниже приведен текст программы на GPSS WORLD.

10 GENERATE 20,5

20 QUEUE QCHAN

30 SEIZE CHAN

40 DEPART QCHAN

50 ADVANCE (Exponential(11,0,18))

60 RELEASE CHAN

70 TERMINATE 1

80 START 1000000

На рисунке 2 приведен фрагмент стандартного отчета GPSS.

Из этого отчета следует, что в ходе работы программы сгенерировано 100000 транзактов, прогон которых через имитационную модель, дает следующую статистику: загрузка системы p = 0,901, среднее время обслуживания Т = 18,013 единиц модельного времени, среднее время ожидания в очереди W = 77,617 единиц времени, а средняя длина очереди N_q = 3,881 требований. Результаты моделирования практически идентичны исходным данным имитационной модели. Таким образом, с использованием универсальной системы имитации GPSS World можно моделировать СМО с применением равномерного закона распределения в сочетании с множеством других законов распределений.

Заключение

В соответствии с полученными результатами можно сделать следующие выводам. Частично получен ответ на вопрос, почему же в теории массового обслуживания не рассматриваются системы, функционирующие в соответствии с равномерным законом распределения вероятностей, хотя он стоит на первом месте в курсе теории вероятностей. Показано, что для таких СМО нельзя получить аналитическое решение методом спектрального решения для среднего времени ожидания требований в очереди, следовательно, аналитически не могут быть определены и остальные характеристики функционирования СМО, являющиеся производными от среднего времени ожидания. Поэтому следует попытаться получить это решение другими методами.

Мы также убедились, что такие системы хорошо моделируются средствами имитационного моделирования, в частности на GPSS WORLD. При этом в известной литературе по системе GPSS WORLD рассмотрение примеров моделирования СМО начинается именно с равномерного закона распределения.

Данный случай можно отнести к парадоксу теории массового обслуживания, когда для самого простого закона распределения из курса теории вероятностей невозможно построить аналитическое решение для среднего времени ожидания требований в очереди методом спектрального решения интегрального уравнения Линдли. Для всех других систем, не относящихся к равномерному закону, это решение находится.