Моделирование системы смазки редуктора хода экскаватора

Одна из важнейших характеристик работоспособности любого оборудования – ресурс. Причем зачастую эта характеристика более важна, чем масса, габариты или цена. Увеличения ресурса механизма можно добиться несколькими методами, в том числе применением более прочных материалов, улучшением качества обработки сопрягаемых поверхностей, более точной подачей смазки; путем применения принципиально новых механизмов с большим ресурсом, чем у стандартных механизмов.

Для увеличения ресурса экскаватора КТМ-405т Красноярского завода тяжелого машиностроения используются все вышеперечисленные методы. Так, например, в этом экскаваторе отказались от гидравлических толкателей приводов напора и подъема. Вместо них применены механические толкатели, основное преимущество которых заключается в том, что привод толкателей работает только при изменении их положения, а в остальное время статическую нагрузку воспринимает винт, тогда как в гидравлических толкателях все элементы системы постоянно находятся под большим давлением, что значительно снижает их ресурс работы. Кроме того, на экскаваторе КТМ-405т применен новый планетарно-дифференциальный редуктор разработки завода, позволяющий получить большие передаточные числа при относительно небольших габаритных размерах и массе. Для обеспечения нормального режима работы данных узлов необходимо обеспечить равномерную подачу смазки на рабочие части этих механизмов. Так, для редуктора необходимо равномерно подвести смазку к каждому

• * Corresponding author E-mail address: dimkadim@yandex.ru

подшипниковому узлу сателлитов. Для этого следует произвести расчет распределяющих конструкций.

Для расчетов использовали комплекс «σFlow» – универсальный CFD (Computational Fluid Dynamics) пакет программ [1] и oNet - программа сетевого моделирования процессов гидрогазодинамики [2].

Математическая модель

В качестве математической модели для описания течения жидкости в сети была принята модель установившегося ламинарного течения несжимаемой жидкости. Для представления системы трубопроводов используется ориентированный граф, матрица связей которого представляется в виде

• 1,    если l е О , ⁱ

^V« = П если l ^е I i ,

0, иначе, где l е Oi - множество труб, исходящих из i-го узла, l е I, - множество труб, входящих в i-й узел. Используя матрицу связей, задачу потокораспределения в сети можно свести к сочетанию закона сохранения массы в узле и закона падения давления в трубе:

Z ^V U = q , - ^е N,

i

IV-P^. (u,), l е U.

Здесь u_l – вычисляемый несущий поток в трубе, q_i – источник в узле, p_i – потенциал в узле, а h l ( и) - закон падения давления в трубе. Для ламинарного течения в гидравлических сетях закон падения давления описывается уравнением Дарси-Вейсбаха:

h , ( и , ) =

8 ■ 5

п² ■р- d ⁴

128 ■ v ■ l

■ U l² +--4-- U l ,

d4 ■ п

где Z - местное гидравлическое сопротивление, l - длина трубы, d - диаметр трубы, р - плотность масла, u – массовый расход масла в трубе, ν – вязкость масла. Для определения местных сопротивлений ряда элементов сети использовали эмпирические формулы [3]. Однако не для всех элементов имеются такие эмпирические данные, поэтому для их определения использовалось пространственное моделирование. В качестве математической модели для описания пространственного течения в поворотном штуцере была принята модель несжимаемой жидкости. В рассматриваемой задаче течение жидкости считается установившимся. Поэтому все уравнения записываются в стационарной постановке. Математическая модель включает уравнение неразрывности и уравнения баланса количества движения. В общем виде уравнение переноса для скалярных величин, перечисленных выше, записывается следующим образом:

5^ + V( р v ■ ф) = 7(г^ ф) + Qф, ф = {1, и, V, w}, где φ – скалярная величина, в данном случае компоненты вектора скорости, Γ – эффективный коэффициент диффузионного переноса, Qφ – источниковый член.

Постановка задачи (задача смазки)

На КЗТМ при создании экскаватора КТ-405т был спроектирован дифференциальнопланетарный двухступенчатый редуктор с приводом через корону. Для обеспечения смазки подшипников сателлитов неподвижного водила и подшипников приводных вал-шестерен была спроектирована магистраль системы смазки (рис. 1.) Кольцевой маслопровод осуществляет подачу смазки в подшипники сателлитов, а боковые отводки осуществляют подачу масла в подшипники приводных шестерен сателлитов.

Для обеспечения нормальной работы редуктора при номинальном режиме работы необходимо пропускать через него масла 50 л/мин.

В связи со сложной конфигурацией системы была поставлена задача выравнивания расходов из выходных отверстий путем перекрытия последних шайбами с отверстиями разного диаметра.

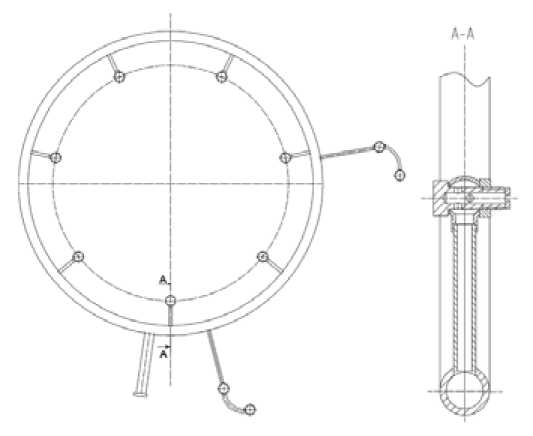
Рис. 1. Чертеж системы смазки редуктора

Пространственное моделирование штуцера

При определении местного сопротивления поворотного штуцера было использовано пространственное моделирование. Для этого была создана модель штуцера (рис. 2) и проведена серия расчетов. Расход масла через штуцер задавался 2,27; 4,55; 9,09; 13,64 л/мин. На рис. 3 отражены результаты расчета при требуемом расходе в виде полей скоростей и давления.

Результаты расчетов в виде графика зависимости перепада давления от расхода приведены на рис. 4. Крестиками показаны данные 3-мерных расчетов, кривой – значение аппроксимирующей функции. В результате анализа определили, что в сетевой модели штуцер можно описать в виде трубки диаметром 6 мм, длиной 18,5 мм, с коэффициентом местного сопротивления 3,0.

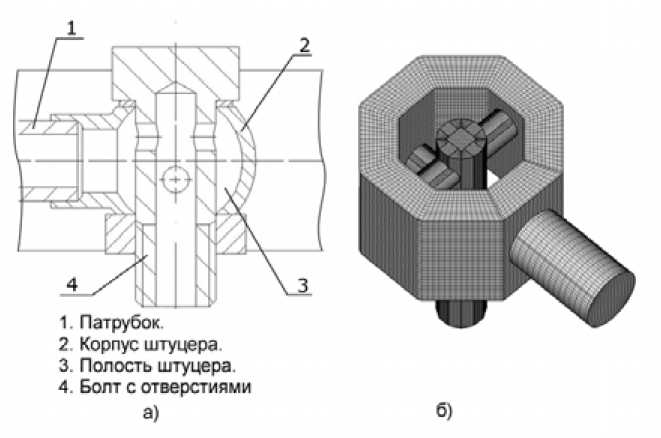
Рис. 2. Модель поворотного штуцера: а – эскиз, б – расчетная сетка

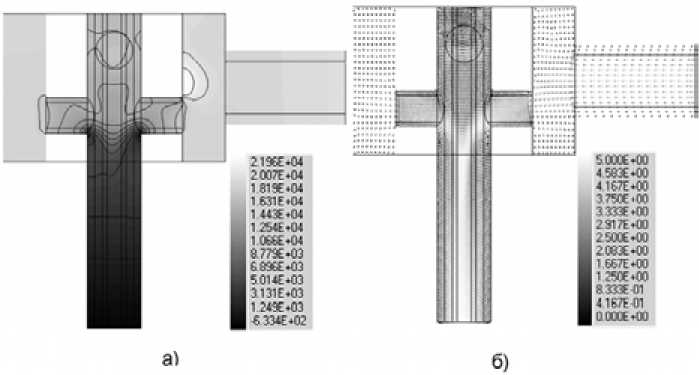
Рис. 3. Результаты расчета модели в осевом сечении поворотного штуцера: а – поле давления, Па; б – поле скоростей, м/с

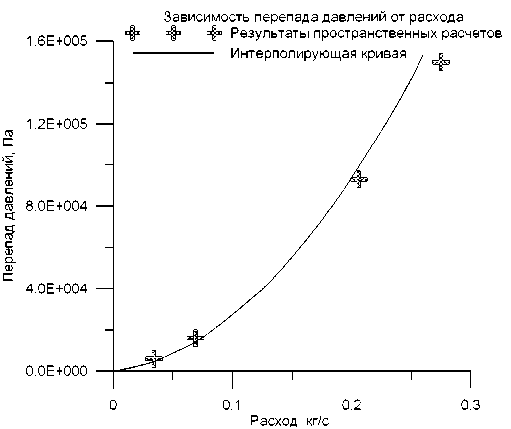
Рис. 4. Зависимость перепада давления в поворотном штуцере от расхода

Пространственное моделирование тройников

Эмпирические формулы и таблицы [3] позволяют определить местное сопротивление участков тройников для турбулентного режима течения. Однако для рассматриваемой задачи течение масла ламинарное, поэтому для определения гидравлического сопротивления тройников была использована 3D модель тройника (рис. 5). Определяли перепады давления на проходном и боковом ответвлениях тройника для каждого из девяти тройников на главной магистрали. При постановке задачи расход в боковом ответвлении всех тройников, за исключением 2-го и 4-го, принимался равным необходимому для обеспечения смазки, во 2-м и 4-м – расход был удвоен. Расходы в сборных и прямых ветвях тройников определяли по балансовым соотношениям для сетевой модели при равных расходах через все выпускные отверстия.

На рис. 6 показаны поля скоростей и давлений для тройника 3. Основными данными в этом случае был перепад давления между сборной и боковой ветвями тройника, а также сборной и прямой. По результатам моделирования было установлено, что перепад давления между сборной и боковой трубами для всех вариантов тройника был приблизительно равен 9700 Па. Перепад давления между сборной и прямой трубой оказался существенно меньше. При дальнейшем исследовании на сетевой модели было установлено, что сопротивление прямой трубы не оказывает значительного влияния на результирующие расходы.

Вышесказанное позволило ограничиться рассмотрением перепада давления между сборными и боковыми трубами для 3, 4 и 7-го тройников. Для них была выполнена серия расчетов, в которой варьировался расход в боковой трубе, расходы в сборной и боковой трубах при этом пропорционально масштабировались.

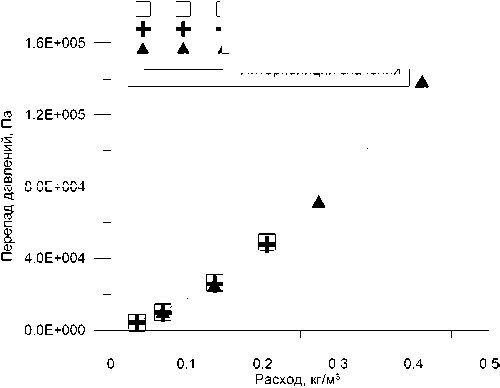
В результате проведенного исследования установили, что для тройника 3 боковую трубу в сетевой модели можно описать как трубу диаметром 8 мм, длиной 100 мм и коэффициентом местного сопротивления 2,4. Сравнивая получившуюся зависимость для остальных тройников (рис. 7), приходим к выводу, что все тройники главной магистрали имеют примерно близкие значения гидравлического сопротивления.

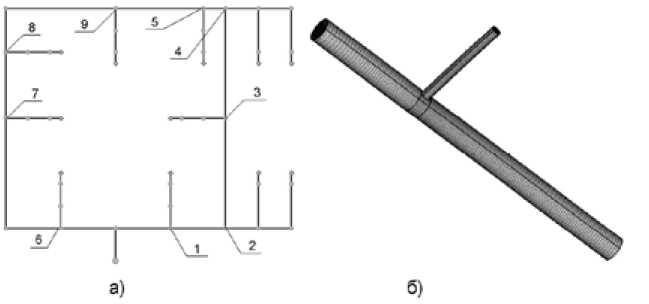
Рис. 5 Моделирование тройников: а – номера тройников, б – расчетная сетка

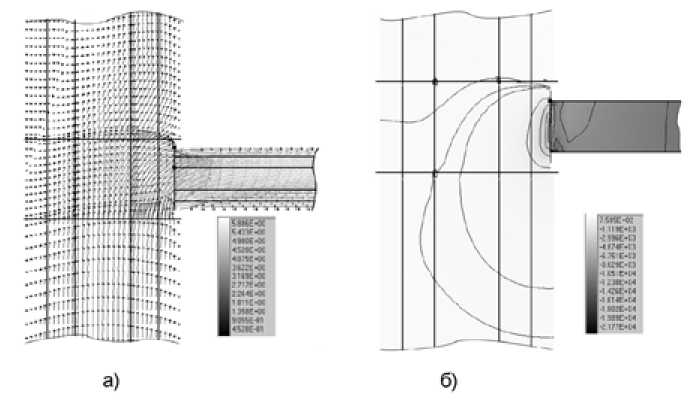
Рис. 6. Поля скоростей и давления в осевом сечении тройника 3: а – вектора поля скоростей, б давления

поле

Перепад давлений в тройниках Первый тройник

+ Третий тройник

А Второй тройник Интерполяция значений

8.0Е+004

Рис. 7. Зависимости перепадов давлений в боковом ответвлении тройника от расходов

Сетевое моделирование

Полученные в результате 3-мерных расчетов сопротивления и длины элементов использовались в качестве параметров сетевой модели системы смазки редуктора (рис. 8). Результаты расчета сетевой модели системы представлены на рис. 9.

По результатам расчета видно, что подача масла в сателлиты (отверстия 3-9) осуществляется равномерно. Однако подача масла через отверстия приводных шестерен (отверстия 1,2,10,11) существенно меньше. Это связано с тем, что из центральных штуцеров смазка подается непосредственно в подшипники сателлитов, а смазка для приводных шестерен должна еще пройти через конструктивные элементы корпуса редуктора хода. Такой ситуации можно было избежать, если бы диаметр дополнительных труб был выбран в 1,5 раза большим.

Для существующей конструкции была выполнена серия расчетов с целью определения необходимых диаметров регулирующих шайб, которые бы обеспечили необходимый уровень расхода в узлах системы смазки (рис. 6). Для выравнивания расхода масла в системе его значения для отверстий приводных шестерен задавали на 20 % большими по сравнению с расходами

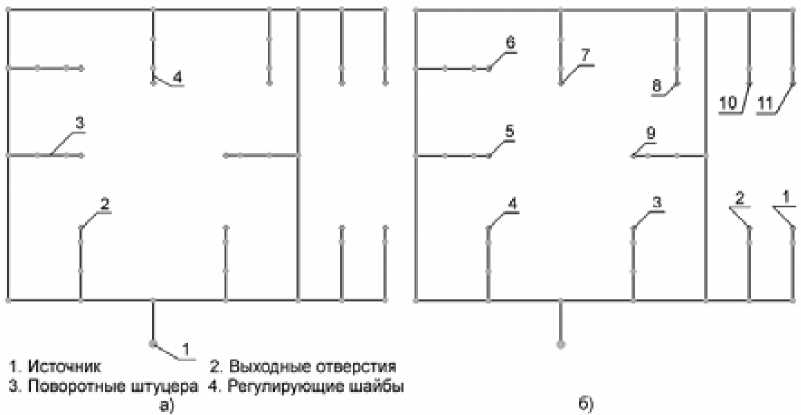
Рис. 8. Сетевая модель магистрали смазки редуктора: а – сетевая модель; б – номера отверстий системы смазки (3-9 – сателлиты, 1,2,10,11 – приводные шестерни)

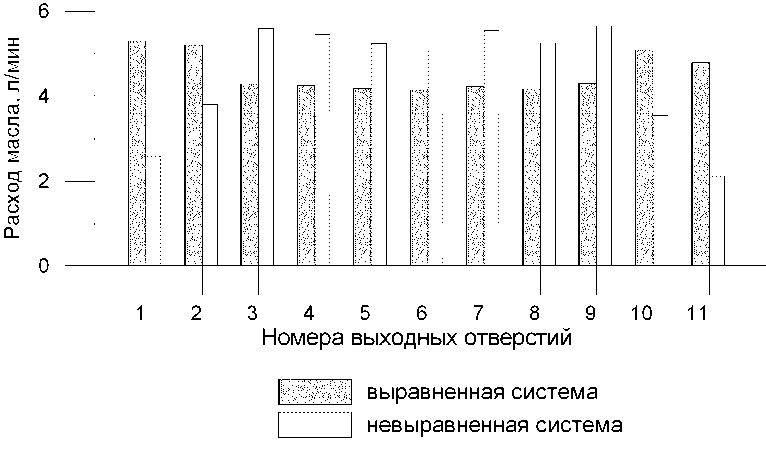
Рис. 9. Распределение расходов в выходных отверстиях в отверстиях сателлитов. Требование такого расхода обусловлено более высоким тепловыделением шестерен. Полученные в результате коэффициенты местного сопротивления и, как следствие, диаметры шайб позволяют обеспечить нужные значения расходов.

Выводы

Построена сетевая модель системы смазки редуктора хода экскаватора КТМ405т, выполнено трехмерное моделирование поворотного штуцера. Определены зависимости, описывающие движение масла в поворотном штуцере. Полученные данные использовали для сетевого моделирования конструкции системы смазки редуктора хода экскаватора КТМ-405 т.