Моделирование скоростного упрочнения полимерного композитного материала при нагружении вдоль направления армирования

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2024PNRPU MECHANICS BULLETIN

В последние годы проявляется все больший интерес к использованию композитных материалов в конструкциях, где в экстремальных ситуациях возможно высокоскоростное деформирование. Примерами таких ситуаций могут быть определенные аварийные случаи с сосудами высокого давления, аварийная посадка самолетов, работающих на сниженном топливе [1–4].

Кроме того, существует потребность моделирования пробивания композитной брони, где деформации композитного материала также предельно высоки [5].

Направление работ по экспериментальному исследованию высокоскоростных деформационных характеристик композитных материалов в основном связана с использованием методов на основе метода разрезного стержня Кольского. Многие эффекты скоростного упрочнения показаны, но для относительно небольших скоростей деформирования, что во многом связано с малыми размерами стандартных образцов [6–11].

Другая актуальная тема, где вопросы скоростного деформирования актуальны, это низкоскоростной удар по композиту. При эксплуатации композитных конструкций одним из наиболее уязвимых мест является случайное повреждение ударом (падение инструмента). Притом, что скорости удара низкие, локальные деформации могут быть высоки. В этой области много работ по моделированию и возможность моделировать скоростное упрочнения композитного материала наиболее востребована [12–16]. Во многих работах по моделирова- нию используется понятие поврежденности [17; 18]. В данной работе мы будем использовать именно такой подход, и в качестве параметра повреждения рассматривается степень изменения жесткости материала. Пластическое деформирование предполагается незначительным и не используется в предложенных соотношениях. После любого воздействия материал разгружается в нулевые деформации, хотя при высокой степени повре-жденности с очень низким значением модуля упругости.

За основу взята модель, предложенная коллективом авторов в работах [19–21], при этом в работе [22] представлена модель именно для скоростного разрушения. Основная цель работы – использовать соотношения из работы [22] для нагружения однонаправленного композита вдоль армирования в более высоком диапазоне скоростей деформирования. В качестве исследуемого материала используется композит на основе связующего фирмы Huntsman LY516 и волокна Т700. Образцы были созданы технологией намотки с процентным содержанием волокна 50 %.

1.    Экспериментальное исследование

Исследования динамического деформирования и разрушения композитного материала проводилось с использованием классического варианта метода Кольского в условиях сжатия. Для возможности нагрузить образец более высокими скоростями деформирования использовалась специальная геометрия образцов и соответствующая оснастка (рис. 1, 2).

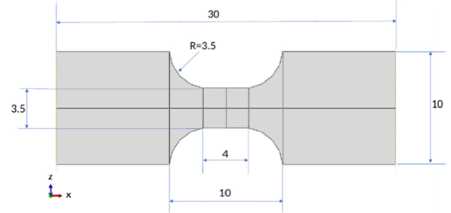
Рис. 1. Схема образца

Fig. 1. Scheme of the sample

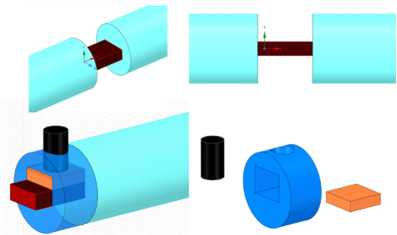
Рис. 2. Схема оснастки

Fig. 2. Scheme of fixture

На рис. 3 показаны результаты высокоскоростной фотосъемки во время деформирования образца. Примеры полученных временных зависимостей напряжений показаны на рис. 4.

Рис. 3. Процесс деформирования и разрешения образца в оснастке

Fig. 3. The process of deformation and resolution of the sample in the fixture

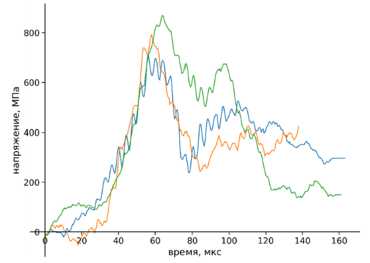
Рис. 4. Временные зависимости напряжений, полученные в экспериментах

Fig. 4. Time dependences of stresses obtained in experiments

2.    Описание модели Для построения модели будем использовать подход, предложенный в работе [22]. Определяющие соотноше- ния [V приведены в уравнениях (1). " 1        V2V21     V2V3i      0        0        0 " W1 E11      E 22       E33 W2V12      1        W2V 2     0        0        0 E11     ^2 E22      E33 fa111 a,2 , (1) [°33. 012 013 °' , е22 *' Y12 Y13 7- W Av     W2V23      1        0       0       0 =    E11       E 22    W2E33 0     0     0   ——  0    0 w2 G12 0     0     0    0  ——  0 W2 G13 0     0     0    0    0  —— _                                                    W2 G23 _

Видно, что соотношения (1) являются стандартной связью напряжений и деформаций для линейно упругого ортотропного тела, в которые входят множители ψ i . Упомянутые множители являются параметрами поврежден-ности и снижают жесткость материала в процессе его деградации при деформировании. При этом множитель ψ 1 отвечает за разрушение волокна, а множитель ψ 2 связан с разрушением матрицы композита. В начале моделирования оба множителя равны единице ψ i =1, что соответствует идеальному неповрежденному материалу. Нулевые значения соответствуют полному разрушению соответствующей составляющей.

В данной работе нас интересует случай одноосного сжатия вдоль направления армирования, что сводит соотношения (1) к формуле (2):

ε ₁₁ =σ ₁₁/ ψ ₁ E ₁₁. (2)

Далее необходимо задать закон деградации материала, то есть закон изменения параметра ψ 1 . Для этого выберем соотношения, которые реализуют следующую схему деформирования, представленную на рис. 5.

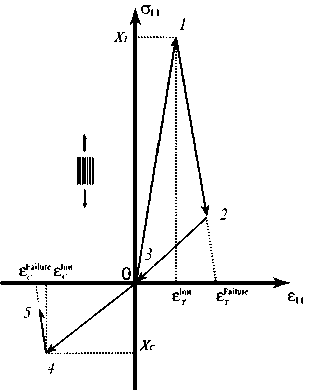
Рис. 5. Схема продольного нагружения

Fig. 5. The scheme of longitudinal loading

Любая диаграмма нагружения при разгрузке возвращается в ноль, на участках 1–2 в случае растяжения и 4– 5 в случае сжатия происходит рост параметра повре-жденности ψ 1 , при этом диаграмма линейно падает вниз. Параметры X T и X C отвечают напряжениям разрушения вдоль армирования в случае растяжения и сжатия соответственно. Параметры ε T ^Init, ε T ^Failure, ε С ^Init, ε С ^Failure отвечают деформациям начала разрушения и полного разрушения для растяжения и сжатия соответственно.

В случае активного процесса разрушения напряжения находятся на поверхности разрушения, которая, в свою очередь, зависит от параметров поврежденности. В случае разрушения при сжатии можно записать следующее выражение:

σ ₁₁ = X _С ( ψ ₁). (3)

Диаграмму, представленную на рис. 5, можно реализовать, используя зависимость для X C в следующем виде:

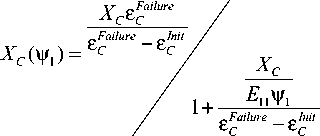
Здесь X C и E 11 – начальные параметры прочности и жесткости, до начала процесса деградации или изменения параметра ψ 1 . Влияние скорости деформирования согласно [22] можно учесть, вводя в зависимость параметра прочности X C параметр скорости поврежденности й 1 , что в общем случае приводит к зависимости прочностной характеристики от двух параметров, а условие активного разрушения в случае одноосного сжатия может быть сформулировано следующим образом:

о_п = X С (у_р й 1 ). (5)

При этом статическую часть зависимости можно рассмотреть в виде (4), а динамическую часть учесть, как специальный множитель по аналогии с работами Джонсона Кука. В качестве динамического множителя предлагается использовать степенную зависимость от скорости роста повреждения, что окончательно приводит к выражению для условия прочности:

X С ( й 1 , й 1 ) = xC (vD X c" ( й 1 ) =

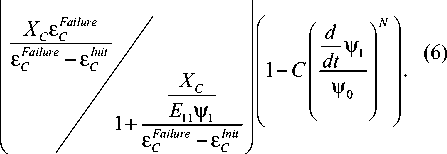
Параметры C, N, ψ0 – константы, определяемые экспериментально. Предполагается, что если скорость повреждений й 1 оказывается меньше у0, то XDynn (й 1) = 1 и анализ происходит под влиянием только статической составляющей XCSt(ψ1).

3.    Получение параметровна основе экспериментальных данных

Используя соотношения (5) совместно с (6), условие активного разрушения можно записать в следующем виде:

о_п =й 1 E_n£ ii = X с ( й_Р й 1 ).           (7)

При этом предположим, что скорость деформирования постоянная Ё_п = v , тогда:

й Е_п vt = X с ( й 1 , \й 1 ).                (8)

Соотношение (8) является обыкновенным дифференциальным уравнением относительно параметра ψ 1 , которое можно решать самыми стандартными способами. Окончательно имеем:

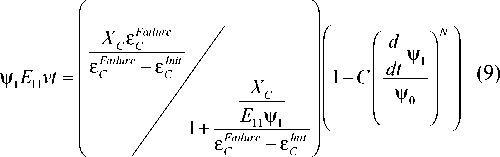
при начальных условиях ψ 1 (ε С^Init / v )=1, так как вначале материал не повреждён.

Уравнения (8) и (9) по форме схожи с моделями, предлагаемыми для параметров поврежденности основателями данного направления исследований – Л.М. Качановым [23] и Ю.Н. Работновым [24], при этом материал находится не в условиях ползучести, а претерпевает высокоскоростное деформирование.

Уравнение (9) является основой для получения констант C , N , ψ 0 из экспериментальных данных.

Типовое решение уравнения (9) показано на рис. 6.

В табл. 1 приведены упругие и прочностные характеристики материала в случае одноосного сжатия, полученные экспериментально.

На рис. 7 показаны диаграммы напряжений и деформаций, полученные с использованием модели, соответствующие константы приведены в табл. 2. На рис. 8 показаны экспериментально полученные максимумы напряжений совместно с предсказаниями модели. В табл. 2 приведены константы, использованные для получения диаграмм.

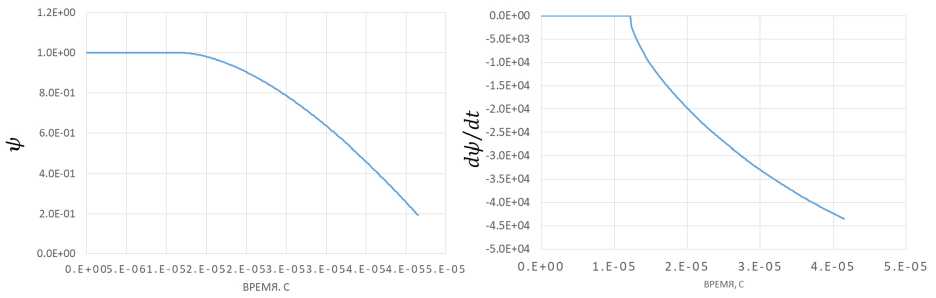
Рис. 6. Зависимость параметра повреждения и скорости повреждения от времени

Fig. 6. Dependence of the damage parameter and the damage rate on time

Таблица 1

Механические характеристики материала в условиях статики

Mechanical characteristics of the material under static conditions

Table 1

E 11 , МПа	Xc , МПа	ε С Init	ε С Failure
115000	600	0,0052	0,06

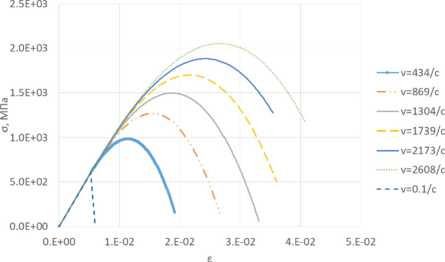
Рис. 7. Диаграммы нагружения материала при разных скоростях деформирования

• Fig. 7.    Diagrams of material loading at different deformation rates

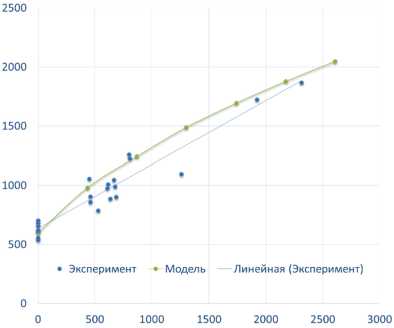
Рис. 8. Максимумы напряжений достигнутые при различных скоростях деформирования

• Fig. 8.    Maximum stress at different deformation rates

4.    Анализ результатов

Таблица 2

Данные для модели скоростного упрочнения

Table 2

Data for the model of rate-dependent hardening

С	N	ψ 0
2.30E-07	1,5	0,2e-4

Стоит отметить, что в моделировании неявно предполагалось постоянство упругих характеристик. Проблема состоит в отсутствии надежной методики измерения жесткости при рассматриваемых скоростях деформирования. С другой стороны, правомерность такого предположения подтверждается незначительным изменениями модуля (+1,2 %) при продольном деформировании до 100 с-1 в работе [6]. Также можно воспользоваться температурной аналогией [25] и рассмотреть изменение продольного модуля при сверхнизких температурах [26], которые также дают небольшое изменение модуля (< 15 %).

Образцы были получены методом намотки, что изначально вносит некоторый дефект и определенную кривизну в их форму. Этот факт существенно влияет именно на свойства при сжатии образца. Тем не менее статическую прочность можно скорректировать по результатам других испытаний, а вот динамическая составляющая определена корректно, так как она по сути просто масштабирует статическое поведение.

Заключение

В работе представлен подход, позволяющий моделировать разрушение композитного материала при высоких скоростях деформирования. Использован материал, полученный методом намотки. Показано, что предложенный подход позволяет моделировать разрушение в широком диапазоне скоростей деформирования, начиная от статического нагружения до 2500 обратных секунд. Модель ограничена процессом нагружения в условиях одноосного сжатия. С учетом рассеяния экспери- ментальных данных результаты моделирования имеют хорошее соответствие.

Для моделирования реальных конструкций в будущих работах данного направления необходимо