Моделирование слойной структуры бесконечных групп

Введение. Ранее С. Н. Черниковым исследовались бесконечные слойно конечные группы, которые впервые появились в его работах сначала без названия, а затем в его последующих публикациях за ними закрепилось название слойно конечных групп. Мы будем исследовать мощности слоев в некоторых слойно конечных группах. Слоем называется множество всех элементов группы одного порядка.

Наиболее интенсивные исследования свойств слойно конечных групп проводили в 1940-х – 1950-х годах С. Н. Черников, Р. Бэр, X. X. Мухаммеджан. К концу 1950-х годов основные свойства были уже получены и опубликованы в различных журналах. В таком виде они оставались до 1980 г., когда появилась монография С. Н. Черникова [1]. Свойства слойно конечных и почти слойно конечных групп рассматриваются в работах [2–13].

Если все слои элементов в группе конечны, то для такой группы возможно функциональное описание мощности слоев.

В статье дается функциональное описание для некоторых слойно конечных групп. Показано, что поддаются визуализации примарные слойно конечные группы и слойно конечные группы в случае двух простых делителей порядков элементов группы. В случае двух простых делителей проведена визуализация при помощи поверхностей в трехмерном пространстве. Для большего числа простых делителей предложен подход при помощи подгруппового анализа. Моделирование слоев в группах при помощи слойных графов можно найти в работах [14; 15].

Основной результат. Сначала в качестве примера рассмотрим некоторые слойно конечные p -группы и их конечные расширения.

Найдем мощности слоев группы C „ , где p - про стое число. В группе Cp„ один элемент порядка 1, p -1 элемент порядка p, p2 - p элементов порядка p2, _, pn - pn-1 элементов порядка pn,..

График функции мощности слоев группы C p „ представляет собой точки, лежащие на прямой с уравнением:

где m – число квазициклических групп в прямом разложении группы

Cx^xxC ..

p             p ,

m

Изобразим это на графике (рис. 2).

При моделировании картины, представляющей собой мощности слоев группы С „ x C k , будем иметь дело с двумя функциями, содержащими значения, соответствующие мощностям слоев, которые имеют вид

2p -1                 к y = x ---2—, при p < x < p , p2

y = x ( p k - p^{k -1} ) , при x >  p^k .

Изобразим это на графике (рис. 3).

График функции мощности слоев группы

k

С x C , , начиная со значения p до значения p , p ”     p представляет собой точки, лежащие на параболе, k+1        k+m и с p до p – точки, лежащие на прямой.

Рассмотрим группу Cp„ x Cq„ , где p < q . График функции мощности слоев группы Cp„ x Cq„ (рис. 4) представляет собой точки, лежащие на сегменте поверхности второго порядка с абсциссами p, p2, …, pn, …, и ординатами q, q2, …, qn, …, задаваемой уравнением p-1 q-1

z = x----y ----, x >  p , y >  q .

pq

Рассмотрим группы с числом простых делителей элементов, больше двух. Для примера, рассмотрим группу C _r x С 3 „ x C 3 „ x C 5 „ . Изобразить ее мощности слоев сложно, для этого удобно работать в четырехмерном пространстве. Будем работать с подгруппами, отвечающими паре простых чисел. Например, 2, 3, изображая мощности части слоев, отвечающие номерам слоев, делящихся на 2 и 3. Получается подгруппа C 2 „ x С 3 „ x C ₃ . .

Функция мощности слоев этой подгруппы будет иметь вид p-1 y = x- ,X > p.

p

Изобразим это на графике (рис. 1).

В случае большего числа прямых множителей график функции мощности слоев группы C p x ^x C p ” представляет собой точки, лежащие

z =

4 xy ² 9

, x >  p , y >  q .

m на кривой с уравнением

y = X

^m m p

^^^^^^в

pm

-, x > p,

Слойная картина в этом случае будет иметь вид, представленный на рис. 5.

Видно, что полученная иллюстрация представляет точки с абсциссами 2, 22, 23, … и ординатами 3, 32, 33, …, лежащие на сегменте поверхности.

Еще рассмотрим пару простых чисел 3, 5, изображая мощности части слоев, отвечающие номерам слоев, делящихся на 3 и 5. Получается подгруппа C 3 „ x С 3 „ x С 5 „ .

Функция мощности слоев этой подгруппы будет иметь вид

32 x ² y 45

, x >  p , y >  q.

Слойная картина в этом случае показана на рис. 6.

Видно, что полученная иллюстрация представляет точки с абсциссами 3, 3², 3³, … и ординатами 5, 5², 5³, …, лежащие на сегменте поверхности .

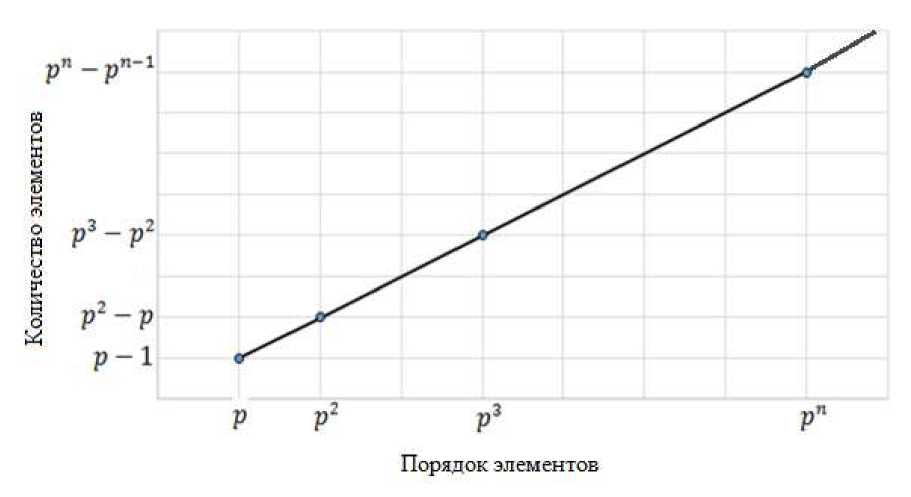
Рис. 1. График функции мощности слоев группы

C p

Fig. 1. Graph of capacity function of layers of the group C p „

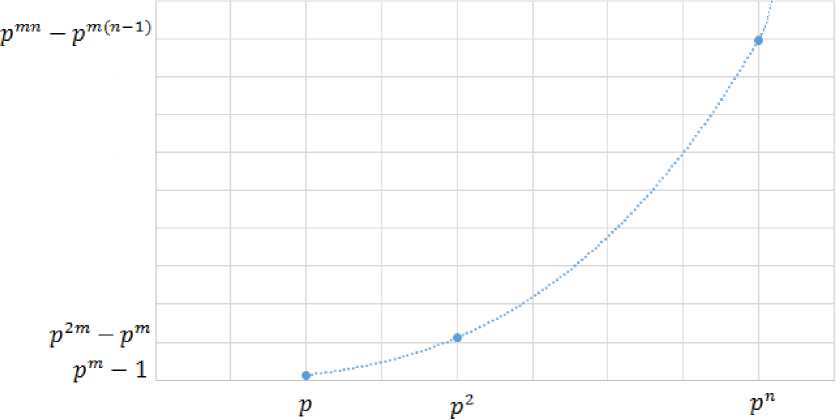
Порядок элементов

Рис. 2. График функции мощности слоев группы C p „ x ■ x C p „

m

Fig. 2. Graph of capacity function of layers of the group C p „ x • • ■ x C p „

m

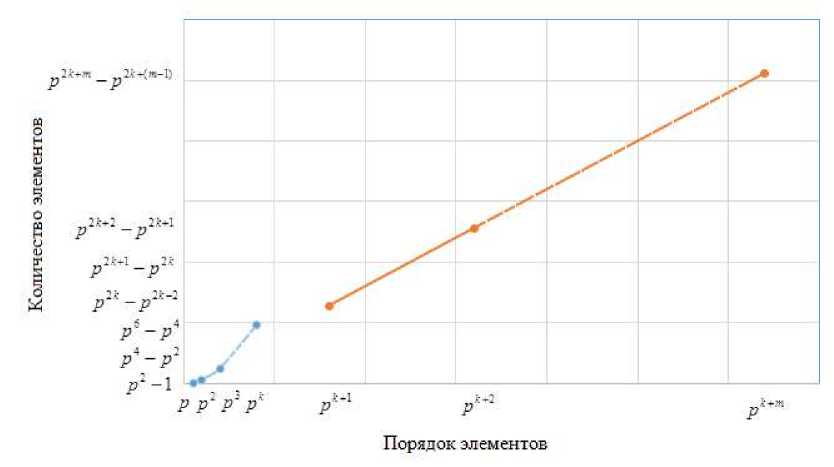
Рис. 3. Слойная картина группы С х С p -     p

Fig. 3. A layered picture of the group

^С р -^{х C} p k

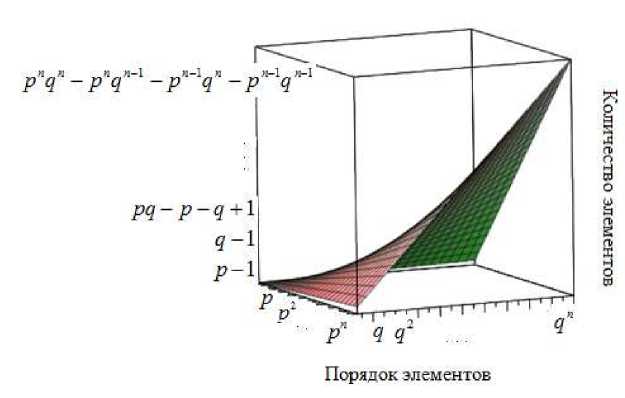
Рис. 4. Слойная картина группы С х С p ”      q ”

Fig. 4. A layered picture of the group С х С p ^-      q ”

Осталось рассмотреть случай пары чисел 2 и 5.

Этому случаю соответствует подгруппа С 2 „ х С 5 „ .

Функция мощности слоев этой группы будет иметь вид

2xy

z = —, x ^ p, У ^ q.

Слойная картина в этом случае будет иметь вид, представленный на рис. 7.

Видно, что полученная иллюстрация представляет точки с абсциссами 2, 22, 23, … и ординатами 5,

• 5², 5³, …, лежащие на сегменте поверхности второго порядка.

Рассматривая эти три подгруппы, можно представить себе, как выглядит слойная картина группы С 2 - х с ₃ - х С ₃ - х С 5 - .

Аналогично рассмотренному примеру можем рассматривать произвольную полную слойно конечную группу (так как полная слойно конечная группа является прямым произведением конечного числа квази-циклических групп) с числом делителей порядков элементов больше двух.

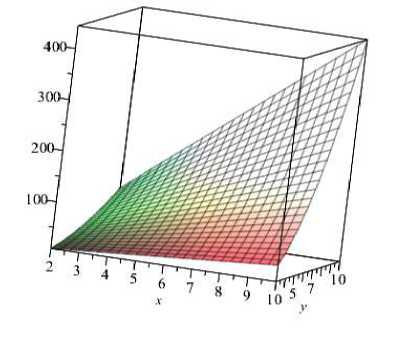
Рис. 5. Слойная картина подгруппы C X С 33 _/ X C _з „

Fig. 5. A layered picture of the group C ₂ „ X С 3 „ X C 3 „

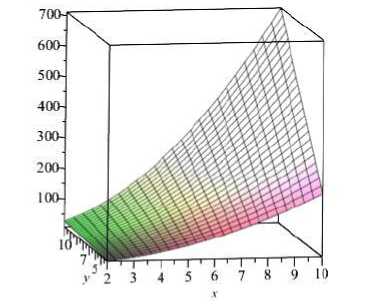
Рис. 6. Слойная картина подгруппы C 3 „ X С 3 „ X С

Fig. 6. A layered picture of the group C 3 „ X С 3 „ X С 5 „

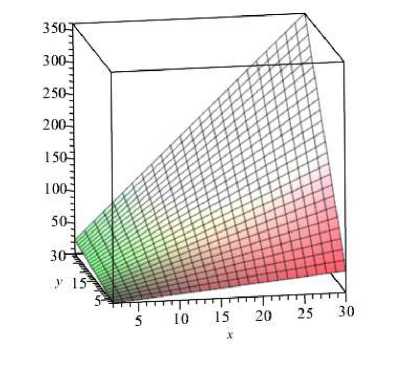
Рис. 7. Слойная картина подгруппы C 2 „ X С _; „

Fig. 7. A layered picture of the group C _X С 5 _/

Заключение. В статье найдены функции, по которым вычисляются мощности слоев некоторых полных слойно конечных групп и их конечных расширений, продемонстрированы их графические представления. Построены графики для функций, описывающих мощности слоев примарных слойно конечных групп. В случае двух простых делителей порядков элементов группы проведена визуализация при помощи поверхностей в трехмерном пространстве. Для большего числа простых делителей предложен подход при помощи подгруппового анализа.