Моделирование спектральных функций осциллятора с кубической нелинейностью возвращающей силы

В работах [1, 2] авторами показано, что диэлектрические спектры релаксационной поляризации могут быть описаны с помощью модели заторможенного линейного осциллятора. Поскольку реальные релаксационные спектры в большинстве случаев удовлетворительно или плохо совпадают со спектром линейного осциллятора, можно предположить, что для этой цели может быть применена модель заторможенного нелинейного осциллятора. В настоящее время теория нелинейных колебаний разработана достаточно хорошо [3, 4]. Найдены методы решения нелинейных уравнений, различные нелинейные осцилляторы, получены решения, позволяющие получить спектры колебаний. Но теория заторможенных нелинейных осцилляторов сейчас разработана очень слабо.

Рассмотрим классический осциллятор, состоящий из двух пружин и шарика на стержне [5], колеблющийся с достаточно большой амплитудой, настолько, что упругая возвращающая сила становится нелинейной.

Уравнение, описывающее движение линейного осциллятора имеет следующий вид [5]:

d 2 xdx

—— + 2^™ + ®o x = 0, dt2

где x - координата осциллятора, р - коэффициент затухания, ю₀ - собственная частота колебаний, m – масса. Собственная частота определяется выражением: to 0 = k / m , здесь к - постоянный коэффициент, определяемый упругими свойствами пружины. Для нелинейных колебаний коэффициент k будет неизвестной функцией координаты, разложим эту функцию в ряд:

k ( x ) = k о + k i x + k 2 x ² + k 3 x ³ + ... (2)

упругая сила равна нулю, второй в силу симмет- рии задачи, поскольку квазиупругая сила должна менять знак при смене знака x. Пренебрегая членами ряда степени выше третьей, получаем:

k ( x ) * k i x + k 3 x ³ . (3)

Отсюда мы можем записать уравнение осциллятора с кубической квазиупругой силой, или осциллятора Дуффинга [3]:

d 2 x       dx 2       2 3

—Y ^{+ 2 р} , ⁺ ® 01 ^{x +} ® 03 ^x = ⁰ , (4)

dt 2        dt здесь o>01 - собственная частота колебаний линейного осциллятора, m03=k3/m - коэффициент, который можно рассматривать как собственную частоту осциллятора с чисто кубической упругой силой. Выражение (3) определяет вид потенциальной ямы, в которой колеблется рассматриваемый осциллятор:

U ( x ) = a i x ² + a 3 x ⁴ . (5)

где а₁ и а₂ некоторые константы.

Поскольку нас интересует применение этой модели для описания релаксационной поляризации, нам необходимо рассмотреть заторможенный режим колебаний. Так же как и в работах [1, 2], отбрасываем первое инерционное слагаемое в уравнении (4), поскольку инерция становится пренеб- режимой по сравнению с силой трения и получа- ем укороченное уравнение Дуффинга:

dx

2p--+ to01 x + to02 x = 0

dt

В работе [6] показано, что для линейного осциллятора укороченное уравнение точно описывает заторможенные колебания при условии р>5ю₀ . Пока мы не можем определить аналогичное условие для нелинейного осциллятора, потому будем считать, что в этом случае с достаточной точностью выполняется приведённое выше условие.

Уравнение (5) может быть представлено в виде уравнения Бернулли [7], интегрирование которого [3] даёт:

x (1) = I 1=

® 2

Ce 211 г + _J)3 ,(6)

V где г = 2PI ®01 - постоянная времени линейного осциллятора [2], t - время, С=1Ix0 + ®03I®01 – постоянная интегрирования, определяемая начальной амплитудой х0. Очевидно, что при ®03=0 решение (6) переходит в функцию

x ( 1 ) = Ce ^{- 1 1 т} ,                (7)

описывающую свободное движение линейного осциллятора [2, 5].

Поскольку нашей задачей является применение модели нелинейного осциллятора к описанию релаксационной поляризации, то нам необходимо найти зависимость амплитуды вынужденных колебаний осциллятора от частоты внешнего поля A ( ® ) или спектральную функцию (рис. 1). Эту функцию мы можем найти, применив преобразование Фурье к решению (6) [8]. Преобразование Фурье даёт интеграл

~ m

A (®) = J .dl

a

0 Ce211 т - «*23    ,(8)

V ®oi здесь нижний предел интегрирования взят равным нулю, поскольку время не может быть отрицательным. Этот интеграл мы взять не смогли, поэтому далее применили цифровое интегрирование. Для интегрирования в среде MathCAD выражение (8) было преобразовано к виду:

(           ₂ ^ - 1I2

~/..\     - i ® 1    2 11 г ® 3

A ⁽ « ) = J ^{e     Ce}-- 03       d¹ . (9)

0 V         «01)

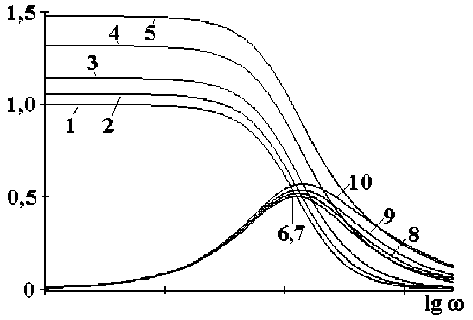
Рис. 1. Действительная (1-5) и мнимая (6-10) части спектральной функции нелинейного осциллятора для различных значений параметра а : 1, 5 – а = 0; 2, 6 – а = 0,3; 3, 7 – а = 0,6;

4, 8 – а = 0,9; 5, 10 – а = 0,99

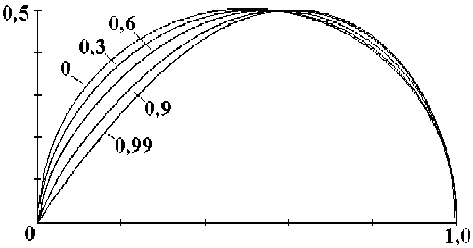
Рис. 2. Фазочастотные характеристики для спектральной функции заторможенного осциллятора Дуффинга для различных значений параметра а .

Цифрами на графиках обозначены значения а

Результаты интегрирования показаны на рис. 2. Графики построены в полулогарифмическом масштабе, это форма представления принята в физике диэлектриков. Кривые нормированы на амплитудное значение действительной части спектра линейного осциллятора ( а= 0). Как видно из рисунка, действительная и мнимая части спектральной функции достаточно слабо зави-

« 03

сят от соотношения a = —/С . С ростом а «01 / происходит незначительное уширение пиков мнимой части, действительная часть становится более пологой и происходит незначительное увеличение амплитуды. Ещё одно отличие спектров осциллятора Дуффинга от линейных спектров состоит в том, амплитуда пиков мнимой части меньше полувысоты действительной части и координата полувысоты не совпадает с максимумом пика. С ростом а отличия нарастают.

Для того, чтобы выявить различия в форме кривых, в физике диэлектриков применяют диаграммы Коула-Коула (Cole-Cole) [9], или графики построенные в координатах ( ^ '( ® ), ^ "( ® ) ), где ^ '( ® ), ^ "( ® ) - действительная и мнимая части диэлектрической проницаемости. С математической точки зрения эта диаграмма представляет собой годограф вектора с соответствующими координатами, или фазо-частотная характеристика (ФЧХ), если использовать термины, принятые в автоматике. Мы будем использовать последнее название, как более удобное. На рис. 3 построены ФЧХ нормированной по амплитуде спектральной функции осциллятора Дуффинга для различных значений отношения а . Из рис. 3 следует, что при а=0 ФЧХ представляет собой правильный полукруг, что соответствует ФЧХ спектральной функции линейного заторможенного осциллятора [6]:

• ~ , х     A 0      Д 1       .гот )

A L ⁽ ® ) =   — = A 0I---- ГТ^{- z} ----ГТ I, (10)

• ^{1    +} i ®^T     V 1 + ® ² т ²    1 + ® ² т ² )

  

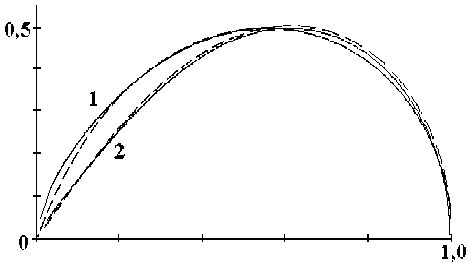
  Рис. 3. Сравнение фазочастотных характеристик для спектральной функции заторможенного осциллятора Дуффинга (сплошная линия) и формулы Дэвидсона-Коула (пунктир): 1 - а = 0,9, у =0,73; 2 - а = 0,99, у =0,5

  
  

здесь А₀ – амплитудный множитель. С ростом а происходит смещение центра тяжести кривых вправо. Наиболее заметные искажения ФЧХ наблюдается при а >  1.

Известно, что такие искажения диаграмм Коула-Коула соответствуют сильной связи релаксирующих частиц в диэлектрике с ближайшим окружением [10]. Подобные диаграммы наблюдаются у некоторых жидкостей, стёкол, полимеров и т.п. Спектральные функции, соответствующие подобным диаграммам описываются эмпирической функцией Коула-Дэвидсона [10]:

~( « ) = 8 _ю +

⁸ s - ⁸ «

(1 + i tor )^{1 - у}

где eo 8s, - высокочастотная (к»к>0) и низкочастотная («<<«>0) части диэлектрической проницаемости, у - параметр релаксации. Можно было бы предположить, что (11) и есть спектральная функция заторможенного осциллятора Дуффинга, но, как показано работе [11], обратное преобразование Лапласа от (11) даёт время-зависимую функцию, которая при t >0 стремится к бесконечности, что физически не обосновано. На рис. 3 показано сравнение ФЧХ для спектральной функции осциллятора Дуффинга и функции (11) Коула-Дэвидсона. Из рисунка видно, что обе функции показывают хорошее, но не полное совпадение. Можно заметить, что явной связи между коэффициентом а и параметром релаксации у нет.

Таким образом, из сравнения спектров заторможенного осциллятора Дуффинга и формул Коула-Дэфидсона следует, что релаксационная поляризация коул-дэвидсоновского типа может быть описана с помощью модели нелинейного заторможенного осциллятора с кубической нелинейностью упругой силы. Отсюда можно сделать вывод, что релаксационная поляризация этого вида вызвана нелинейными колебаниями заряженных частиц в диэлектрике под действием переменного электрического поля. Появление нелинейности вызвано сильным взаимодействием частицы с ближайшим окружением.