Моделирование спектральных характеристик композитов прозрачная матрица-наночастицы со структурой ядро-оболочка
Автор: Каленский Александр Васильевич, Звеков Александр Андреевич, Галкина Елена Владимировна, Нурмухаметов Денис Рамильевич
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 2 т.42, 2018 года.
Бесплатный доступ
В рамках теории Адена - Керкера для концентрических структур ядро-оболочка проведено моделирование оптических свойств композитов прозрачная матрица-наночастицы металлов, покрытых оксидной оболочкой. На примере композитов пентаэритрит тетранитрат - наночастицы Al (Al2O3) показано, что показатели поглощения и рассеяния, коэффициенты коллимированного пропускания, полного отражения и пропускания определяются толщиной образца, радиусом наночастиц, их массовой долей и массовой долей оксида в наночастицах. Предложен способ определения данных параметров при сравнении рассчитанных спектральных зависимостей коэффициентов пропускания и отражения с экспериментальными данными. Наименьшая величина ошибки возникает при определении радиуса наночастицы (порядка 2 - 3 %), а массовая доля наночастиц и массовая доля оксида являются более слабыми параметрами (с точностью определения до 25 %).
Перенос излучения, теория адена - керкера, наночастицы ядро - оболочка, спектры, обработка эксперимента, оптические характеристики
Короткий адрес: https://sciup.org/140228724
IDR: 140228724 | DOI: 10.18287/2412-6179-2018-42-2-254-262
Текст научной статьи Моделирование спектральных характеристик композитов прозрачная матрица-наночастицы со структурой ядро-оболочка
Методы оптической спектроскопии светорассеивающих систем перспективны для использования в медицинской диагностике [1–3], зондировании атмосферы [4], исследовании и анализе материалов [5–7]. Во всех случаях требуется решать обратную задачу с определением актуальных параметров системы на основе сравнения результатов измерения и компьютерного моделирования. Разрабатывается методика извлечения спектральных зависимостей показателей поглощения и рассеяния модельных систем при обработке экспериментальных спектров диффузного поглощения и пропускания коллоидных растворов [8]. В [9, 10] рассмотрено получение спектральной зависимости показателя преломления при обработке спектра ослабления аэрозоля диоксида кремния. Данный подход не только используется в аналитической химии, но и перспективен для исследования материалов со структурно-зависимыми оптическими свойствами.
В [6, 11] проведено измерение коэффициентов полного пропускания и отражения излучения лазерного диода (643 нм) прессованными композитами пентаэритрит тетранитрат – наночастицы алюминия. Предложен способ обработки данных, позволяющий получить комплексный показатель преломления металла [11]. Существенным недостатком методики является игнорирование оксидной плёнки на поверхности наночастицы. В случае наночастиц алюминия данная плёнка образуется во время контролируемого окисления в окончательной стадии электровзрывного синтеза и защищает их от дальнейшего окисления [12, 13]. В [14] исследовались оптические свойства нанесённых на подложку нанодисков алюминия с контролируемой долей оксида. Показано, что увели- чение толщины оксидной плёнки приводит к изменению положения максимума на спектральной зависимости коэффициента эффективности рассеяния. В [15] отмечалось влияние доли оксида в наночастицах алюминия на коэффициент полезного действия кремниевых фотоэлементов с алюминий содержащим антиотражающим покрытием. Наночастицы алюминия рассматриваются как эффективный компонент материалов для плазмоники в ультрафиолетовой и видимой области [16]. Поэтому при рассмотрении оптических свойств композитных материалов, содержащих наночастицы алюминия, оксидную плёнку на их поверхности необходимо учитывать.
Цель работы: уточнение методики обработки спектров оптических характеристик композитов прозрачная матрица – наночастицы металлов с учётом оксидной плёнки на поверхности наночастиц. В качестве модельной системы исследовались композиты пентаэритрит тетранитрат – наночастицы алюминия с оболочкой из оксида алюминия. Задачи работы:
-
1. Расчёт оптических свойств наночастиц в зависимости от радиуса, массовой доли оксида и длины волны.
-
2. Расчёт спектральных зависимостей оптических свойств композитов при варьировании радиуса, массовой доли оксида и массовой доли наночастиц.
-
3. Определение возможности оценки параметров наночастиц и композита из решения обратной задачи описания спектральных зависимостей оптических свойств композита с учётом оксидной оболочки.
Решение обратной задачи: определение параметров наночастиц с учётом оксидной оболочки на основе спектральных зависимостей оптических свойств композита. Первая из поставленных задач была ре- шена на примере широкого круга систем, включающих наночастицы алюминия, покрытые оксидной плёнкой [14, 16, 17]. Вторая и третья задачи, включающие учёт многократного рассеяния излучения в образце, поставлены впервые.
1. Методика расчёта
Рассмотрим композит в виде плоскопараллельного слоя прозрачной матрицы, в которой находятся наночастицы металла с оксидной оболочкой. Способ изготовления подобного композита описан в [6, 18]. Будем считать, что наночастицы, равномерно распределённые в матрице, имеют форму шара с одним значением радиуса и толщины оксидной оболочки, которая определяется на основе массовой доли оксида. Массовая доля наночастиц считается достаточно малой, чтобы можно было пренебречь эффектами их диполь-дипольного взаимодействия [19, 20]. При равномерном распределении наночастиц типичное расстояние между ними можно оценить как удвоенное значение обратной величины кубического корня из концентрации (в см –3). Для наночастиц алюминия без оксидной оболочки с радиусом 10 нм и массовой долей 1 % в матрице с плотностью 1,77 характерное расстояние между наночастицами составит порядка r ~ 170 нм. Радиальная составляющая электрического поля вдали от наночастицы уменьшается пропорционально (2 n m 3 r / X )-2 ( m 3 - показатель преломления матрицы) [21, 22], что в наших условиях составляет менее 0,01. Это позволяет пренебречь взаимодействием наночастиц в условиях расчёта, которое наблюдается при расстояниях порядка 10 нм между ними [19, 20]. Далее будем рассматривать наночастицы алюминия. Толщина плёнки оксида L определяется при решении уравнения:
w = — m
m Al2O3
m Al2O3
!Al + m A1 2 O 3 ,
= ^3 -P Al 2 O 3 ( R 3 - ( R - L )3 ) ,
4 п mAl ( ni, Ri, L )= “3“ Pa1( R - L) , где R - радиус наночастиц, pA - плотность алюминия, pAi2O3 - плотность оксида алюминия.
Для описания процессов поглощения и рассеяния электромагнитных волн системами ядро – оболочка Аденом и Керкером была разработана соответствующая модификация теории Ми [21]. В области частот излучения видимого и ультрафиолетового диапазона магнитная восприимчивость металлов стремится к единице, поэтому нами были сделаны соответствующие упрощения. В рамках теории коэффициент эффективности поглощения (Qabs) сферическим включением рассчитывается как разность коэффициентов эффективности экстинкции (Qext) и рассеяния (Qsca) [22, 23]. Последние рассчитываются как сумма бесконечного ряда от коэффициентов разложения электрического и магнитного поля рассеянной световой волны по специальным функциям Риккати – Бесселя [17, 21]:
Qsa = f Z (21 + N C Г + bb- Г),(2)
TO
Qext =--bm Z (21 + !)• (Cl + bl),(3)
где v = 2 n m 3 R / X , m 3 - показатель преломления среды. Коэффициенты cl и bl определяются из условий на поверхностях оболочка – среда и ядро – оболочка [17, 21]. В результате выражения для коэффициентов принимают вид, приведённый в [17]:
Мощность излучения, рассеянного под углом θ без учёта поляризации (индикатриса рассеяния), равна:
+
l
11 ,2 1 +1 ( cQ ( cos e ) + b,Si ( cos e ) )
x ( e ) = 2 £ ( - 1 )'
+ 2 SH )'
l
11 TATA ( cS " ( cos e ) + b1Q ( c os e ) ) •
P ()(cos e) (1)‘ где Q1 =-----------, S1 =-sine^P1 (’(cose). Далее sin e индикатриса нормировалась на интеграл по полному телесному углу.
Выражения (1)–(6) приводят к оптическим свойствам наночастиц с радиусом R . Для показателей ослабления, рассеяния и поглощения имеем:
µ ext = π AR 2 Qext , µ sca = π AR 2 Q sca , µ abs =µ ext -µ sca ,
где введена вспомогательная переменная
Процедура расчёта оптических свойств композита, включая спектральные зависимости коэффициентов полного отражения и пропускания и коллимированного пропускания, подробно описана в работах [24–26]. Спектральные зависимости показателей преломления алюминия и оксида алюминия были взяты из [27]. По мере роста длины волны в области 260–800 нм возрастает как действительная, так и мнимая части показателя преломления алюминия, причём около 800 нм рост мнимой части замедляется около величины 8,5, а действительной – ускоряется. Данное поведение связано с существованием широкой полосы межзонного поглощения с максимумом около 850 нм. Действительная часть меньше единицы при λ < 560 нм, возрастая до 2,80 при 800 нм [27]. При увеличении длины волны от 260 до 800 нм показатель преломления оксида алюминия уменьшается от 1,834 до 1,760, мнимая часть равна нулю.
2. Результаты и обсуждение
Рассмотрим влияние массовой доли оксида на оптические свойства наночастиц. Результаты расчётов по выражениям (1)–(7) в случае двухслойной сферы в зависимости от радиуса наночастицы при значении массовой доли оксида 0 (1), 25 (2), 60 (3) и 80 % (4) приведены на рис. 1. Массовая доля наночастиц принималась равной 1 %, показатель преломления матрицы 1,54 (пентаэритрит тетранитрат), длина волны 308 нм. Увеличение массовой доли оксида приводит к уменьшению амплитуды максимума показателя рассеяния со сдвигом в область больших радиусов (рис. 1 а ). Похожая, но менее выраженная тенденция наблюдается и для показателя поглощения композита (рис. 1 б ). Так, увеличение массовой доли оксида от 0 до 80 % приводит к падению максимального показателя рассеяния в 3,02 раза, а показателя поглощения – в 2,28 раз. При уменьшении амплитуды максимума происходит его сдвиг в область больших радиусов наночастиц, поэтому возникают области радиусов, в которых увеличение массовой доли оксида не влияет на величину показателя поглощения композита. При длине волны 308 нм данные области приходятся на 32–37 и 57–65 нм. В области 32–37 нм показатель поглощения для наночастиц с массовой долей оксида 80 % даже немного больше, чем для полностью металлических наночастиц.
Массовая доля оксида оказывает также влияние и на фактор анизотропии рассеяния. При R < 85 нм рост доли оксида приводит к росту фактора анизотропии
(рис. 1 в ), причём для массовой доли оксида 80 % при радиусе наночастиц от 36 до 51 нм фактор анизотропии положителен, что типично для рассеяния на диэлектрических частицах малого радиуса. В случае рассеяния света на металлических сферах фактор анизотропии обычно отрицателен.
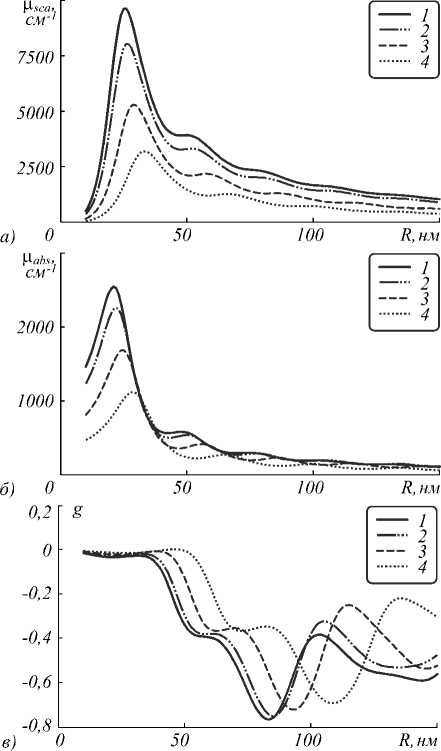
Рис. 1. Рассчитанные зависимости показателя рассеяния (а), поглощения (б) и фактора анизотропии (в) от радиуса наночастиц алюминия в матрице пентаэритрит тетранитрата при длине волны 308 нм и массовой доле оксида 0 (1), 25 (2), 60 (3) и 80 % (4)
На рис. 2 показано влияние массовой доли оксида в наночастицах с радиусом 60 нм на величины показателей рассеяния ( а ), поглощения ( б ) и фактор анизотропии рассеяния ( в ) при значениях длины волны 308 (1), 532 (2), 643 (3) и 1064 нм (4) и массовой доле наночастиц 1 %. Так как оксид обладает меньшим по модулю показателем преломления, увеличение его массовой доли и соответственный рост толщины оболочки приводят к понижению показателя рассеяния света.
Показатель поглощения также уменьшается из-за того, что оксидная плёнка не поглощает свет при всех использованных значениях длины волны. Соответственно, фактор анизотропии индикатрисы рассеяния увеличивается, давая переход от поглощающих и рассеивающих свет наночастиц к сугубо рассеивающим. Величина показателя рассеяния растёт при уменьшении длины волны (рис. 2а). Для показателя поглоще- ния эта тенденция выполняется не столь жёстко (рис. 2б). Для массовой доли оксида алюминия менее 38,5 % показатель поглощения при длине волны 643 нм выше, чем при 532 нм, а для более окисленных наночастиц – наоборот. Рис. 2б воспроизводит особенность, отмеченную на рис. 1б в случае длины волны 308 нм: показатель поглощения слабо зависит от массовой доли оксида, если она меньше 70%, после чего следует участок быстрого уменьшения пока-
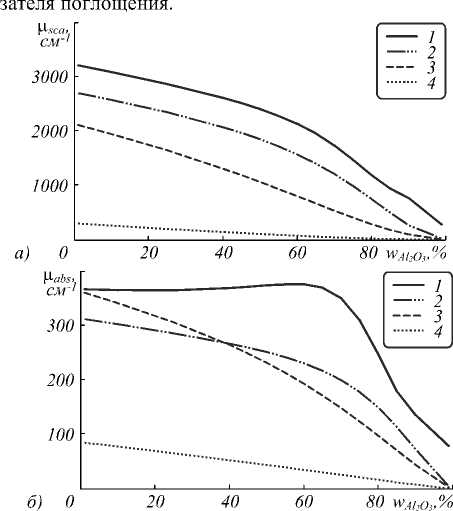
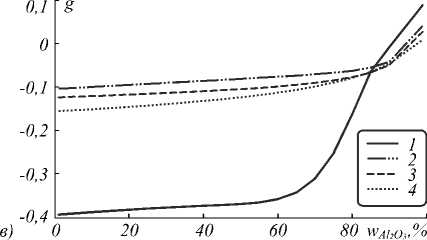
Рис. 2. Рассчитанные зависимости показателя рассеяния (а), поглощения (б) и фактора анизотропии (в) от массовой доли оксида в наночастицах алюминия с радиусом 60 нм при длине волны
308 (1), 532 (2), 643 (3) и 1064 нм (4)
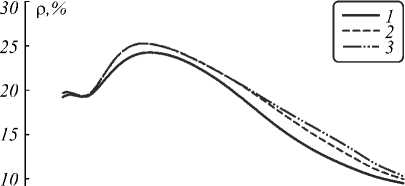
На рис. 3 показаны результаты расчётов оптических свойств композита, содержащего наночастицы алюминия с радиусом 60 нм и массовой долей 0,05 %, массовая доля оксида в наночастицах составляла 75 %, толщина слоя композита – 0,02 (1), 0,04 (2) и 0,08 см (3). Максимальное значение коэффициента полного отражения наблюдается при длине волны 398 нм, составляя 24,3 % при толщине композита 0,02 см (рис. 3а). Локальный максимум коэффициента полного пропускания сдвинут относительно него в синюю область, наблюдаясь при длине волны 354 нм с амплитудой 37,0% при той же толщине композита. Локальный минимум коэффициента полного пропус- кания находится при длине волны 443 нм, с величиной 32,2% (рис. 3б), соответствующий минимум баллистической компоненты пропускания – при 434 нм, с величиной 16,6% (рис. 3в). Хорошо видно, что минимум коэффициента пропускания коррелирует по положению с максимумом суммы показателей поглощения и рассеяния, а максимум коэффициента полного отражения – с максимумом альбедо однократного рассеяния (рис. 3г).
а) 5200 300 400 500 600 700 к нм
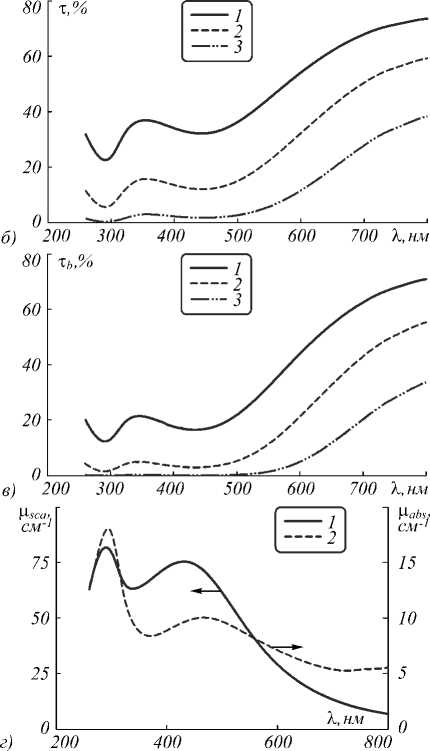
Рис. 3. Рассчитанные спектральные зависимости коэффициентов полного отражения (а) и пропускания (б) и коллимированного пропускания (в) и показателей рассеяния и поглощения для композитов толщиной 0,02 (1), 0,04 (2) и 0,08 см (3) с наночастицами алюминия радиусом 60 нм и массовой долей оксида 75%
Из представленных результатов следует, что спектральные зависимости оптических свойств компози- та, содержащего наночастицы алюминия, зависят от их радиуса, массовой доли наночастиц и массовой доли оксида при заданной величине показателя преломления матрицы. Поэтому возникает вопрос: можно ли на основе спектральных зависимостей коэффициентов отражения и пропускания оценить данные параметры одновременно? Для моделирования решения обратной задачи предполагалось, что радиус наночастиц фиксирован, наличием распределения по размерам пренебрегалось. Вначале рассчитывались спектральные зависимости коэффициентов полного отражения и пропускания и коллимированной компоненты коэффициента пропускания в области 260–800 нм с шагом 20 нм при двух значениях толщины слоя композита. Затем на полученные величины коэффициентов налагался шум с нормальным законом распределения и дисперсией 1 %. Выбранная дисперсия соответствует типичной погрешности измерения коэффициентов пропускания и отражения на современных приборах. В некоторых случаях величины коэффициентов после наложения шума становились отрицательными, что противоречит их физическому смыслу. Поэтому выполнялась проверка элементов матрицы коэффициентов пропускания и отражения с заменой отрицательных значений нулевыми. Далее выполнялся расчёт спектральных зависимостей коэффициентов полного отражения и пропускания и коллимированного пропускания света при варьировании радиуса, массовой доли оксида в наночастицах и массовой доли наночастиц с минимизацией суммы квадратов отклонений методом Нейлдера – Мида.
Пример результата решения обратной задачи приведён на рис. 4. Исходные значения радиуса наночастиц составляли 40 нм, массовой доли оксида – 40 %, массовой доли наночастиц в композите – 0,05 %.
Толщина образца составляла 0,02 и 0,04 см. Наночастицы алюминия проявляют плазмонные оптические свойства в ультрафиолетовой области спектра, что хорошо видно по максимуму коэффициента полного отражения при длине волны 328 нм с амплитудой 24,4 % и локальному минимуму коэффициента полного пропускания при длине волны 374 нм с величиной τ = 5,5 % (для толщины слоя композита 0,02 см). Коллимированная компонента коэффициента пропускания равна нулю в данной области, поэтому пропускание полностью диффузное. При движении из синей области спектра в красную прослеживается уменьшение коэффициента отражения, который при длине волны 800 нм составляет 8,5 %. Коэффициент пропускания в данном случае возрастает из-за уменьшения показателей поглощения и рассеяния. Вклад диффузной составляющей в коэффициент пропускания при толщине композита 0,02 см имеет два локальных максимума при значениях длины волны 513 (9,7 %) и 308 нм (6,5 %). При толщине композита 0,04 см максимумы смещаются до 585 (7,0%) и 306 нм (0,8 %). Локальный минимум, находящийся между двумя максимумами при толщине слоя композита 0,02 см, имеет координаты 578 нм и 6,6 %. Мак- симум ρ и локальный максимум коэффициента диффузного пропускания при 308 нм коррелирует с максимумом альбедо однократного рассеяния для данных наночастиц при 328 нм с амплитудой 0,885.
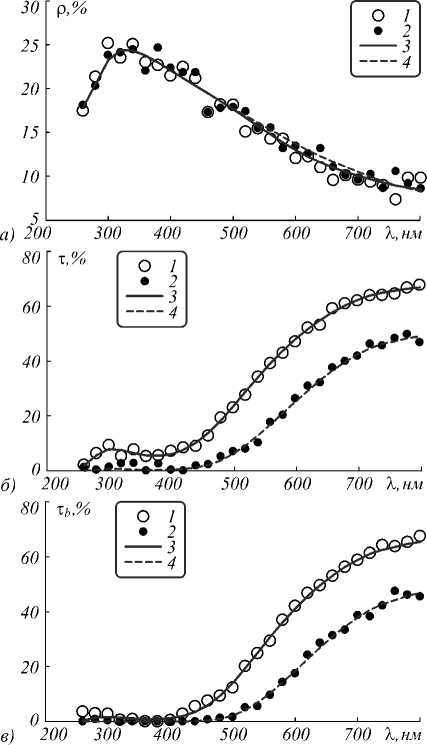
Рис. 4. Модельные (1 и 2) и полученные при решении обратной задачи (3 и 4) спектральные зависимости коэффициентов полного отражения (а) и пропускания (б) и коллимированного пропускания (в) композитов с толщиной слоя 0,02 (1 и 3) и 0,04 см (1 и 3), содержащих наночастицы алюминия с радиусом 40 нм, массовой долей 0,05 % и массовой долей оксида 40 %
В табл. 1 представлены результаты моделирования решения обратной задачи для нескольких значений радиуса наночастиц на основе спектральных зависимостей коэффициентов полного отражения и пропускания и коллимированного пропускания по той же методике. Массовая доля наночастиц во всех расчётах была одинаковой (строки 1–5), хотя в эксперименте обычно стараются подобрать оптимальную толщину образца.
Из результатов, показанных в табл. 1, следует, что наименьшая величина ошибки возникает при определении радиуса наночастицы, а массовая доля наночастиц и массовая доля оксида являются более слабыми параметрами. В частности, из пяти рассмотренных случаев максимальная относительная погрешность определения радиуса наночастицы составила 2,5 % (строка 1), а массовой доли наночастиц – 24,6 % (строка 2).
Табл. 1. Результаты решения модельной обратной задачи – определение массовой доли и радиуса наночастиц алюминия и массовой доли оксида в них на основании спектральных зависимостей оптических свойств композита
|
п/п |
Использованные параметры |
Определенные параметры |
|||||||
|
R , нм |
w , % |
w N , % |
R , нм |
δ R/R , % |
w , % |
δ w/w , % |
w N , % |
δ wN/wN , % |
|
|
1 |
40 |
40 |
0,05 |
40,00 |
2,5 |
46,17 |
15,4 |
0,0543 |
8,6 |
|
2 |
50 |
20 |
50,86 |
1,7 |
24,92 |
24,6 |
0,0520 |
4,0 |
|
|
3 |
60 |
75 |
60,49 |
0,8 |
75,81 |
1,1 |
0,0515 |
3,0 |
|
|
4 |
70 |
60 |
70,52 |
0,8 |
61,36 |
2,3 |
0,0516 |
3,2 |
|
|
5 |
80 |
30 |
79,98 |
0,03 |
30,50 |
1,7 |
0,0501 |
0,2 |
|
|
6 |
50 |
20 |
0,025 |
49,81 |
0,4 |
18,91 |
5,5 |
0,0248 |
0,8 |
|
7 |
40 |
40 |
0,025 |
40,57 |
1,4 |
45,36 |
13,4 |
0,0270 |
8,0 |
По-видимому, увеличение погрешности связано с малыми величинами коэффициентов пропускания для строк 1 и 2. Например, локальный минимум коэффициента полного пропускания для наночастиц с радиусом 40 нм (1 строка таблицы) в области 350–450 нм имеет глубину 5,5 %, тогда как для композита с радиусом наночастиц 60 нм – 32% (толщина слоя 0,02 см). В результате информативная часть спектральной зависимости приобретает повышенную относительную погрешность, что не может не сказаться на точности решения обратной задачи. Поэтому мы можем предположить, что точность определения параметров может быть повышена при подборе толщины слоя композита или массовой доли наночастиц. Для проверки был выполнен дополнительный расчёт при радиусе наночастиц 50 нм, массовой доле оксида 20% и массовой доле наночастиц 0,025 % (строка 6 табл. 1). Наблюдаемое улучшение (массовая доля оксида определена с погрешностью 5,5 %) связано с тем, что значения коэффициентов пропускания лежат ближе к оптимальной области. В частности, локальный минимум в области 440–460 нм повышается от 11,5 до 31,2%. Аналогичный результат наблюдается и для композита с R =40 нм, w =40% (строка 7 табл. 1). Таким образом, для сокращения погрешности определения параметров модели требуется подобрать толщину образцов или массовую долю наночастиц так, чтобы в области наибольшей чувствительности оптических свойств к радиусу и массовой доле оксида значения коэффициента пропускания были порядка 20–40%.
Заключение
Проведено теоретическое исследование оптических свойств композитов прозрачная матрица– наночастицы металлов одного радиуса, покрытых оксидной оболочкой, на примере композитов пентаэритрит тетранитрат – наночастицы Al (Al2O3). Оптические свойства индивидуальных наночастиц рассчитывались в рамках модификации теории Ми для концентрических структур ядро – оболочка (Адена – Керкера). Показано, что оптические свойства (показатели поглощения и рассеяния, коэффициенты полного отражения и пропускания и коллимированного пропускания) определяются радиусом наночастиц, их массовой долей и массовой долей оксида в наночастицах. Предложен способ определения данных параметров при сравнении рассчитанных спектральных зависимостей коэффициентов пропускания и отражения с экспериментом. Способ апробирован на модельных спектральных зависимостях с добавлением шумов. Показано хорошее согласие введённых и найденных параметров, особенно при оптимизации толщины образца или массовой доли наночастиц.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (Задание № 3.5363.2017/8.9) и госзадания ФАНО России (гос. задание ИУХМ ФИЦ УУХ СО РАН, проект АААА-А17-117041910150-2, руководитель Адуев Б.П).
Список литературы Моделирование спектральных характеристик композитов прозрачная матрица-наночастицы со структурой ядро-оболочка
- Братченко, И.А. Гиперспектральная визуализация патологий кожи в видимой области/И.А. Братченко, М.В. Алонова, О.О. Мякинин, А.А. Морятов, С.В. Козлов, В.П. Захаров//Компьютерная оптика. -2016. -Т. 40, № 2. -С. 240-248. - DOI: 10.18287/2412-6179-2016-40-2-240-248
- Лысенко, С.А. Метод расчёта коэффициента диффузного отражения света от глазного дна/С.А. Лысенко, М.М. Кугейко//Журнал прикладной спектроскопии. -2016. -Т. 83, № 3. -С. 419-429.
- Петрук, И.Г. Спектрофотометрический метод дифференциации меланомы кожи человека. II. Диагностические характеристики/И.Г. Петрук, A.П. Иванов, С.M. Кватернюк, В.В. Барун//Журнал прикладной спектроскопии. -2016. -Т. 83, № 2. -С. 284-292.
- Toon, G.C. HITRAN spectroscopy evaluation using solar occultation FTIR spectra/G.C. Toon, J.-F. Blavier, K. Sung, L.S. Rothman, I.E. Gordon//Journal of Quantitative Spectroscopy and Radiative Transfer. -2016. -Vol. 182. -P. 324-336. - DOI: 10.1016/j.jqsrt.2016.05.021
- Wang, C. Application of principal component analysis to classify textile fibers based on UV-Vis diffuse reflectance spectroscopy/C. Wang, Q. Chen, M. Hussain, S. Wu, J. Chen, Z. Tang//Журнал прикладной спектроскопии. -2017. -Т. 84, № 3. -С. 368-372.
- Адуев, Б.П. Определение оптических свойств светорассеивающих систем с помощью фотометрического шара/Б.П. Адуев, Д.Р. Нурмухаметов, А.А. Звеков, А.П. Никитин, Н.В. Нелюбина, Г.М. Белокуров, А.В. Каленский//Приборы и техника эксперимента. -2015. -№ 6. -С. 60-66. - DOI: 10.7868/S0032816215050018
- Guévelou, S. A simple expression for the normal spectral emittance of open-cell foams composed of optically thick and smooth struts/S. Guévelou, B. Rousseau, G. Domingues, J. Vicente//Journal of Quantitative Spectroscopy and Radiative Transfer. -2017. -Vol. 189. -P. 329-338. - DOI: 10.1016/j.jqsrt.2016.12.011
- Нелюбина, Н.В. Особенности обработки спектров окрашенных суспензий в кюветах с толстыми стенками/Н.В. Нелюбина, М.П. Пидгирный, О.Н. Булгакова, А.А. Звеков, А.В. Каленский//Компьютерная оптика. -2016. -Т. 40, № 4. -С. 508-515. - DOI: 10.18287/2412-6179-2016-40-4-508-515
- Herbin, H. New approach for the determination of aerosol refractive indices -Part I: Theoretical bases and numerical methodology/H. Herbin, O. Pujol, P. Hubert, D. Petitprez//Journal of Quantitative Spectroscopy & Radiative Transfer. -2017. -Vol. 200. -P. 311-319. - DOI: 10.1016/j.jqsrt.2017.03.005
- Hubert, P. New approach for the determination of aerosol refractive indices -Part II: Experimental set-up and application to amorphous silica particles/P. Hubert, H. Herbin, N. Visez, O. Pujol, D. Petitprez//Journal of Quantitative Spectroscopy & Radiative Transfer. -2017. -Vol. 200. -P. 320-327. - DOI: 10.1016/j.jqsrt.2017.03.037
- Адуев, Б.П. Исследование оптических свойств наночастиц алюминия в тетранитропентаэритрите с использованием фотометрического шара/Б.П. Адуев, Д.Р. Нурмухаметов, Г.М. Белокуров, А.А. Звеков, А.В. Каленский, А.П. Никитин, И.Ю. Лисков//Журнал технической физики. -2014. -Т. 84, № 9. -С. 126-131.
- Mostovshchikov, A.V. Structural and energy state of electro-explosive aluminum nanopowder/A.V. Mostovshchikov, A.P. Ilyin, M.A. Zakharova//Key Engineering Materials. -2016. -Vol. 712. -P. 215-219. - DOI: 10.4028/www.scientific.net/KEM.712.215
- Ильин, А.П. Проблемы совершенствования электровзрывной технологии получения нанодисперсных порошков/А.П. Ильин, О.Б. Назаренко//Известия высших учебных заведений. Серия: Химия и химическая технология. -2008. -Т. 51, № 7. -С. 61-64.
- Knight, M.W. Aluminum for plasmonics/M.W. Knight, N.S. King, L. Liu, H.O. Everitt, P. Nordlander, N.J. Halas//ACS Nano. -2014. -Vol. 8, Issue 1. -P. 834-840. - DOI: 10.1021/nn405495q
- Parashar, P.K. Plasmonic silicon solar cell comprised of aluminum nanoparticles: Effect of nanoparticles' self-limiting native oxide shell on optical and electrical properties/P.K. Parashar, R.P. Sharma, V.K. Komarala//Journal of Applied Physics. -2016. -Vol. 120. -143104. - DOI: 10.1063/1.4964869
- Temple, T.L. Optical properties of gold and aluminium nanoparticles for silicon solar cell applications/T.L. Temple, D.M. Bagnall//Journal of Applied Physics. -2011. -Vol. 109. -084343. - DOI: 10.1063/1.3574657
- Адуев, Б.П. Влияние массовой доли металлического алюминия в наночастицах на порог взрывного разложения и эффективность поглощения света в компаунде на основе тэна/Б.П. Адуев, Д.Р. Нурмухаметов, А.А. Звеков, Н.В. Нелюбина//Физика горения и взрыва. -2014. -Т. 50, № 5. -C. 87-91.
- Адуев, Б.П. Исследование вкладов рассеяния и поглощения света включениями наночастиц алюминия в тэне/Б.П. Адуев, Д.Р. Нурмухаметов, Г.М. Белокуров, Р.И. Фурега//Физика горения и взрыва. -2015. -Т. 51, № 3. -С. 70-75. - DOI: 10.15372/FGV20150310
- Наноплазмоника/В.В. Климов. -М: Физматлит, 2009. -480 с. -ISBN: 978-5-9221-1030-3.
- Rasskazov, I.L. Surface plasmon polaritons in curved chains of metal nanoparticles/I.L. Rasskazov, S.V. Karpov, V.A. Markel//Physical Review B. -2014. -Vol. 90, Issue 7. -075405. - DOI: 10.1103/PhysRevB.90.075405
- Aden, A.L. Scattering of electromagnetic waves from two concentric spheres/A.L. Aden, M. Kerker//Journal of Applied Physics. -1951. -Vol. 22, Issue 10. -P. 1242-1246. - DOI: 10.1063/1.1699834
- Рассеяние света в мутной среде/К.С. Шифрин. -М., Л.: Гос. изд-во технико-теоретической лит., 1951. -288 c.
- Кригер, В.Г. Влияние эффективности поглощения лазерного излучения на температуру разогрева включения в прозрачных средах/В.Г. Кригер, А.В. Каленский, А.А. Звеков, И.Ю. Зыков, Б.П. Адуев//Физика горения и взрыва. -2012. -Т. 48, № 6. -С. 54-58.
- Звеков, А.А. Моделирование распределения интенсивности в прозрачной среде с френелевскими границами, содержащей наночастицы алюминия/А.А. Звеков, А.В. Каленский, А.П. Никитин, Б.П. Адуев//Компьютерная оптика. -2014. -Т. 38, № 4. -С. 749-756.
- Звеков, А.А. Расчёт оптических свойств композитов пентаэритрит тетранитрат -наночастицы кобальта/А.А. Звеков, А.В. Каленский, Б.П. Адуев, М.В. Ананьева//Журнал прикладной спектроскопии. -2015. -Т. 82, № 2. -С. 219-226.
- Каленский, А.В. Оптические свойства композитов на основе прозрачной матрицы и наночастиц меди/А.В. Каленский, А.А. Звеков, А.П. Никитин, Н.В. Газенаур//Известия высших учебных заведений. Физика. -2016. -Т. 59, № 2. -С. 87-94.


