Моделирование СШП-импульса на основе производных Рэлея и генетического алгоритма

Современная технология сверхширокополосной (СШП) радиосвязи является перспективным направлением развития высокоскоростной передачи данных на короткие расстояния, обеспечивающей низкое энергопотребление, упрощение построения аппаратуры и снижение стоимости затрат, а также высокую спектральную эффективность. Реализация данных преимуществ подразумевает разработку особых методов формирования, обработки, передачи и приема сигналов, что подтверждается значительным количеством исследований и публикаций, представленных за последние годы.

Согласно определению Федерального агентства по связи США (Federal Communications Commission, FCC), для СШП-систем выделен диапазон частот 3,1 … 10,6 ГГц, что подразумевает совместную одновременную работу с другими радиоустройствами. В связи с этим определены нормы на уровень эффективной излучаемой мощности для СШП-устройств – так называемая спектральная маска FCC.

В рамках данных ограничений возникает интересная задача формирования импульса, спектральная плотность мощности (СПМ) которого соответствовала бы маске FCC. Большинство работ, посвященных данной тематике, основано на применении гауссова импульса и его производных, взятых в различных комбинациях, поскольку их легко описывать и генерировать с помощью аналоговых схем. В частности, в [1] оптимальный импульс получен как сумма первой, четвертой и пятой производных, оптимизированных «методом роя частиц» (particle swarm optimization – PSO). Линейная комбинация первых пятнадцати производных, подобранных по «методу проб и ошибок» (trial and error), представлена в [2]. Пятая производная Гаусса с коэффициентом формы σ = 41 пс удовлетворяет маске FCC согласно [3], но неприемлема для создания недорогих маломощных устройств.

Постановка задачи

Согласно теореме Парсеваля эффективность излучения импульса обеспечивается равенством нулю энергии сигнала s ( t ) и его преобразования Фурье S ( f ) при f = 0:

Ш'Й = «(/)|М=о.

В данной работе поставлена задача проектирования СШП-импульса, соответствующего требованиям спектральной маски FCC, представленной на рис. 1, на основе применения производных Рэлея, поскольку они удовлетворяют выражению (1) и не имеют постоянной составляющей [4].

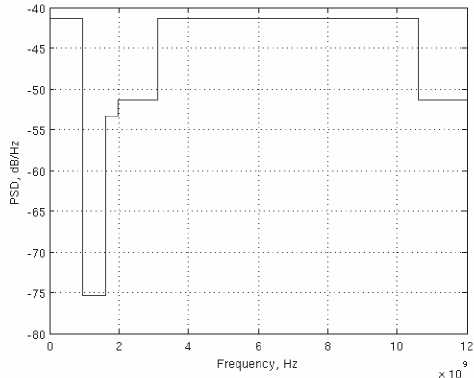
Рис. 1. Спектральная маска FCC

Применение производных объясняется тем, что если на вход антенны подать некоторый импульс, то выходной сигнал ввиду особенностей антенны будет представлять собой производную от входного воздействия. С целью максимизации использования выделенного диапазона частот выбор весовых коэффициентов и коэффициентов формы предлагается осуществить посредством генетического алгоритма (ГА), представляющего собой довольно простой и прозрачный в реализации метод оптимизации и поиска минимума функции, основанный на концепциях естественного отбора и генетики.

Решение

Временная форма, соответствующая распределению Рэлея, может быть записана следующим образом:

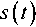
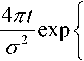
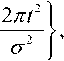
где σ – коэффициент формы импульса. Тогда n -ная производная Рэлея задается выражением:

_sW^ ₌ _^_s^^_^_sU-2^_ty  (3)

СУ                 СУ

Пребразование Фурье для нее (рассматриваем амплитудный спектр):

l^ (/)| = ^Р""' ехр | ^ f^" I. (4)

Дифференцируя (4) и приравнивая к нулю, получаем максимальную частоту спектра

^Ч"’^ о-(2я-/)"/ ._.х

—— ---' = г (2л-(/7 +1)-2(^0-/)")х df 14 л:(5)

I 2 J

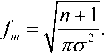
Тогда, учитывая, что максимальное значение спектра на данной частоте равно:

^"’ЧЛ,)!

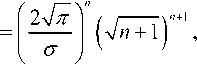
получаем выражение для нормированной СПМ:

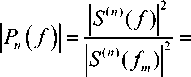
= (СТ/)2и+2

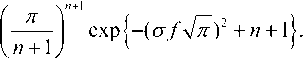
Нормирование производится относительно пикового значения, разрешенного маской FCC и равного -41,3 дБм/МГц. Поскольку численные расчеты по моделированию импульсов проводились в среде MATLAB, то для проверки адекватности результатов СПМ была также рассчитана как преобразование Фурье от автокорреляционной функции сигнала.

Временные зависимости первых пяти производных Рэлея представлены на рис. 2, а их нормированные СПМ – на рис. 3.

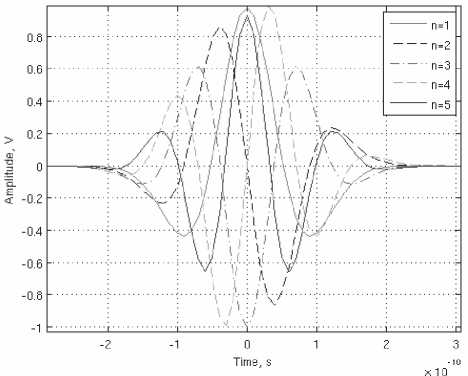
Рис. 2. Временная форма производных Рэлея, и = 1 ...5

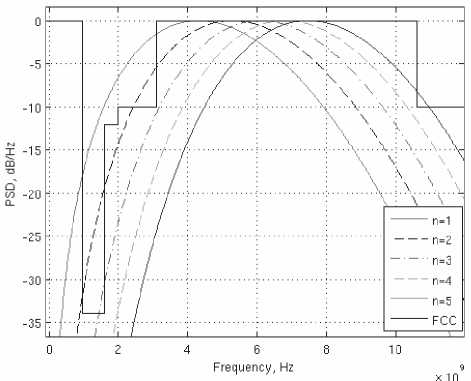
Рис. 3. Нормированные СПМ производных Рэлея, /7-1 ... 5

Возможность регулирования СПМ импульса для соответствия маске FCC определяется выбором определенного значения коэффициента формы σ. На основе экспериментальных данных установлено, что первая, вторая и третья производные не удовлетворяют маске FCC при любом значении σ, и поскольку для синтеза предпочтительнее использовать производные низших порядков ввиду простоты реализации, то выбран импульс порядка n = 4, для которого

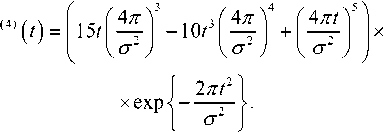
Динамика изменения СПМ четвертой производной Рэлея в зависимости от значения коэффициента формы показана на рис. 4. Уменьшение значения σ во временной области приводит к смещению СПМ в область более высоких частот и расширению полосы.

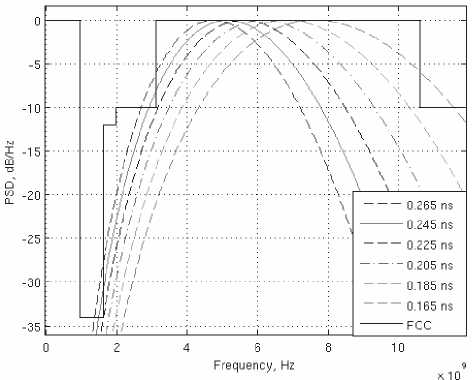
Рис. 4. Нормированные СПМ четвертой производной Рэлея с различными значениями σ

Очевидно, что для увеличения спектральной эффективности оптимальный импульс должен быть представлен в виде:

N

^(О^Е^--^(^^ (10)

где w_i – весовой коэффициент. В данном случае используется сумма производных одного порядка, но с разными значениями коэффициентов формы.

Пусть N = 2, тогда будем искать решение на основе ГА [5] в виде вектора [ w ₁, w ₂, σ ₁, σ ₂], представляющего собой набор генов – генотип.

Ниже представлены основные этапы ГА.

• 1.    Первоначально случайным образом создается некоторая комбинация, к которой применяются генетические операторы (скрещивание и мутация).

• 2.    Далее полученное множество решений оценивается при помощи целевой функции, и производится селекция лучших вариантов.

• 3.    Если оптимальное решение найдено, то цикл завершается.

• 4.    В противном случае к полученному генотипу снова применяются генетические операторы.

Зададим целевую минимизируемую функцию:

Fa = ^\P^U'VP₀^df..   (11)

где P _opt – СПМ оптимального импульса в диапазоне частот 3,1 … 10,6 ГГц; P _FCC – СПМ маски FCC. Модернизируем последовательность действий следующим образом.

• 1.    При помощи ГА рассчитаем значение σ ₁ для первого импульса таким образом, чтобы вписать левый фронт в маску FCC.

• 2.    Аналогично для второго импульса рассчитаем значение коэффициента формы σ ₂ так, чтобы зафиксировать правый фронт.

• 3.    Суммируем полученные импульсы с коэффициентами w ₁, w ₂, рассчитанными также по ГА. Конечный результат получаем в виде вектора [0,226 0,180 0,982 0,684].

СПМ смоделированного импульса, представленная на рис. 5, соответствует маске FCC, но использование спектра не эффективно. Назовем этот импульс субоптимальным РИ1.

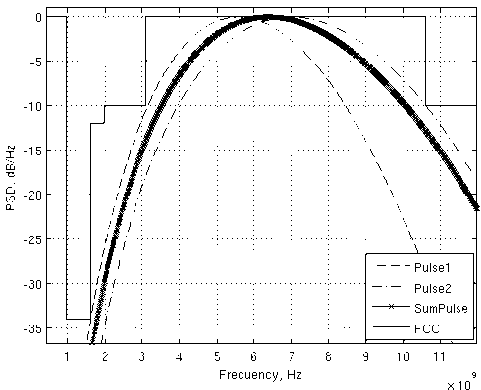
Рис. 5. Нормированные СПМ: Pulse1 ( σ ₁ = 0,226 нс), Pulse2 ( σ ₂ = 0,180 нс), SumPulse (суммарный импульс РИ1)

Тогда рассчитаем первоначальные значения коэффициентов σ ₁ и σ ₂ таким образом, чтобы одиночные импульсы несколько выходили за границы маски, и зададим дополнительную целевую функцию F ₂, максимизирующую эффективность использования спектра, в виде

p

F ₌ ^pt_

P

1 FCC

Рассчитанные значения параметров представлены в таблице 1, а суммарный оптимальный импульс РИ2 и его СПМ – на рис. 6-7:

^pt(O ^{= w}i •s₁⁽⁴⁾(Xcr_|) + M’₂ -5*⁴⁾(/,сг₂). (13)

Таблица 1. Расчетные значения параметров импульсов РИ1; РИ2 и ГИ

	РИ1	РИ2	ГИ
<71	0,226 нс	0, 245 нс	0,0915 нс
<72	0,180 нс	0,165 нс	0,0435 нс
W]	0,982	1,999	-1,07
vv2	0,684	0,416	1,081

Можно видеть, что данный комбинационный импульс отлично вписывается в маску FCC и при этом обладает высокой спектральной эффективностью .

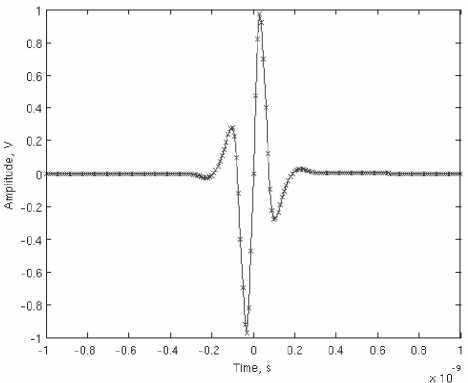
Рис. 6. Временная форма оптимального импульса РИ2

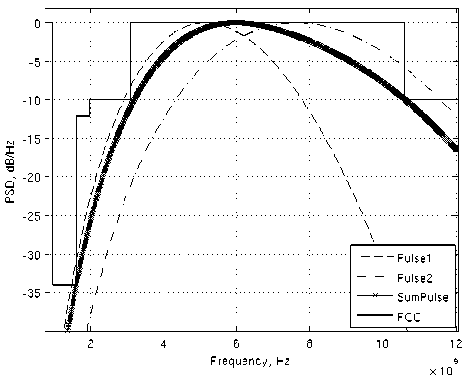
Рис. 7. Нормированные СПМ: Pulse1 ( σ ₁ = 0,245 нс), Pulse2 ( σ ₂ = 0,165 нс), SumPulse (суммарный импульс РИ2)

Применим данный алгоритм расчета к третьей производной гауссова импульса:

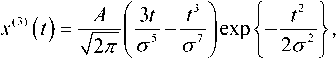
где A – амплитуда импульса, А = w_i .

Аналогичным образом рассмотрим оптимизируемый импульс ГИ1 как сумму двух компонентов. Результаты расчета генотипа и соответствующие им графики представлены в таблице 1 и на рис. 8-9. При этом наблюдается существенное совпадение формы РИ2 и ГИ как во временной, так и в частотной областях. В таблице 2 приведено сравнение полученных импульсов с представленными в литературе по целевой функции F ₂ (12).

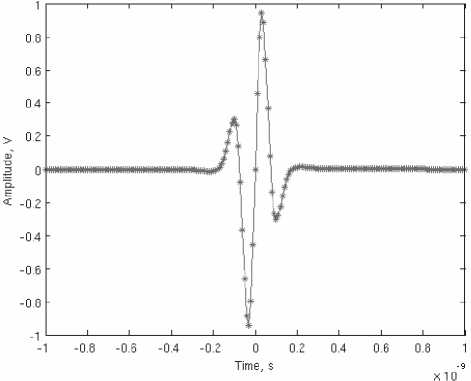
Рис. 8. Временная форма оптимального импульса ГИ1

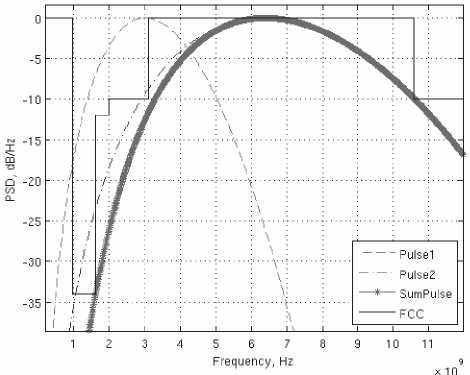
Рис. 9. Нормированные СПМ: Pulse1 ( σ ₁ = 0,0915 нс), Pulse2 ( σ ₂ = 0,0435 нс), SumPulse (суммарный импульс ГИ1)

Таблица 2. Результаты сравнения импульсов

Название импульса	%
Маска FCC	100
РИ2	93,6
ГИ1	92,09
5 производная Гаусса [3]	90,11
ГИ2 [6]	35,67
ГИЗ [7]	31,81
ГИ4 [7]	32,40

В рассматриваемом случае ГИ2 – импульс, представляющий собой комбинацию четырех субимпульсов, каждый из которых оптимален в своем диапазоне и составлен не менее чем из восьми гауссовых производных порядков n = 1 … 15, выбранных по «методу проб и ошибок» [6]. ГИ3 – линейная комбинация первых 15 производных Гаусса с одинаковыми весовыми коэффициентами σ = 0,35 нс [7], ГИ4 – с различными [7]. Спроектированный импульс РИ2 незначительно превосходит по СПМ пятую производную Гаусса и ГИ1. А по сравнению с ГИ2 … ГИ4 выигрыш в среднем составляет 60%.

Выводы

В работе представлена методика моделирования СШП-импульса, удовлетворяющего спектральной маске FCC. Предложенный импульс представляет собой линейную комбинацию двух четвертых производных Рэлея. Результаты моделирования показывают высокую спектральную эффективность и отличное соответствие маске FCC. Малое число используемых производных и их низкий порядок позволяют обеспечить простую реализацию на основе КМОП-технологии.

Исследование поддержано грантом Европейского Союза «Erasmus Mundus Action 2». Авторы выражают благодарность профессору P. Rocca за полезное обсуждение.