Моделирование статистических характеристик электромагнитного поля апертурной случайной антенны
Автор: Красильникова Екатерина Павловна, Маслов Олег Николаевич, Раков Александр Сергеевич
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Электромагнитная совместимость и безопасность оборудования
Статья в выпуске: 2 т.12, 2014 года.
Бесплатный доступ
В статье представлены результаты определения уровней электрической Е-составляющей и магнитной Н-составляющей электромагнитного поля (ЭМП), создаваемого апертурной случайной антенной (АСА). Представлены результаты статистического имитационного моделирования (СИМ) характеристик ЭМП АСА в полосе частот 10 кГц... 10 ГГц.
Апертурная случайная антенна (аса), амплитудные и фазовые ошибки, метод статистического имитационного моделирования, характеристики электромагнитного поля
Короткий адрес: https://sciup.org/140191690
IDR: 140191690 | УДК: 621.396.677;
Текст научной статьи Моделирование статистических характеристик электромагнитного поля апертурной случайной антенны
Направленные свойства апертурной случайной антенны (АСА) [1] в виде прямоугольного отверстия в проводящем экране исследованы в [2-4] методом статистического имитационного моделирования (СИМ) на частотах, ограниченных снизу условиями применимости разработанной математической модели. В настоящей статье представлена математическая модель, свободная от ограничений [2-4], и приведены итоги тести- рования СИМ-модели и данные СИМ структуры ЭМП на частотах 10 кГц … 10 ГГц. Разработка СИМ-модели как один из важных этапов проектирования системы защиты конфиденциальной информации коммерческого назначения от утечки через АСА [5] является актуальным практическим приложением статистической теории антенн (СТА) [1; 6-8].
Математическая модель АСА для проведения СИМ
Геометрию задачи по аналогии с [2-4] иллюстрирует рис. 1: прямоугольная АСА с размерами расположена на поверхности SA , совпадающей с плоскостью X0Y системы глобальных декартовых координат; расстояние от SA до плоскости SМ , в которой определяется структура ЭМП, равно RA ; расстояние от элемента АСА, расположенного в точке МА на поверхности SA , до точки наблюдения МS на плоскости SМ есть rA .
Источник ЭМП, расположенный слева от SA в точке М0 с координатами Х0 ; Y0 ; Z0 , создает в раскрыве АСА сложное по структуре возбуждающее
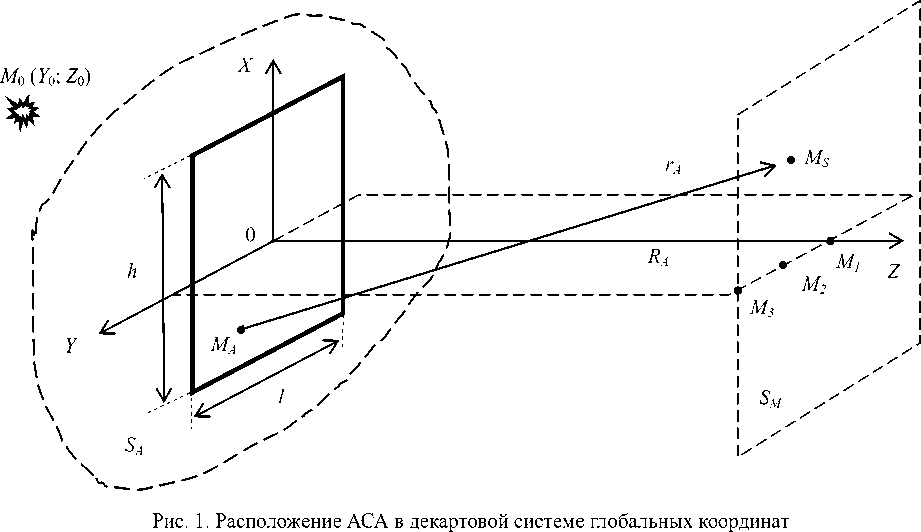
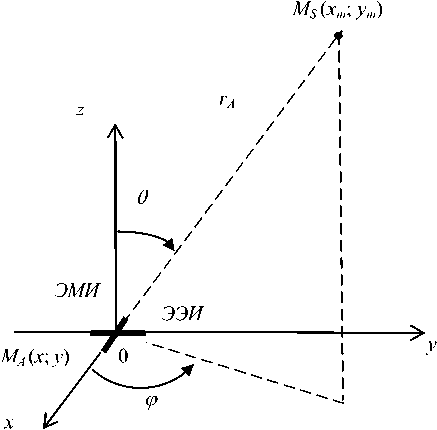
Рис. 2. Расположение ЭЭИ и ЭМИ в точке MA ( x ; у ) на плоскости SA в системе совмещенных локальных декартовых и сферических координат
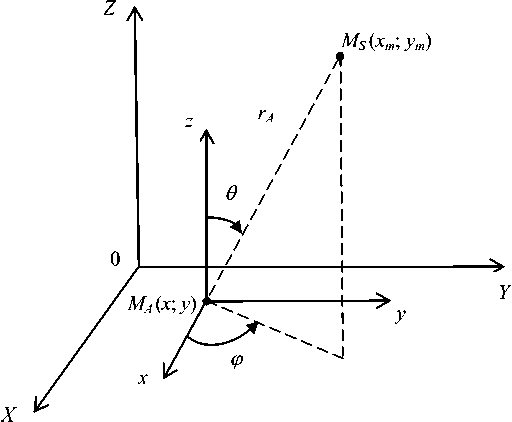
Рис. 3. Расположение ЭГ в точке MA ( x ; у ) на плоскости SA в совмещенных системах декартовых глобальных координат и локальных и сферических
локальных координат поле Ео с круговой частотой оу,, соответствующей к -ой гармонике его частотного спектра.
Элемент АСА, расположенный в точке МА, представляет собой излучающий элемент Гюйгенса (ЭГ) с площадью dS = dx-dy, в котором виртуальный электрический ток гэ = Ед dx! Zc и направлен вдоль оси у; магнитный ток iM = — EAdy и направлен вдоль оси x; где Ел - амплитуда напряженности поля, возбуждающего АСА; Zc - волновое сопротивление окружающей среды. Такой излучатель можно представить в виде двух взаимно перпендикулярных элементарных излучателей: электрического (ЭЭИ) длиной /э с током 1Э и магнитного (ЭМИ) длиной 1М с током iM , совмещенные центры которых расположены в центре локальной системы декартовых и сферических координат, как это показано на рис. 2.
При совместном возбуждении ЭЭИ и ЭМИ в гармоническом режиме комплексные амплитуды квадратурных составляющих (КС) векторов электрической Е -составляющей и магнитной Н -составляющей ЭМП согласно [9] будут равны:
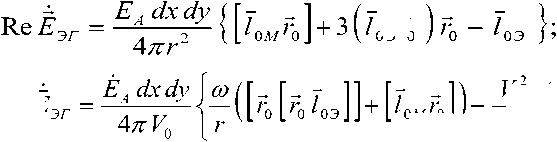
оз'о
ОМ ■ о
ImE
„ Ел d.xdy Нт Т -
Re//)z — 2 |[/оэго] ^Уомго
4тг г
о
й)г3
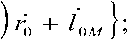
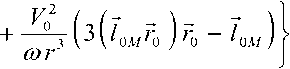
Поскольку единичные векторы, соответствующие принятому расположению ЭГ в глобальной и локальной системах декартовых координат [2-4], одинаковы: /оэ = j0; \ = х0, в совмещенных локальных декартовых и сферических координа тах (см. рис. 2 и рис. 3) единичный вектор r0 = х0 cos^psin 0 + Уо sin^psin в + z0 cos О .
Выполним векторные преобразования в (1)-(4), учтем, что (О = 2 л Ко / X , и запишем в окончательном виде для КС всех ортогональных составляющих (ОС) комплексных амплитуд рассматриваемых векторов :
Re£Y
Im Ёх
Re£y. =
Im£y =
Re£z =
Im£z =
Re//V
I mH Y
ReHy
1тЯу
ReHz
ImHz :
Ё .dxdy . •
—— sin
ф
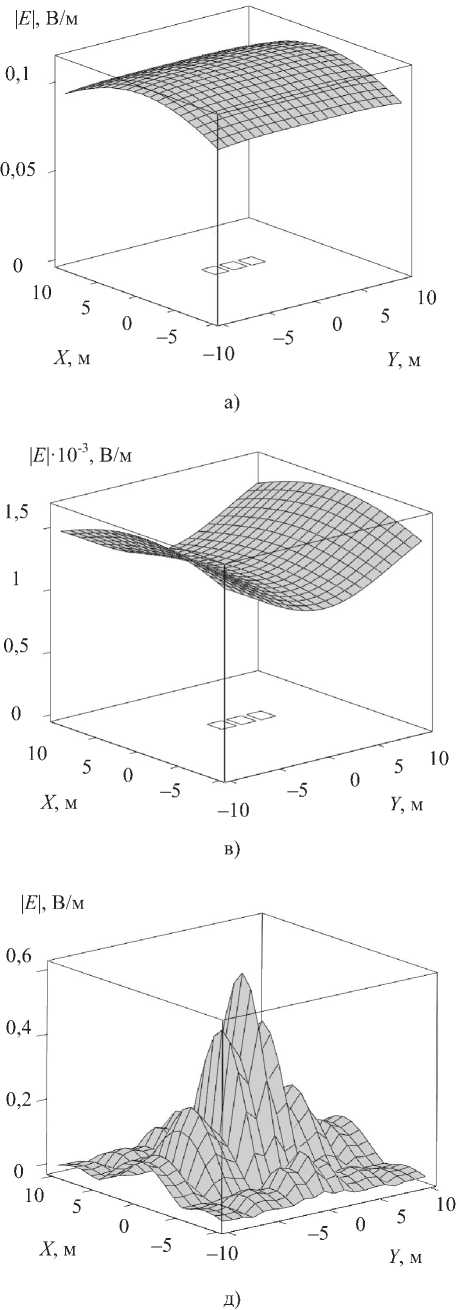
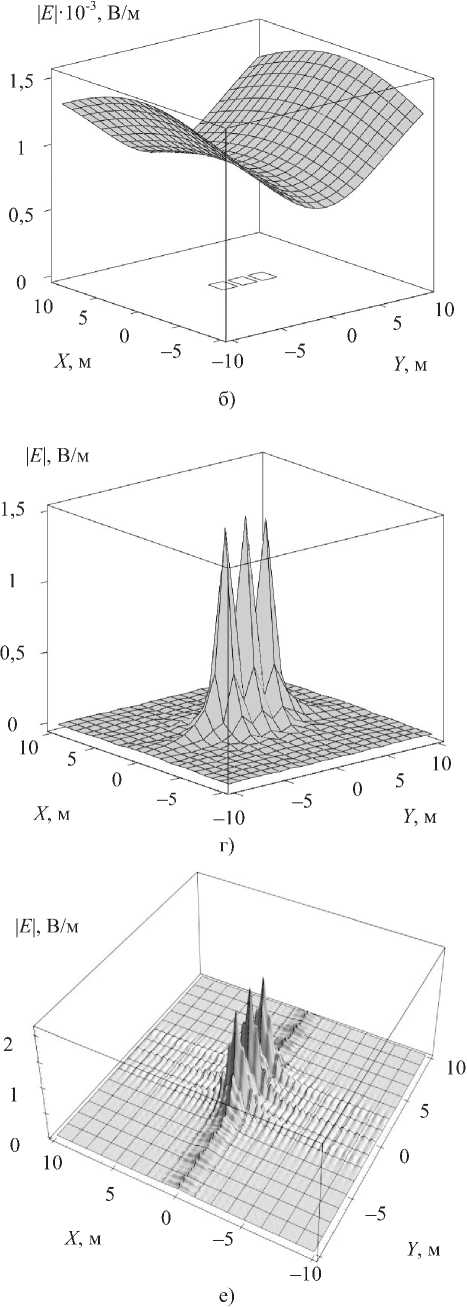
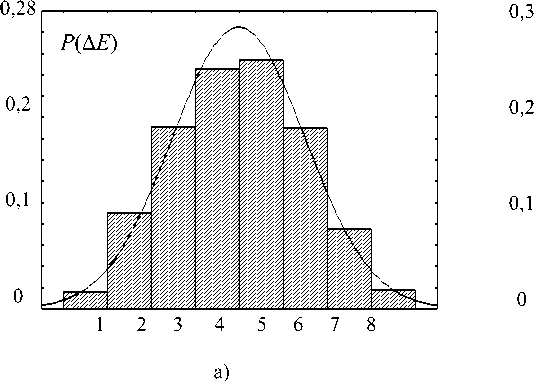
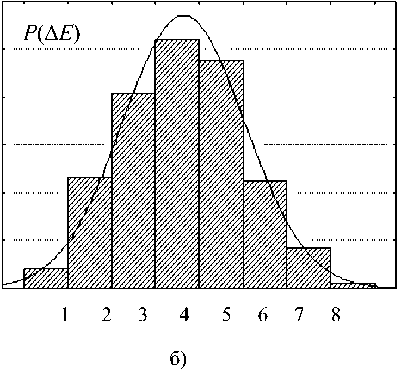
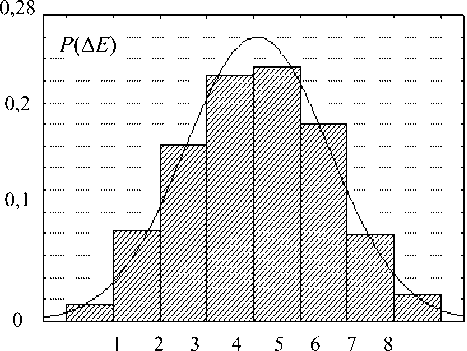
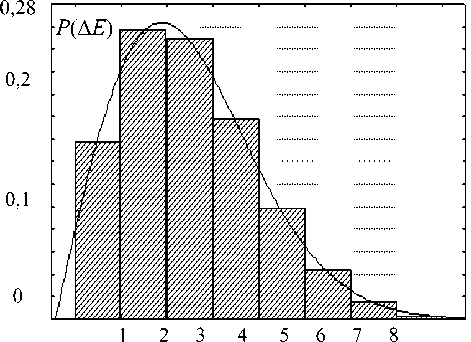
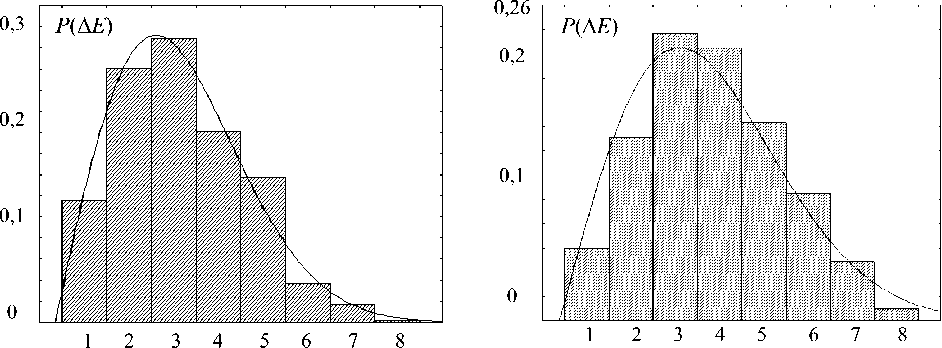
cos 9 E 4 dx dy ЁА dxdy 2 71 Ё ■ • 1 ЗА Sin ф COS69 Sin 9---;—7 \Ar АягЁ (3sin2 ^?sin29 -1 - cos 9^ ЁА dxdy 2 Ё A dx dy Ёд dx dy 2 ЁА dxdy 2лт2 (cos2ф sin29 + cos29 + cos9) — -I Ar (3sin° tp sin29 -1) sin q> sin 9 (3 cos 9 +1) 1____ 4л-2 г3 2яЁ 1 I sin ^> sin Я (cos Я + 1) — - Ё4dxdy . . —-----sin ф sin 9cos 9 3л 4л-2Ё ЁА ^Х(^ (3 cos2ф sin29 - cos 9 - 1) ЁА dx dy 2ZC ЁА dxdy 2Z„ 2 71 Ё (sin2ф sin29 + cos29 + cos9) — + Ar (3cos2ф sin29 -1) EAdxdy . . 2 A —------Sin ф COS^7 sin 9 Ё А dxdy 2Zr. 4л"2г3 3 2яЁ . • ч J 1 ЗА sin^cos^sin' 9--1--^-^ . A i 4л" r~ Ед dxdy —--- cos ф cos 9 (1 + 3 sin 9) Ё А dx dy 2ZC Ё4 dxdy 2Zr 1 cos^cos61(l + sin^) — cos ф sin 9 cos 9 3/1 4л-2Ё 2яЁ (И) (14) (is: Далее отметим, во-первых, что поскольку для n-ой гармоники (О п ='2tiVq ! Хп, то в (1)(16) для КИ-сигнала с заданным энергетическим спектром фигурируют вместо (О и X параме тры о и Я„. Во-вторых, что при выводе (1)(16) учтено предполагаемое равенство значений волнового сопротивления среды ZC в раскрыве АСА и внешнем пространстве. Рис. 4. Пространственная ориентация ОС вектора Ет В-третьих, что расстояние г — гд здесь может как соответствовать, так и не соответствовать условию k rA >> 1 для дальней (волновой) зоны Фраунгофера, что являлось ограничением в [2-4], где к = Ти IX - волновое число, однако размеры каждого элементарного излучателя в составе АСА (моделируемого в виде ЭГ) Ух ~ dx и Ny ~ dy должны отвечать условиям к^х « 1; кУу « 1, и это необходимо будет учитывать при разбиении АСА на элементы с учетом текущих значений rA и X. В-четвертых, что (5)-(16) для ЭГ получены в системе совмещенных локальных декартовых и сферических координат, тогда как для вычисления уровней Е- и Н-составля ющих ЭМП от АСА путем интегрирования полей, создаваемых всеми элементами ее раскрыва, целесообразно перейти в глобальную систему декартовых координат. Ориентацию ОС вектора Ет в точке наблюдения MS (xm; ym) для излучателя, размещенного в центре координат, иллюстрирует рис. 4. Соотношения (5)-(16) представляют собой математическую модель ЭМП, которое создает ЭГ, расположенный в точке МА с координатами x; у, в точке наблюдения MS с координатами xm; ym (см. рис. 3). Можно считать, что их уровни являются дифференциалами КС и ОС для ЭМП, создаваемого АСА в целом: d Ё^ = х0 (ReЁх + j 1тЁА.); d Ёу8 = у0 (ReЁу + j Im Е}); dЁzs = z0 (Re^ + j ImEz); d H xs = x0 (ReHx + j!mHx); dHYS = y0 (ReHY + jImHY); d Hzs = z0 (ReHz + jImHz), где нижние индексы «5» соответствуют ОС и КС для АСА в целом. Алгоритм вычисления уровней ОС и КС для АСА в целом реализуется по следующей схеме: 1) задать точку наблюдения MS с фиксированными координатами xm; ym ; zm; 2) задать на раскрыве АСА точку МА с текущими координатами x; у ; z; 3) определить согласно рис. 5-7 текущие значения sin ф ; cos ф; cos О и rA; 4) вычислить согласно (5)-(16) уровни КС и ОС для ЭМП, создаваемого в точке MS элементом раскрыва АСА с текущими координатами x; у ; z; 5) повторить действия согласно п. 2-4 для всех точек MА – то есть проинтегрировать путем численного суммирования уровни ОС и КС, создаваемые в точке MS всеми элементами раскрыва АСА; 6) сгруппировать результаты интегрирования по КС и ОС в соответствии с обозначениями (5)-(17). Результатом интегрирования по площади прямоугольной апертуры на рис. 1 (для многоэлементной АСА [2-4] – по площади всех апертур, входящих в состав АСА), являются действительные и мнимые части (то есть КС) составляющих напряженности поля всех ОС: Exs ; Eys ; Ezs ; H^ ;HYS ; Hzs . Амплитудные значения Е- и Н-составляющих ЭМП АСА определяются по следующим формулам: Eg Результаты СИМ На рис. 5а-е представлены результаты тестового расчета распределений модуля вектора I E | в пределах прямоугольной плоскости Sс центром в точке R4 = 30 м и размерами 20×20 м2, найденные согласно (11) при отсутствии ошибок для частот, соответственно, 1 кГц; 700 кГц; 1 МГц; 500 МГц; 1 ГГц и 10 ГГц. Приведенные графики иллюстрирует выпуклую (см. рис. 5а) и вогнутую седлообразную (см. рис. 5б-в) структуру ЭМП на частотах 10 кГц … 1 МГц; а также структуру с тремя основными и множеством побочных максимумов (см. рис. 5г-е) на частотах 500 МГц … 10 ГГц. Данные рис. 5 хорошо соответствуют физическим соображениям о принципах работы АСА и позволяют признать результаты тестирования разработанной модели удовлетворительными. Методика СИМ при кластерном моделировании пространственных корреляционных связей между ошибками рассмотрена в [2-4]. На рис. 6а-е представлены гистограммы случайных уровней IE | для центральной точки поверхности ^ ду при равномерных распределениях амплитудных a [–0,2; 0,2] и фазовых Ф [– ^ФмАХ^Ф ] ошибок. Значения были найдены с учетом физического моделирования условий возбуждения АСА [10] – они зависят от частоты, поскольку случайные перемещения источника возбуждения АСА (см. рис. 1) необходимо соотносить с длиной волны излучаемого сигнала. В результате на частоте 10 кГц, где фазовыми ошибками можно пренебречь, ^Фмлх = 1°; на частотах 700 кГц и 1 МГц было принято ^ФМАХ = 3°; на частотах 500 МГц и выше ^ФМАХ = 180°. Аналогичным образом число корреляционных кластеров в пределах одной апертуры на частотах 1 МГц и ниже принималось равным Ккл = 1, тогда как на частотах 500 МГц и выше N = 4. Физически это означает, что на частотах 1 МГц и ниже учиты- вались в основном амплитудные ошибки, постоянные в пределах одной апертуры (которая по площади равна одному кластеру), но изменяющиеся от апертуры к апертуре. На частотах 500 МГц и выше амплитудные и фазовые ошибки не изменялись внутри каждого из четырех кластерных «квадрантов» в пределах одной апертуры при равновероятных значениях фазовых ошибок, поскольку Ф [–180°; 180°]. На оси абсцисс рис. 6 для удобства обозначений указаны номера восьми интервалов, соответствующих динамическому диапазону с границами EMIN ; EMAX, значения которых для разных частот приведены в таблице 1. Сплошные кривые на рис. 6 соответствуют типовым вероятностным функциям, которые наилучшим образом аппроксимируют гистограммы Р(ЕЕ) в соответствии с методикой стандартной программы Easy Fit для уровня значимости 0,1 по критериям Колмогорова-Смирнова и Пирсона: на частотах 10 кГц … 1 МГц наилучшей аппроксимирующей функцией является нормальный закон, на частотах 500 МГц … 10 ГГц – закон Релея. Это объясняется тем, что в данном случае , во-первых, Eys >> ^zs^ ^xs = 0 и в условиях применимости центральной предельной теоремы теории вероятностей (особенно при увеличении числа кластеров Нкл ) распределения КС у Е приближаются к нормальному закону [2-4], что ведет к распределению модуля IЕ | по закону Райса (обобщенному распределению Релея). Во-вторых, на частотах 10 кГц … 1 МГц регулярная составляющая ЭМП существенно преобладает над нерегулярной ввиду малого влияния фазовых ошибок (так как здесь МмАХ< 3°), что делает закон Райса близким к нормальному закону, тогда как на частотах 500 МГц … 10 ГГц «вес» нерегулярной составляющей резко возрастает ввиду ^ф = 180° и закон Райса приближается к закону Релея [9]. Рис. 5. Распределения модуля напряженности поля АСА при отсутствии ошибок а) на частоте 10 кГц; б) на частоте 700 кГц; в) на частоте 1 МГц; г) на частоте 500 МГц; д) на частоте 1 ГГц; е) на частоте 10 ГГц е) Рис. 6. Гистограммы случайных значений модуля Е напряженности поля АСА а) на частоте 10 кГц; б) на частоте 700 кГц; в) на частоте 1 МГц при Мкл= 1; г) на частоте 500 МГц; д) на частоте 1 ГГц; е) на частоте 10 ГГц при Мкл = 4 Таблица 1. Динамический диапазон случайных значений модуля Е, В/м Частота 10 кГц 700 кГц 1 МГц 500 МГц 1 ГГц 10 ГГц Emin', В/м 9.2-10 2 7,5-10^ I03 1.7-10 2 1.2-10 2 2,7-10 2 Emax ; В/м 0,134 1,2-103 1,45-1О3 0,344 0,656 1,929 Заключение В статье для трехэлементной АСА прямоугольной конфигурации методом СИМ определены статистические характеристики ЭМП в заданной области окружающего пространства (без ограничений, принятых для математической модели [2-4]). Приведены данные тестирования и результаты применения разработанной СИМ-модели на частотах 10 кГц … 10 ГГц в интересах проектирования систем защиты коммерческой КИ от утечки через АСА [1; 5], что является одним из актуальных приложений СТА. Продолжение исследований в данном направлении связано с моделированием неопределенностей, присущих СИМ структуры и параметров ЭМП, создаваемого реальными АСА (проблема определения случайных ошибок [10]) методами и средствами теории систем и системного анализа. Кроме того, представляет интерес изучение особенностей работы АСА в режиме излучения и приема несинусоидальных (шумовых, шумоподобных, импульсных, радиоимпульсных и т.п.) сигналов [1], переносящих КИ.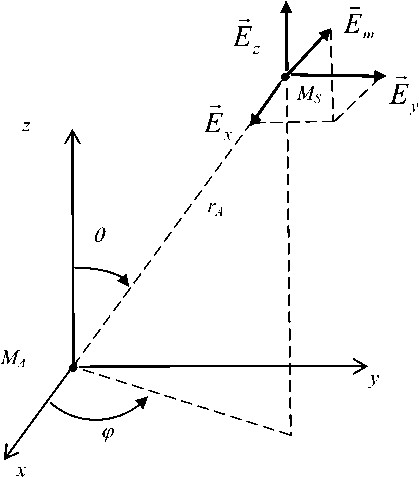
Список литературы Моделирование статистических характеристик электромагнитного поля апертурной случайной антенны
- Маслов О.Н. Случайные антенны: теория и практика. Самара: Изд-во ПГУТИ-ОФОРТ, 2013. -480 с.
- Маслов О.Н., Раков А.С., Силкин А.А. Статистические характеристики поля решетки апертурных случайных антенн//Радиотехника и электроника. Т.58, №11, 2013. -С. 1093-1101.
- Маслов О.Н., Раков А.С., Силкин А.А. Статистические характеристики поля апертурной случай ной антенны с учетом корреляционной связи между ошибками//Антенны. №12, 2012. -С. 3-10.
- Маслов О.Н., Раков А.С., Силкин А.А. Статистические характеристики поля апертурной случайной антенны//ИКТ. Т.10, №2, 2012. -С.64-75.
- Маслов О.Н. Применение метода статистического имитационного моделирования для исследования случайных антенн и проектирования систем активной защиты информации//Успехи современной радиоэлектроники. №6, 2011. -С. 42-55.
- Maslov O.N., Rakov A.S. The Research of Random Antennas Method of Statistical Simulation//Applied and Fundamental Studies. Proc. of the 1-st IAC. Vol.
- October, 2012. St. Louis, USA. -P. 251-256.
- Maslov O.N., Rakov A.S., Silkin A.A. Statistical Simulation of Random Antennas like Development of the Statistical Theory Antennas//Proceedings of the IX International Conference on Antenna Theory and Techniques ICATT'13. -IEEE Ukraine, 2013, Odessa. -P. 53-58.
- Алышев Ю.В., Маслов О.Н., Раков А.С., Рябушкин А.В. Исследование случайных антенн методом статистического имитационного моделирования//Успехи современной радиоэлектроники. №7, 2008. -С. 3-41.
- Маслов О.Н. Устойчивые распределения и их применение в радиотехнике. М.: Радио и связь, 1994. -152 с.
- Маслов О.Н. Возможности и перспективы применения метода СИМ при решении внутренних задач СТА//ИКТ. Т.8, №2, 2010. -С. 8-22.