Моделирование струйных течений при сложных внешних условиях

Моделирование струйных течений при сложных внешних условиях

Разработка схем и оборудования для интенсификации процессов тепло- и массообмена с использованием ВЭР является актуальной проблемой промышленности в настоящее время. Эффективность работы теплоутилизационного оборудования зависит от физикохимических процессов, происходящих в теплоагрегате и утилизационном оборудовании. Эффективность работы теплоутилизатора определяется количеством ВЭР и их потенциалом.

На предприятии «Термометр» г. Клин в цехе установлены две камеры формирования стеклянных шариков. Дымовые газы, уходя из камеры формирования, смешиваются с воздухом цеха и удаляются через зонт.

Уходящие из камеры формирования газы, можно считать свободной струей сжимаемого газа. Струя дымовых газов имеет температуру, отличающуюся от температуры окружающего воздуха. Струя делится на три участка: начальный, основной и переходный. В начальном участке изменение температур, плотностей, массы происходят в пограничном слое струи. Он заканчивается, когда пограничный слой распространяется по всему поперечному сечению струи.

В связи с тем, что движение газа в начальном и переходном участках осуществляется под действием положительного градиента давления, то их можно рассматривать как единый участок. Кроме того, переходный участок имеет незначительную протяженность, по сравнению с основным участком.

Дифференциальное уравнение движение потока в основном участке струи запишется:

5 u    „ 5 u p 5 u 5pu   + p^  = it

5 x      d y     5 y 5 y

p

;

где l – коэффициент струи. Уравнение (1) решалось в координатах:

y

x ; ф = — .

ax

Для пограничного слоя струи в основном участке имеем пять граничных условий:

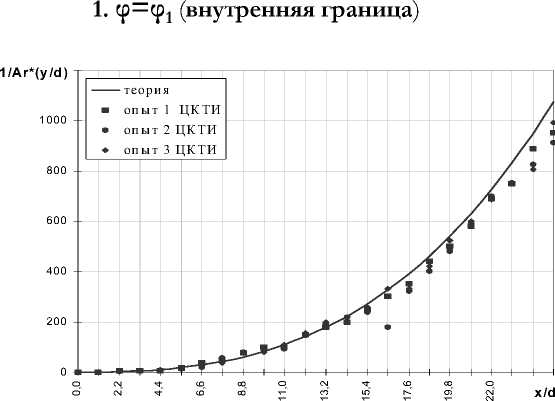
Рис.1. Искривление струи по теореме теплых и холодных струй

• a) ^ = 0,

8ф

• б)    P u = Р 0 ^u Q , в)   P 0^Q = 0.

• 2.    φ=φ₂ ( Внешняя граница ).

  
  

• г)          = 0,

8ф

• д) р и = 0.

Тогда законы изменения скорости, температуры и плотности запишутся как

• ^и = ^и 0 ^х f ( Ф ),
  
  T = T 0 Х0 ( ф ),                                           (3)
  р = р ^хХ( ф ).

После преобразований получим решение системы дифференциальных уравнений. Полученное решение не точно описывает реальный процесс истечения, так как не учитывается искривление траектории движения оси струи вследствие разности плотностей двух сред. Дымовые газы, уходящие из камеры формирования, перемешиваются с холодным воздухом, который опускается вниз и выталкивает теплую газовую смесь. По закону сохранения импульса в случае переменной массы, подъемная сила, действующая на теплую массу газовоздушной смеси, имеет вид:

• д p = m дЭ + Эд m. (4)

  

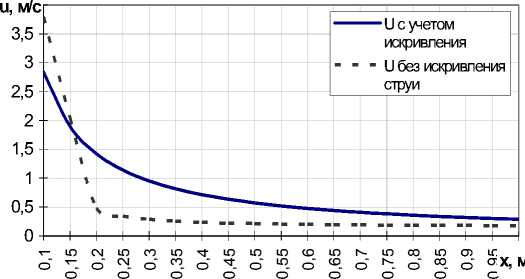
  Рис. 2. Изменение скорости вдоль оси струи с учетом «искривления» струи и без него.

  
  

На рис. 1 представлен график искривления оси нагретой струи при смешении с холодным воздухом и сравниваются с результатами опытов ЦКТИ.

Проведя преобразования, перейдем к безразмерным величинам, получаем уравнения для скорости вертикального «всплытия» теплой струи:

Э

ku cp 2

г дx

C -J

После решения дифференциального уравнения (4) получим искривление траектории струи:

y = 0,36 X K ( x ³ - 0,86 X x ) .                                 (6)

Струя, истекающая из камеры формирования, является двухфазной. На пыль действует большая сила тяжести, чем на газовоздушную смесь. Если в начальном участке струи пыль имеет скорость равную скорости струи, то в основном участке скорость пыли падает и она начинает тормозить газовоздушный поток. Поэтому закон изменения скорости двухфазной струи запишется:

u_m

u

1 + x 0 — u ₀

u ₀

ax R

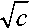
На рис. 2 показаны изменения скорости вдоль оси струи для процесса истечения с учетом искривления струи и наличия примесей и для процесса без искривления. Для определения адекватности модели истечения рассчитаем поля скоростей и температур в различных сечениях струи. Распределение скоростей в сечении определим с помощью формулы Маттиоли:

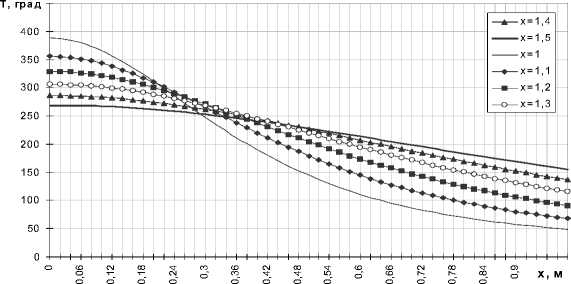
Рис. 3. Температурные поля струи в различных сечениях.

На рис. 3 приведены результаты численного моделирования полей температур в различных сечениях струи и сравнение с результатами опытов Эйлера и Фертмана.

Выводы:

• 1.    Разработана математическая модель процесса истечения нагретой струи в холодное пространство с учетом физических особенностей происходящих процессов переноса в реальных условиях и проведен численный эксперимент.

• 2.    Результаты расчета с помощью математической модели сравнивались с экспериментальными данными. Анализ полученных результатов показал их хорошее согласование.