Моделирование структурного шума, возникающего при контакте рельса и колеса

режения-сжатия (как шарового тензора) над волнами сдвига (как девиатора), т.е. в данном частотном диапазоне свойства воздуха как сплошной среды существенно не влияют на характер её деформирования.

Реализованная в САПР типа ANSYS методика расчёта связанных виброакустических задач методом конечных элементов (МКЭ) является полуаналитической и основывается на поршневой аналогии. При решении вначале определяются перемещения узлов конечномерной модели совокупности поверхностей рельсов, колёс, затем, элементы последних, представляются акустическими поршнями – источниками звука, образующими поршневую группу [1]. Считаем, что в результате воздействия колеса, как сосредоточенной массы на рельс, как стержень происходит прогиб стержня-рельса в вертикальной плоскости, а так же, из-за конической поверхности катания колеса, происходит изгиб рельса в горизонтальной плоскости. От воздействия колёсной пары, рельсы, как бы раскрываются. Кроме того, происходят ударные нагрузки, в силу отклонений поверхностей катания рельса и колеса от идеальных поверхностей. Поскольку процессы изгиба и восстановления протекают в динамике, поезд-то двигается, то перемещающиеся поверхности рельса и колеса мы представляем, как распределённые элементарные поршни (источники давления) создающие в каждой точке воздушного объёма звуковое давление. Полное давление определяется формулами логарифмического суммирования. Эти формулы являются статистическими и хорошо работают только при сравнитель- но большом числе длин волн л на длине свободного пробега, т.е. выше частоты fд. Последняя связана с объёмом замкнутого пространства Vизве-стным соотношением Майера [4].

2.    ПОСТАНОВКА ЗАДАЧИ

Задачи анализа шума, излучаемого при работе различного рода конструкциями относятся к классу сопряжённых задач. Подвижные элементы деформируемых конструкций находящиеся в контакте с воздушной средой, воздействуют на неё, создавая в ней возмущения различной физической природы. В зависимости от уровня энергий силовых воздействий передаваемых сопряженной среде, задача делится на ряд подзадач. Определяющей или первостепенной задачей является достоверное знание динамики поведения твердой сплошной среды, в данном случае конструкции. В настоящее время такая задача достаточно эффективно решается расчётными комплексами САПР типа ANSYS.

Второй задачей является анализ явления распространения шума в воздушной среде.

Эффективные упругие постоянные воздушного объёма определялись исходя из общих положений механики сплошных сред и эксперимента, а соответствие между интенсивностью напряжений в объёме и звуковым давлением устанавливалось из условия равенства энергий деформирования.

22 p __₌ ^a инт

2 pc 2 ■ 3 G '

В выражении (1) 3 G – арктангенс угла наклона обобщённой диаграммы деформирования [7], для близких к несжимаемым материалам, практически совпадает с модулем продольной упругости E . Очевидно, что соотношение (1) справедливо и для пороговых значений p ₀ и σ инт ₀ . Таким образом, можно найти σ инт ₀ и определять УЗД стандартным способом по состоянию напряжённо деформированного поля:

L = L a

= 20lg

/'           A

^a инт CT V ^{a инт} 0 7

Помимо расчёта по формуле (1), УЗД определялись по значениям виброперемещений в воздушном объёме при моделировании его объёмными КЭ:

L = L «

^{= 20l} g Г),

V ^u 0 7

где пороговое значение u ₀ = 8 пм .

При этом нужно отметить то, что в общем случае процесс распространения возмущений в кон- тактируемых средах состоит из ряда явлений. При мощном энергетическом воздействии возмущения могут передаваться в дозвуковом, околозвуковом и сверхзвуковом диапазонах скоростей рассматриваемой среды. Для ограниченных сред критерием выбора метода расчета является сопоставление периода собственных колебаний ограниченной среды с продолжительностью нагружения (длительностью изменяемой нагрузки). Считается, что при длительном во времени нагружении возмущения проходят плавно, квазистатически, поэтому деформирование успевает распространиться на весь объем ограниченной среды и происходит со скоростью её звука. Для неограниченной среды окончание процесса определяется обнулением энергии деформирования среды, после которого начинается процесс образования упругих волн. В околозвуковом и сверхзвуковом режимах возмущения вступают во взаимодействие с собственными амплитудно-частотными характеристиками сред. При этом их энергетическая насыщенность определяется низшими частотами. По мере роста частот энергия акустического явления пропадает.

Таким образом, совместный анализ указанных явлений сводится к определению напряжённо-деформированного состояния системы взаимосвязанных контактирующих упругих сред неограниченное воздушное пространство – ограниченная твердая среда (конструкция) при квазистатическом нагружении (в диапазоне до 300 Гц). И при анализе явлений свыше 300 Гц – динамической задаче напряжённого состояния конструкции состоящей из набора деформируемых элементов (поршней) контактируемых с неограниченным воздушным пространством и излучающих поверхностью контакта акустические волны [1].

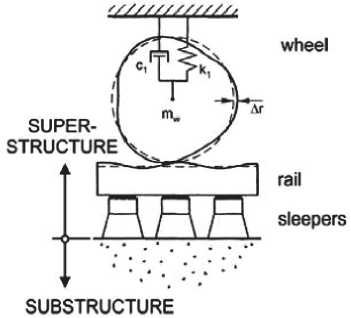
Вертикальные силы от колес к рельсам приложены статически (не перемешаются вдоль пути). Но величина сил определяется с учетом динамики. Она складывается из статического давления колеса на рельс и динамических добавок, возникающих при колебаниях кузова и нео-брессоренных масс подвижного состава при наличии несовершенств пути и колес. В расчет принимается вероятное значение суммарной вертикальной силы.

P вер= P ст+ ( P р+ P ип+ P ик). (4)

При известной статической силе Р _ст (давление от колеса) задача сводится к определению динамических добавок (инерционных сил Р , Р _ип, Р_ик).

Приведенные в работе [6] исследования показывают, что на динамические нагрузки, действующие на путь, существенно влияют качество пути и отклонения колес от формы окружности. Так, при плохом качестве путей, максимальные

б)

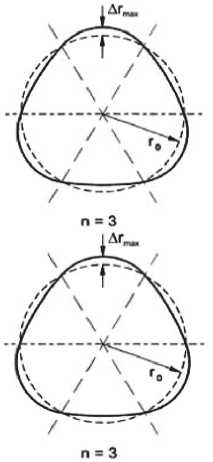
Рис. 1. Нарушение округлости формы колес:

а – отклонение формы колес от окружности 3-й и 4-й степеней; б – идеализированная модель “поезд– рельс–основание” с учетом отклонения формы колес от окружности [6]

динамические усилия могут превысить среднюю квазистатическую осевую нагрузку в два раза при скорости v = 100 км/ч и примерно в 2,5 раза при v = 300 км/ч. Дефекты рельсов и колес также могут привести к нагрузкам, в три раза превышающим нормальную статическую нагрузку на колесо. Такие большие нагрузки всегда связаны с высокочастотной вибрацией.

Одним из факторов, который следует учитывать, является нарушение круглости колес, что в основном случается на высокоскоростных поездах. Это снижает ходовую устойчивость, безопасность и удобство поездки; приводит к увеличению затрат на техническое обслуживание колес и железнодорожных путей. Особо ощутимы для обычных поездов частоты от 50 до 150 Гц, при которых развивается отклонение формы колес от окружности 3…5-й степеней (рис. 1). Такое отклонение вызывает колебания величин нормальных контактных сил, что способствует местному перенапряжению элементов поезда и рельс и усиливает их износ.

В целом, вибрации, возникающие вследствие воздействия динамических нагрузок от поезда, вызывают вертикальное смещение основания путей, которое зависит от осевых нагрузок и скорости поезда; динамических характеристик поездов; взаимодействия между колесом и рельсом и поддержки рельс; характеристик насыпи и надземных конструкций, а также свойств грунта (в том числе, уровня грунтовых вод).

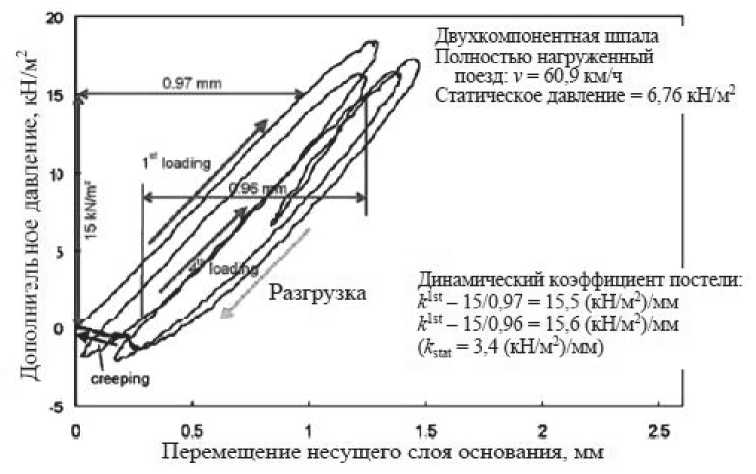
Кроме того, представленные в работе [6] примеры (рис. 2) показывают большую зависимость динамических модулей реакции основания от скорости движения. В обоих случаях железнодорожные пути располагались на двухкомпонентных шпалах, положенных на мощеное основание без балласта, причем величины статического давления и циклы нагружения были одинаковыми.

Таким образом, для формирования расчетной физико-математической модели – расчетной схемы для решения методом конечных элементов требуется достаточно полное всестороннее исследование как уровня нагружения, характера вибрации, так и достаточно трудоемкого изучения физико-механических свойств грунтов дорожного основания.

Для выполнения расчетов формируется общая компоновочная схема (рис. 3) на которой приведены основные элементы конструкции, взаимодействие которых между собой и воздушной средой создают звуковое давления в точках 1-6 экспериментально измеренных показателей уровня шума.

Очевидно, что основными источниками шума в ближних точках 3-4 являются деформирующиеся колеса колёсной пары железнодорожных тележек и рельсы. Наличие железобетонных шпал и грунтового основания демпфируют взаимодействие этой пары и, в какой-то степени гасят энергию колебаний на низких частотах.

Основные технические сведения элементов конструкции – как излучателей звука, необходимые для составления численной расчетной модели взяты для стандартного рельса Р65. Характеристики грунта – нормативные значения модулей деформации Е, кгс/см2, значения физико-механических характеристик взяты по СНиП II-15-74 и СНиП II-53-73.

Для расчёта в качестве нагружения пути был взят универсальный крытый вагон модели 11-217

а)

б)

Рис. 2. Зависимость “напряжение–прогиб” для плиты основания железнодорожного пути без балласта при скорости движения: а - v = 5,3 км/ч; б - 60,9 км/ч

предназначенный для эксплуатации по железным дорогам СНГ с шириной колеи 1520 мм. Для основных типов вагонов железных дорог России осевая нагрузка в настоящее время ограничена величиной 228—245 кН (23,25—25,00 тс). Длина платформы и полувагона кратна величине 6,6— 6,7 м. ширина - 2170 мм. Большинство вагонов грузовых типов подвижного состава эксплуатируются, как правило, на двухосных тележках модели 18-100. Расстояние между осями колёсных пар в тележке грузовых вагонов 1850 мм, а у рефрижераторных вагонов 2400 мм, но оно редко встречается, поэтому примем стандартным расстояние 1850 мм.

По расчетным схемам (рис. 1-3) и справочным сведениям, изложенным ранее с учетом наиболее неблагоприятной возможной деформации колеса тележки относительно пятна контакта с рельсом реализована представленная на рис. 7 конечно-элементная схема.

Конструкции в сборе находится в контакте с воздушным пространством, включающем требуемые точки, для которых были получены экспериментальные значения по шуму. При движении на поперечной оси (относительно продольной плоскости вагона) размещены на буксах два колеса находящиеся в контакте с рельсами. При этом верхняя точка колеса совершает эллипсо-

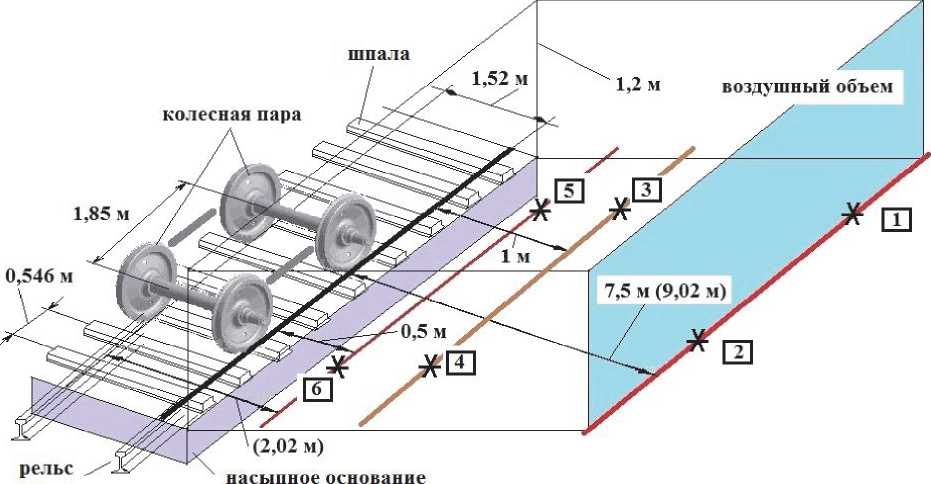
Рис. 3. Расчетная схема 1. Расположение основных элементов конструкции.

Геометрические размеры и расстояния до точек измерения 1-6

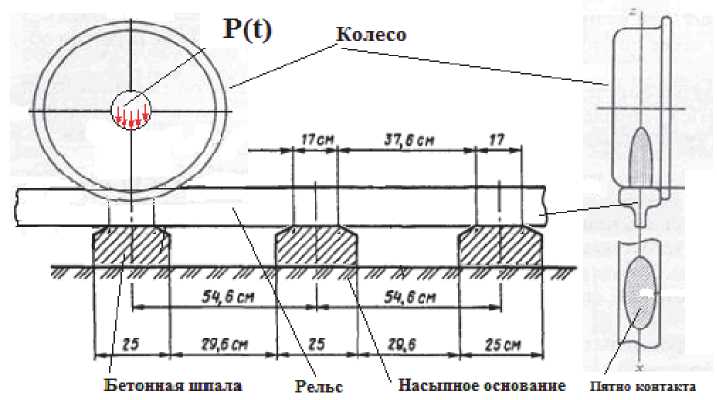
Рис. 4. Расчетная схема 2а

идные вращения по случайной траектории, так как пятно контакта также меняет свою площадь и её конфигурацию, в силу несовершенств поверхности рельса и колеса. Поэтому правильным назначением граничных условий наиболее приближенным к образованию подобных деформаций является закрепление колеса относительно срединного сечения вагона (ограничением его смещения вдоль оси и вдоль продольной линии вагона), что и показано на рис. 7, одновременно с возможностью его деформирования по вертикальному направлению от приложенной силы, действующей на ось. Рельс крепится к поверхности шпалы только по нормали к поверхности. Промежуток рельса между шпалами наиболее подвержен продольно вращательному, колебательному движению. При размещении колесной пары в таком промежутке энергия деформирова- ния является наибольшей по амплитудным колебаниям. Именно такая конструктивная схема и представлена на рис. 7.

Граничные условия для поверхностей воздушного объема показаны на рис. 8. Конечно -элементные сетки срединного сечения представлены на рис. 9 и на рис. 10 разбиение на элементы в крайнем заднем сечении выделенного пространства конструкции (рис. 7).

В расчётной схеме были учтены элементы из стали (модуль продольной упругости E = 210 ГПа , коэффициент Пуассона V = 0,3 , плотность р = 7800кг/м³ , скорость звука c = 5029 м/с² ), воздушный объём ( р = 1 кг/м³ , c = 340 м/с² ), а также из бетона (модуль продольной упругости E = 36 ГПа , коэффициент Пуассона V = 0,16 , плотность р = 2460 кг/м ) и из щебня и песка (модуль

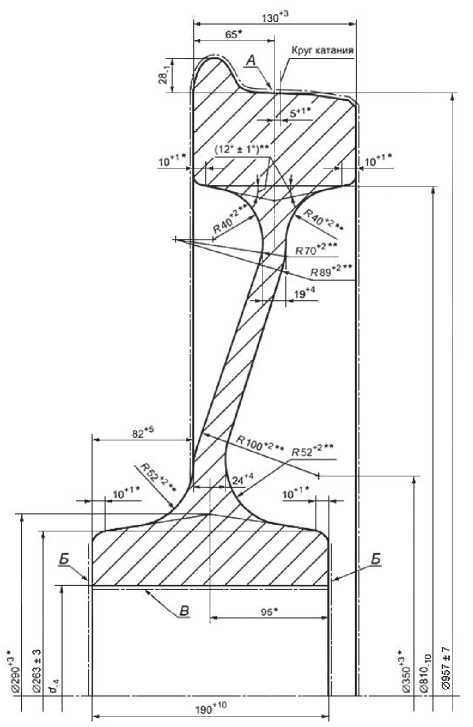
Рис. 5. Колесо стальное цельнокатаное с плоскоконическим диском диаметром

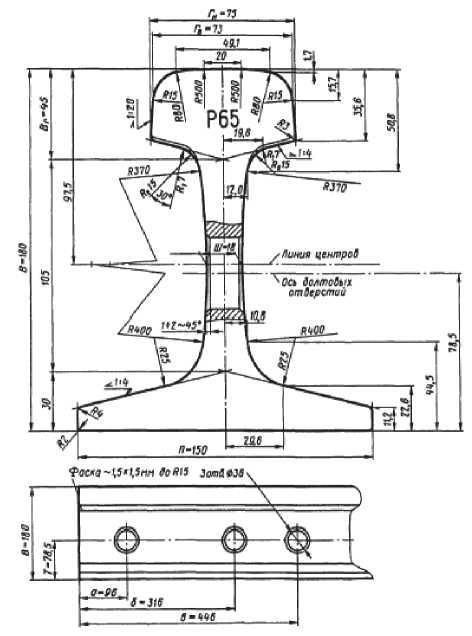
Рис. 6. Основные размеры рельса типа Р65

по кругу катания 957 мм

Рис. 7. Конструкция и воздушный объем МКЭ. Слева сечение продольной симметрии вагона.

Размеры 1795 X 1092 х 2055 мм

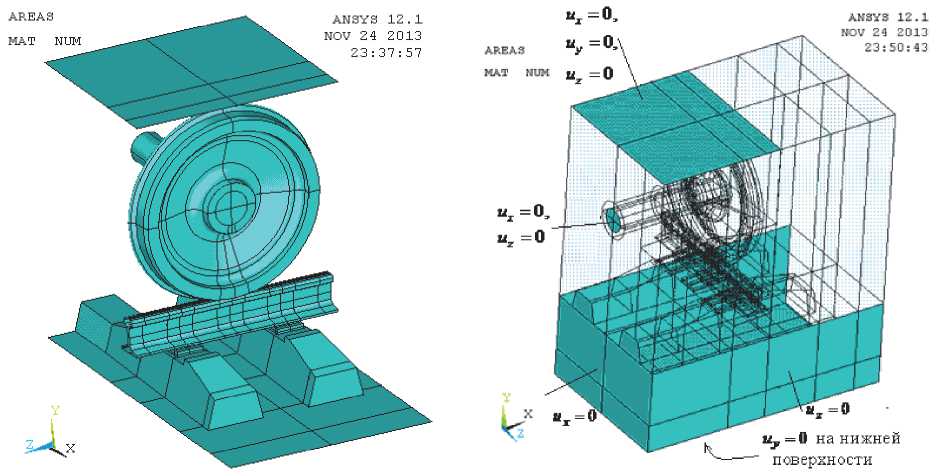
Рис. 8. Поверхности, на которых импеданс равен 1, показаны на рисунке слева; поверхности с принятыми в расчёте условиями закрепления показаны на правом рисунке

ELEMENTS

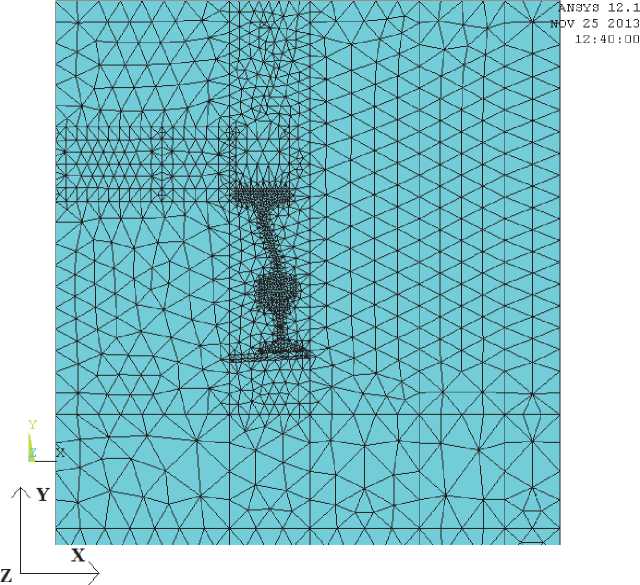
Рис. 9. Сетка конечных элементов в среднем сечении объёма (через центр колеса). Размеры конечных элементов 15…80 мм

продольной упругости E = 5,5 ГПа , коэффициент Пуассона V = 0,25 , плотность р = 2600 кг/м³ ).

Нагрузка, в виде сосредоточенной силы величиной до Рмах=130000 Н, приложена к колесу рядом со ступицей в виде треугольного импульса (рис.11). Вначале она растёт от нулевого значения до 130000 Н за tн=0,01 сек., затем, за такое же время снижается до нуля. Тем не менее, про- цесс деформирования при таком динамическом нагружении сопровождается последействием. Поэтому в последующее время длительностью t=0,01 сек (до 3tн, рис. 11) процесс расчёта продолжается, несмотря на то, что нагрузка не действует. Конструкция после нагружения продолжает совершать свободные колебания вокруг положения статического равновесия. Промежуток времени равный 0,01 сек. соответствует времени,

ELEMENTS

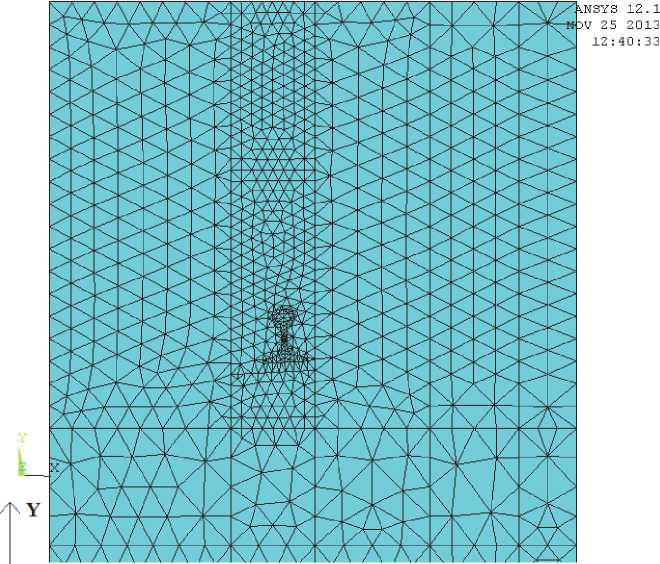
Рис. 10. Сетка конечных элементов в крайнем сечении. Размеры конечных элементов 15…80 мм

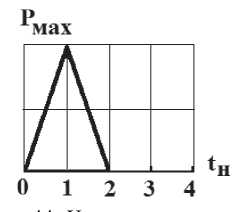
нагружения

. .

за которое колесо на скорости 100 км/час прохо- дит путь ориентировочно равный половине расстояния между двумя шпалами.

Реальный процесс нагружения является незатухающим, такие импульсы повторяются непрерывно, вследствие движения колеса по шпалам. Более точный расчёт нужно проводить методом Фурье (сложения форм колебаний). Однако для предварительного анализа возможностей МКЭ предлагаемый подход правомочен. В данном случае отклик (динамическая реакция конструкции) происходит во всём диапазоне собственных частот конструкции. Следовательно, вычисленная величина звукового давления является суммарной, поэтому её можно сравнивать с экспериментально измеренным суммарным значением для всех частот.

3.    РЕШЕНИЯ И РЕЗУЛЬТАТЫ

Вычисления проводились методом конечных элементов в программном комплексе ANSYS

Multiphysics версии 14.5 на сетках акустических КЭ с линейными функциями формы FLUID30 для воздушного объёма и твердотельных типа

SOLID45 для элементов конструкции соответ ственно. Расчётный объект имеет сложную гео

-

метрическую форму, поэтому он разбивался на тетраэдрические и треугольные КЭ (для FLUID30 – вырожденная форма). Таким образом, был выделен главный параметр – свойства материала и тип элемента, а все второстепенные оставались неизменными, для корректности сопоставления.

На рис. 12 приведены поверхности равного звукового давления в объёме, Н/м2. Слева от надписей (и на других рисунках 13-20) значения переведены в децибелы SMX=112,2 дБ; SMN=106,8 дБ; А=105,37 дБ; В=101,26; Е=99,4 дБ.

4.    ЗАКЛЮЧЕНИЕ

Проведённые расчёты показали хорошую сходимость с данными эксперимента. Наибольшие значения суммарного звукового давления наблюдаются вблизи ожидаемых зон. По мере удаления уровни звукового давления падают. Особое внимание следует обратить на согласование физико-механических свойств расчетной модели конструкции. Для выделения акустических воздействий на октавных частотах следует использовать более быстродействующие ЭВМ.

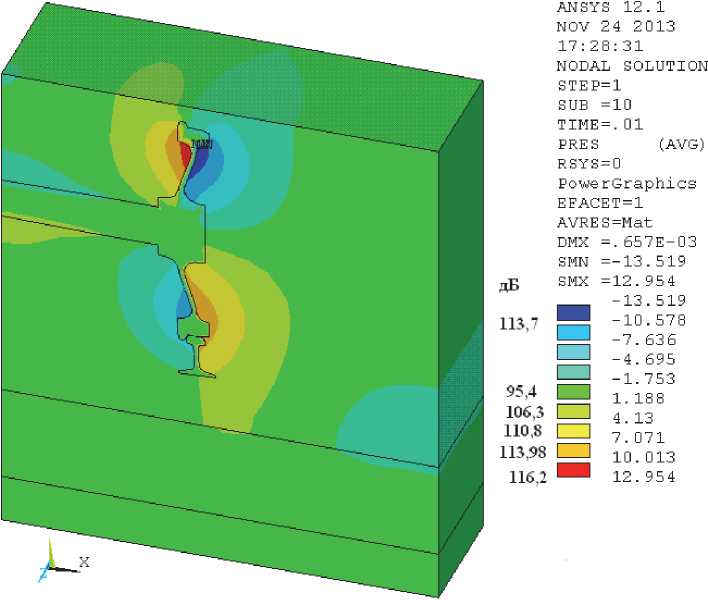
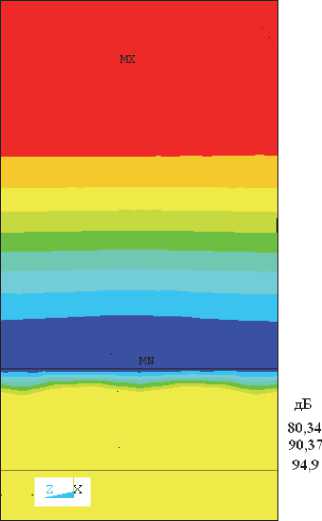
Рис. 12. Поверхности равного звукового давления в объёме, Н/м² (слева в дБ)

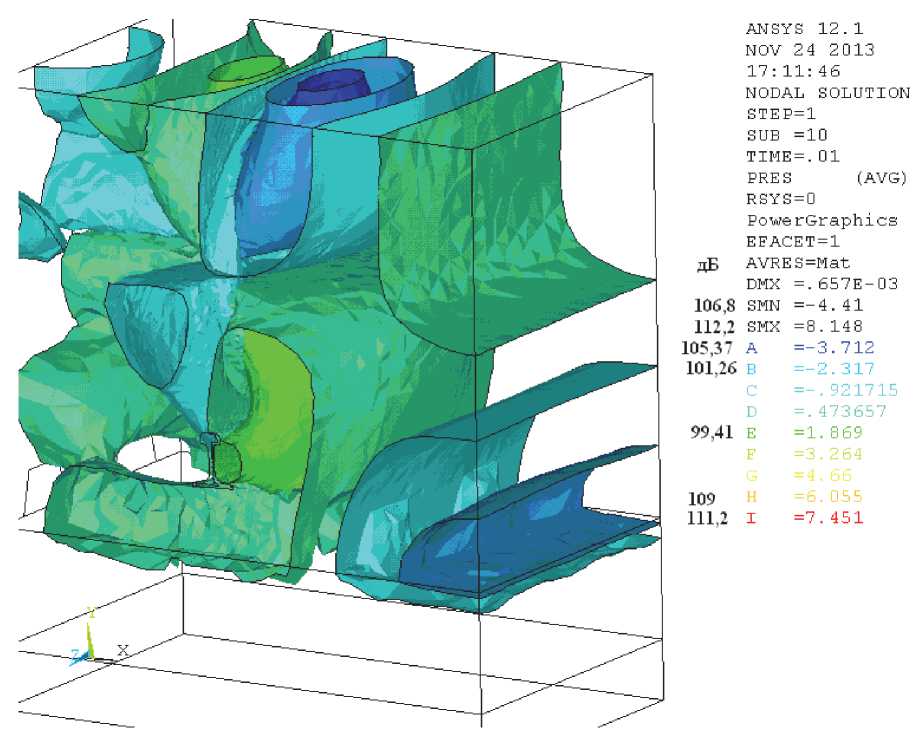
Рис. 13. Поверхности равного звукового давления в объёме, Н/м² (слева в дБ)

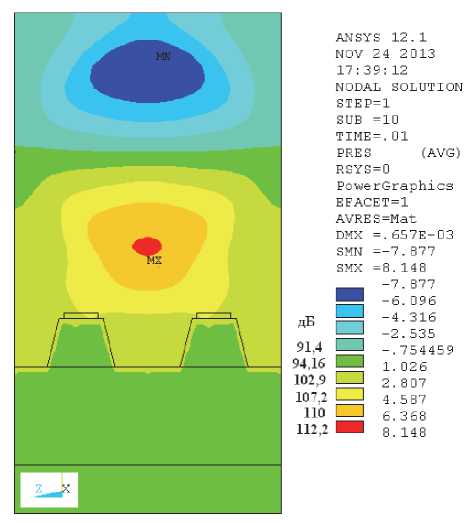
Рис. 14. Распределение звукового давления в по-перечном сечении объёма на расстоянии 0,11 м от головки рельса, Н/м² (слева в дБ)

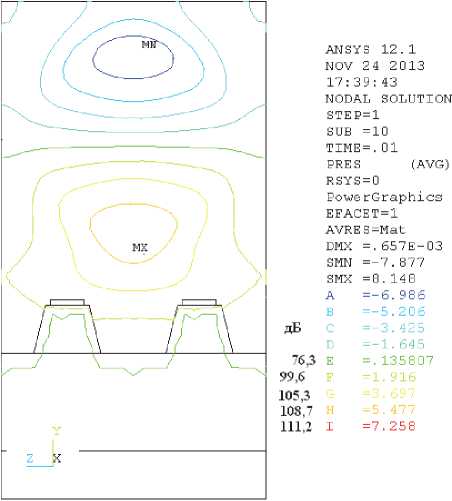
Рис. 15. Распределение звукового давления в поперечном сечении объёма на расстоянии 0,11 м от головки рельса, Н/м² (слева в дБ)

Рис. 16. Распределение звукового давления в поперечном сечении объёма на расстоянии 0,5 м от головки рельса, Н/м² (слева в дБ)

ANSYS 12.1 NOV 24 2013 18:32:04

NODAL SOLUTION

STEP=1 SUB =10 TIME=.01

BRES

RSYS=O

(AVG)

PоwerGraphics

EFACET=1

AVRES=Mat

DMX SMN SMX

=.146E-04

=-2. 9.5 4

=1.112

• - 2 . 9.5 4

• - 2.502

• - 2 . 05

• - 1.5 9 9

  -1.147

  -.694873

  -.243055 .208762 .660579

1. 112

Рис. 17. Распределение звукового давления в поперечном сечении объёма на расстоянии 1,0 м от головки рельса, Н/м² (слева в дБ)

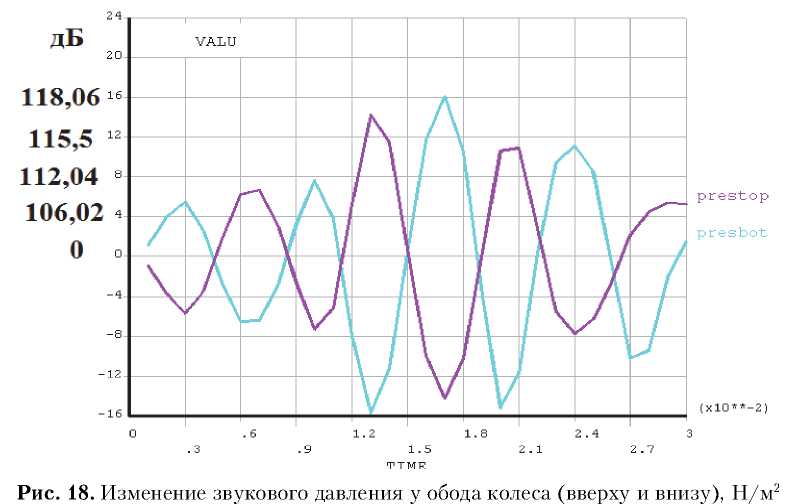
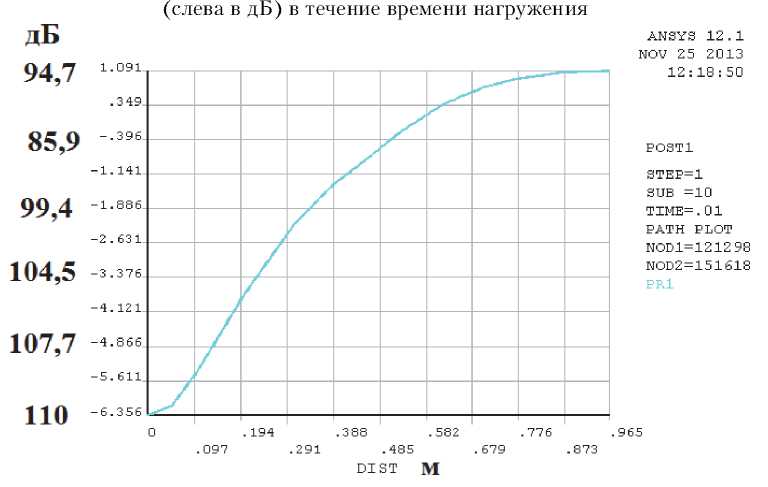
Рис. 19. Распределение давления по мере удаления от колеса на уровне верхнего края, Н/м²(слева в дБ)

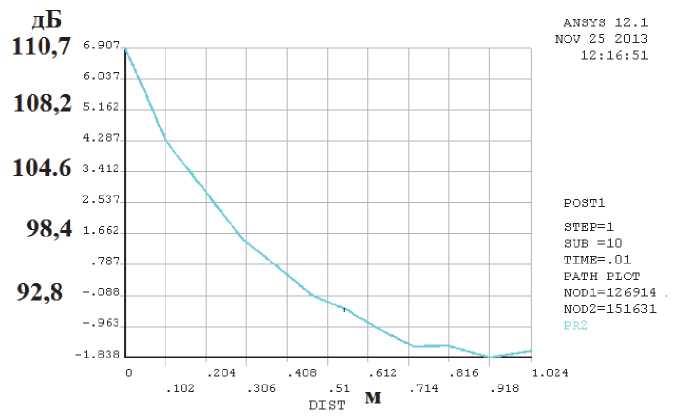
Рис. 20. Распределение давления по мере удаления от колеса на уровне нижнего края, Н/м² (слева в дБ), расстояние равно 1,024 м согласно сетке.