Моделирование структуры потока за стабилизатором пламени методом крупных вихрей

Рис. 1. Обобщенные геометрические характеристики крутоизогнутых отводов вводится во внутреннюю полость трубной заготовки [2].

Для разработки методики проектирования процесса формообразования тонкостенных крутоизогнутых отводов, необходимо определить напряженно-деформированное состояние заготовки и определить особенности деформирования заготовки в данном процессе.

Очаг деформации при проталкивании трубной заготовки имеет сложный нестационарный характер. Изменяются его границы и граничные условия. Напряженно-деформированное состояние заготовки изменяется как во времени, так и при переходе от точки к точке. Большинство существующих до настоящего времени методик анализа формообразования элементов трубопроводов направлены (в основном) на определение энергосиловых параметров процесса [4]. Они не позволяют установить особенности деформирования заготовки без грубой схематизации процесса.

В настоящей работе предлагается методика

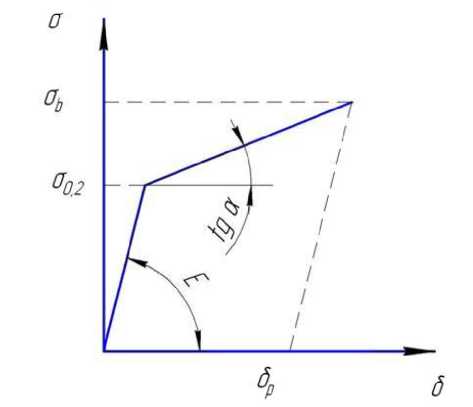
Рис. 2. Билинейная кривая упрочнения определения параметров процесса формообразования крутоизогнутых деталей из трубных заготовок проталкиванием заготовки на основе моделирования данного процесса при помощи метода конечных элементов.

Способность метода конечных элементов решать сложные задачи механики при изменяющихся краевых условиях и нелинейном напряженно-деформированном состоянии дает возможность достоверно проанализировать поведение заготовки при формообразовании крутоизогнутых отводов.

Для моделирования процесса формообразования в выполняемых исследованиях использован конечно-элементный программный продукт – ANSYS-LS/DYNA [5]. Поведение материала заготовки описывается билинейной кривой упрочнения (рисунок 2). Модель материала оснастки (пуансона (толкателя), наполнителя и матрицы) - Rigid Material (твёрдое тело).

Для моделирования деформируемой заготовки выбран элемент SHELL 163 – оболочечный элемент с 4 узлами, возможностью изгиба и пру- жинения. Элемент имеет 12 степеней свободы в каждом узле. Геометрия оснастки и заготовки построена в CAD-системе КОМПАС-3D V8 с последующим импортированием в ANSYS/ LS-DYNA.

С целью получения достоверных результатов анализа, весь процесс формообразования разбивается на достаточно малые стадии и в пределах каждой стадии выполняется определение напряженно-деформированного состояния по всему объему заготовки. При переходе от стадии к стадии накопленные деформации и интенсивность деформации сохраняется для расчета на последующей стадии. На рисунке 3 показаны отдельные стадии процесса моделирования формоизменения.

Размер конечно-элементной сетки существенно влияет на результаты анализа. Более мелкое разбиение даёт лучшие по точности результаты. Однако аппроксимация модели большим количеством мелких элементов приводит к системе алгебраических уравнений большого порядка, что сказывается на скорости выполнения расчёта.

В табл. 1 показано влияние величины параметров сетки и скорости деформирования на результаты анализа при конечно-элементном моделировании процесса формообразования отвода.

В результате анализе использована сетка конечных элементов из четырехугольных элементов, имеющими размеры Li=6мм.

Построение сетки конечных элементов представлено на рис. 4.

3D-модель заготовки после формообразования показана на рис. 5.

Для определения опасного сечения заготовки при формообразовании отвода В результате анализа процесса формообразования крутоизогнутого отвода становится возможным определить деформированное состояние заготовки и деформации изменения толщины по поверхности детали. Данные об изменении толщины и действующих напряжений выводятся с помощью цветовой шкалы и приведены на рис. 5.

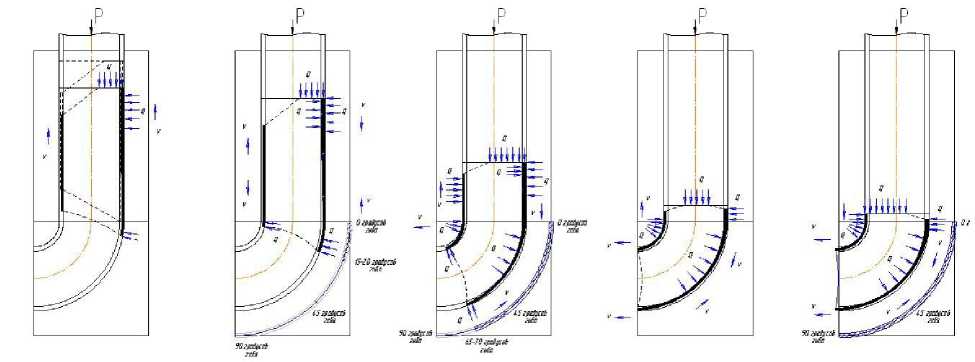
Рис. 3. Моделирование по стадиям формообразования крутоизогнутого патрубка

Таблица 1. Влияние параметров моделирования на результаты анализа

Изменение размеров ячейки координатной сетки

Интенсивность деф ормаций

Изменение скорости перемещения пуансона

Зн ачение толщины в узлах в зависим ести от изм ененных парам етров сетк и

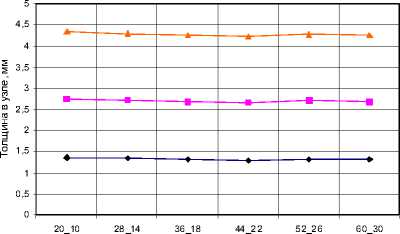
П араме тров сетки, D/Rг

RminТу —■—RminТв -*—RmaxТв

Зн ачен ие толщины в узлах в зависимести от изм енен ия скор ости деформ ир ован ия

5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0

100         300         500         700         900        1100

Скорость деформ ирования , мм/с

Интенсивность нап ряжени й

Зн ачени е интенсивности нап ряж ений в узлахв в зависим ести от изм ененн ых параметров се тк и

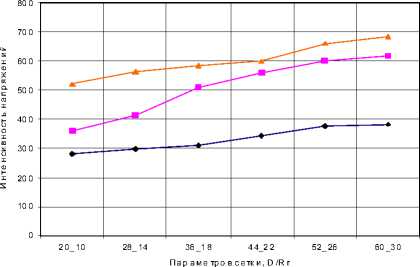
RminТу ■ RminТв * RmaxТв

—♦—RminТу ■ RminТв    RmaxТв

Значение интенсивности напряжений в узл а хв в зависимести от изменения скорости де фо рм ир ова н ия

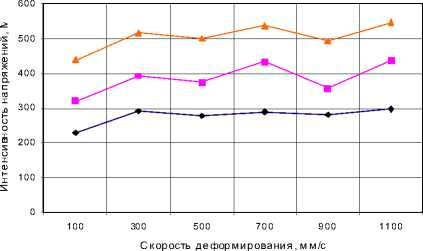
—♦— Rm inТу —■ RminТв —*— Rm axТв

Толщина заготовки

З начение интенсивности деформ аций в узлах в зависим ести от измененных п арам етр ов сеткм

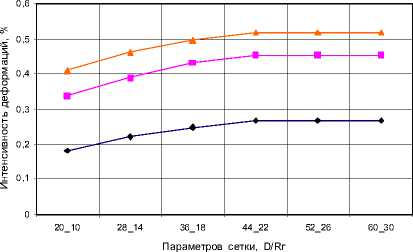
RminТу ■ RminТв —*—RmaxТв

Знач ение инт енс ив ности деформ аций в узлах в зав исим ест и от изменения скорости деформирования

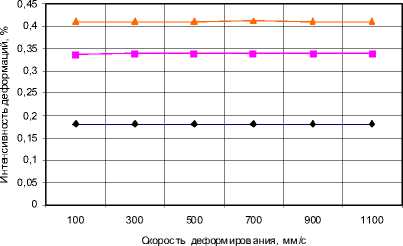
н RminТу —■ RminТв —*— RmaxТв

Результаты исследования деформированного состояния заготовки представлены на рисунке 6. На этих же графиках приведены и теоретические кривые изменения толщины, полученные в результате компьютерного моделирования процесса формообразования отвода с использованием программного продукта ANSIS–LS-DINA.

Установлены следующие особенности деформирования трубной заготовки в штампе предлагаемой конструкции:

• 1.    Максимальное утонение наблюдается на торцах штампованной детали со стороны минимального радиуса гиба детали.

• 2.    Со стороны образующей по максимальному радиусу гиба утонение наблюдается в центральной части деформируемой заготовки.

• 3.    Максимальная разнотолщинность штампованной детали не превышает 24 %.

На рис. 7 показано сравнение экспериментальных значений изменения силы (деформиро-

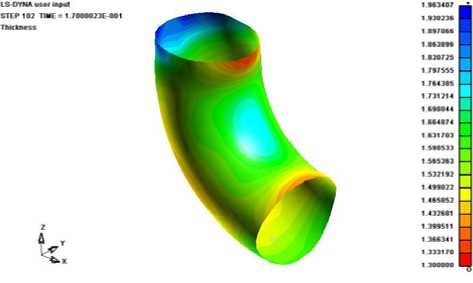
Рис. 5. Характер изменения толщины заготовки, полученный в результате расчета

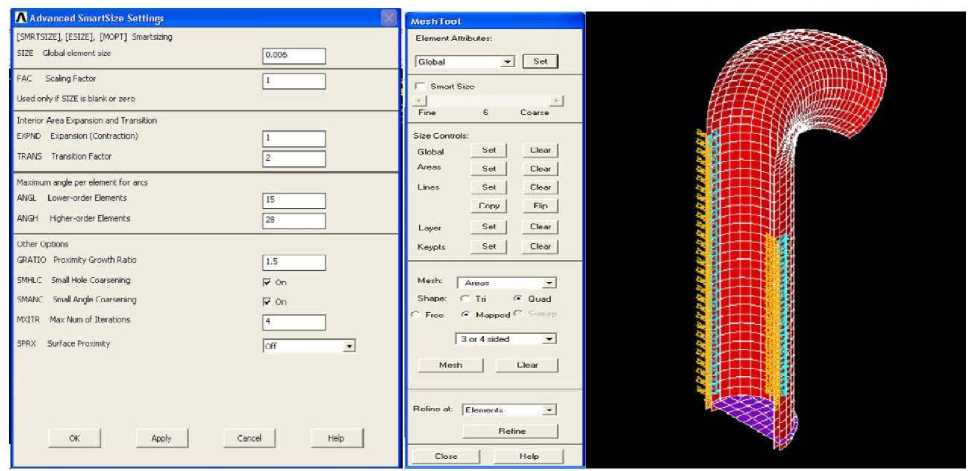
Рис. 4. Построение сетки конечных элементов

вание заготовки диаметром 53мм с толщиной стенки 1,5 мм из коррозионно-стойкой стали 12Х18Н10Т, смазка – машинное масло с наполнителем из графитового порошка) с теоретической кривой, полученной при мо-делировании процесса с помощью программного продукта ANSYS–LS-DYNA.

Характер изменения силы с увеличением хода пуансона позволяет сделать следующие выводы:

• 1.    Сила деформирования максимальна на промежуточных стадиях процесса деформирования.

• 2.    На силу деформирования влияют два фактора, соотношение между которыми в процессе деформирования изменяется: развитие очага деформации на начальной стадии деформирования и сокращение протяженности прямолинейного участка трубной заготовки на заключительной стадии деформирования.

Результаты исследований показали, что после того как сила достигает своего максимума, та часть заготовки, которая уже изогнута, в дальнейшем практически не деформируется. Она

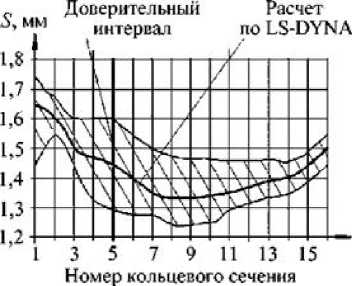
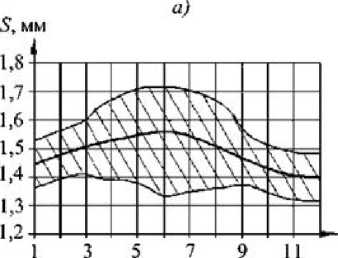
Номер кольцевого сечения 6)

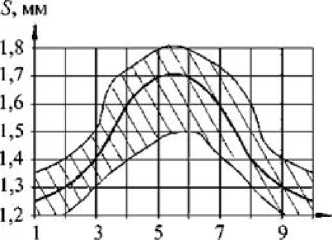
Номер кольцевого сечения в)

Рис. 6. Изменение толщины заготовки в меридиональном направлении: а – R _max ; б – R _ср ; в – R _min

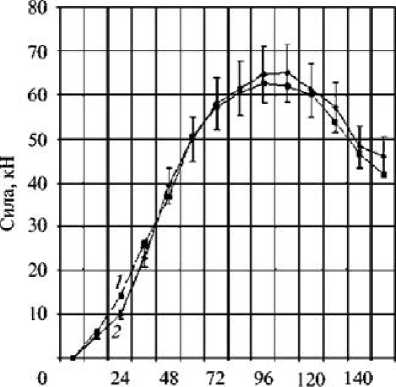
Ход пуансона, мм

Рис. 7. Изменение силы деформирования по ходу процесса

1 – расчет по программам ANSYS и LS-DYNA;

2 – экспериментальные данные лишь преодолевает силы трения, перемещаясь в зазоре между внутренней оправкой и рабочей поверхностью полуматриц.

Для определения опасного сечения заготовки при формообразовании отвода воспользуем-

Распределение предельной степени деформации в меридиональном направлении (по радиусу гиба) Образующая по максимальному радиусу гиба – Rmax

Rmax

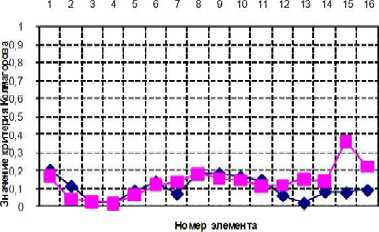
Рис. 8. Разрыв заготовок в опасном сечении при формообразовании отводов ся критерием Колмогорова.

В соответствии с критерием Колмогорова образование трещин происходит при условии когда интенсивность накопленной деформации равна величине критической деформации при данной схеме напряженного состояния

t

∫dεi

ψ = 0     = 1 – критерий Колмогорова;

^ε ρ ^cc

Распределение предельной степени деформации в тангенциальном направлении (по диаметру детали) Образующая на торце, передающем усилие – Tu

Tu

Образующая на выходном торце - Tv

Образующая по минимальному радиусу гиба – Rmin

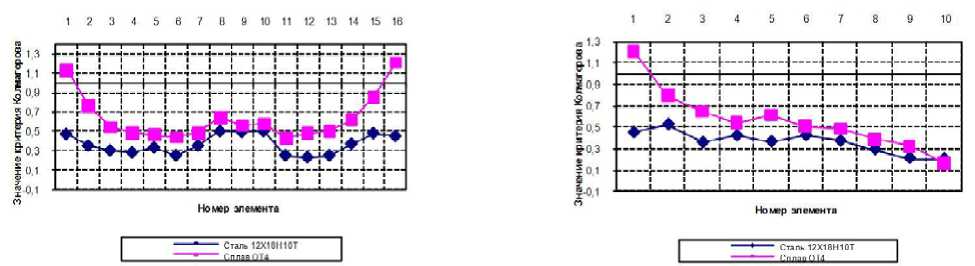
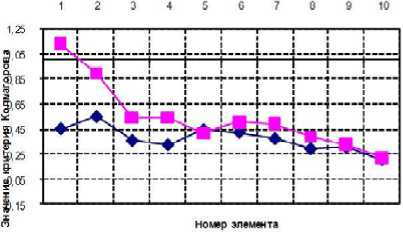
Рис. 9. Графики распределения критической степени деформации (по критерию Колмогорова) в меридиональном и тангенциальном направлениях на заключительной стадии процесса формообразования (угол гиба 90 градусов) для материалов заготовки - сталь 12Х18Н10Т и сплав ОТ4

при ψ ≥ 1 – происходит разрушение материала;

при ψ <  1 - разрушения не наблюдается;

ε _i =

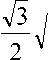
( ε 1 - ε 2 ) + ( ε 2 - ε 3 ) + ( ε 3

ε1)2 – интенсивность деформации;

ερcc = 2δр exp[-2.16 0 ] – предельная сте-σi пень деформации;

ε_ρ = δ_ρ – относительное равномерное удлинение образца;

σ1 + σ2 + σ3

σ0 =             – среднее значение на- пряжений в узле;

σi = 1 (σ1 -σ2)2 +(σ2 -σ3)2 +(σ3 -σ1)2 –ч 2

интенсивность напряжений.

Для расчета предельной степени деформации выбирались элементы в меридиональном и тангенциальном направлениях. В меридиональном направлении по максимальному радиусу гиба, в тангенциальном направлении на торце передающем усилие и выходном торце (рисунок 9). Результаты представлены в виде графиков сравнения предельной штампуемости двух материалов: стали 12Х18Н10Т и сплава ОТ4 на заключитель- ной стадии процесса формообразования (угол гиба 90 градусов).

В результате анализа полученных графиков (рис. 9) можно сделать следующие выводы: при формообразовании отвода из стали разрушение не наблюдается. При этом наибольшая степень предельной деформации возникает на торце, передающим усилие и выходном торце по минимальному радиусу гиба. При формообразовании отводов из сплава ОТ4 возникает разрушение на торцах по минимальному радиусу гиба.