Моделирование свойств материала на стадии разупрочнения

В общепринятом варианте теории упругости используются, как правило, две технические константы изотропного материала: коэффициент поперечной деформации (КПД) v и модуль Юнга E. Оба параметра остаются неизменными как при активном растяжении до предела упругости с y , так и при разгрузке. За пределом упругости при 8 > 8 y разделяют активное нагружение с переменными (касательными, мгновенными) параметрами E p = 5о/58 , v p =-58 '/58 и упругую разгрузку при E u = E , v u = v ; как правило, полагают v p = 0,5, что следует из условия несжимаемости, а изменением модуля разгрузки E_u пренебрегают. Между тем из экспериментов известно, что v _p * 0,5 только в области деформаций предела текучести, а при больших деформациях снижается [1]. Изменение модуля E u при разрыхлении материала достигает десятков процентов [2, 3]. Стадия разупрочнения материала, отражаемая падающей ветвью диаграммы деформирования, в этом плане практически не изучена. Для построения корректной теории разупрочняющихся материалов нужны функциональные зависимости свойств материала от степени деформации при различных видах нагружения.

Рассмотрим предельно простую и легко обсчитываемую физическую модель материала в виде пучка параллельных упруго-хрупких стержней числом m, определяемую следующими соотношениями: - условием совместности деформаций

8 _к =8 , к = 1, m ;

- условием равновесия i m         i m

с=m £ сk (8) f‘= m § °k- где fk = const - площадь сечения стержня, а с к - напряжение в нем; - физическими уравнениями

Го к = E 8 ,0 <8 <8 Вк ,                                    (3)1      0 ,8 >8 Вк ,

где E = const - модуль упругости материала стержней, 8 _Вк - деформация предела прочности стержня с номером к .

Обычно полагается [4], что стержни плотно упакованы и касаются друг друга без надавливания в процессе деформирования. Сохраняя это свойство модели, естественно предположить, что две половинки разрушенного по одному сечению стержня разгрузятся, образуя «пору», и «раздвинут без надавливания» целые стержни. Таким образом, с появлением разрушенных стержней в образце идут два конкурирующих процесса: снижение площади поперечного сечения вследствие вытяжки целых стержней и увеличение площади за счет разрушенных. Меняется соотношение продольных s и поперечных s ' деформаций для пучка в целом. Коэффициент поперечной деформации при дискретном подходе

As '                                               (4)

v = ---- As

становится функцией от степени деформации, что и выражает суть проводимого ниже расчета КПД.

В исходном состоянии геометрически одинаковые стержни диаметром d ₀ и площадью сечения f ₀ перемешаны и плотно упакованы в пучок (образец, испытуемый объем) с квадратным сечением площадью F 0 = md 02 и стороной а ₀ = FF = = mm.d ₀.

Согласно выражениям (3) отдельный стержень остается упругим вплоть до разрушения. Его диаметр убывает при растяжении по закону d = d 0(1 -vs ),(5)

где v = const - коэффициент Пуассона материала стержня.

Вместе с диаметром убывает площадь и сторона сечения образца, появляется поперечная деформация а 0 - a (s)

s ' =.

a ₀

Пока нет разрушенных волокон, имеем

F (s ) = md 02(1 -vs )2,

a(s ) = mmd0 (1 -vs ), а поперечная деформация образца согласно (6) и (7)

s ' = v s,

следовательно, КПД образца остается постоянным и равным коэффициенту Пуассона материала стержня. Не меняют своих значений при разгрузке КПД v u = v и модуль E u = E . Объемная деформация модельного образца совпадает с таковой для сплошного стержня тех же размеров. Сохранение упругих свойств в модельном образце на начальном этапе деформирования можно считать качественным подтверждением правомерности сделанных допущений, поскольку физическая суть деформирования не искажается.

Характер разрушения образца определяется как свойствами его структуры, так и условиями нагружения [5]. Структурная неоднородность в схеме Даниэльса моделируется заданием равномерного закона распределения случайной деформации предела прочности элементов R {s Bа, s Bр}. Поврежденность материала ® при i разрушенных стержнях и деформации s Ba

i

ш = —

m

Нагружение «мертвой» нагрузкой снимает вопрос об устойчивости процесса разрушения и влиянии условий нагружения.

Две половинки разрушенного стержня с номером k разгружаются упруго, без остаточных деформаций. Их диаметр скачкообразно увеличивается от значения d_k = d ₀(1 -ν ε _Bk )

до начального размера d ₀ .

При наличии i разрушенных стержней находится площадь образца с порами, F = ( m - i ) d ₀²(1 -νε )² + id ₀²,                                (9)

а затем определяются сторона a , поперечная деформация ε ' и КПД на стадии повреждения.

Дискретный подход, отраженный в формулах (4)-(9), удобен для машинного счета. В приведенном ниже примере (рис.1) расчет велся с шагом по деформациям

Δε = (ε Bβ- εBα)(m- 1)-1

для конечного числа стержней m . Кроме того, появляется возможность детального исследования поведения пучка стержней при разрушении одного из них.

Полная диаграмма деформирования, рассчитанная по формулам (1)-(3), при достаточно большом числе стержней выглядит гладкой кривой (см. рис.1,а). В увеличенном масштабе или при малом числе элементов зависимость σ ( ε ) пилообразна (вставка, см. рис.1,а). Точками a , b и c отмечены состояния образца перед разрушением отдельного стержня, после разрушения и после активного догружения на величину Δε . По формулам (7), (9), (6) рассчитываются соответствующие значения поперечной деформации ε _a ', ε _b ' и ε _c ' . Таким образом, разрушение каждого стержня приводит к скачкообразному изменению свойств моделируемого материала при неизменной деформации и, как следствие, неоднозначности в определении КПД.

Упругие свойства поврежденного материала ( ε > ε _α ) определяются при разгрузке и повторном нагружении. Так, модуль разгрузки (при i разрушенных стержнях и с учетом (8)) m - i ^{ε -ε}

E = E= Bβ E u m εBβ- εBα линейно убывает до нуля с ростом деформации. КПД разгрузки ν u , определяемый при Δε '=εc'-εb', также линейно зависит от степени деформации (см. рис.1.б, прямая 1),

ν

u

ε Bβ - ε

ν .

ε B β ^- ε B α

Сравнивая два последних выражения, получим

ν _u ( ε ) ₌ E_u ( ε ) ν⁼ E

Равенство (10) указывает на то, что графики зависимостей ν _u ( ε ) и E_u ( ε ), построенные в относительных координатах, совпадают. Кроме того, зная зависимость E_u ( ε ), КПД ν _u ( ε ) для данной модели можно вычислить по соотношению

ν ν _u ( ε ) = E_u ( ε ). E

Упругие свойства образца, найденные при i разрушенных стержнях, сохраняются до разрушения следующего i +1-го элемента. В данной модели активное нагружение по пути b - c идет с КПД ν _u , принимающим только положительные значения и отражающим тот факт, что в пределах догрузки поперечные размеры образца убывают.

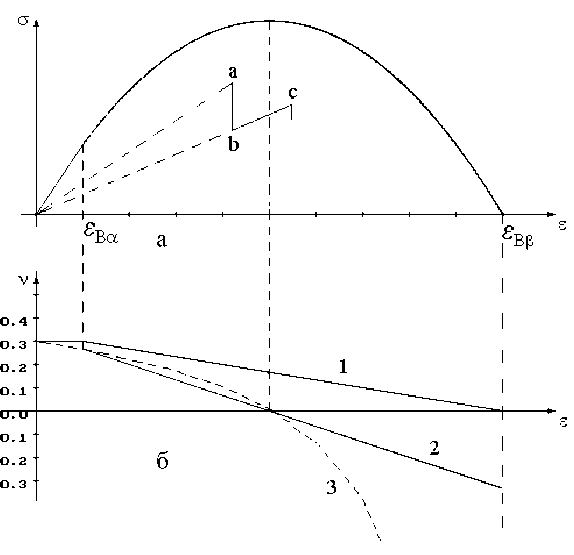
Рис. 1. Модель с хрупкими элементами: а - полная диаграмма деформирования при т= 1000 , E =20000 кг/мм²;

б - коэффициент поперечной деформации

Сравнивая поперечные размеры образца в состояниях c и a , найдем Ав ' = в _c ' -в _a ' и полный (текущий, касательный) КПД v _p (ломаная 2, см. рис.1). Сравнение зависимостей v _p и E p ( в ) = d а/ d г приводит к результату, аналогичному (10) и (11):

^v p^{( в} ) _ E p^{( в} )

v = E ,

ν

v p(в) = 7 Ep(в), что позволяет найти связь введенных параметров v u и v p v u(в ) = v p(в )

E u ( в ) E p ( в ).

Коэффициент v _p может принимать отрицательные значения, отражая тот факт, что при растяжении поврежденного образца его поперечные размеры могут возрастать. Приращения поперечных деформаций меняют знак с некоторого момента, зависящего от степени структурной неоднородности. Величина скачка на графике v _p ( в ) при деформации e _{В а} зависит от соотношения в B _а и в B в , возрастая от нуля при в B _а= 0 и стремясь к бесконечности при в B _а^ в B в при неизменном в B в (кривая 3 на рис.1,б).

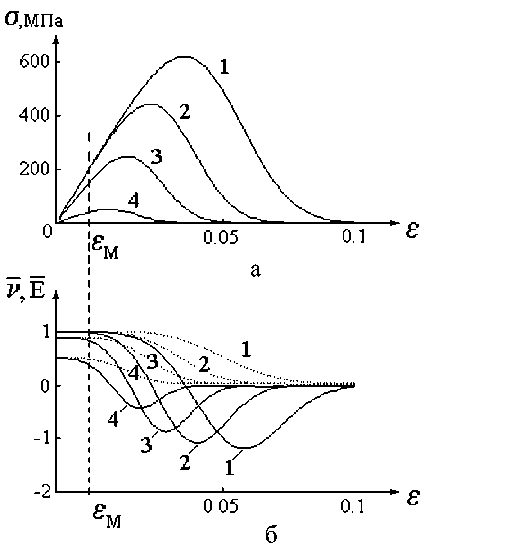
Рис.2 Диаграмма σ ( ε ) –(а) и зависимости изменения свойств пучка при нормальном законе распределения случайной деформации ε _B – (б)

Таким образом, для получения полной информации об изменении свойств материала, описываемого моделью Даниэльса, при одноосном растяжении достаточно иметь диаграмму σ ( ε ) и зависимость E_u ( ε ). Остальные параметры E_p ( ε ), ν _p ( ε ), ν _u ( ε ) рассчитываются. Этот результат остается в силе при любом другом законе распределения случайной деформации предела прочности, хотя сами зависимости существенно изменяются. На рис.2,а и 2,б (кривые 1) приведены диаграмма σ ( ε ) и зависимости изменения свойств пучка при нормальном законе распределения случайной деформации ε _B . Диаграмма σ ( ε ) становится гладкой с точкой перегиба на падающей ветви. Зависимости изменения свойств становятся нелинейными, исчезают скачки в кривых касательных свойств ν _p и E_p .

Как следует из анализа модели, функциональные характеристики материала E ( ε ) и ν ( ε ) должны быть увязаны с диаграммой деформирования. Следовательно, такие факторы, как циклирование, температура, активная среда и т.д., должны влиять на них в той же степени, что и на диаграмму в целом. Например, экспериментально установлено вырождение статической диаграммы ряда конструкционных материалов при циклировании [6]. Изменение зависимостей E ( ε ) и ν ( ε ) при этом не исследовалось.

Дополним уравнения модели (1)-(3) циклическими свойствами стержней при постоянном значении максимальной деформации цикла ε _M = const . Из эксперимента должны быть известны:

• -    «трехсигмовый» интервал ε _{B α} , ε _{B β} нормального распределения предельный деформаций нетренированных стержней (рис.3);

• -    «трехсигмовый» интервал N _α , N _β случайной долговечности стержней при

  _-

  
  

стационарном пульсирующем нагружении с ε M = const ; кинетическая кривая (для примера однопараметрическая), вырождение статических свойств стержней при циклировании отражающая

εBβ(εM,n)=εB0β-kεnα(εM), где kε находится из условия усталостного разрушения наиболее прочного стержня, ε Bβ(ε M,Nβ)= ε M. (13)

Ограничимся областью многоцикловой усталости и положим, что кинетические кривые всех стержней подобны кривой (12). Данное ограничение позволяет найти распределение предельных деформаций при любом фиксированном числе циклов тренировки. Пока нет циклически разрушенных стержней n< Nα , распределение полное, а при n> Nα - усеченное (рис.3). Разброс долговечности стержней при ε M = const обусловлен, таким образом, различным отношением εBεM в исходном состоянии.

На рис.2,а приведены вырожденные кривые σ ( ε ), или циклические диаграммы деформирования (кривые 2, 3, 4), а соответствующие зависимости E ( ε ) и ν ( ε ) в относи тельны х коо рдинатах изоб ражен ы на рис.2, б ( n ₁ = 0, n ₂ < n ₃ < n ₄). Графики E_p ( ε ) и ν _p ( ε ), а также E_u ( ε ) и ν _u ( ε ), построенные после любого фиксированного числа циклов тренировки, по-прежнему совпадают. Следовательно, циклическое нагружение, меняя параметры диаграммы деформирования и функций E ( ε ) и ν ( ε ), не нарушает их взаимосвязи.

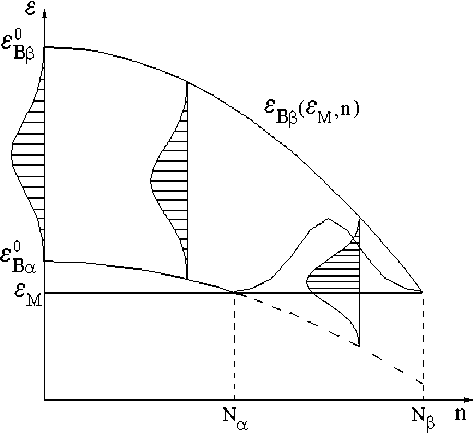
Рис. 3. Вырождение свойств распределения при циклировании образца

Вывод о существовании указанной связи касается только исследованной модели и имеет качественное значение. Установление подобных связей у конструкционных материалов позволило бы сократить число базовых экспериментов, необходимых для совершенствования моделей материала. Полученные результаты позволяют сделать заключение о перспективности использования простейших физических моделей материала для изучения качественных связей его основных характеристик.