Моделирование температурного поля поверхности при электроискровом легировании металлов
Автор: Власенко Виктор Дмитриевич, Иванов Валерий Игоревич, Аулов Вячеслав Федорович, Коневцов Леонид Алексеевич, Мартынова Елена Геннадьевна, Хасан Исмаил Халил
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Физика
Статья в выпуске: 2, 2019 года.
Бесплатный доступ
Введение. В настоящее время особую актуальность приобретает проблема повышения эксплуатационных свойств деталей машин, инструментов и технологической оснастки посредством улучшения физико-химико-механических характеристик их исполнительных рабочих поверхностей. Одним из современных методов получения покрытий на поверхностях деталей является метод электроискрового легирования, при котором важную роль играет выбор теплофизических свойств материалов для получения покрытий с заданными физико-механическими и триботехническими свойствами. С целью выбора материала электрода в статье изложены результаты разработки метода расчета нестационарного температурного поля обрабатываемого материала (катода) в виде прямоугольного параллелепипеда, на одной грани которого в процессе электроискрового легирования формируется легированный слой. Материалы и методы. Для формирования легированного слоя при каплевидном электромассопереносе в качестве обрабатываемого материала (катода) использовалось железо в форме параллелепипеда, а в качестве обрабатывающего материала (анода) - вольфрам. Предложена нелинейная начально-краевая задача и вычислительная схема для определения значений температуры во всех точках температурного поля катода в форме параллелепипеда с расположением нескольких теплоизлуча-ющих капель на его грани. Результаты исследования. В статье изложен алгоритм решения задачи в соответствии со второй формулой Грина для нахождения температурного поля в катоде, имеющем форму параллелепипеда; при этом описанная нелинейная модель потока из капель в параллелепипед заменяется линейной моделью. Построен алгоритм, проведены расчеты для определения значений температуры во всех точках и температурного потока в катоде в случае одной среднестатистической капли на его грани. По данному алгоритму создан пакет программ, проведены экспериментальные расчеты. Показана динамика значений температуры (во всех точках) и теплового потока исследуемых точек катода. Обсуждение и заключение. Результаты проведенных исследований свидетельствуют о том, что для достижения более высоких свойств покрытий и большей эффективности электроискрового легирования необходим расчет температурного поля и теплового потока исследуемых точек катода. Представленная математическая модель получена для нанесения одной капли, помещенной на границу теплопроводящего полупространства. При выборе анодного материала в зависимости от эрозионной стойкости для получения необходимой толщины поверхностных слоев с заданными функциональными свойствами используется разработанный метод расчета, который позволяет описать процесс остывания одной нанесенной капли и использовать затем полученную информацию для усредненного описания эффекта нагрева тела параллелепипеда рядом таких капель.
Электроискровое легирование, анод, катод, температурное поле, легирование металлов, моделирование температурного поля
Короткий адрес: https://sciup.org/147220616
IDR: 147220616 | УДК: 621.9.048.4: | DOI: 10.15507/2658-4123.029.201902.218-233
Текст научной статьи Моделирование температурного поля поверхности при электроискровом легировании металлов
Проблема улучшения эксплуатационных свойств (износо- и жаростойкости, а также коррозионной стойкости) рабочих поверхностей деталей машин, инструментов и технологической оснастки путем улучшения физико-химико-механических характеристик приобретает все большую актуальность. В настоящее время прогресс в машиностроении во многом связан с применением высокоэффективных методов модификации рабочих поверхностей деталей машин, инструментов и технологической оснастки, основанных на использовании потоков энергии с удельной мощностью в пятне нагрева более 102 Вт/мм2. К их числу относится современный наукоемкий метод электроискрового легирования (ЭИЛ). Его достоинствами являются высокая прочность сцепления легированного слоя из любых токопроводящих материалов (в том числе тугоплавких металлов и сплавов) с обрабатываемым материалом, низкая энергоемкость процесса, простота выполнения технологической операции и др. Применение метода ЭИЛ для упрочнения рабочих поверхностей деталей, инструмента и оснастки обеспечивает повышение срока их службы в пять и более раз. В условиях современного машиностроительного производства метод ЭИЛ является востребованным, а его изучение с целью более эффективного использования при получении функциональных покрытий становится актуальным.
Обработка токопроводящей поверхности посредством ЭИЛ представляет собой многоэтапный процесс. Каждый его цикл включает краткосрочный контакт электрода-анода и детали-катода; полярный перенос электродного материала на деталь в зоне действия искрового разряда; микрометаллурги-ческий процесс на ее поверхности с химическим взаимодействием элементов материалов электрода, детали и межэлектродной среды; быстрые разогрев и охлаждение микрообъема поверх-
Vol. 29, no. 2. 2019 ностного слоя детали. Результатом является изменение структуры, химического и фазового составов, а также свойств поверхностного слоя детали и рельефа ее поверхности.
При каждом цикле ЭИЛ на катоде образуется лунка, заполненная материалом, полученным в результате взаимодействия катода, анода и межэлектродной среды [1; 2].
Одним из основных вариантов становится перенос горячей частицы, температура которой близка к температуре плавления, на холодную поверхность, температура которой близка к температуре окружающей среды. В ходе этого вероятно закрепление частицы на поверхности практически без образования зоны взаимной кристаллизации [1].
Для указанного случая в зависимости от эрозионной стойкости материала и получения необходимой толщины поверхностных слоев с заданными функциональными свойствами рассматривается математическая модель определения температурного поля катода.
Обзор литературы
Многие ро ссийские и зарубежные исследования посвящены использованию метода ЭИЛ при создании упрочняющих покрытий на металлах и сплавах. Представлены результаты повышения физических, технологических и эксплуатационных характеристик покрытий, нанесенных методом ЭИЛ на титан и его сплавы [1; 2]; виден положительный эффект применения метода ЭИЛ на твердых сплавах [3; 4]. Кроме того, исследователи начинают проявлять интерес к ЭИЛ легких алюминиевых сплавов. Так, учеными [5] представлены характеристики микроструктуры и кавитационной эрозии покрытия из сплава Al-Si. Однако наиболее широкое распространение метод ЭИЛ получил при обработке поверхностей сталей [6–8]. В названных работах исследователи добились повышения термостойкости многослойного покрытия. Результаты зарубежных исследований свидетельствуют также об уменьшении коррозионной активности покрытия, полученного на нержавеющей стали методом электроискрового осаждения в расплавленном цинке [7].
В настоящее время проводятся исследования по разработке критериев эффективности [9; 10] и электрофизических моделей процесса ЭИЛ [11], которые позволяют найти зависимость критериев качества покрытия от технологических параметров процесса. Разработанные критерии метода ЭИЛ позволили выделить его в отдельный раздел материаловедения [12].
Однако практическое использование метода ЭИЛ (оптимизация параметров разряда и теплофизических свойств материалов, получение поверхностных слоев с заданной толщиной и функциональными свойствами) сдерживается отсутствием численных методов расчета температурного поля в процессе формирования покрытий на рабочих поверхностях обрабатываемого материала.
При выборе обрабатывающего материала для получения на обрабатываемом материале покрытий с заданными функциональными свойствами возникают сложности определения температурного поля в поверхностном слое при реализации метода1 [13–15].
В работах зарубежных [16-19] и отечественных исследователей [20; 21] рассмотрены некоторые математические модели определения температурного поля в поверхностном слое катода в процессе ЭИЛ. Однако описанные модели не учитывают ряд факторов и сложны в реализации.
Таким образом, целью данной статьи является получение полной математической модели определения темпера- турного поля при ЭИЛ в поверхностном слое обрабатываемого материала.
Материалы и методы
Рассмотрена задача нагрева катода, имеющего форму прямоугольного параллелепипеда ( Q 0 = {(‒ a , a ) × (‒ b , b ) × (0, c )}), в декартовой системе координат при ЭИЛ (рис. 1). Здесь P 0 = = { z = 0, x e ( - a , a ), y e ( - b , b ) } - рабочая поверхность; q 0 = q 0{ x , y , t } = q 0{ x' , t } – поверхностный тепловой поток; t – время; N – количество капель [20].
Капли Qi , равномерно заполняя некоторую часть грани { z = 0} (рис. 1), за один искровой разряд отдают посредством теплопроводности и излучения тепловой поток:
начально-краевой задачи нелинейной зависимости:
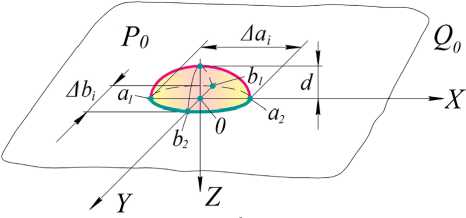
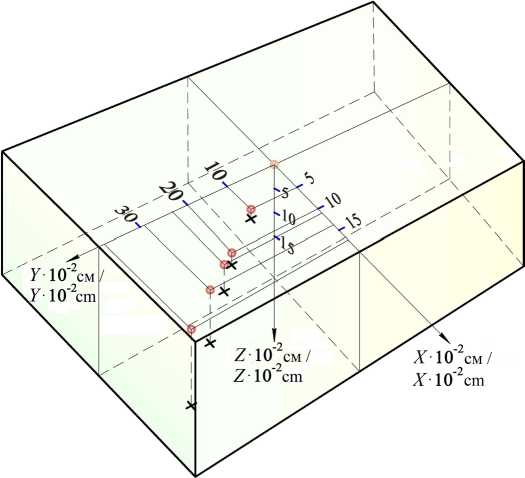
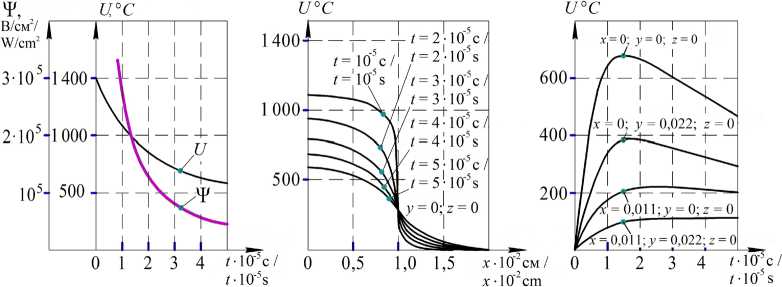
\лT-CpPpd 0=о,*eQo,tо d T гXk A T - ck P —i- = 0, x eQ, t0 < t < t *, i ∂tTo b=0=Фо(A * eQo, T^=0=Фi(x) , x e Qi, i = IN, (1) §1 - 0 T x-±a , dy * - 0 T 'y-± b , dzl = 0, qy= «i(T-Tr)+KoTi4, i=1,n, где αi – коэффициент теплоотдачи капель; Ti – температура i-ой капли; Tsr – температура окружающей среды; k = λ/(cρ) – коэффициент температуропроводности; σ – универсальная постоянная Стефана-Больцмана [Там же]. В математическом плане исследование теплового процесса (нагрева параллелепипеда и остывания капель Qi за некоторый фиксированный промежуток времени t* от начала воздействия искрового разряда t0) приводит к необходимости рассмотрения следующей ^ ^T0 + a, (T„ - Tsr) = 0, z = 0, 6 z N (x, y) ^UQ i, i=1 T = T, \ ^T^=к ^T, z = 0, p ∂z ∂z N (x, y) g|Jq i, i=1 ∂T Xk ^Ci + ak (T - TCP / sr ) + K°Ti = q0, dn P / -^ ed Qi, z < 0, Р и с. 1. Катод (прямоугольный параллелепипед Q0) с каплями на его поверхности P0; a, b, c – размеры катода в декартовой системе координат XYZ F i g. 1. The cathode (rectangular parallelepiped Q0 ) with drops on its surface P0; a, b, c – the size of the cathode in the Cartesian coordinate system XYZ . d2 d2 d2 где A = —v + —т + —т - оператор Лап-dx2 dy2 dzг ласа; T0 – температура катода; Tsr – температура окружающей среды; Φ0(x) Фi (A) - известные заданные функции; λp, λk, cp, ck, ρp, ρk, αp, αk – коэффициенты теплопроводности, удельной теплоемкости, удельной плотности и теплоотдачи параллелепипеда (p) и капель (k) соответственно; x = {x, y, z}, n - внешняя нормаль к ∂Ωi ; здесь и далее коэффициенты с индексом i = 0 относятся к катоду Q0, с индексами i Т 0 - к i-ой капле Qi; Qi = Qi Q{z = 0}, Qi = Qi|JdQi [Там же]. Ввиду сложности задачи (1) ее решение требует перехода к новым переменным: U = T0 ‒ Tsr; Ui = Ti ‒ Tsr; a2 = a0i = Xi J (ci pi). Тогда задача для параллелепипеда Q0 получит следующий вид: a0:АU = 0, х eQ , i = 0, N, 0 ∂t t0 < t < t *, N U\t.t,=Ф( x), x ■ Q, U |UQ. I V i=1 / U-.. - 0.U.. b - 0, ^-. - 0, (2> X, SU+apU = 0. z = 0, (x,y) e UПi. 8i=' Xk ^UX+“kUi+ K N z = 0, (x, y) g|Jq i, i=1 Фо(5c), 5c eQо где ф(5c) = < N фi (5c), z = 0, (5, y )e J Qi, i=1 ф0( DC) = Фо( x) - Tsr, Фi (X) = Ф i (X) - Tsr [Там же]. Предположим, что размеры капель малы; тогда температура внутри объема капли будет почти постоянна, а существенно изменяться она станет только во времени t. Будем считать, что при каждом t > 0 справедливы приближенные равенства, которые тем более верны, чем меньше размеры капли [Там же]: U (x, t) ©const,d U(X, t)/dt % const, x e Qi, i = 1, N, d U(5, t)/dz\z=-0 » const, x‘ePi, i = pj, (3) где Pi – основание i-ой капли. Это позволяет усреднить задачу по объемам Qi, ограничившись только областью Q0. Так как для нашего исследования важна не конкретная геометрическая форма капли, а лишь ее размеры, для простоты вычислений предположим, что капля заключена в параллелепипед определенного размера (рис. 2) [Там же]: Qi ={( axi, ai )x (bXi, b2i )x(0, d)}, A ai = a2 i-al i,A bi = b2 i - b, i; тогда ^| = Aai^bid, p = Дai^bi, S| = 2Aaid + +2A bd+A ai A bi. = 2d (A ai +A bi)+|P|. Результатом математических преобразований становится следующая задача для параллелепипеда Q0 [Там же]: a2A U- — = 0, xc e Qo, t0< t< t*, 0 d t 0 0 U\t=to = ф(5), DC e Qi, i = 0, N, 8U=±. - 0, Uy, - b=°. U=. - 0, (4> Р и с. 2. Расположение капли на катоде Q0 в декартовой системе координат XYZ F i g. 2. The location of a drop on the cathode Q0 in the Cartesian coordinate system XYZ — + h0U = 0, z = 0, (x,y) e HQi, 5 z м 8 U — + hU = qо 8 z — " 8U _ 1 cо 'U + cU + c2f (U) , о t N Z = 0, (x,y) e[jQi. i=1 Данная задача определена только в области Q0, так как граничное условие для температуры U заменяет все уравнения теплового баланса в каплях. Результаты исследования Для определения температуры катода в форме параллелепипеда Q0 решение задачи (4) состоит из двух этапов [Там же]. Первый этап Пусть U0 – решение задачи (5). С помощью найденного решения определим, что 0^(t) = qо - cо U + cxU0 + c2 f (U°) ; (x, y) eQi. (5) Второй этап Сложный нелинейный теплообмен между каплями Qi, i = 1, N и катодом Q0 в граничном условии задачи (4) заменяется линейным: d и N — + h0U = ^(t), (x,y)ellQi, t>0.5 z Для решения задачи применим вторую формулу Грина и функцию Грина G(:r, ^, t -т), которая является решением соответствующей задачи2 [20], где ^ = (^, П,z), t, т > 0. Тогда параллелепипед можно рассматривать как полупространство для капли, подставив в формулу (5) а = b = с = + ∞. Наиболее простым для численной реализации является случай полупространства {z > 0, x'^ R2} в качестве параллелепипеда Q0, на границу {z = 0} которого нанесена единственная капля {N = 1}, и значения коэффициента теплоотдачи αп = 0; следовательно, h0 = 0, то есть учитывается только теплообмен между каплей и катодом. Вторая формула Грина и данная функция Грина приводят задачу (4) к эквивалентному ей нелинейному интегральному уравнению следующего вида [20]: U ( jc, t) =U л( dc, t, t') - t a′b′ - a0 JdTJJG (5c,n,Z,0, t-t)Q (U )dndZ, (6) t' 0 0 где a' = ^a/2, b' = ^.b/2 - половинные длины сторон капли; ∞∞∞ Uл( X, t) =JJJ G (хД, t -1 ')U (£ t'd + 0 0 0 +a0 JdTJJG (x,^n,0, t -T q0&пД<М t' 0 0 dU (^,n,0,T) Q (U) = c0---------+ cU (^, П,0,т) + ∂τ + c2f (U (^,n,0,T)). Интегральные соотношения (6), как и задача (5), приближенно описывают процесс передачи тепла катоду каплей, помещенной на его границу. В подынтегральном выражении уравнения (6) функция U = U(ξ,η,0) рассматривается в области, в которой она почти постоянна по ξ,η. Поэтому, подставив в уравнение (6) z = 0 и проинтегрировав его [Там же], получим нелинейное интегральное уравнение типа Вольтера: A a AbU (t) = UЛ(t) - - a02 fG (t - TQ (U (t)W (7) Uл(x,y,z,t) =jjjjjq d^dndzdxdy, 0 0 0 0 0 T=0 x где Ф(x) = e dt - интеграл вероят- П0 ности3. Для численного решения задачи (6) введем пространственную и временную сетку (xi, y,, zk)), i = 1, N„ j = 1, N2, k = 1,N3, {0 = 10< t1<... < tNo = t*}. Тогда Uj = (xt, yj, zk, tn) - температура в узле (xi, yj, zk) в момент времени t = tn. Производную по времени заменяем разностным соотношени- ∂U U-U ем — = n^---n-1, где U = U ∂t ∆τn nt ∆τn=tn-tn-1. В уравнении (7) заменяем в подынтегральном выражении U(t) на Un+ Un-1 и получаем:2 — Gn c A a A bUn = UЛ n — . Un — Un—1 + , Un + U, '0 At + c12 относительно усредненной функции +С2 f lUn^— , ab U (t) = U (x, y ,0, t )dxdy. AaAb00 Здесь abab G (t - т) = jjjj G dxdyd^dn = 0 0 0 0 z=0 Z=0 + , X a Ф _ ( b ] a0 (t — t) bФ| . =l+ 0 L Ui( (t — t)) v n -( —T e T V r —_ e* a к a2 — a о (t—T) — )■ X bb — )_ )1 T tn где: Gn = j G(tn -T)dT. tn-1 Решение нелинейного уравнения (5) описывает температурное поле катода под основанием капли в момент t = tn. Поле внутри параллелепипеда определяется простой квадратурой (6), имеющей следующий вид [20]: U (x, y, z, tn) = U. (x, y, z, tn) - tn -a2J G(x,y,z,tn-TQn(Un)dT, (9) tn-1 где ∞∞∞ U. (x, y, z, tn) =JJJ GT=tn-1 UnЦ^Л,z )dzdndz + 000 t = ", exp tn + J G(x,y,z,tn-T)q0(т№,(10) ab G (x, У, Z, t - T = JJG^=0d^dn = 0 0 z2 --? Г Z X ZX -1 , 4"'t■'ф| ,X+a |-ф| ,X-a| X 4^a0(t-T) L (27ao(t-t)J ^Va0(t-t)JJ x f У+b ) y-b ) ф -Ф . (270077-7)J (2Vo(7-TJ, Qn (Un) = c0 Un-Un-1+C1 Un+U At 2 +c2 f (Un +Un-1) I 2 ) Для численных расчетов интеграл (10) заменим на тройную сумму следующего вида: следует уплотнить вблизи начала координат. С учетом вышеизложенного получаем окончательные выражения для определения температурного поля в узлах xi, yj, zk параллелепипеда [Там же]: tn Uj = Uj - a0Q„ J G(Xi, yj, Zk, tn - T)dT, tn-1 и ik=Y V У Gj^Ujk k + л n nil hi ki n-1 il = 1 hi =1 ki = tn +qо J Gn(xi,у, ,Zk,tn -tW (12) tn-1 После этого получим все данные для перехода к следующему временному отрезку [tn, tn + 1]. Отметим, что такая математическая модель не учитывает влияние остальных капель на искомый поток. Для учета подобного влияния необходимо рассмотреть систему нелинейных интегральных уравнений следующего вида: JJJgl„ и.,Zk,41 WndZ. Среднеарифметическое значение функции относительно восьми узлов параллелепипеда (xi ,, xi )x (yj 1, yj) x x(zk-1,z;), Uj =U(xi,У},Zk,tn), i = 1,Ni, j = 1 N k = 1, N, определяется по формуле: ', 3 A ai A bi Ui (t) = U^ i (t) - - a021 ^U^Git, (t - т )Q (Uj (U)W, (13) tn-1 j=' где a2 i b2 i a2 i b2 i Gj(t - T) =JJJJ G dxdyd^dn, al i bl i a1 i bl i z=0 Z =0 a1i,a2i,b1i,b2i – координаты i-ой капли; N = 4 (в данном случае). Дискретизация по времени t преобразует систему (13) в систему нелинейных алгебраических уравнений: ijk U n-1 = ri-1, j-1, k-1 i-1,-1, k i-1, j, k-1 n-1+Un-1 +Un-1 + + +un z^j,k+un -^k-1 +un -j-1^ + un -j1k-1+ un -j1k AatAbU = U,j -a02'NN^GQ(Uj). (14) .j=1 . (11) Так как решение Un-,(^,n,Z) является убывающим от нуля до бесконечности по переменным ξ,η,ζ, очевидно, что узловые точки {x, }^, {yj }^i, {Zk}^=1 При этом поле внутри параллелепипеда определяется так: U (x, y, z, t) = UЛ(x, y, z, t) - N tn a2 i b2 i - a2 2 Ш G\ Q (U) d^dndT. (15) i=' tn- J, ib i z=0 z=0 Таким образом, определив поток Q(U) из одной капли в параллелепипед, можем начать рассмотрение упорядоченного (периодического по переменным х, у) множества капель [Там же]. Однако решение системы нелинейных уравнений вида (14) с последующим определением поля в области Q по формуле вида (15) становится трудоемким. Поэтому для решения задачи нелинейный поток из капель в параллелепипед заменяется линейным, что является более предпочтительным [Там же]. По представленному алгоритму создан пакет программ и проведены численные расчеты определения температурного поля параллелепипеда4. С учетом функций в выражениях (7) и (9) для численного интегрирования применялись квадратурные формулы5 с весовой функцией 1/V/. Пробные вычисления по разработанному алгоритму показали эффективность выбранного метода. Расчеты проводились с учетом следующих данных [Там же]. 1. Размеры капли: Dai /2 = 10-2 см; Dbi /2 = 2• 10 2 см; d = 10-2 см. Здесь размеры капли приняты неодинаковыми в ее основании, что соответствует более общей задаче – обработке посредством ЭИЛ не плоской (Ла = ЛЬ), а криволинейной поверхности. 2. Теплофизические константы: Tcр = = 20 °C; To = 1 400 °С (начальная температура капли); q0 = 0. 3. Материал капли – вольфрам (W): λk = 1,73 Вт/cм ∙ °C; ρк = 19,25 г/cм3; ск = 0,15 Дж/г ∙ К; αк = 0,001 Вт / (см2∙ °С). 4. Материал катода – железо (Fe): λk = 0,733 Вт/cм ∙ °C; ρк = 7,87 г/cм3; ск = 0,46 Дж/г ∙ К; αк = 0,001 Вт/(см2∙ °С). 5. Узлы пространственной сетки, см: {х^} = 0; 0,005; 0,01; 0,011; 0,013; 0,017; {yf=1} = 0; 0,01; 0,02; 0,022; 0,026; 0,034; {zt1} = 0; 0,001; 0,003; 0,006; 0,01; 0,015. Динамика температурного поля некоторых точек поверхности представлена в таблице. В круглых скобках даны координаты точек, обозначенных на Т а б л и ц а T a b l e Динамика температурного поля точек на поверхности в зависимости от времени The dynamics of the temperature field of points on the surface depending on time Время / Time Координаты точек / The coordinates of the points (1,1) (2,1) (2,2) (3,1) (3,2) (3,3) (4,1) (4,2) (4,3) (4,4) t = 1 ∙ 10–5 c / t = 1 ∙ 10–5 s 1 078 1 043 1 042 541 540 270 294 293 147 65 t = 2 ∙ 10–5 с / t = 2 ∙ 10–5 s 904 835 790 467 439 228 323 299 156 96 t = 3 ∙ 10–5 c / t = 3 ∙ 10–5 s 775 712 660 419 386 209 310 281 155 105 t = 4 ∙ 10–5c / t = 4 ∙ 10–5 s 670 617 568 375 342 193 287 258 148 106 t = 5 ∙ 10–5 c / t = 5 ∙ 10–5 s 585 538 495 334 305 177 260 234 139 103 4 Программный комплекс для моделирования теплопереноса материала при электрофизическом воздействии : свидетельство о гос. регистрации прогр. для ЭВМ / Власенко В. Д., Колисова М. В. № 2017611479 ; заявл. 06.12.16 ; опубл. 03.02.17. URL: http://www1.fips.ru/fips_servl/fips_servlet?DB= EVM&rn=4256&DocNumber=2017611479&TypeFile=html 5Крылов В. И., Шульгина Л. Т. Справочная книга по численному интегрированию. М. : Наука, 1966. 372 с. рис. 3. Числа n и m в круглых скобках указывают на номер координаты вектора x = {xi} и вектора y = {yi} (например, точка (3, 1) таблицы соответствует точке (х3, у1) на плоскости x0y) [Там же]. Том 29, № 2. 2019 На рис. 4 представлена динамика температурного поля и вычисляемого потока в соответствии с формулой (5). Кривые на рис. 4, а иллюстрируют убывание температурного поля начала ко- Р и с. 3. Схема расположения точек, в которых вычислялась температура F i g. 3. The location of the points at which the temperature was calculated a) b) c) Р и с. 4. Динамика температурного поля и теплового потока: а) изменение температуры капли (линия U) и теплового потока (линия ψ) во времени; b) зависимость температуры поверхности октанта от координаты в сечении y = 0, z = 0; с) изменение температуры внутренних точек октанта, расположенных вне основания капли, во времени F i g. 4. The dynamics of the temperature field and heat flux: a) change in temperature of the droplet (line U) and heat flux (line ψ); b) the dependence of the octant surface temperature on the coordinate in the section y = 0, z = 0; c) the temporal variation of the temperature of the internal octant points located outside the base of the drop ординат (линия U) и потока (линия ψ). На рис. 4, b показана динамика температурного поля сечения y = 0, z = 0; на рис. 4, c - динамика точек, расположенных вне основания капли [Там же]. Обсуждение и заключение Анализ полученных результатов показывает, что поле в точках, расположенных в основании капли, постоянно убывает (рис. 4, а); в точках, расположенных вне основания капли (как на поверхности, так и в глубине катода), сначала возрастает, а затем убывает вместе с полем капли (рис. 4, с). Это свидетельствует о том, что, пока капля достаточно горячая, тепла к данным точкам прибывает больше, чем убывает, что и приводит к увеличению температуры. Однако по мере охлаждения капли приток тепла становится меньшим, чем отток, что приводит к уменьшению температуры [Там же]. Чем ближе расположена точка к поверхности капли, тем более резко возрастает температура в начальный момент времени и тем раньше она стабилизируется и начинает убывать. Температура в точках, расположенных симметрично относительно границы капли, симметрично изменяется относи- тельно температуры границы. Температура на границе капли примерно в два раза ниже температуры в центре капли. Предложенная модель реализована численно для случая одной капли, помещенной на границу теплопроводящего полупространства. Разработанный численный метод расчета позволяет приближенно описать процесс остывания одной капли и затем использовать полученную информацию для усредненного описания эффекта нагрева параллелепипеда группой капель [Там же]. Применительно к ЭИЛ построен алгоритм и проведены численные расчеты для определения значений температуры во всех точках, а также температурного потока в катоде (параллелепипеде) в случае одной среднестатистической капли на его грани. Сложный нелинейный теплообмен между каплей и катодом заменяется линейным теплообменом. Предложенный метод расчета для усредненного описания эффекта нагрева тела параллелепипеда рядом таких капель находит практическое применение в выборе материала анода в зависимости от эрозионной стойкости при получении покрытий с заданными функциональными свойствами. Поступила 11.02.2019; принята к публикации 22.04.2019; опубликована онлайн 28.06.2019 Об авторах: Все авторы прочитали и одобрили окончательный вариант рукописи.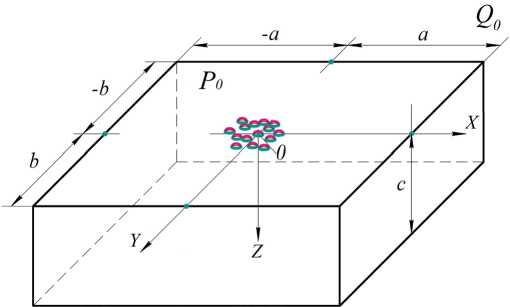
Список литературы Моделирование температурного поля поверхности при электроискровом легировании металлов
- Electrospark alloying of titanium and its alloys: the physical, technological, and practical aspects. Part I. The peculiarities of the mass transfer and the structural and phase transformations in the surface layers and their wear and heat resistance/V. V. Mikhailov //Surface Engineering and Applied Electrochemistry. 2013. Vol. 49, issue 5. P. 373-395. DOI: 10.3103/S1068375513050074
- Власенко В. Д., Мулин Ю. И. Формирование износо-и жаростойких покрытий на поверхностях титановых сплавов методом электроискрового легирования//Физика и химия обработки материалов. 2015. № 1. С. 79-84.
- The formation of protective coatings on tungsten-containing hard alloys by electrospark alloying with metals and borides/A. D. Verkhoturov //Inorganic Materials: Applied Research. 2011. Vol. 2, issue 2. P. 180-185. DOI: 10.1134/S2075113311020213
- Contribution of electrospark alloying to the oxidation resistance of hard tungsten alloys/A. D. Verkhoturov //Powder Metallurgy and Metal Ceramics. 2008. Vol. 47, no. 1-2. P. 112-115. DOI: 10.1007/s11106-008-0015-2
- Microstructure and cavitation erosion characteristics of Al-Si alloy coating prepared by electrospark deposition/W. Wang //Surface and Coatings Technology. 2008. Vol. 202, issue 21. P. 5116-5121. DOI: 10.1016/j.surfcoat.2008.05.013
- Исследование жаростойких свойств покрытий после электроискрового легирования стали 45 хромоникелевыми сплавами/A. В. Козырь //Письма о материалах. 2018. Т. 8, № 2. С. 140-145.
- DOI: 10.22226/2410-3535-2018-2-140-145
- Sun P.-F., Zhang L.-Q., Lin J.-P. Corrosion behaviour of Ti-45Al-8Nb coating on 304 stainless steel by electrospark deposition in molten zinc//Transactions of materials and heat treatment. 2014. Vol. 35, issue 2. Р. 151-156. URL: https://www.researchgate.net/publication/289541667_Corrosion_be-haviour_of_Ti-45Al-8Nb_coating_on_304_stainless_steel_by_electrospark_deposition_in_molten_zinc
- Fabrication of stainless steel microstructure surface by electro-spark deposition/W. Wang //Surface technology. 2017. Vol. 46, issue 5. P. 159-164.
- DOI: 10.16490/j.cnki.issn.1001-3660.2017.05.026
- Ivanov V. I., Verkhoturov A. D., Konevtsov L. A. The development of criteria for evaluating the effectiveness of the surface layer formation and its properties in the process of electrospark alloying. Part I. The state of the issue. Kinetic and functional criteria of the efficiency of a doped layer's formation//Surface Engineering and Applied Electrochemistry. 2017. Vol. 53, issue 3. P. 218-223.
- DOI: 10.3103/S1068375517030061
- Ivanov V. I., Verkhoturov A. D., Konevtsov L. A. The development of criteria for evaluating the effectiveness of the surface layer formation and its properties in the process of electrospark alloying (ESA). Part 2. The criteria of the effectiveness of the ESA process and electrospark coatings//Surface Engineering and Applied Electrochemistry. 2017. Vol. 53, issue 3. P. 224-228.
- DOI: 10.3103/S1068375517030073
- Electrophysical model of the erosion of electrodes under the energy pulse effect/P. S. Gordienko //Surface Engineering and Applied Electrochemistry. 2011. Vol. 47, issue 3. P. 206-216.
- DOI: 10.3103/S1068375511030045
- On the problem of creating a new scientific school in the field of electric erosion machining: Electrode material science/A. D. Verkhoturov //Surface Engineering and Applied Electrochemistry. 2010. Vol. 46, issue 5. P. 523-533.
- DOI: 10.3103/S1068375510050194
- Влияние природы электродных материалов на эрозию и свойства легированного слоя. Критерии оценки эффективности электроискрового легирования/А. Д. Верхотуров //Вестник Мордовского университета. 2018. Т. 28, № 3. С. 302-320.
- DOI: 10.15507/0236-2910.028.201803.302-320
- Смагин С. И., Власенко В. Д., Мулин Ю. И. Моделирование параметров процесса электроискрового легирования для образования функциональных поверхностей//Вычислительные технологии. 2009. Т. 14, № 3. С. 79-85. URL: http://www.ict.nsc.ru/jct/annotation/1303
- Верхотуров А. Д., Иванов В. И., Коневцов Л. А. Критерии оценки эффективности процесса электроискрового легирования//Труды ГОСНИТИ. 2011. Т. 107, № 2. С. 131-137.
- Xie Y.-J., Wang M.-C. Epitaxial MCrAlY coating on a Ni-base superalloy produced by electrospark deposition//Surface and Coatings Technology. 2006. Vol. 201, no. 6. P. 3564-3570.
- DOI: 10.1016/j.surfcoat.2006.08.107
- Electro-spark alloying using graphite electrode on titanium alloy surface for biomedical applications/T. Chang-bin //Applied Surface Science. 2011. Vol. 257, no. 15. P. 6364-6371.
- DOI: 10.1016/j.apsusc.2011.01.120
- Single-spark analysis of electro-discharge deposition process/B. Muralidharan //Materials and Manufacturing Processes. 2016. Vol. 31, issue 14. P. 1853-1864.
- DOI: 10.1080/10426914.2015.1127936
- Beck J. V. Transient temperatures in a semi-infinite cylinder heated by a disk heat source//International Journal of Heat and Mass Transfer. 1981. Vol. 24, issue 10. P. 1631-1640. (81)90071-5
- DOI: 10.1016/0017-9310
- Верхотуров А. Д., Козырь А. В., Коневцов Л. А. Научные основы разработки и получение слоистых материалов на поверхности твердых сплавов: монография. Владивосток: Дальнаука. 2016. 475 с. URL: http://www.im.khv.ru/metod/Science_basics_of_hard_materials.pdf
- Vlasenko V. D., Kolisova M. V. Modeling of the temperature field on the cathode's surface during electrophysical impact//Contemporary Engineering Sciences. 2016. Vol. 9, no 6. P. 249-256.
- DOI: 10.12988/ces.2016.611


