Моделирование температурного режима и прочности ледяного покрова

Цитирование: Васильев Е. Н. Моделирование температурного режима и прочности ледяного покрова / Е. Н. Васильев // Журн. Сиб. федер. ун-та. Техника и технологии, 2024, 17(7). С. 853–862. EDN: VUWXJE воды у нижней границы ледяного покрова, в котором появляются и смерзаются между собой кристаллы льда игольчатой формы (рис. 1 а), так и ближайший к границе раздела слой льда, где происходит структурная релаксация. В слое переохлажденной воды также могут зарождаться кристаллы внутриводного льда, которые всплывают к нижней поверхности льда, здесь происходят процессы их смерзания и дальнейшего замерзания находящейся между ними воды [1, 2]. Степень переохлаждения воды зависит от наличия механических примесей, имеющих высокую льдообразующую активность, и плотности теплового потока, обусловленного теплообменом водоема с окружающей средой. При таянии на нижней границе ледяного покрова может наблюдаться формирование острорельефной поверхности (рис. 1б). Таким образом, в процессах образования льда и его таяния на нижней поверхности ледяного покрова формируется переходный слой определенной толщины, включающий в себя среду как в жидком, так и твердом состояниях. Высота ледяного рельефа в таком слое может достигать нескольких сантиметров и зависит от величины тепловых потоков, обусловленных климатическими условиями, и иных факторов.

Таяние льда начинается на границах ледяных монокристаллов, из которых состоит по-ликристаллический лед, в результате между кристаллами образуется объемная сеть прослоек воды, вследствие этого в объеме льда появляется талая вода, имеющая положительную температуру [3]. Среда в таком промежуточном состоянии по своей сути является влажным льдом, оно возникает при таянии ледяного покрова в весенний период. На рис. 2а представлен слой льда с сформировавшейся вследствие внутреннего таяния столбчато-игольчатой структурой. При оттепелях ледяной покров может частично или полностью состоять из влажного льда, который имеет низкую прочность и легко разрушается на отдельные кристаллы при внешнем воздействии (рис. 2б). Для обеспечения безопасности хозяйственной деятельности, связанной с ледяными покровами, помимо контроля толщины льда необходимо диагностирование и прогнозирование перехода ледяного покрова в состояние влажного льда.

а                                               б

Рис. 1. Рост кристаллов на нижней границе льда осенне-зимнего образования (а) и вид нижней поверхности льда при таянии в весенний период (б)

Fig. 1. The growth of crystals on the lower boundary of the ice formed in autumn-winter (a) and the appearance of the lower surface of the ice during melting in the spring (б)

а

б

Рис. 2. Общий вид структуры тающего льда (а) и его разрушения на отдельные столбчатые кристаллы (б)

Fig. 2. General view of the structure of melting ice (a) and its destruction into separate columnar crystals (б)

Математическая модель динамики ледяного покрова

В холодный период года температурное состояние водоема определяется влиянием нескольких основных тепловых потоков. Тепловой поток qc , обусловленный конвективным теплообменом поверхности водоема (воды, льда или снега) с атмосферным воздухом, может иметь как положительное, так и отрицательное значение в зависимости от знака разности температур воздуха и поверхности водоема. На поверхность падает поток коротковолнового солнечного излучения, часть его отражается от поверхности, остальное излучение проникает в глубинные слои водоема и определяет мощность объемного тепловыделения qv при его поглощении в среде. Кроме того, с поверхности уходит собственное тепловое излучение водоема q_s , а поступает на поверхность длинноволновое излучение атмосферы qa . Испарение с поверхности водоема определяет тепловые потери q_e . Динамика фазовой границы «лед–вода» зависит от баланса тепловых потоков, подводимых к ней через слои льда и воды за счет теплопроводности.

Моделирование динамики ледяного покрова водоема проведено на основе численного решения задачи Стефана. Задача представлена в обобщенной формулировке, когда теплота фазового перехода q * «лед-вода» учитывается в величине эффективной теплоемкости среды [4]

ST

, . , .дТ d     ,dT

Cs^P^— = — ^(z) — at oz oz

dz

+ ч^) ,                               (1)

где cs , ρ – удельная эффективная теплоемкость и плотность среды; T – температура; λ – коэффициент теплопроводности; t – время; z – вертикальная координата, направленная вниз относительно поверхности водоема, qv – мощность объемного теплового источника, обусловленного поглощением солнечного излучения в глубине водоема. Неоднородность коэффициентов c_s , ρ и λ связана с наличием фазового перехода и различием теплофизических свойств сред (воды, льда и снега). На поверхности водоема задается граничное условие, которое учитывает теплообмен с окружающей средой для текущего состояния поверхности водоема (вода, лед или снег).

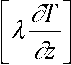
~ Чс + Ча ~ 4s ~ Че .                                            (2)

z=0

Соотношения для определения граничных тепловых потоков в формуле (2) приведены в [5]. На глубине водоема задается температура +4о С или значение, полученное в результате измерений.

В обобщенной формулировке задачи Стефана добавочная теплоемкость cf, обусловленная скрытой теплотой фазового перехода, задается в виде гладкой функции (рис. 3) в узком температурном интервале (Т*–ΔТ, Т*+ΔТ), удовлетворяющей условию нормировки г’+лг

\cf(T)dT = q*, т'-лт где Т* – температура фазового перехода, ΔТ – полуширина температурного интервала, в котором предполагается наличие переходной фазы среды, одновременно находящейся в твердом и жидком состояниях. Эта добавочная теплоемкость cf(Т) суммируется с обычной теплоёмкостью среды c(Т) и определяет ее эффективное значение cs(Т) = c(Т) + cf (Т). Причем в температурном интервале (Т*–ΔТ, Т*+ΔТ) изменение величин λ, ρ и c задавалось по линейному закону от значений для льда к значениям соответствующих воде.

Определение мощности объемного тепловыделения q_v было основано на решении уравнения Бугера-Ламберта, которое описывает поглощение излучения в полупрозрачной среде [6]

1^ = 1^е~к(:}: , где I(z), I(0) = (1–A)qr – интенсивность солнечного излучения в глубине слоя и на поверхности, k – эффективный коэффициент поглощения солнечной радиации, который определяет ослабление излучения в среде в условиях многократного рассеивания, A – коэффициент отражения

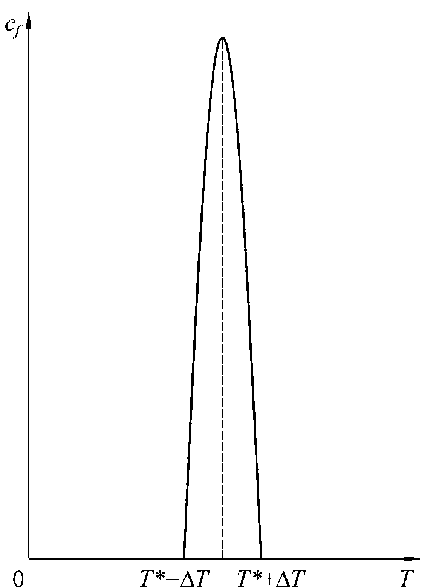
Рис. 3. Гладкая функция теплоемкости фазового перехода

Fig. 3. Smooth function of the heat capacity of the phase transition солнечного излучения поверхностью водоема. По распределению I(z) рассчитывается мощность объемного тепловыделения, используемая в уравнении (1), qv(z) = -dl(z)/dz.

Вычислительный алгоритм задачи (1)–(2) основан на неявной конечноразностной схеме [4]. В расчетах использовались следующие значения теплофизических параметров задачи: ρ = 1000 кг/м³, с = 4,2 кДж/(кг·К), λ = 0,6 Вт/(м·К), q ^* = 334 кДж/кг для воды; ρ = 920 кг/м³, с = 2,1 кДж/(кг·К), λ = 2,3 Вт/(м·К) для льда; ρ = 300 кг/м³, с = 2,1 кДж/(кг·К), λ = 0,275 Вт/(м·К) для снега. Значения оптических характеристик: для воды A = 0,08, k = 2 м^-1; для льда A = 0,3, k = 3,9 м^-1; для снега A = 0,8, k = 11,6 м^-1, эти характерные величины получены из экспериментальных данных [6].

Температурный режим и состояние ледяного покрова водоема

Моделирование температурного режима проведено для условий пресного озера (широта 56°04', долгота 92°44'), расположенного на окраине г. Красноярска, при этом использованы климатические данные в виде таблиц среднесуточных значений (температура воздуха, скорость ветра, влажность, поток солнечной радиации) холодного периода (октябрь 2022 – апрель 2023 гг.) метеостанции Минино, которая расположена вблизи этого озера. На рис. 4 приведены временные зависимости среднесуточной температуры атмосферного воздуха (сплошная линия).

Температурное состояние водоема в холодный период года зависит от климатических условий, наличия снега и его толщины, величины потока солнечного излучения, оптических и теплофизических свойств воды, льда и снега. С наступлением холодного периода с отрицательными температурами водная поверхность покрывается слоем льда, при выпадении осадков на нем появляется снежный покров. Наличие снега оказывает существенное влияние на тепловой баланс и температурный режим водоема вследствие изменения оптических характеристик

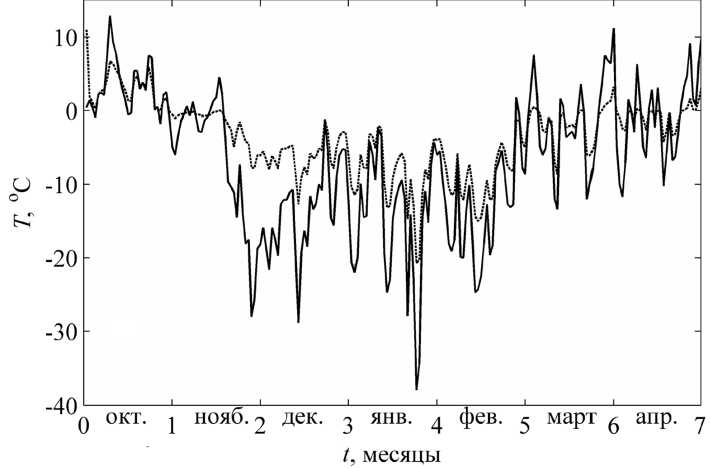
Рис. 4. Зависимости от времени температуры атмосферного воздуха (сплошная линия) и поверхности льда (пунктир) при толщине снежного покрова 5 см

Fig. 4. Time dependences of atmospheric air temperature (solid line) and ice surface (dotted line) with a snow cover thickness of 5 cm его поверхности и появления дополнительного термического сопротивления между воздухом и льдом. Рассчитанные значения температуры поверхности льда при толщине слоя снега 5 см (пунктир) существенно отличаются от температуры атмосферного воздуха (рис. 4).

Изменение состояния верхнего слоя водоема в холодный период года представлено на рис. 5. На рисунке приведены сплошными линиями изолинии, соответствующие значениям Т^* –Δ Т , Т^* , Т^* +Δ Т при Δ Т = 0,1^○С, также отображены области, которые отвечают различным температурным диапазонам и состояниям среды. Области 1 , 2 , 3 и 4 относятся к диапазонам Т >  Т^* +Δ Т , Т < Т^* –Δ Т , Т^* –Δ Т <  Т < Т^* и Т^* <  Т < Т^* + ΔТ соответственно. В начале рассматриваемого периода (октябрь) верхний слой водоема состоит полностью из слоя воды 1 . В течение холодного периода (ноябрь– февраль) идет практически монотонное нарастание толщины ледяного покрова 2 , при этом толщина слоя среды, соответствующей промежуточной фазе (области 3 и 4 ), мала. В марте и апреле периодически наступают оттепели. С наступлением оттепелей толщина слоя, соответствующая промежуточному состоянию «влажного льда», резко увеличивается, при этом зона 3 может достигать верхней границы ледяного покрова. Подтаивание и увлажнение льда вызвано изменением условий теплообмена с внешней средой, объемным тепловыделением, обусловленным поглощением солнечного излучения, и тепловым потоком со стороны дна. Для определения влияния величины Δ Т на результаты моделирования был проведен расчет при значении Δ Т = 0,2^○С, изолинии, соответствующие значениям Т^* –Δ Т , Т^* , Т^* +Δ Т , отображены пунктиром. Расположение сплошных и пунктирных изолиний для значения Т^* практически совпадает, наиболее заметное отличие в расположении сплошных и пунктирных изолиний наблюдается для значения Т^* +Δ Т. Таким образом, вычислительное моделирование позволяет определять и прогнозировать формирование внутри ледяного покрова слоев влажного льда, который имеет рыхлую, пропитанную водой структуру и характеризуется низкой прочностью даже при сохранении достаточной толщины.

Прочность ледяного покрова в значительной степени зависит от структуры и температуры льда. В экспериментальных исследованиях определена зависимость локальной прочности льда

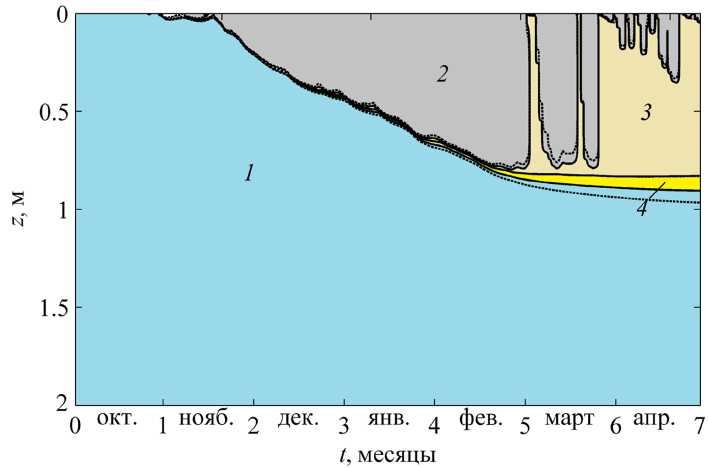
Рис. 5. Изменение состояния водоема в холодный период: вода ( 1 ), лед ( 2 ), влажный лед в температурных диапазонах 0^○С – ∆ T ( 3 ) и 0^○С + ∆ T ( 4 )

Fig. 5. Changes in the state of the reservoir during the cold period: water ( 1 ), ice ( 2 ), wet ice in the temperature ranges 0^○С – ∆ T ( 3 ) and 0^○С + ∆ T ( 4 )

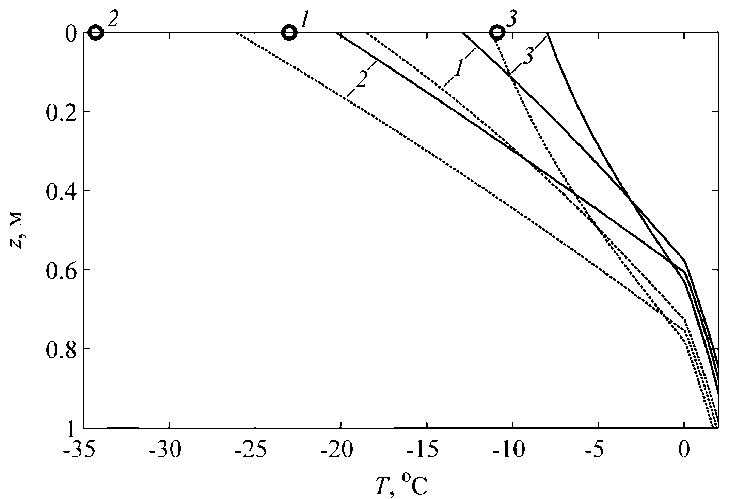
Рис. 6. Вертикальное распределение температуры в верхнем слое водоема

Fig. 6. Vertical temperature distribution in the upper layer of a reservoir от его температуры [7]. В реальном водоеме температура ледяного покрова имеет неоднородное распределение по вертикальной координате, зависящее в значительной мере от климатических условий и их временной динамики. На рис. 6 пунктирные линии описывают вертикальное температурное распределение T(z) в отсутствие снега, а сплошные линии – при высоте слоя снега 5 см, кружками отмечены среднесуточные значения температуры воздуха. Характерные точки излома температурных зависимостей соответствуют нижней границе ледяного покрова и воды. Особенно заметная перестройка температурного профиля происходит при резкой смене климатических условий. На рис. 6 приведены зависимости T(z), которые сформировались по истечении суток для календарных дат 20.01.23 (кривые и кружок 1), 22.01.23 (2) и 24.01.23 (3). В рассматриваемый период происходило резкое изменение температуры воздуха, а именно во временной промежуток с 19.01.23 по 24.01.23 были следующие среднесуточные значения –14,1○С, –23○С, –37,9○С, –34,3○С, –15,1○С и –10,9○С. При похолодании разница между температурами поверхности льда и воздуха увеличилась до 8–14○С, при дальнейшем потеплении эта разница снизилась до минимума. Такая запаздывающая температурная динамика объясняется большой теплоемкостью ледяного покрова.

Нагрузки и воздействия на гидротехнические сооружения зависят от прочности ледяного покрова, которая в значительной степени зависит от структуры и температуры льда. Предел прочности ледяного покрова на сжатие вычисляется как сумма пределов прочности заданного количества слоев льда, на которое разбивается рассматриваемый ледяной покров по вертикальной координате. Для этого по рассчитанному температурному распределению определяется локальная прочность слоев льда и далее проводится их суммирование [8]

^=,-^X(Q+M^{2 ,} V ^7V /=1

здесь C_i – значение прочности льда на одноосное сжатие (МПа) в i –ом слое при температуре T_i , ∆ _i – доверительная граница случайной погрешности определений C_i . На рис. 7 приведены временные зависимости интегральной прочности ледяного покрова R_c для температурных распределений T ( z ), которые сформировались в ледяном покрове при толщине снега 5 см (сплошная линия) и без снега (пунктир). В данном случае расчет прочности ледяного покрова проведен без учета случайной погрешности.

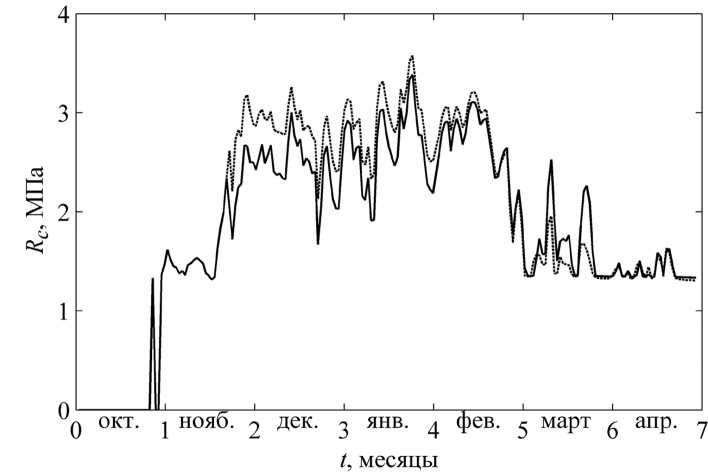
Рис. 7. Временная зависимость предела прочности ледяного покрова при сжатии

Fig. 7. Time dependence of the compressive strength of ice cover

Заключение

Таким образом, вычислительное моделирование позволяет оперативно получать информацию о динамике и состоянии ледяного покрова с учетом всего комплекса метеорологических факторов. Определение вертикального распределения температуры в ледяном покрове из натурных измерений требует значительных материальных и временных затрат. Метод вычислительного моделирования существенно менее трудоемок, при этом позволяет удаленно определять толщину, температурное состояние и прочность ледяного покрова. Результаты расчета толщины, температурного состояния и прочности ледяного покрова дают возможность оценивать безопасность функционирования хозяйственных объектов на текущий момент времени и предсказывать ее на будущий период на основе метеорологических прогнозов.