Моделирование температурных полей цистерны с бензином

На некоторых заправочных станциях цистерны с бензином находятся под открытым небом. Следовательно, они нагреваются солнечными лучами, а также происходит сезонное изменение температуры окружающей среды. Всё это приводит к изменению объема бензина в цистерне при том, что его масса сохраняется. Это необходимо учитывать при смешивании бензина, а также в процессе заправки транспортных средств. В связи с этим актуальным становится моделирование процесса нагревания бензина.

Составим математическую модель процесса нагревания. Поскольку цистерна с бензином является довольно сложным объектом, то процессы, происходящие в ней при нагревании, будем рассматривать отдельно для разных сред. Сначала опишем распространение тепла в стенках корпуса.

Схема цистерны с бензином приведена на рисунке 1.

Диаметр цистерны 20-25 метров, высота 10-12 метров.

Рассмотрим продольный разрез цистерны (рис. 2).

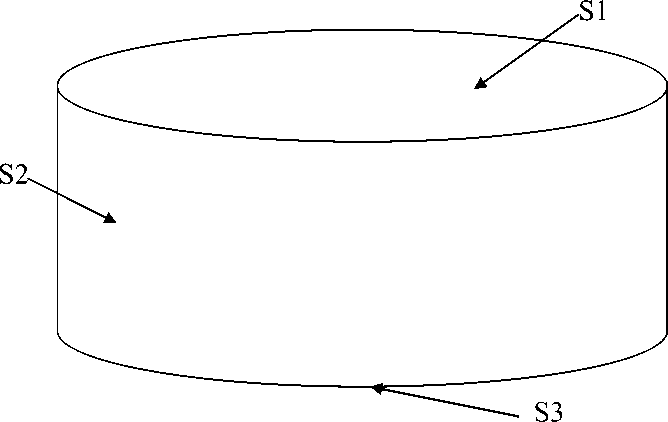
Рисунок 1 - Схема цистерны с бензином, установленной на АЗС

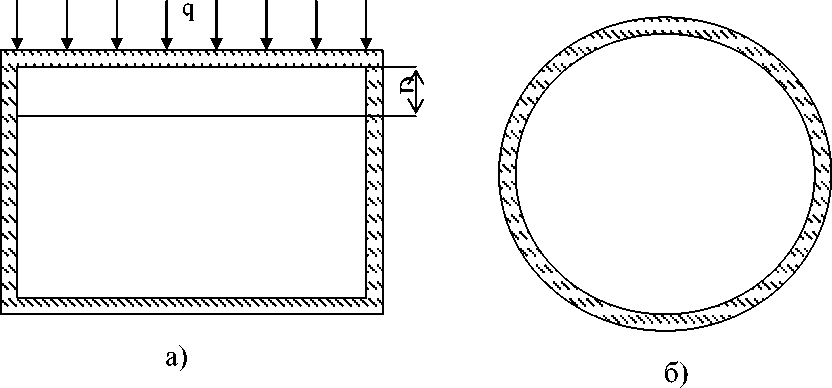
Рисунок 2. Разрез цистерны: а) вид сбоку; б) вид сверху без верхней стенки

Параметры объекта приведены в таблице 1.

Таблица1 - Параметры цистерны с бензином

Граничные условия Параметры объекта S1 S2 S3 R[м] H[м] S [м] q t1=20 t2=0 10 10 0,01 где q – тепловой поток; R – радиус цистерны; H – высота цистерны; S – толщина стенок.

Толщина листов стали, которые используются для внешней облицовки стенок корпуса (см. рисунок 2) составляет s 1 =0,01 м=10 мм.

Сверху на цистерну воздействуют солнечные лучи (тепловой поток q), сбоку температуру можно считать равной температуре окружающей среды, снизу температуру можно считать t2=0°С, т.к. это температура почвы.

Теплофизические свойства материалов, используемых в цистерне, приведены в таблице 2.

Таблица 2 - Теплофизические свойства материалов цистерны

Материал	X, Вт/(моС)	а, м2/с
Сталь	20,112	0,000019
Бензин	0,12	0,000092
Воздух	0,059	0,0000040

Математически перенос тепла внутри твёрдого тела описывается дифференциальным уравнением теплопроводности :

д Т

д ² Т   д ² Т   д ² Т

7 +   7 +   7

дх²   д у     дz²

где : Т (x , y, z, t) – температурное поле; t - время; a - коэффициент температуропроводности материала;

В цилиндрических координатах уравнение выглядит следующим образом:

дТ     д2 Т 1 д T д2 Тх

)   (1)

д r

— = a • (—г +--+ дт      дх2   R дr где: 0 < x < XL, 0 < r < R, a - коэффициент температуропроводности;

T(x,r,τ) – температурное поле цилиндра; τ – время.

Для получения математической модели объекта, соответствующей конкретной задаче, необходимо задание характеристик моделируемого объекта, граничных условий [2].

Рассмотрим процесс распространения тепла в стенках корпуса цистерны.

Поясняющий чертёж корпуса цистерны представлен на рисунке 3.

Перенос тепла в стальном корпусе (рисунок 3) описывается уравнениями:

д T       д 2 T   1 д T   д 2 Tx

1 = a1 • (+1 + дт       дx2   R  дr

0 < x < H, R - S < r < R, т > 0, дК     д2 T 1 dT

2 = a1 • (+   •   2 + дт       дx2 R д r д r2

H - s < x < H, 0 < r < R - S, T > 0, д T     д2 T 1 д T  д2 T4.

4 = a1 • (4- +4 + дт       дx2   R  дr   д r2

0 <  x <  S , 0 <  r <  R - S , т >  0 ,

a 1

коэффициент температуропроводности стали;  T1,  Т2,  Т4– температурное поле в стальных стенках цистерны; τ – время.

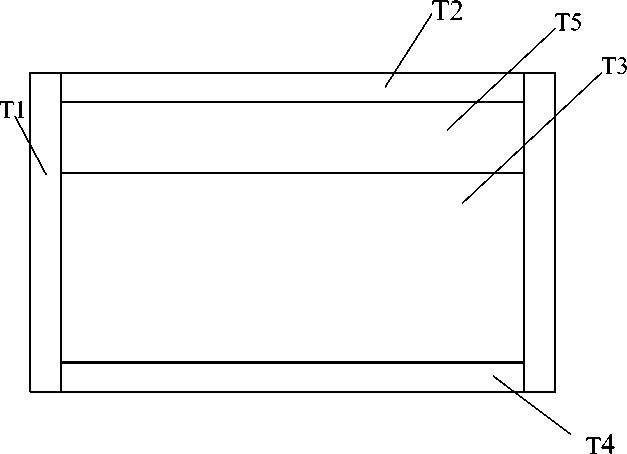
Рисунок 3 - Чертеж корпуса цистерны с обозначенными тепловыми полями

Перенос тепла в воздухе над поверхностью бензина описывается уравнением:

д Т д ² Т 1 д Т д ² Т_х —⁵ = a 2 • (— 5- + • —⁵ + —т⁵ ) дт д x ² R д r д r ²

H - 5 - D < x < H - S, 0 < r < R - S, T > 0, a2  –  коэффициент  температуропроводности воздуха; T5  – температурное поле в стальных стенках цилиндра; τ – время.

Перенос тепла в бензине описывается уравнением:

д T       д ² Т 1 д Т   д ² Т_3х

—³ = а ₃ • (— 3- +-- ³ + — з )

дт       д x ²    R д г    д r ²

S < x < H - S - D, 0 < r < R - S, T > 0,

a3–  коэффициент температуропроводности бензина;  T3  – температурное поле в стальных стенках цистерны; τ – время.

Положим, что в начальный момент времени температура во всех точках цистерны одинакова и равна температуре окружающей среды, т.е. 20

° С. Математически это условие выглядит следующим образом:

T ( x , r ,0) = 20, i = 1.. n , 0 <  x <  H , 0 <  r <  R.

Запишем граничные условия для системы уравнений (1 - 5).

Рассмотрим граничные условия между стенками цистерны и окружающей средой (см. рисунок 3). Положим, что температура наружных поверхностей корпуса постоянна. При моделировании на ЭВМ будем считать, что она равна 20 ° С. Граничные условия первого рода на наружных поверхностях корпуса выглядят следующим образом:

• а)    на границе дна корпуса и окружающей среды:

T ₄(0, r , т ) = 0,  0 <  r <  R , т >  0;                     (7)

• б)    на границе боковой стенки корпуса и окружающей среды:

T ( x , R,т ) = 20,  0 <  x <  H , т >  0;                 (8)

Передача тепла от воздуха к поверхности твёрдого тела происходит по закону теплопроводности, т.е. теплообмен соответствует граничным условиям четвёртого рода. Эти условия для границе стенок корпуса и воздуха внутри цистерны имеют вид:

• 1)    условия равенства температур:

T ₂ ( H - S , r , т ) = T ₅ ( H - S , r , т ), 0 <  r <  R - S , т >  0;

• 2)    условия равенства тепловых потоков:

„ dT 2 ( H - S , r , т )    , dT_s ( H - S , r , т )

^ '------dz-- ^Л 2------ gz ------.                     (10)

0 <  r <  R - S , т >  0;

где Х1 - коэффициент теплопроводности стали, Вт/(м2С);    Х2 - то же для воздуха.

Аналогично описываются граничные условия между стенкой и бензином в цистерне. Условия равенства температур имеют вид:

T ( x , R - S , т ) = T ₃ ( x , R - S , т ), S <  x <  S + D , т >  0;

условия равенства тепловых потоков:

„ дТ ( x , R - 5 , т )    , дТ ( x , R - 5 , т )

^Л------дZ------⁼ ''------dz ------•                      (12)

• 5 <  x <  5 + D , т >  0;

где Х ₃ - коэффициент теплопроводности бензина, Вт/(м²С).

Входное воздействие на объект управления имеет вид:

дТ2(H,r,т ) _

^Л      д^      q ^,                              (13)

0 <  r <  R , т >  0.

Таким образом, в данной статье была поставлена математическая модель распространения тепла в цистерне с бензином. На следующих этапах будет выполнена дискретизация модели и реализована компьютерная модель нагревания топлива в данной емкости на языке Python [1]. Это позволит учитывать температуру топлива при смешивании бензина, а также в процессе заправки транспортных средств.