Моделирование температурных полей в очаге деформации при прокатке сортовых профилей

Повышение качества металлоизделий является одним из основных направлений развития металлургической промышленности. Качество проката во многом определяет эффективность металлургических и металлопотребляющих предприятий.

В виду сложности процессов, происходящих при прокатке черных и цветных металлов, решены далеко не все вопросы, связанные с формированием качества металлопродукции, в частности, вопросы повышения качества за счет создания оптимальных технологий прокатки. Математические модели, описывающие процессы, протекающие в металле при его деформации и в технологическом потоке прокатного стана, могут служить базой для анализа и совершенствования существующих, и разработки новых технологий прокатки, которые обеспечивают получение качественного конечного продукта.

На кафедре ОМД ЮУрГУ были созданы ряд математических моделей процессов прокатки сортовых профилей, в частности:

• -    технологическая модель и, система анализа и проектирования режимов деформации;

• - математическая модель напряженно-деформированного состояния;

• -    математическая модель температурного поля в очаге деформации при прокатке сортовых профилей.

Технологическая модель расчёта режимов деформации создана на основе авторских и известных методик расчёта параметров процесса прокатки [1]. В модели использованы разработки кафедры ОМД ЮУрГУ, а так же разработки других авторских коллективов - УПИ, ДНИ, НИИМ и др. Математическая модель напряженно-деформированного состояния при прокатке сортовых профилей достаточно подробно изложена в работе [2].

Для моделирования температурных условий ведения процесса прокатки создана математическая модель температурного поля в очаге деформации. Задача решена методом конечных элементов на основе дифференциального уравнения теплопроводности [3].

С этой целью очаг деформации (% его часть) разбивается на 8 трехмерных комплекс-элемента с пятью узлами (рис. 1).

Для аппроксимации функции, описывающей распределение температуры внутри отдельного конечного элемента с номером (е) выбрана зависимость вида

Т^ = a^+a^z + a^x² ^y+c^z², которая обеспечивает существование всех частных производных уравнения теплопроводности.

В результате локальной аппроксимации для описания искомой функции Т = T(x,y,z) в пределах конечного элемента с произвольным номером (е) получим выражение

Т№ = N^T^ + N^T^ +N^T^ +

+N^T]W+N^T^\ где N*>e\x,y,z\..., N^\x,y,z) - функции формы конечного элемента (е); У\..., Т^ - узловые значения температуры.

Таким образом, в результате конечно-элементной аппроксимации температурное поле в очаге деформации при прокатке простых сортовых профилей описано с точностью до узловых значений температуры металла.

Для их определения использовалось дифференциальное уравнение теплопроводности [4], записанное в форме:

с • р • — = div^X • grad T) + rsH, 8t где с - удельная теплоемкость металла; р - массовая плотность металла; X - коэффициент теплопроводности; ts - сопротивление металла пластической деформации сдвига; Н - интенсивность скоростей деформаций сдвига.

Ввиду невозможности аналитического решения задачи для ее приближенного решения также использовалась разновидность проекционного метода - метод Галеркина.

При горячей прокатке теплообмен с окружающей средой в очаге деформации осуществляется в основном за счет контактного теплообмена с валками прокатного стана, теплопередачи излучением в окружающую среду и конвективной теплопередачи. Поскольку согласно известным ис- следованиям, конвективной теплопередачей можно пренебречь, для решения температурной задачи примем следующие граничные условия:

• 1.    На входе в очаг деформации температура металла считается известной.

• 2.    На свободной поверхности имеет место теплопередача излучением в окружающую среду, которая описывается формулой Стефана-Больцмана.

• 3.    На контактной поверхности имеет место теплообмен между деформируемым металлом и поверхностью валков, описываемый выражением

• 4.    На остальных поверхностях, ограничивающих % часть очага деформации, тепловой поток равен нулю.

где а, - коэффициент теплопередачи на контакт ной поверхности; Тв - температура валков.

Ряд преобразований позволяет свести задачу по определению узловых значений температуры к решению системы линейных уравнений.

kapTp=Ba

При этом коэффициенты системы линейных уравнений определяются по формулам

8     _ каР=^ J[c^ae)

е=1 j/GO

’ 3^  3N^  3^

v.——+Vv——+ v„ —

3x 3x 3y 3y 3z 3z

-as ^N^dS, где Ум - объем конечного элемента с номером (е); v - вектор скорости материальных частиц; S1^ - площадь поверхности конечного элемента.

Компоненты вектора свободных членов вычисляются по формулам

S =У f tsHN^dV + ОС             J J LA e-1 /(e)

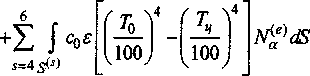
-asTb \N^dS, Sv где vx,vy,v2 - компоненты вектора скорости материальных частиц, определяемые в результате решения механической части краевой задачи.

Математическая модель позволяет выполнять численное моделирование температурного поля в очаге деформации и может служить частью комплекса для моделирования и проектирования технологии прокатки сортовых профилей.

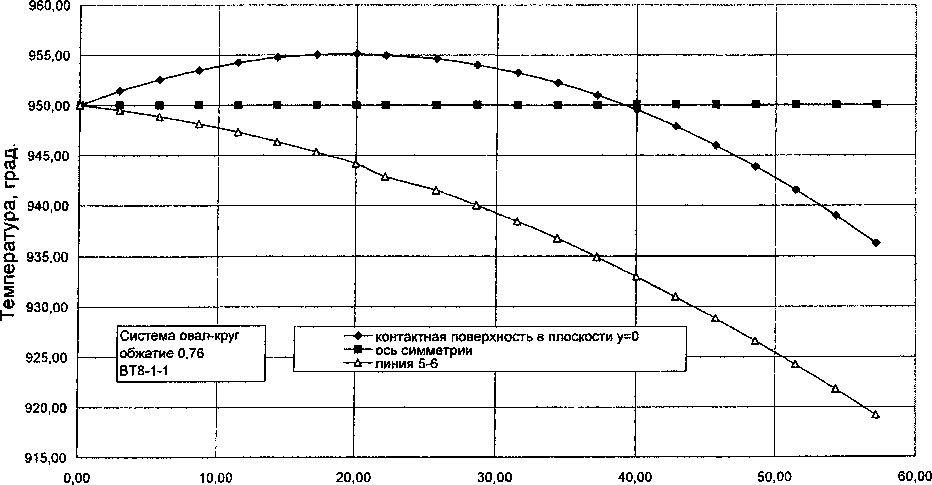
Моделирование температурных полей проведено для разных схем прокатки. На рис. 2 показаны результаты моделирования температурных полей в очаге деформации при прокатке в системе калибров овал-круг. Рассчитывалось изменение температуры металла вдоль очага деформации при движении вдоль продольной осевой линии, вдоль контактной поверхности по вершине калибра и вдоль свободной боковой поверхности (линия 5-6).

Анализ поля скоростей в этой схеме показал, что наибольшая интенсивность деформации наблюдается на контактной поверхности вблизи входа в очаг деформации, а наименьшая интенсивность деформации наблюдается на продольной оси симметрии вблизи плоскости входа, что и объяс-

Координата х, мм

Рис. 2. Распределение температуры вдоль очага деформации для системы овал - круг

няет в совокупности с условиями поверхностного теплообмена характер изменения температуры металла, приведенный на рис. 2.

При этом наибольшая потеря температуры наблюдалась в случае прокатки по схеме овал-квадрат, когда с геометрической точки зрения происходит наиболее резкий переход в месте сопряжения поверхностей профиля, наименьшая потеря температуры имеет место при прокатке по схеме круг-овал с достаточно гладкими переходами на поверхности профиля.

Характер изменения температуры металла существенно зависит от степени деформации. Так, с уменьшением степени деформации уменьшается деформационный разогрев на контактной поверхности, что приводит к большему падению температуры на контактной поверхности по сравнению со свободной боковой поверхностью, т.к. отвод тепла на контакте с валками более интенсивен по сравнению с теплопередачей излучением.

Увеличение степени деформации может привести к тому, что на контактной поверхности бу- дет происходить только разогрев металла.

При прокатке сортовых профилей из сплавов титана, соотношение между температурой на вы ходе и на входе в диапазоне температур нагрева 800...940 °C имеет практически линейный характер. Дальнейшее повышение температуры входа металла не дает существенного повышения температуры на выходе, так как в этом случае увеличивается разница между температурой металла и

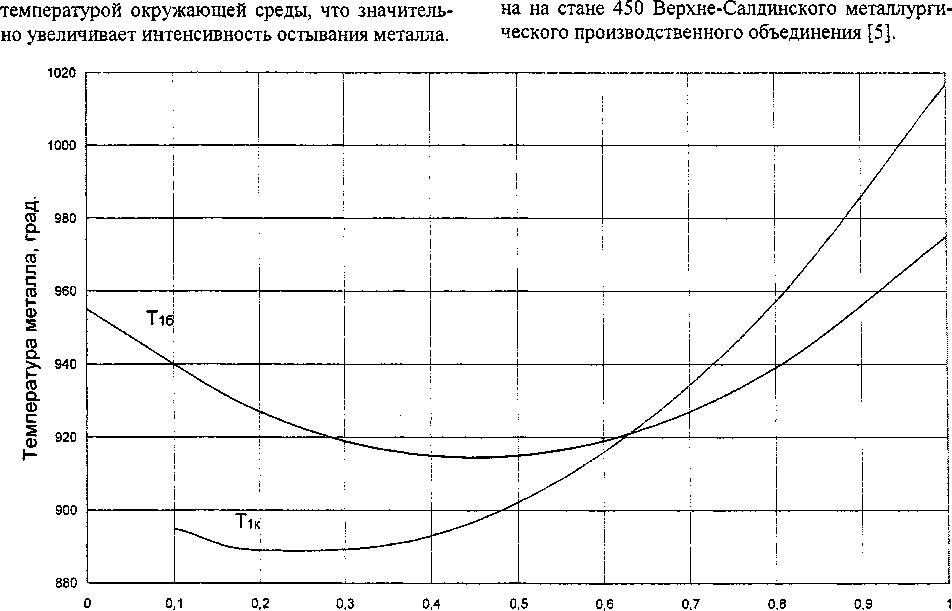
Результаты численного моделирования температурного поля показывают, что в зависимости от степени деформации при прокатке минимальная температура на выходе из очага деформации может быть как на контактной, так и на боковой поверхности профиля. В соответствии с этим построены графики (рис. 3) зависимости конечной температуры Т_1К металла, контактирующего с валком по вершине калибра, и конечной температуры Tib металла на свободной боковой поверхности от степени деформации Л при прокатке.

Как видно из рис. 3, до степени деформации Л « 0,64 на выходе из очага деформации минимальной является температура Tik, а при больших степенях деформации минимальной будет температура Т_]Б.

Создание моделей температурных полей и напряженно-деформированного состояния в очаге деформации позволила создать модель прогнозирования дефекгообразования при прокатке сортовых профилей и в результате численного моделирования проводить анализ различных технологических схем прокатки и проектировать новые технологии. Наибо лее актуальным это является для создания и усовершенствования прокатки профилей из труднодефор-мируемых и специальных сталей и сплавов, таких высокостоимостных, например, как сплавы титана.

Разработанные математические модели использовались при проектировании новых технологий и оборудования на ряде промышленных предприятий. На их основе была разработана технология прокатки сортовых профилей из сплавов тита-

Степень деформации

Рис. 3. Зависимость температуры от степени деформации

Выводы

• 1.    Создана математическая модель температурного поля в очаге деформации при прокатке сортовых профилей.

• 2.    Исследования, выполненные с использованием модели показали, что существенное влияние на характер изменения температурного поля вдоль очага деформации оказывает степень деформации.

• 3.    При прокатке титановых сплавов повышение температуры на входе выше 940 °C практически не влияет на температуру конца прокатки.

• 4.    Наибольшая потеря тепла имеет место при прокатке по схеме овал-квадрат, наименьшая - по схеме круг-овал.

• 5.    Созданные модели температурных полей и напряженно-деформированного состояния в очаге деформации позволяют создать модель прогнозирования дефектообразования при прокатке сортовых профилей

• 6.    Созданные модели могут применяться при проектировании новых и совершенствовании существующих технологий прокатки.