Моделирование теплопотерь нефтяных резервуаров методом наноразмерных клеточных автоматов

C urrently, steel cylindrical vertical tanks are widely used for the storage of oil and oil products. They are the most important and integral part of the country’s oil parks [1, 2]. High evaporation of petroleum and petroleum products leads to their significant storage losses [3, 4].

In the process of oil evaporation, a part of light hydrocarbons passes into a gaseous state, as a result of which a natural mass loss of the product occurs. The norms stipulate only a quantitative change, whereas during evaporation the qualitative composition of stored oil also changes. At natural pumping and handling temperatures during evaporation, light hydrocarbons of fraction 200 (up to and including hexanes), which are components of motor gasoline, are lost first of all. This reduces the quality of oil according to the «distillation» model, which takes into account the presence of light fractions in oil [5].

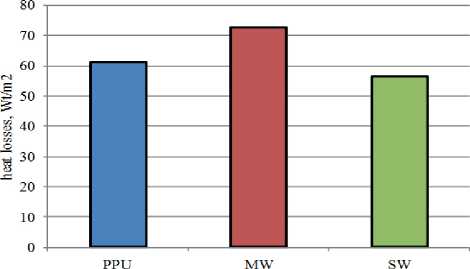
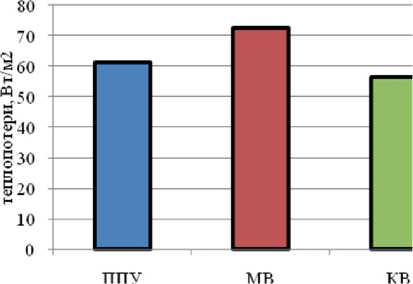
The intensity of oil evaporation, in addition to the technological regime with a change in the level of tank infusion [6], is determined by its temperature. In the conditions of the Russian north, when working with highly viscous oil, technological tanks of liquid and oil are equipped with thermal insulation [7]. Mineral wool (MW), polyurethane foam (PPU), stone wool (SW) are most widely used as a thermal insulation material. It should be noted that the heat-shielding properties of these materials at the initial stage of operation are at a comparable level (Fig. 1a). The practical choice is determined by other technological properties of thermal insulation – reliability, durability, flammability, etc. In par-ticular, the most common mineral wool has the worst thermal insulation properties of all materials

(Fig. 1a) and insufficient wear resistance due to increased crushability (Fig. 1b).

Polyurethane foam, despite its wide application at the facilities of the main oil transportation for engineering communications, has some flammability (group G2, G3 according to GOST 12.1.044-89 «Explosive and fire hazard of substances and materials») and therefore cannot be recommended without compromising the reliability and safety of reservoir hydrocarbon parks. The best thermal insulation for hazardous production facilities is stone wool (SW-thermal insulation).

MAIN PART

Development of one-dimensional model of thermal conductivity by the method of cellular automata (CAmodeling)

Practical management of the thermal regime of an oil reservoir is possible on the basis of modeling temperature conditions according to the results of monitoring the thermodynamic parameters of oil and the enclosing structures of the reservoirs. The article deals with the problem of modeling the temperature distribution in a cross-section of external fences of oil tanks. The solution is made on the basis of operational technological data of the reservoir parks of the northern fields of Russia. Calculations in the course of the development of temperature models were carried out for SW-thermal insulation.

The authors of [8, 9, 10, 11, 12] recommended the method of cellular automata to simulate thermal conductivity in the enclosing walls of technological facilities. In recent works [13, 14], using the CA-simulation, biological, physical, information processes are

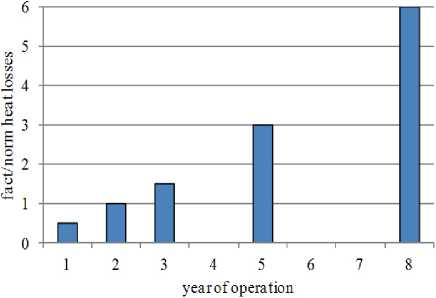
b aging intensity of MW-isolation

a - heat flux density

Fig. 1. Characteristics of oil tanks thermal insulation materials

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ simulated. This approach is especially productive when classical models are multifactorial differential structures [15].

The basis of the cellular automaton simulation is a discrete model — a regular grid of cells, for each of which a finite set of states is defined [16]. For each cell, a cell neighborhood is defined. At the same time, the initial states of all cells and the rules for their change are specified. Such method makes it possible to investigate the local mechanisms of the simulated system at the nanolevel [17].

The implementation of the CA-modeling was carried out for the tanks of the most common sizes – 5000 m3, 10000 m3 and 20000 m3. The ratio of tank wall thickness to diameter at a level of from 0,0005 m/m to 0,0009 m/m allows modeling in a one-dimensional format. To simulate the temperature behavior in a transverse section of external enclosures, nanoscale cells of a discrete temperature state were selected as local elements [18]. In this case, each cell is a trace element of the material – a «coarse-grained» substance.

According to the theory of finite state automation [19], the state of an individual cell at each time step changes in accordance to the transition function:

z(t _j ) = ϕ [z(t _j–1 ), X (t _j–1 )], (1)

where z(t _j ) – cell state at time t _j ;

X(t _j–1 ) – previous input vector.

Let’s consider a one-dimensional heat conduction problem, where a multi-layer outer barrier of an oil reservoir will act as an object, on the left border of which a thermal impulse is localized at the initial time [20]. We divide the enclosing surface into elements (cells) with the same step h and identify the state of the cell with its temperature T. The input signals simulate the process of transfer of thermal energy from neighboring cells and from the source of heat. For the case in question, the one-step transition function of the i-th cell is written as [21]:

T _i (t _j+1 ) = T _i (t _j )+(∆t/C•ρ)•[q _i-1 (t _j )+q _i+1 (t _j )+γ(t _j )], (2)

(T i–1 (t j )–T i (t j ) q _i–1 = λ       _h2

(T _i+1 (t _j )–T _i (t _j ) q _i+1 = λ       _{h 2}

where T _i (t _j ) – temperature of the i-th cell at time t _j ;

∆t – time step;

• C, λ and ρ – heat capacity, coefficient of thermal conductivity and density of the cell material, respectively;

q _i–1 (t _j ) и q _i+1 (t _j ) – specific heat flow rates from neighboring cells;

γ(t _j ) – power density of the heat source at the j-th moment of time.

The modeling process is reduced to determining the states of cellular automata at each step of discrete time [22]. In addition, each machine operates according to a specific algorithm. For internal cells of the reservoir wall, the transition function of the form (2)–(3) is used. For the external boundaries of thermal insulation, these dependences are modified on the basis of the hypothesis of a zero temperature gradient at these points (equality of heat fluxes from neighboring cells).

Under the conditions of practical implementation, one-dimensional modeling based on cellular automata is a sequence of iterative CA-interactions of the asynchronous type. Each iteration cycle involves the implementation of the following procedures:

• 1.    On the CA-field, a cell i = 1 is randomly identified with the x1 coordinate. All cells have equal probability of identification.

• 2.    The neighboring cell і = 2 with the x2 coordinate is randomly selected according to the neighborhood scheme from the Neumann neighborhood (the cell has only two neighbors, Fig. 2).

  

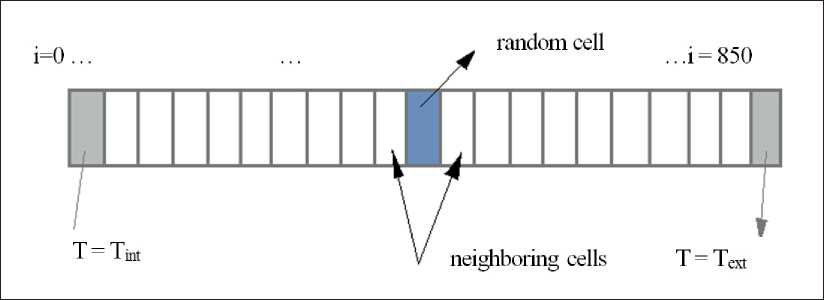
  Fig. 2. The cell structure of the enclosing wall of the tank

  
  

• 3.    Implemented CA-interaction between the selected cells. The meaning of interactions is to recalculate the temperature values of the insulating material of the reservoir in the cells of the simulation field according to equations (2)–(3), which are a cellular-automatic analogue of the thermal conductivity process [9].

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

In the simplest case of stationary heat conduction, the one-step transition function of the i-th cell is calculated by the formula:

Tij+1 = λiTij+ λi+1Tji+1/ λi+ λi+1, where j+1 – iteration number;

T^j _i+1 – new steady-state temperature in a random cell; T _i ^j – initial temperature in the same cell;

λ _i – coefficient of thermal conductivity of the material in this cell;

T^j _i+1 – temperature of one of the randomly selected neighboring cells;

λ _i+1 – coefficient of thermal conductivity of the material selected adjacent cells.

As applied to the particular case of modeling the temperature mode in the tank wall, the problem is formulated as follows. The oil tank is covered with thermal insulation made of basalt fiber mineral wool – stone wool (SW). From the inner side, a layer of paraffin deposits is formed on the tank walls. The main characteristics of the tank fences are shown in Table 1.

The results of the simulation of one-dimensional field of 850 cells, within the error of the cellular automaton «noise», are shown in Fig. 3.

CA-simulation optimization

Obviously, to ensure the adequacy of the simulation results to the actual process, the dimension of the model field should be taken as large as possible. However, this will inevitably increase the duration of modeling, even with the use of modern high-speed computing equipment [9, 11].

To assess the degree of influence of the number of CA on the result of temperature modeling, we constructed

Table 1

Technical characteristics of the external fences of the tank

№	Layer name	Thickness	Coefficient of thermal conductivity	Number of cells
		mm	Wt/(m2К)	pieces
1	Sediments	1	0,4	10
2	Steel sheet	24	52,0	240
3	Thermal SW insulation	60	0,032	600
	TOTAL	85		850

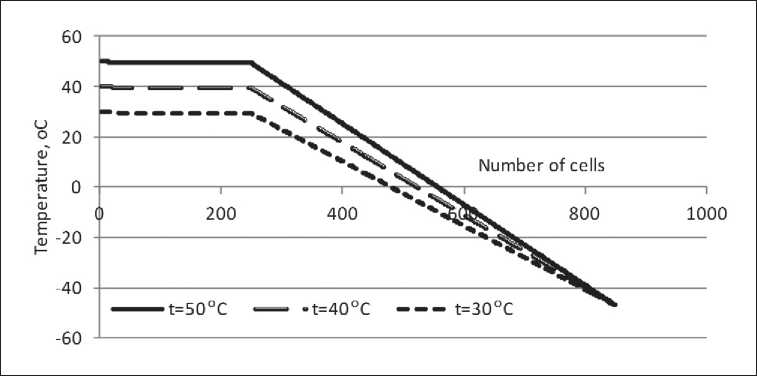
Fig. 3. Model temperature lines for three thermal modes of the tank: t_int = 30^oС, t_int = 40^oС, t_int = 50^oС

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ models for three cases of field dimensions. On the basis of previously conducted computational experiments, 17, 85, and 850 cellular automaton were selected by layer thickness. The layer of thermal insulation was taken as a layer, since in the metal wall of the tank, the temperature changes slightly and its dynamics are of no practical interest. The simulation results are shown in Fig. 4.

Absolute deviations of the model temperature from the calculated analytically are shown in Fig. 5.

The assessment of the quality of the constructed model was carried out by the magnitude of the standard deviation of the model temperature from the analytically calculated temperature (Fig. 6).

The simulation results showed that in the considered problem, the standard deviation σ is related to the dimension of the cellular automaton field N by the dependence of the form

σ = 28,75×N–0,386. (4)

The choice of the necessary and sufficient dimensionality of the cellular automaton field is the main step in the simulation. Assigning the field dimension at an optimal level minimizes time costs and at the same time provides the required accuracy of the results. From Fig. 6, it can be seen that as the CA-field dimension increases, the root-mean-square error in temperature modeling monotonously decreases. However, the concomitant increase of comparison pairs in the structure of a spacecraft leads to a significantly increased modeling time and, consequently, decreased efficiency of obtaining results. This is a significant drawback in the production monitoring of the field equipment operating mode.

The optimal solution should be made on the basis of the accuracy of the in-struments used to monitor the temperature of the medium in the tank and on the surface of the insulating layer. As a rule, chromel-copel (HC) thermocouples are used to measure temperatures in the range (–100; +100)oС. In this temperature range, the permissible absolute error of instrumental control is ±2,5oС.

Using equation (4), it was found that to ensure such accuracy, the dimension of the spacecraft with the number of simulation cells N = 560 is sufficient (Fig. 6).

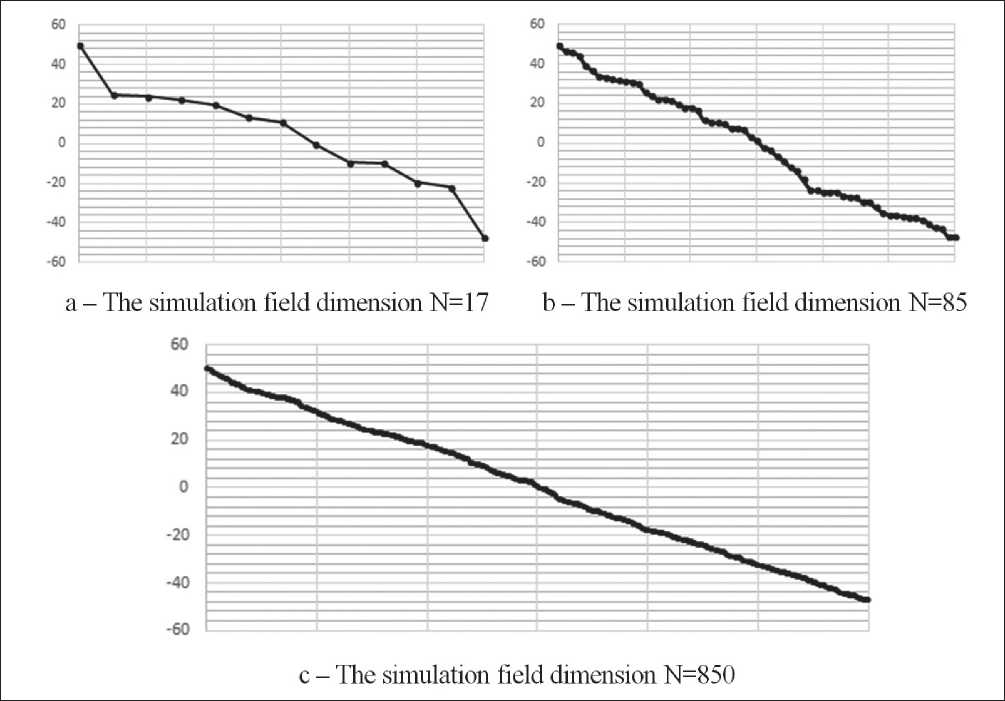
Fig. 4. Results of modeling the temperature distribution across the thickness of the thermal insulation of the tank depending on CA-dimension, ^oС

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

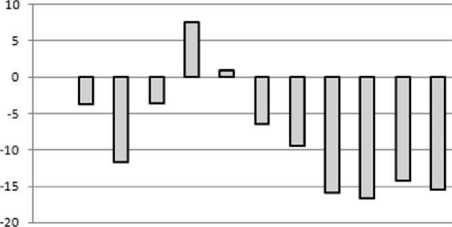
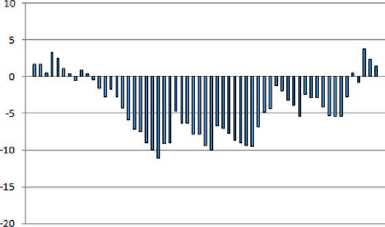
a - The simulation field dimension N=17

b - The simulation field dimension N=85

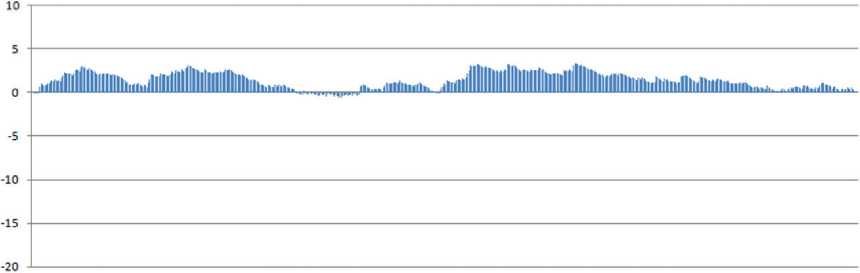
c - The simulation field dimension №850

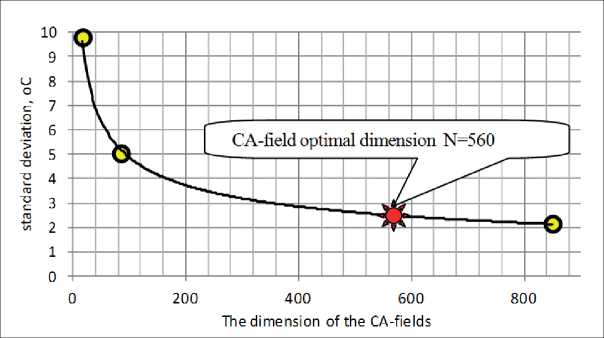
Fig. 5. Difference of model and analytically determined temperature through the thickness of the thermal insulation of the tank depending on the CA-dimension, ^oС

Fig. 6. Dependence of modeling accuracy on the CA-field dimension

CONCLUSION

• 1.    An alternative numerical method for solving heat conduction problems is considered. The temperature distribution in the outer insulating layer of the reservoir in the conditions of the Russia Extreme North f was obtained by the method of spacecraft modeling. It is shown that the standard deviation of the model 1,7^oС is provided by the dimension of the CA-field at the level of N = 850 cells.

• 2.    Conducting a virtual experiment on modeling thermal conductivity in an insulating layer made it possible

• 3.    It is shown that for the use of CA-modeling in industrial monitoring of operating modes of oil tank farms, the dimension of the CA-field N = 560 cells is optimal from the point of view of accuracy and efficiency of obtaining results.

to identify the power dependence of the mod-eling accuracy on the dimension of the CA-field for oil reservoirs in the parks of the central collection points of the northern oil fields. It is determined that the obtained dependence is characterized by the accuracy at the level of 0.99.

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

ВВЕДЕНИЕ

В настоящее время для хранения нефти и нефтепродуктов широко используются стальные цилиндрические вертикальные резервуары, которые являются важнейшей и неотъемлемой частью нефте-парков страны [1, 2]. Высокая испаряемость нефти и нефтепродуктов приводит к их значительным потерям при хранении [3, 4].

В процессе испарения нефти часть легких углеводородов переходит в газообразное состояние, в результате чего происходит естественная массовая убыль продукта. Нормами предусмотрено лишь количественное изменение, тогда как при испарении изменяется и качественный состав хранимой нефти. При естественных температурах перекачки и перевалки при испарении в первую очередь теряются легкие углеводороды фракции 200 (до гексанов включительно), являющиеся компонентами автомобильных бензинов. Это снижает качество нефти по «дистилляционной» модели, учитывающей наличие в нефти светлых фракций [5].

Интенсивность испарения нефти кроме технологического режима с изменением уровня взлива резервуара [6] определяется ее температурой. В условиях российского севера при работе с высоковязкой нефтью технологические резервуары жидкости и нефти оснащены тепловой изоляцией [7]. В качестве теплоизоляционного материала наиболее широко используются минеральная вата (МВ), пенополиуретан (ППУ), каменная вата (КВ). Следует отметить, что теплозащитные свойства названных материалов на первоначальном этапе эксплуатации находятся на сопоставимом уровне (рис. 1а). Практический выбор определяется прочими тех- нологическими свойствами тепловой изоляции – надежностью, долговечностью, горючестью и пр. В частности, наиболее распространенная минеральная вата обладает худшими из всех названных материалов теплозащитными свойствами (рис. 1а) и недостаточной износостойкостью из-за повышенной сминаемости (рис. 1б).

Пенополиуретан, несмотря на широкое применение на объектах магистрального транспорта нефти для инженерных коммуникаций, обладает некоторой горючестью (группа Г2, Г3 по ГОСТ 12.1.044-89 «Взрывопожароопасность веществ и материалов»), и потому не может быть рекомендован без ущерба надежности и безопасности резервуарных парков углеводородов. Оптимальной тепловой изоляцией для опасных производственных объектов является каменная вата (КВ-тепловая изоляция).

ОСНОВНАЯ ЧАСТЬ

Построение одномерной модели теплопроводности методом клеточных автоматов

Практическое управление тепловым режимом нефтяного резервуара возможно на основе моделирования температурных условий по результатам мониторинга термодинамических показателей нефти и ограждающих конструкций резервуаров. В статье рассмотрена задача моделирования распределения температур в поперечном срезе наружных ограждений нефтяных резервуаров. Решение выполнено на основе эксплуатационных технологических данных резервуарных парков северных месторождений России. Расчеты при разработке температурных моделей проведены для КВ-тепловой изоляции.

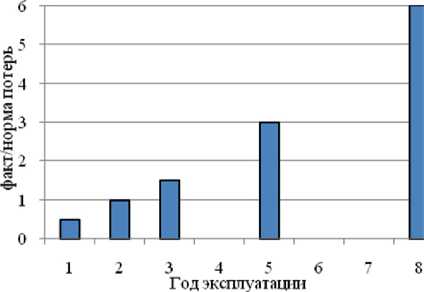
б - интенсивность старения МВ- изоляции

a - плотность теплового потока теплопотерь

Рис. 1. Характеристики материалов для тепловой изоляции резервуаров нефти

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

Авторами работ [8, 9, 10, 11, 12] для симуляции теплопроводности в ограждающих стенках технологических сооружений рекомендуется метод клеточного автомата. В последних работах [13, 14] с помощью КА-моделирования симулируются биологические, физические, информационные процессы. Такой подход особенно продуктивен в том случае, когда классические модели представляют собой многофакторные дифференциальные структуры [15].

Основой клеточно-автоматного моделирования служит дискретная модель – регулярная решетка ячеек, для каждой из которых определено конечное множество состояний [16]. Для каждой клетки определена клеточная окрестность. При этом задаются начальные состояния всех ячеек и правила их смены. Такой метод позволяет исследовать локальные механизмы моделируемой системы на наноуровне [17].

Реализация КА-моделирования проведена для резервуаров самых распространенных типоразмеров – 5000 м3, 10000 м3 и 20000 м3. Величина отношения толщины стенки резервуаров к диаметру на уровне от 0,0005 до 0,0009 м/м позволяет вести моделирование в формате плоской задачи. Для имитирования температурного поведения в поперечном срезе наружных ограждений в качестве локальных элементов были выделены наноразмерные ячейки дискретного температурного состояния [18]. В этом случае каждая ячейка-клетка представляет собой микроэлемент материала – «крупнозернистое» вещество.

Согласно теории конечных автоматов [19], состояние отдельной клетки на каждом шаге по времени изменяется в соответствии с функцией переходов:

z(t _j ) = ϕ [z(t _j–1 ), X (t _j–1 )], (1)

где z(t _j ) – состояние клетки в момент времени t _j ;

X(t _j–1 ) – вектор входных сигналов в предыдущий момент.

Рассмотрим одномерную задачу теплопроводности, где в качестве объекта будет выступать многослойное наружное ограждение нефтяного резервуара, на левой границе которого в начальный момент времени локализован тепловой импульс [20]. Разобьем ограждающую поверхность на элементы (клетки) с одинаковым шагом h и отождествим состояние клетки с ее температурой Т. Входные сигналы моделируют процесс передачи тепловой энергии от соседних клеток и от источника теплоты. Для рассматриваемого случая одношаговая функция переходов i-й клетки запишется так [21]:

T _i (t _j+1 ) = T _i (t _j )+(∆t/C•ρ)•[q _i-1 (t _j )+q _i+1 (t _j )+γ(t _j )], (2)

(T i–1 (t j )–T i (t j ) q _i–1 = λ       _h2

(T _i+1 (t _j )–T _i (t _j ) q _i+1 = λ       _{h 2}

где T _i (t _j ) – температура i-й клетки в момент времени t;

j

∆t – шаг по времени;

C, λ и ρ – теплоемкость, коэффициент теплопроводности и плотность материала клетки, соответственно;

q _i–1 (t _j ) и q _i +1(t _j ) – удельные мощности тепловых потоков от соседних клеток;

γ(t _j ) – удельная мощность источника теплоты в j-й момент времени.

Процесс моделирования сводится к определению состояний клеточных автоматов на каждом шаге дискретного времени [22]. При этом каждый автомат функционирует по определенному алгоритму. Для внутренних клеток стенки резервуара используется функция переходов вида (2)–(3). Для внешних границ тепловой изоляции данные зависимости

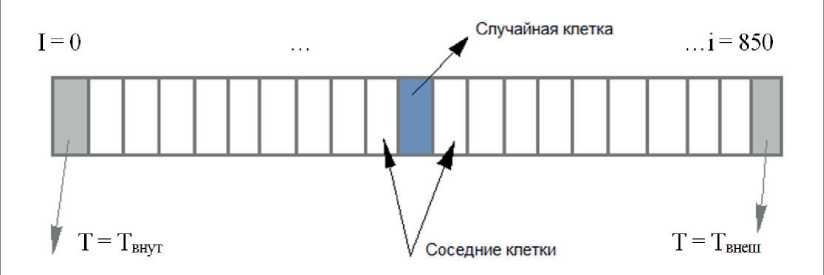
Рис. 2. Клеточная структура ограждающей стенки резервуара

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ модифицированы, исходя из гипотезы о нулевом градиенте температуры в данных точках (равенство тепловых потоков от соседних клеток).

В условиях практической реализации одномерное моделирование на основе клеточных автоматов представляет собой последовательность итерационных клеточно-автоматных взаимодействий асинхронного типа. Каждый итерационный цикл предусматривает реализацию следующих процедур:

• 1.    На КА-поле случайным образом идентифицируется некоторая клетка і = 1 с координатой x1. Все ячейки имеют одинаковую вероятность идентификации.

• 2.    Соседняя клетка і = 2 с координатой x2 выбирается случайным образом по схеме соседства из окрестности Неймана (у клетки есть только два соседа, рис. 2).

• 3.    Реализуется КА-взаимодействие между выбранными клетками. Смысл взаимодействий заключается в пересчете значений температуры теплоизоляционного материала резервуара в клетках поля моделирования по уравнениям (2)–(3), которые представляют собой клеточно-автоматный аналог процесса теплопроводности [9].

В простейшем случае стационарной теплопроводности одношаговая функция переходов i-й клетки рассчитывается по формуле:

Tij+1 = λiTij+ λi+1Tji+1/ λi+ λi+1, где j+1 – номер итерации;

T _i ^j+1 – новая установившаяся температура в случайной клетке;

T _i ^j – первоначальное значение температуры в этой же клетке;

• λ _i – коэффициент теплопроводности материала в данной клетке;

T^j _i+1 – температура одной из случайно выбранных соседних ячеек;

• λ _i+1 – коэффициент теплопроводности материала выбранной соседней ячейки.

В применении к частному случаю моделирования температурного графика в стенке резервуара задача формулируется так. Нефтяной резервуар покрыт тепловой изоляцией из минеральной ваты базальтового волокна – каменной ваты. С внутренней стороны на стенках резервуара образован слой парафинистых отложений. Основные характеристики ограждений резервуара приведены в табл. 1.

Результаты моделирования одномерного поля, содержащего 850 ячеек, в пределах погрешности клеточно-автоматного «шума» приведены на рис. 3.

Оптимизация клеточно-автоматного моделирования

Очевидно, что для обеспечения адекватности результатов моделирования реальному процессу размерность модельного поля следует принимать, возможно, большей. Однако это неизбежно увеличит продолжительность моделирования даже при использовании современного быстродействующего вычислительного оборудования [9, 11].

Для оценки степени влияния количества клеток автомата на результат моделирования температуры были выполнены построения модели для трех случаев размерности поля. На основе предварительно проведенных вычислительных экспериментов было отобрано 17, 85 и 850 клеточных автоматов по толщине слоя. В качестве слоя был взят слой именно тепловой изоляции, т.к. в металлической стенке резервуара температура изменяется незначительно и ее динамика не представляет практического интереса. Результаты моделирования показаны на рис. 4.

Абсолютные отклонения модельной температуры от вычисленной аналитически приведены на рис. 5.

Оценка качества построенной модели была проведена по величине среднеквадратического отклонения модельной температуры от аналитически рассчитанной (рис. 6).

Таблица 1

Технические характеристики наружных ограждений резервуара

№	Наименование слоя	Толщина	Коэффициент теплопроводности	Количество ячеек
		мм	Вт/(м2К)	шт
1	Отложения	1	0,4	10
2	Стальной лист	24	52,0	240
3	Тепловая КВ-изоляция	60	0,032	600
	ВСЕГО	85		850

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

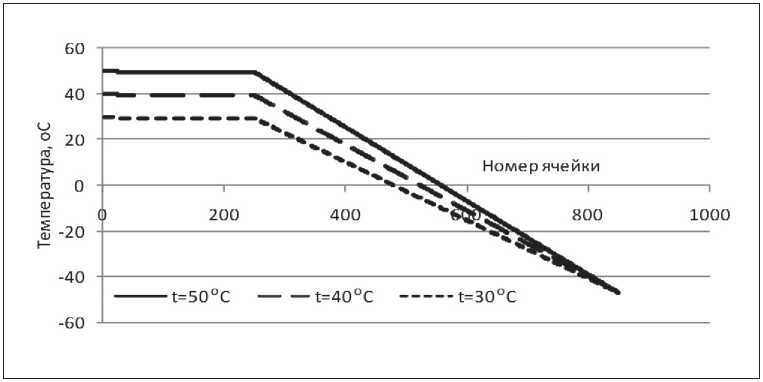
Рис. 3. Модельные температурные линии для трех тепловых режимов резервуара: t_вн = 30^оС, t_вн = 40^оС, t_вн = 50^оС

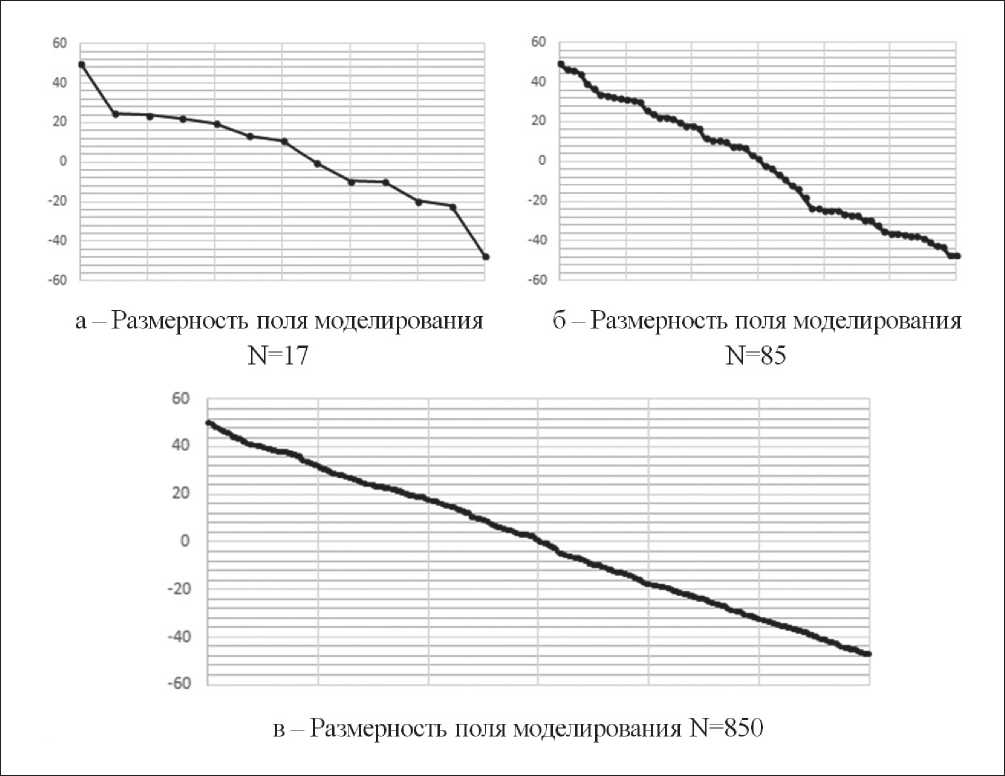
Рис. 4. Результаты моделирования распределения температур по толщине тепловой изоляции резервуара в зависимости от количества КА, ^оС

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

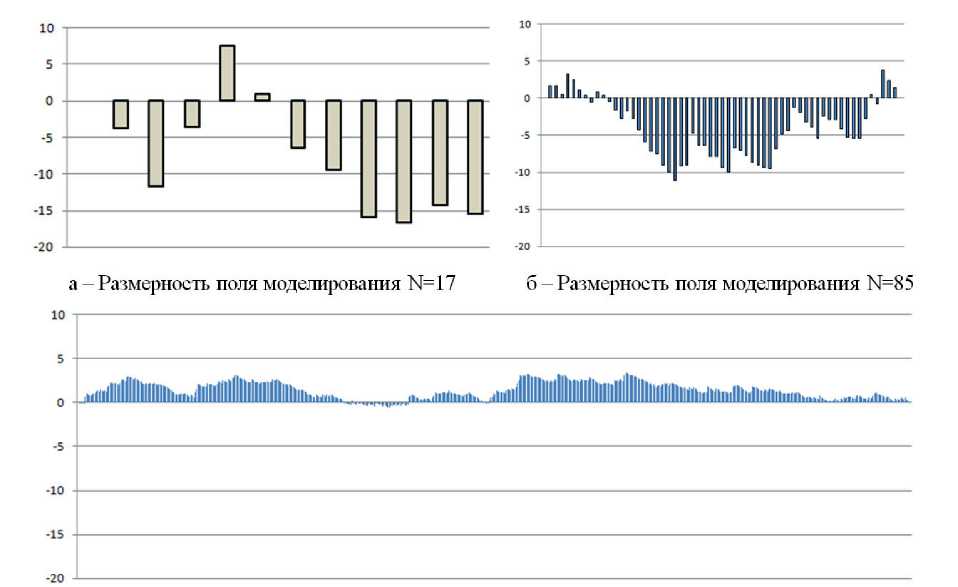
в - Размерность поля моделирования N=850

Рис. 5. Разница модельной и аналитически определенной температуры по толщине тепловой изоляции резервуара в зависимости от количества КА, ^оС

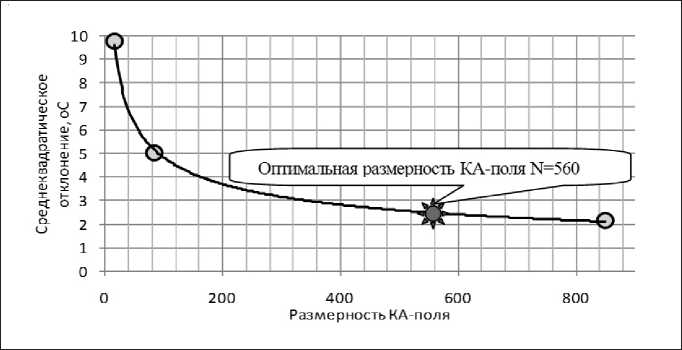
Рис. 6. Зависимость точности моделирования от размерности КА-поля

Результаты моделирования показали, что в рассматриваемой задаче среднеквадратическое отклонение σ связано с размерностью клеточно-автоматного поля N степенной зависимости вида

σ = 28,75×N–0,386. (4)

Выбор необходимой и достаточной размерности поля клеточных автоматов является основным этапом при моделировании. Назначение размерности поля на оптимальном уровне позволяет минимизировать временные затраты с одновременным достижением требуемой точности результатов.

NANOTECHNOLOGIES IN POWER ENGINEERING • НАНОТЕХНОЛОГИИ В ЭНЕРГЕТИКЕ

Из рис. 6 видно, что при увеличении размерности КА-поля среднеквадратическая ошибка моделирования температур монотонно снижается. Однако сопутствующее наращивание количества пар сравнения в структуре КА приводит к значительному увеличению времени моделирования и, как следствие, снижению оперативности получения результатов. Это является существенным недостатком в условиях производственного мониторинга режима эксплуатации промыслового оборудования.

Оптимальное решение следует принимать с учетом точности используемых приборов для контроля температур среды в резервуаре и на поверхности изоляционного слоя. Как правило, для измерения температур в диапазоне (–100; +100)oС используются хромель-копелевые (ХК) термопары. В этом интервале температур допустимая абсолютная погрешность инструментального контроля составляет ±2,5oС.

С помощью уравнения (4) было установлено, что для обеспечения такой точности достаточной является размерность КА-поля с количеством ячеек моделирования N = 560 (рис. 6).

ЗАКЛЮЧЕНИЕ

• 1.    Рассмотрен альтернативный численный метод решения задач теплопроводности. Получено распределение температур в наружном изоляционном слое резервуара в условиях Крайнего севера России методом КА-моделирования. Показано, что среднеквадратическое отклонение модели 1,7^oС обеспечивается размерностью КА-поля на уровне N = 850 ячеек.

• 2.    Проведение виртуального эксперимента по моделированию теплопроводности в изоляционном слое позволило идентифицировать степенную зависимость точности моделирования от размерности КА-поля для нефтяных резервуаров парков центральных пунктов сбора северных месторождений. Установлено, что полученная зависимость характеризуется дисперсией адекватности на уровне 0,99.

• 3.    Показано, что для КА-моделирования при производственном мониторинге режимов эксплуатации резервуарных парков нефти оптимальным с точки зрения точности и оперативности получения результатов является размерность КА-поля N = 560 ячеек.