Моделирование тепловых процессов при электронно-лучевой сварке разнородных материалов
Автор: Пермяков Глеб Львович, Ольшанская Татьяна Васильевна, Беленький Владимир Яковлевич, Трушников Дмитрий Николаевич
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Статья в выпуске: 6-2 т.15, 2013 года.
Бесплатный доступ
Разработана математическая модель электронно-лучевой сварки разнородных материалов на базе уравнения переноса энергии со смешанными граничными условиями и двумя наборами теплофизических характеристик, зависящими от координат. Решение краевой задачи получено методом функций Грина с использованием программы MathCad 15.
Математическая модель, электронно-лучевая сварка, разнородные материалы
Короткий адрес: https://sciup.org/148202570
IDR: 148202570 | УДК: 621.791.722
Текст научной статьи Моделирование тепловых процессов при электронно-лучевой сварке разнородных материалов
Дифференциальное уравнение переноса энергии является математической моделью целого класса явлений теплопроводности [1,2]:
- на поверхностях z=0 и z=5 раничные условия второго рода равны 0:
д T (д 2 T д 2 T д 2 T ) д T q — = a • -— + —- + —- + V — + — д t (д x 2 д у 2 д z 2 ) д x с р
д T д z
z = 0
д T д z
z =8
= 0
Оно имеет бесконечное множество решений. Чтобы получить из этого множества одно частное решение, характеризующее конкретный процесс, необходимо иметь дополнительные данные, не содержащиеся в исходном дифференциальном уравнении. Эти дополнительные условия, которые в совокупности с дифференциальным уравнением определяют конкретную задачу, называются условиями однозначности :
-
1) Расчётная схема - бесконечная пластина толщиной 5 :
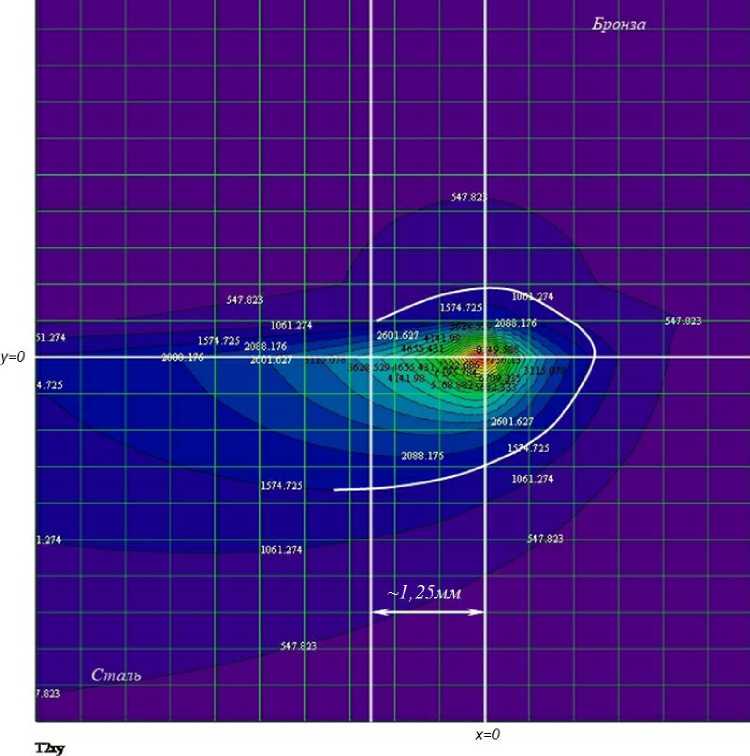
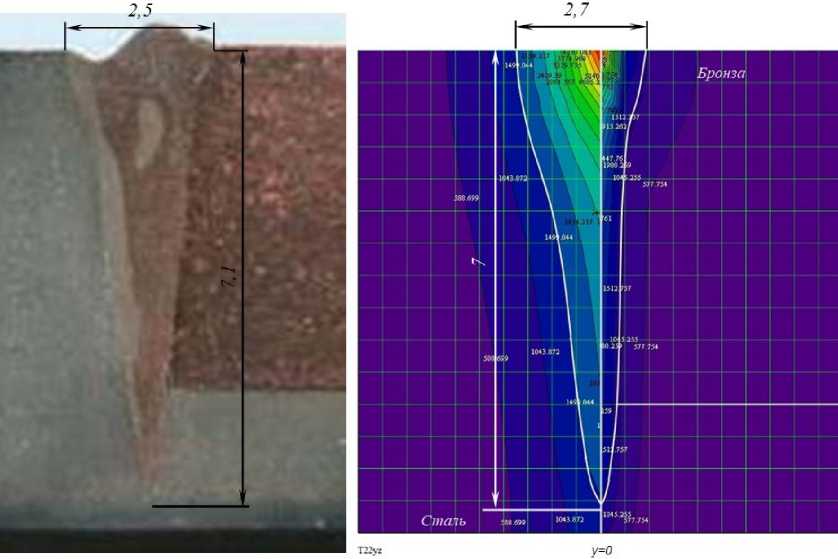
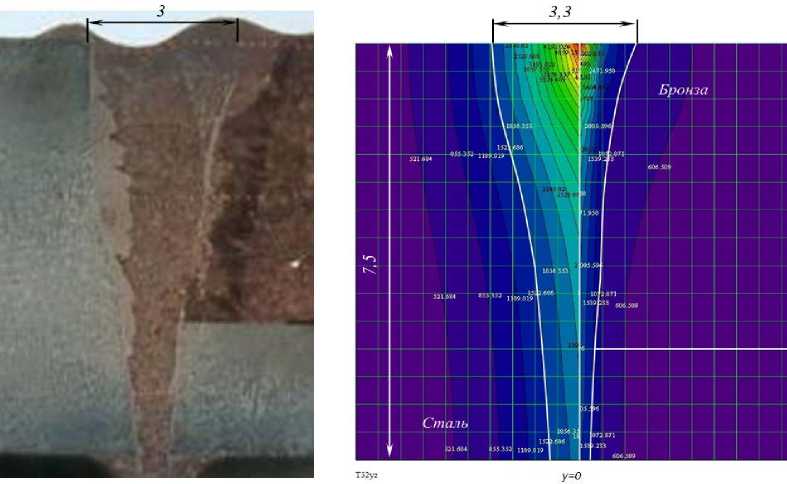
—ю 2) Граничные условия смешанного типа: - по x и у граничные условия первого рода равны 0; 3) Два набора теплофизических характеристик: с1, Х1, р1, а1 и с2, Х2, р2, а2; 4) Температура в начальный момент времени равна 0. Сварка производится по стыку двух материалов (вдоль оси x, у=0, z=0) со скоростью V, электронный луч мощностью q=I·U, диаметром d. Время сварки t. Решение краевой задачи производилось методом функций Грина. Интегральное решение уравнения переноса энергии имеет вид: T (х, у, z ,т) = JjJJ G (х,х', у, у', z, zт) • F (x, у, z, т )дx 'ду 'дz ‘дт т z у x где G(х,х',у,у',z,z'„т) - функция Грина, F(x,у,z,т) - функция источника. Известно, что функция Грина допускает неполное разделение переменных (она разделяется по пространственным переменным x,у,z, но не разделяется по времени т), т.е. может быть представлена в виде произведения: G (x, x', y, y', z, z \т ) = Gx (x, x \т ) Gy (y, y', т ) Gz (z, z', т) Gx (х, х', т) =----• exp 2 • V пат ^ (x - x' + V •т)2 к 4 ат v Gy(у, у',т) = п 1• exP 2 • ^пат - (y — у) к 4 ат у Gz ( z, z *, т ) = 2 • да •I n=—да exp к к (z — z' + 2 n3 )2 4ат + exp к (z + z + 2 nsf 4ат (5)-(8) Одномерные функции Грина подбираются исходя из краевых условий. Для оценки характера распределения температурных полей при ЭЛС можно использовать математическую модель, в которой тепловое воздействие электронного луча рассматривается как воздействие непрерывно действующего комбинированного источника [1, 3, 4]. В рамках данного исследования использовались два типа комбинированных источников: 1) ЭЛ С с колебаниями луча поперёк стыка с амплитудой A - непрерывно действующий линейный по глубине (вдоль оси z, длиной h) и линейный вдоль оси у (длиной 2А) нормально распределённый источник, вводимый в начале координат, действующий в течение определённого отрезка времени t: F 1(x, y, z, т) = q1 • | k1- • Ж(x')E(y Жz')E(т) + k2- • Ж(x')E(y')E(z')E(т) | cp к2A 2Ah J , [1_ при _ — A< y '< A [1_ при _0 < z '< h [1_ при _ t0 < т< t E(y)=L л - /E(z)=L i • n;E(т)=L [0_ при _ A < y<— A [0_ при _ h< z < 0 [0_ при _ т > t 2) ЭЛС с X-образными колебаниями луча с амплитудой b - непрерывно действующий линейный по глубине (вдоль оси z, длиной h) и прямоугольный (2bх2b) на поверхности, нормально распределённый источник, вводимый в начале координат, действующий в течение определённого отрезка времени t: F2(x, y, z, т) = q^ • | k1^ • E(x')E(y'Жz')E(т) + k2- • E(x')E(y')E(z')E(т) cp к4b2 4b2h E (x') = 1_ при _ — b< x' < b 0_ при _ b< x'< — b ; e (y') = 1_ при _ — b< y' < b 0_ при _ b< y' < — b ’ E (z') Распределение мощности луча q между поверхностным и линейным по глубине источником осуществляется за счёт введения коэффициентов распределения энергии к1 и к2 соответственно. Среднее значение коэффициентов к1= 0,2-0,3 и к2=0,7-0,8 [1]. Для имитации воздействия нормально-кругового источника рассчитывается время действия фиктивного источника: 10 = 4 aK K = 22 d2 Судить о величине заглубления линейного источника можно по расчётной глубине проплавления, которая связана с параметрами ЭЛС критериальным уравнением: H = a(, (n • q)k V0,5k—1d ".5k (^^ Tпл )k коэффициент сосредоточения для заданного диаметра электронного луча: где величина к = 0,68 • (Я • Тпл )0,15, а - температуропроводность, λ – теплопроводность, Тпл – температура плавления, η – эффективный КПД, q – мощность теплового потока, V – скорость сварки, d – диаметр луча. Таким образом, запишем интегральное решения уравнения переноса энергии относительно функции первого источника, которое описывает математическую модель ЭЛС с поперечными колебаниями луча: к 1 • qn 1 T1(х, у, z, т) = - • exp 8АпЯ т t0 — V 4 ат 9 (x + V • т)2 ) (x + V • т)2 4 ат / (z+ 2n5)2 ) 4 ат7 9т + к 2 • qn 16 Ahcp • vna t 9 J—exp t о т V • Е exp n =-О> \ ” •Е n=—« erf z + h + 2n5 V 2 • Vor erf —h+2n5 2 • 40т ) 9т Аналогично запишем интегральное решение переноса энергии относительно функции второго источника, которое описывает математическую модель ЭЛС с Х-образными колебаниями луча: T 2( х, у, z, т) = к 1 • qn t J • erf x + b + V • т V — erf x — b + V • т + к2 • qn t erf V V x + b + V • т A — erf Л Л — • V от — erf y — b • Е exp n = : —ОТ V — V V V 32b2hcp • I V • V t0 — erf x — b + V • т — V V V (z+2n5) 4 ат дт + y erf +b A — CO erf z + h + 2 n5 A — y — b ■Е n= : —ОТ — V дт V erf z — h + 2 n5 V Поскольку границей раздела двух материалов будет ось y, области лежащей слева, т.е. при y<0 присваиваются значения теплофизических характеристик первого материала (с1,λ1,ρ1,а1), а области лежащей справа, т.е. при y>0 присваиваются значения теплофизических характеристик второго материала (с2,λ2, ρ2,а2). В качестве допущения присваиваем среднее значение теплофизические характеристики материалов при y=0. Теплофизические характеристики свариваемых материалов представлены в табл. 1. Таблица 1. Теплофизические характеристики материалов Теплофизические характеристики Сталь (12Х21Н5Т) Бронза (БрХ08) коэффициент теплопроводности λ, Дж/(с·м·K) 25 260 плотность ρ, кг/м3 7650 8900 теплоёмкость c, Дж/(кг·K) 528 480 температура плавления, ОС Расчёт температурных полей производился в программе MathCAD 15. Листинг состоит из нескольких последовательных этапов: 1) Присвоение переменным значений режима сварки (ускоряющее напряжение, ток луча, диаметр луча на поверхности, скорость сварки, время сварки) и теплофизических характеристик свариваемых материалов (теплопроводность, плотность, теплоёмкость). 2) Предварительный расчёт глубины проплавления на основе исходных данных для определения величины заглубления линейного источника. Расчёт дополнительных параметров (коэффициент сосредоточения K и время действия фиктивного источника t0). 3) Расчёт температурных полей по координатным плоскостям X-Y и Y-Z. Результаты моделирования и сравнение с экспериментальными данными. Расчетные данные были сопоставлены с образцами, сваренными из стали 12Х21Н5Т (толщина 7,5мм) с бронзой БрХ08 (толщина 5,5мм), соединение в замок. Образцы были сварены по следующим режимам: - образец №1 – I=32-34 мA; U=60 кВ; Vсв=5 мм/сек; поперечные колебания амплитудой 0,8 мм. - образец №2 – I=32-35 мA; U=60 кВ; Vсв=5 мм/сек; X-образные колебания амплитудой 0,8 мм. Образец №1. Расчётные температурные поля в плоскости X-Y при z=0 (на поверхности) представлены на рисунке 1 (1 деление – 0,5мм). Рис. 1. Распределение температурных полей в плоскости X-Y при z=0 Максимальная ширина зоны, нагретой до температуры плавления, в стали смещена относительно координаты x=0. Это связано с большей тепловой инерцией стали по сравнению с бронзой. Для получения достоверных данных по параметрам шва необходимо производить расчёт тепловых полей в плоскости Y-Z при x=0 (для определения ширины шва по бронзе) и при смещении на 1,25 мм (для определения ширины шва по стали). Совместив графики температурных полей можно получить максимально приближенную форму шва. Сравнение экспериментальной и расчётной формы шва первого образца представлено на рис. 2, расхождение экспериментальных и расчётных данный по ширине шва составляет 8%, по глубине проплавления – 1,5%. Образец №2. Расчётные температурные поля в плоскости X-Y при z=0 представлены на рис. 3. Для получения данных по параметрам шва, необходимо производить расчёт тепловых полей в плоскости Y-Z при x=0 (для определения ширины шва по бронзе) и при смещении на 1,75 мм (для определения ширины шва по стали). Сравнение экспериментальной и расчётной форм шва второго образца представлено на рис. 4, расхождение экспериментальных и расчётных данный по ширине шва составляет 10%. Рис. 2. Сравнение экспериментальной (слева) и расчётной (справа) формы шва Рис. 3. Распределение температурных полей в плоскости X-Y при z=0 Рис. 4. Сравнение экспериментальной (слева) и расчётной (справа) формы шва Выводы: 1. Получена математическая модель для расчётов температурных полей при электроннолучевой сварке разнородных материалов с осцилляцией луча (поперечные и Х-образные колебания). 2. Расчётные температурные поля, полученные при помощи данной модели, позволяют судить о геометрии сварных швов с точностью достаточной для инженерных расчётов. Работа выполнялась при поддержке грантов Российского Фонда Фундаментальных Исследований РФФИ-Урал № 11-08-96016 и 13-08-00397 и при финансовой поддержке министерства образования Пермского края. 1. 2. 3. 4.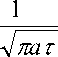
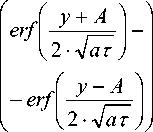
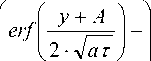
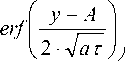

Список литературы Моделирование тепловых процессов при электронно-лучевой сварке разнородных материалов
- Язовских, В.М. Математическое моделирование и инженерные методы расчета в сварке: в 2 ч. Ч. 2. Тепловые процессы при сварке и моделирование в пакете MathCad. -Пермь: Изд-во ПГТУ, 2008. 119 с.
- Рыкалин, Н.Н. Расчёты тепловых процессов при сварке. -М.: Машгиз, 1951. 296 с.
- Рыкалин, Н.Н. Основы электронно-лучевой обработки материалов/Н.Н. Рыкалин, А.А. Углов, И.В. Зуев. -М.: Машиностроение, 1978. 239 с.
- Рыкалин, Н.Н. Лазерная и электронно-лучевая обработка материалов: справочник/Н.Н. Рыкалин, А.А. Углов, И.В. Зуев, А.Н. Кокора. -М.: Машиностроение, 1985. 496 с.


