Моделирование термодинамических свойств известково-глинозёмистых расплавов

Тюрин Александр Георгиевич; Працкова Светлана Евгеньевна; Tyurin Aleksandr Georgievich; Pratskova Svetlana Evgenyevna

Научные статьи \ Математика. Естественные науки \ Химия. Кристаллография. Минералогия \ Физическая химия

Моделирование термодинамических свойств известково-глинозёмистых расплавов

Автор: Тюрин Александр Георгиевич, Працкова Светлана Евгеньевна

Журнал: Вестник Южно-Уральского государственного университета. Серия: Химия @vestnik-susu-chemistry

Рубрика: Физическая химия

Статья в выпуске: 1 (260), 2012 года.

Бесплатный доступ

Рассчитаны избыточные энтальпии, энтропии, энергии Гиббса расплавов системы СаО-Ai 2О 3 в интервале температур 1500-1800 °С. Термодинамические свойства согласованы с наиболее достоверными экспериментальными данными по энергиям Гиббса реакций образования алюминатов кальция, термодинамическим характеристикам плавления чистых оксидов и фазовой диаграмме состояния.

Известково-глинозёмистые расплавы, избыточные термодинамические свойства, обобщённая теория "регулярных" ионных растворов

Короткий адрес: https://sciup.org/147160214

IDR: 147160214 | УДК: 544-971+669.14

Modeling thermodynamic characteristics of calciferous-aluminous melts

It is calculated excess enthalpies, entropies, Gibbs energies of melts of the system СаО-Аl 2О 3 in interval of the temperature 1500-1800 °С. Thermodynamic characteristics are coordinated with the most reliable experimental given on Gibbs energies reactions of the formation aluminates calcium, thermodynamic features of the melting undiluted oxides and phase diagram.

Текст научной статьи Моделирование термодинамических свойств известково-глинозёмистых расплавов

Термодинамические свойства расплавов системы CaO–Al 2 O 3 представляют значительный интерес для металлургии, технологий керамических материалов и цемента. Для их определения проведено значительное количество экспериментальных исследований [1–12]. Однако достоверные термодинамические данные в области высоких температур (выше 1800 K) практически отсутствуют.

У диаграммы состояния системы CaO–Al 2 O 3 до сих пор не существует общепринятой версии; разные её варианты отличаются составом и количеством алюминатов кальция и их устойчивостью. В бескислородной атмосфере система характеризуется образованием четырёх промежуточных фаз (рис. 1): СА 6 , СА 2 , СА и С 3 А (С – CaO, А – Al 2 O 3 ).

Энергии Гиббса реакций образования алюминатов кальция из простых оксидов по данным разных авторов сильно отличаются друг от друга, особенно их зависимости от температуры. Наиболее достоверные значения были получены в работе [1] масс-спектрометрическим эффузионным методом Кнудсена (табл. 1). Принятые значения термодинамических величин, характеризующие процессы плавления оксидов кальция и алюминия, следующие [14]:

A m H ( CaO ) = 52 кДж/моль, T ^ ( CaO ) = 2900 K;

A m H ( Al₂O₃ ) = 111,4 кДж/моль, T ( Al₂O₃ ) = 2327 K.

Таблица 1

Стандартные энергии Гиббса реакций образования алюминатов кальция из оксидов при 1833–2033 К [1]

№ п/п	Реакция*	A r G T =A r H T - T A _rS_T, Дж
1	3CaO(т)+Al 2 O 3 (т)=3CaO∙Al 2 O 3 (т)	14720–18,14 Т
2	CaO(т)+Al 2 O 3 (т)=CaO∙Al 2 O 3 (т)	22900–28,10 Т
3	CaO(т)+2Al 2 O 3 (т)=CaO∙2Al 2 O 3 (т)	–6300–9,94 Т
4	CaO(т)+6Al 2 O 3 (т)=CaO∙6Al 2 O 3 (т)	–2880–5,00 Т

* – стандартное состояние оксидов – чистый твёрдый компонент.

Результаты расчётов и их обсуждение

Разными авторами при моделировании термодинамических свойств известковоглинозёмистых расплавов использовались модели молекулярных ассоциированных растворов [5], регулярных [15] и субрегулярных [16, 17] ионных растворов. При этом возникали принципиальные проблемы в согласовании фазовых диаграмм состояния с термодинамическими свойствами фаз, установленными другими авторами. Так Д.М. Лаптев, рассчитывая диаграмму плавкости CaO–SiO 2 [18], ввёл понятие о «термохимической» теплоте плавления CaO, которая отличается от термодинамической и особым «расчётным» способом меняется с температурой.

В настоящей работе рабочей моделью системы была выбрана обобщённая теория «регулярных» ионных растворов [19]. За счёт концентрационной и температурной зависимостей энергии смешения компонентов эти проблемы согласования здесь снимаются.

Активности компонентов расплавов CaO–Al 2 O 3 описывали формулами:

RT In a ( CaO ) ж = RT In x ^ + x 22 Г 2 x ^ ■ Q ^ ( T ) + ( 1 - 2 x_x ) ■ Q . 2 ( T ) + x_x ( 2 - 3 x ^ ) ■ Q ^ ( T ) 1 ; (1)

71 T’ 1 / A 1 Z~\ \ 71 T’ 1 2 . 'I 2 / 1 'I \ /1 ( 1 ) / T’A . 'I Zll 2 ) / rp \ / >1 1 \ /ll 3 ) / гт-г \ /''I \

RT ln ^a( Al 2 O 3 ) ж = RT ln x 2 ⁺ ² x 1 ^Г( 1 ^- ² x 2 ) ■ ^Q 12 ( T ) ⁺ ² x 2 ■ Q 12 ( ^T ) ⁺ x 2 ( ² ^- ³ x 2 ) ■ Q 12 ( ^T ) J ^{. (2)}

^N 2 ^N 2+ 3+

Здесь x =---¹— , x ₂ =---²-- ионные доли катионов кальция (Ca ) и алюминия (Al ); N ₁ и N 2 -

¹ 1 + N ₂ ² 1 + N ₂

мольные доли CaO и Al ₂ O ₃ в расплаве; Q yk ) ( T ) - энергетические параметры модели.

Оценка значений энергетических параметров компонентов Q ^k )( T ) проводилась путём обработки экспериментальных данных по фазовой диаграмме состояния (см. рис. 1) с учётом данных табл. 1 и характеристик процесса плавления простых оксидов [14]. Значения параметров описываются полиномами четвёртого порядка относительно температуры и охватывают область температур 1600–3000 K:

Q 1 ⁽ 2 ) = -5,3 • 10 7 + 136 800 Т - 130,18 Т ² + 0,055 Т ³ - 8,8• 10 ^-6 Т ⁴, Дж/моль;

Q 1 ⁽ ₂ ² ⁾ = 2,27-10 ⁷ - 33 800 Т + 20,37 Т ² - 0,006 Т ³ + 7,85• 10 ^-7 Т ⁴, Дж/моль;

Q 1 ⁽ ₂ ³ ⁾ = -7,2-10 7 + 97 000 Т - 42,20 Т ² + 0,004 Т ³ + 1,2-10 ⁶ Т ⁴, Дж/моль.

Результаты расчётов фазовых равновесий в системе CaO–Al 2 O 3 представлены на рис. 1. Линия ликвидус расчётной диаграммы состояния практически сливается с экспериментальной, что свидетельствует о применимости используемой модели раствора для описания термодинамических свойств расплавов.

Избыточную энергию Гиббса известково-глинозёмистых расплавов описывали уравнением [19]

= x 1 x 2 x 1 ■ Q 2 ⁽ T ) + x 2 ■ Q y^ ⁽ T ) + x 1 x 2 ■ Q^ ⁽ T ) .

Избыточную энтальпию и энтропию жидкого раствора оценивали по уравнению Гиббса– Гельмгольца:

H^E =- T ²

E д —

l T J

; S E =- ( G. ) . (4)

^{l д} T ^J P , X i

P , X_i

∂ T

В интервале температур 1500–1800 °С данные расчётов приведены в табл. 2 и на рис. 2–4. В рассматриваемом интервале температур и в области гомогенности оксидных расплавов избыточная энергия Гиббса отрицательна и по абсолютной величине не превышает 100 кДж моль . При ионной доле алюминия х 2 меньше 0,65 при всех температурах растворы образуются с выделением тепла и с упорядочением, что указывает на процессы ассоциации компонентов в расплавах CaO–Al 2 O 3 . При дальнейшем увеличении содержания глинозёма в расплаве с ростом температуры проявляется отчётливая тенденция к расслоению подобно системе CaO–SiO 2 [18]. В целом модельные значения термодинамических свойств известково-глинозёмистых расплавов не противоречат имеющимся экспериментальным данным [1–12].

Таблица 2 Результаты расчетов избыточных термодинамических функций известково-глинозёмистых расплавов

x 1	x 2	G^E , кДж/моль	S^E , Дж/моль·K	H^E , кДж/моль
1	2	3	4	5
t = 1500 °С
0,54	0,46	–12,09	–28,46	–62,56
0,52	0,48	–13,08	–20,90	–50,14
0,5	0,5	–13,87	–14,71	–39,94
0,48	0,52	–14,46	–9,93	–32,07
0,46	0,54	–14,84	–6,63	–26,59
0,44	0,56	–15,02	–4,80	–23,52
0,425	0,575	–15,01	–4,39	–22,78
t = 1600 °С
0,6	0,4	–17,45	–135,39	–271,03
0,58	0,42	–17,54	–117,84	–238,24
0,56	0,44	–17,55	–100,88	–206,50
0,54	0,46	–17,50	–84,75	–176,23
0,52	0,48	–17,37	–69,65	–147,82
0,5	0,5	–17,18	–55,74	–121,57
0,48	0,52	–16,92	–43,16	–97,77
0,46	0,54	–16,61	–32,04	–76,63
0,44	0,56	–16,23	–22,46	–58,29
0,42	0,58	–15,79	–14,46	–42,88
0,4	0,6	–15,31	–8,08	–30,43
0,38	0,62	–14,76	–3,30	–20,95
0,36	0,64	–14,18	–0,11	–14,38
0,34	0,66	–13,54	1,57	–10,59
0,333	0,667	–13,31	1,82	–9,90
t = 1700 °С
0,59	0,41	–35,86	–251,25	–531,58
0,57	0,43	–33,72	–224,09	–475,85
0,55	0,45	–31,55	–197,20	–420,62
0,53	0,47	–29,40	–170,90	–366,58
0,51	0,49	–27,27	–145,50	–314,34
0,49	0,51	–25,21	–121,26	–264,45

Окончание табл. 2

1	2	3	4	5
0,47	0,53	–23,22	–98,41	–217,39
0,45	0,55	–21,32	–77,16	–173,56
0,43	0,57	–19,53	–57,67	–133,32
0,41	0,59	–17,86	–40,08	–96,93
0,39	0,61	–16,31	–24,48	–64,62
0,37	0,63	–14,90	–10,95	–36,51
0,35	0,65	–13,62	0,48	–12,68
0,33	0,67	–12,47	9,80	6,87
0,31	0,69	–11,46	17,05	22,19
0,29	0,71	–10,57	22,29	33,41
t = 1800 °С
0,59	0,41	–70,33	–453,30	–1010,02
0,56	0,44	–62,05	–391,76	–874,16
0,53	0,47	–53,79	–329,92	–737,73
0,5	0,5	–45,78	–269,39	–604,22
0,47	0,53	–38,19	–211,53	–476,69
0,44	0,56	–31,19	–157,53	–357,75
0,41	0,59	–24,88	–108,38	–249,56
0,38	0,62	–19,36	–64,86	–153,81
0,35	0,65	–14,69	–27,54	–71,78
0,32	0,68	–10,87	–3,18	–4,28
0,29	0,71	–7,91	–27,13	48,33
0,26	0,74	–5,76	44,32	86,12
0,23	0,77	–4,33	54,98	109,63
0,2	0,8	–3,53	59,51	119,84
0,19	0,81	–3,37	59,76	120,52

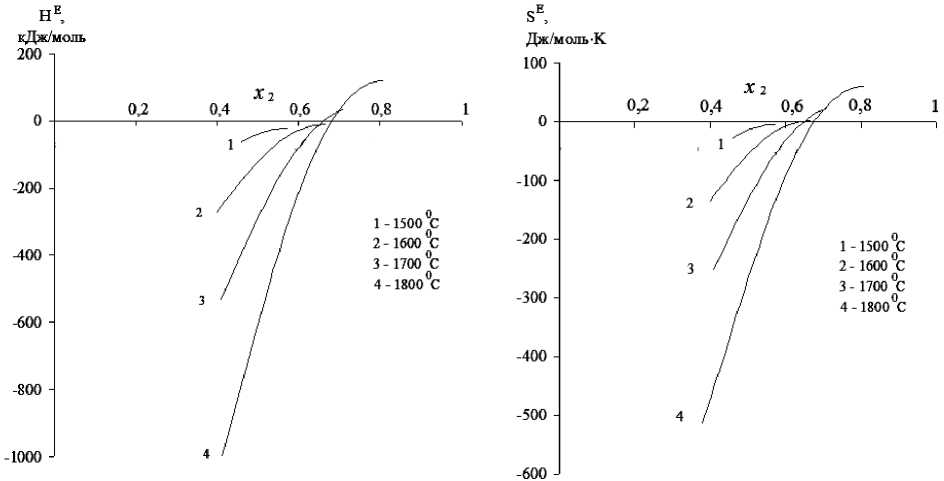
Рис. 2. Избыточная энтальпия известково-глинозёмистых расплавов в интервале температур 1500–1800 °С

Рис. 3. Избыточная энтропия известково-глинозёмистых расплавов в интервале температур 1500–1800 °С

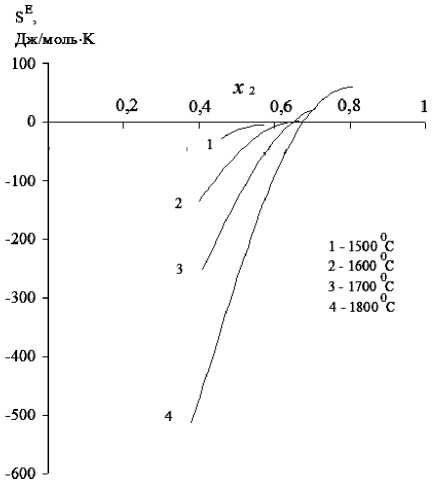
Рис. 4. Избыточная энергия Гиббса известковоглинозёмистых расплавов в интервале температур 1500–1800 °С

Заключение

1. Показана применимость обобщённой теории «регулярных» ионных растворов для аналитического описания термодинамических свойств известково-глинозёмистых расплавов.
2. Выведены выражения для активностей и избыточных термодинамических функций расплавов системы CaO–Al 2 O 3 в интервале температур 1600–3000 K.

Список литературы Моделирование термодинамических свойств известково-глинозёмистых расплавов

Шульц, М.М. Масс-спектрометрическое исследование термодинамических свойств расплавов алюминатов кальция/М.М. Шульц, С.И. Шорников//Доклады Академии Наук. -1995. -Т. 340, № 3. -С. 350-352.
Nagata, K. Activity of components in oxide melts CaO-Al2O3/K. Nagata, J. Tanabe, K.S. Goto//Proc. VI Int. Iron and Steel Congr. Nagaya, Japan. -1990. -Vol. 1. -Р. 217-224.
Fujisawa, T. Thermodynamics of liquid CaO, Al2O3/T. Fujisawa, C. Yamauchi, A. Sakao//Proc. VI Int. Iron and Steel Congr. Nagaya, Japan. -1990. -Vol. -Р. 201-208.
Rog G. Thermodynamic functions of calcium aluminate/G. Rog, A. Kozlowska-Rog, K. Zakula-Sokol//J. Chem. Thermodyn. -1993. -Vol. 25, № 7. -Р. 807-810.
Зайцев, Ф.И. Термодинамические свойства и фазовые равновесия в системе CaF2-Al2O3-CaO/Ф.И. Зайцев, Н.В. Королёв, Б.М. Могутнов//I Советско-чехословацкий симпозиум по теории металлургических процессов: тез. докл. -1989. -Ч. 1. -С. 82-87.
Ghosh, D. Standard Free Energy of Formation of Alumina/D. Ghosh, D.A.R. Kay//Electrochem. Soc. -1977. -Vol. 124, № 12. -Р. 1836-1845.
Chemical and phase equilibria in the CaO-Al2O3 system/K. Adamkovicova, L. Rosa, S. Porvas, I. Proks//Chem. Papers. -1985. -Vol. 39, № 1. -Р. 3-13.
Thermodynamic properties of CaO-Al2O3 liquid solution/M. Allibert, C. Chatillon, K.T. Jacob, R. Lourtan//J. Amer. Ceram. Soc. -1981. -Vol. 64, № 5. -Р. 307-314.
Чемекова, Т.Ю. К вопросу о характере диаграмм состояния системы CaO-Al2O3/Т.Ю. Чемекова, Ю.П. Удалов//Изв. АН СССР. Неорган. материалы. -1974. -Т. 10, № 12. -С. 2191-2193.
Nurse R.W., Welch J.H., Majumdar A.J.//Trans. Brit. Ceram. Soc. -1965. -Vol. 64, № 9. -Р.409-418.
Rein, R.H. Activities in liquid slags CaO-Al2O3/R.H. Rein, J. Chipman//Trans. Met. Soc. AIME. -1965. -Vol. 233, № 2. -Р. 415-425.
Sharma, R.A. Thermodynamic study of СаО-Л12О3 liquid slags/R.A. Sharma, F.D. Richardson//J. Iron and Steel Inst. -1961. -Vol. 198, № 4. -Р. 386-390.
Бережной, А.С. Диаграмма состояния многокомпонентных окислов/А.С. Бережной. -Киев: Наукова думка, 1970. -544 с.
Термодинамические свойства индивидуальных веществ: справ./под ред. Л.В. Гурвич. -М.: Наука, 1981. -Т. 3. -Кн. 1. -С. 472.
Кожеуров, В.А. Термодинамика металлургических шлаков/В.А. Кожеуров. -Свердловск: Металлургиздат, 1955. -163 с.
Срывалин, И.Т. Активности компонентов в оксидных системах/И.Т. Срывалин, О.А. Есин//Известия вузов. Черная металлургия. -1959. -№ 8. -С. 3-7.
Вильгельм, Е.М. О применении термодинамики ионных расплавов/Е.М. Вильгельм, Г.Г. Михайлов//Физико-химические исследования металлургических процессов. -Свердловск: УПИ, 1978. -Вып. 6. -С. 63-69.
Лаптев, Д.М. Расчёт диаграммы плавкости СаО-SiO2/Д.М. Лаптев//Известия вузов. Чёрная металлургия. -1970. -№ 6. -С. 10-13; 1970. -№ 8. -С. 7-11.
Тюрин, А.Г. Обобщённая теория «регулярных» растворов/А.Г. Тюрин//Труды XI Российской конференции «Строение и свойства металлических и шлаковых расплавов»: тез. докл. -Челябинск: ЮУрГУ, 2004. -С. 96-97.

Еще