Моделирование термоэмиссионной тепловой защиты при конвективном нагреве составной оболочки

При конструировании высокоскоростных летательных аппаратов (ВЛА) актуальной является задача, связанная с созданием систем тепловой защиты от конвективного нагрева. Известно достаточно различных методов пассивной, активной и комбинированной тепловых защит [1–3].

По-видимому, одним из перспективных направлений развития тепловой защиты может быть способ, основанный на термоэмиссионном методе [4–8]. В работах [4, 5] впервые в мире предложено применять явление термоэлектронной эмиссии в системе тепловой защиты ВЛА. В то же время первая статья [6] в США по этой теме датируется позже. Однако, судя по публикациям [6–8], в США уделяют данному направлению значительное внимание.

Данный метод позволяет преобразовать тепловую энергию, полученную при нагреве оболочки ВЛА, непосредственно в электрическую. При этом испарение тепловых электронов с эмиттера и превращение части тепловой энергии в электрическую сопровождается понижением температуры электрода [9, 10]. В системе тепловой защиты, основанной на термоэмиссионном методе, протекает множество взаимосвязанных процессов [9]: эмиссионных, электрических, плазменных, тепловых, адсорбционных и др. Экспериментальные исследования термоэмиссионных установок довольно сложны и дорогостоящи [11], поэтому уделяется большое внимание математическому моделированию протекающих в них процессов [5, 9, 12]. В данной работе представлена и исследована модель термоэмиссионной тепловой защиты (ТЭТЗ). Показано, что выбором параметров защиты возможно существенно уменьшить температуру ее конструкций.

Постановка задачи

Пусть имеется многоэлементная конструкция из электрогенерирующих элементов (ЭГЭ) и у каждого из них своя зона влияния с характерным размером Lk. С целью упрощения анализа рассмотрим один ЭГЭ в виде слоеного аксиально симметричного цилиндра с небольшой долей конусности. На рис. 1 схематично представлены слои активной защиты для фиксированного аксиального угла со своей зоной влияния и характерным поперечным размером Lk = sk – sA. Исследуем задачу о теплообмене внутри типичного ЭГЭ, под которым будем понимать составную область с теплоизолированной стенкой при s = sA 0 ≤ n ≤ L2 (кроме коллектора L4 ≤ n ≤ L5) и s = sk L5 ≤ n ≤ L8 (кроме эмиттера L2 ≤ n ≤ L3). Координата n направлена от поверхности вглубь оболочки (рис. 1), где 1-й слой — внешняя область из тугоплавкого сплава молибдена и вольфрама (Мо (85%) + W (15%)) [13]; 2-й слой — эмиттерная изоляция из карбида циркония; 3-й слой включает изолятор 2, эмиттер из вольфрама 3 и вольфрамовый токоввод 3; 4-й слой состоит из молибденового токовывода 4, коллектора из молибдена 4 и изолятора 5; 5-, 7-й — емкость теплоносителя из Al2O3; 6-й — охлаждающий воздух или гелий; 8-й — потребитель электрический энергии (электрическая нагрузка); эмиттер 3 и коллектор 4 составляют термоэмиссионный элемент, через d обозначена величина межэлектродного зазора (МЭЗ); Lj, j = 1, …, 8 — расстояния от начала координат по n областей 1–3, зазора, областей 4–7; δj, j = 1, …, 7 — толщины областей 1–7 на рис. 1.

Исследование характеристик ЭГЭ основывается на вольт-амперных характеристиках (ВАХ) изотермического термоэмиссионного преобразователя (ТЭП) [9–12, 14], которые, в свою очередь, являются интегральными характеристиками многообразных процессов в МЭЗ и на электродах [9, 14] и определяются переносом частиц и энергии в плазме, ионизационными, адсорбционными и другими процессами. Математическая формулировка электрической модели взята из работы [12], но рассмотрен общий случай: потенциал вдоль коллектора изменяется, электропроводность электродов и коммутационных деталей зависит от их температуры.

Для нахождения прототипов ВЛА, на которых может быть оправдана установка ТЭТЗ, желательно найти уровень тепловых потоков, снимаемых с внешней открытой оболочки эмиттера (область 3 на рис. 1) и внешней поверхности коллектора (область 4 на рис. 1) за счет электронного охлаждения и процессов излучения. Кроме того, надо знать высокоэнтальпийные потоки от аэродинамического нагрева внешней части тугоплавкого металла (область 1 на рис. 1). Тепловые потоки для внешних открытых частей областей 3 и 4 имеют вид [9, 12]:

q_{L 3} = –( q ₁ + q _ε + q _Cs), q_{L 4} = q ₂ + q _ε + q _Cs;        (1)

q ₁ = J ( T _2,4, T _1,3, Δ V )[ ϕ ₁( T _1,3/ T _Cs)/ e + 2 kT _1,3/ e ]; (2)

q ₂ = J ( T _2,4, T _1,3, Δ V )[ ϕ ₂( T _2,4/ T _Cs)/ e + 2 kT _1,3/ e ]; (3)

q ε = σε s ( T 1 ⁴ ,3 – T 2 ⁴ ,4 ), q Cs = ( λ Cs / d )( T 1,3 – T 2,4 ).     (4)

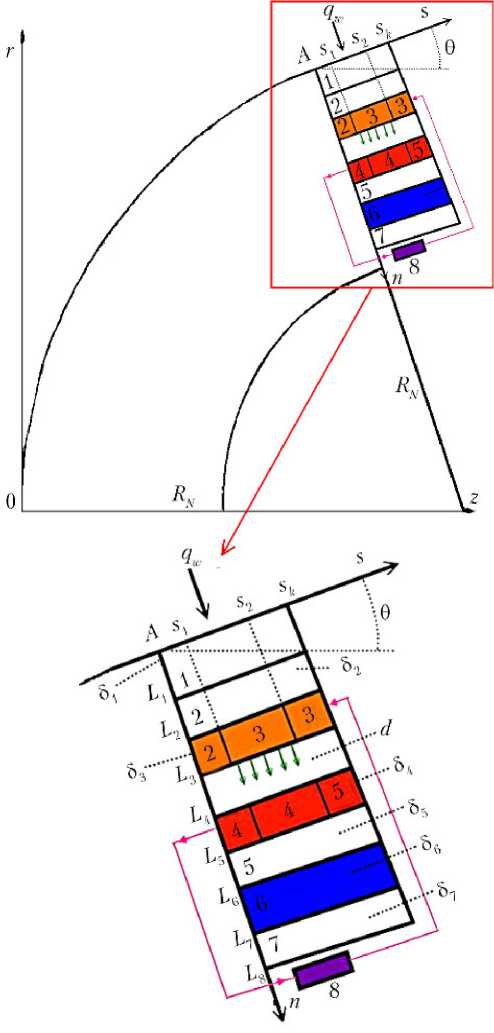
Рис. 1. Схема конструкции с электрогенерирующим элементом

В формулах (1)–(4) k — постоянная Больцмана; e — заряд электрона; σ — постоянная Стефана–Больцмана; T — температура; T2,4, T1,3 — температуры внешней поверхности коллектора и внутренней поверхности эмиттера; λCs — коэффициент теплопроводности пара цезия в межэлектродном зазоре; J = J(T2,4, T1,3, ΔV) — ВАХ изотермического ТЭП; ΔV — разность потенциалов между эмиттером и коллектором; ϕj, j = 1, 2 — эффективная работа выхода электронов эмиттера и коллектора; εs — приведенная излучательная способность поверхностей эмиттера и коллектора. Индексы: нижние 1 и 2 в левой части формул (2) и (3) соответствуют параметрам эмиттера и коллектора, Cs — пару цезия; A — граница сопряжения сфера–конус на рис. 1; k — конечное значение по координате s.

Задача расчета характеристик теплообмена с использованием естественных координат сводится к решению системы уравнений [2] при s_A <  s <  s_k :

∂ T c pj ( T 1, j ) ρ j   ∂ t ^{1 , j}

∂

= λ ( T )

_∂ n      j 1, j

^{∂ T} 1, j ∂ n

∂

+ _{∂ s}    λ j ( T 1, j )

^{∂ T} 1, j ∂ s

+

λ(T )   ∂T          ∂T j 1, j 1, j sinθ –       1, j

r

∂ s

∂ n

cos θ ;

j = 1, 2; 0 <  n <  L ₂; s_A <  s <  s_k ;

∂T cp2(T1, 3)ρ2   ∂ t1 , 3

∂

λ ( T ) _∂ n    2   1, 3

^{∂ T} 1, 3 ∂ n

∂

⁺   ∂ s    λ 2 ( T 1, 3 )

^{∂ T} 1, 3 ∂ s

+

^λ 2 ^{( T} 1, 3 ^{)     ∂ T} 1, 3

r

∂ s

∂ T _{1 3} sin θ –       ^,

∂ n

cos θ ;

L ₂<  n <  L ₃; s_A <  s <  s ₁;

^{∂ T} 1, 3 c p 3 ( T 1, 3 ) ρ 3    _∂ t

∂

λ ( T ) _∂ n    3   1, 3

^{∂ T} 1, 3 ∂ n

∂

+ _{∂ s}   λ 3 ( T 1, 3 )

^{∂ T} 1, 3 ∂ s

+

^λ 3 ^{( T} 1, 3 ^{)     ∂ T} 1, 3

r

∂ s

sin θ –

^{∂ T} 1, 3 ∂ n

cos θ + P ₁ ^V ;

L ₂<  n <  L ₃ ; s ₁

< s <  s_k ;

^{∂ T} 2 4 c p 4 ( T 2, 4 ) ρ 4    _∂ t ^,

∂

λ ( T ) _∂ n    4   2, 4

^{∂ T} 2, 4 ∂ n

∂

+ _{∂ s}   λ 4 ( T 2, 4 )

^{∂ T} 2, 4 ∂ s

+

^λ 4 ^{( T} 2, 4 ^{)     ∂ T} 2, 4

r

∂ s

sin θ –

^{∂ T} 2, 4 ∂ n

cos θ + P ₂ ^V ;

L ₅<  n <  L ₆; s_A <  s <  s ₂;

^{∂ T} 2, 4 c p 5 ( T 2, 4 ) ρ 5    _∂ t

∂

λ ( T ) _∂ n    5   2, 4

^{∂ T} 2, 4 ∂ n

∂

+ _{∂ s}   λ 5 ( T 2, 4 )

^{∂ T} 2, 4 ∂ s

+

^λ 5 ^{( T} 2, 4 ^{)    ∂ T} 2, 4

r

∂ s

sin θ –

^{∂ T} 2, 4 ∂ n

cos θ ;

L ₅<  n <  L ₆; s ₂<  s <  s_k ;

∂ T c pj ( T 2, j ) ρ j   ∂ t ^{2 , j}

∂

λ ( T ) _∂ n      j 2, j

2, j

^{∂ T} 2, j ∂ n

∂

⁺ ∂ s   λ j ( T 2, j )

^{∂ T} 2, j ∂ s

+   ^{λ j ( T 2, j )}

r

∂ T

^{2, j} sin θ – ∂ s

^{∂ T} 2, j

^, cos θ ;

∂ n

L6 < n < L8; sA < s < sk; j = 5, 6, 7, где r = (RN – n)cosθ + (s – sA)sinθ; t — время; cpj, λj, ρj, j = 1, …, 7 — коэффициенты удельной теплоемкости, теплопроводности и плотность слоев конструкций ТЭТЗ, соответственно; PiV(s) = ξiIi2(s)/Si2, i = 1, 2 — объемное джоулево тепловыделение эмиттера и коллектора; RN — радиус сферического затупления; θ — угол конусности.

Систему уравнений (5)–(10) необходимо решать с учетом следующих начальных и граничных условий.

Начальные условия:

T 1 | t =0 = T 0 , 0 ≤ n ≤ L 3 ;

T 2 | t =0 = T 0 , L 4 ≤ n ≤ L 8 ;

на обтекаемой внешней поверхности оболочки ( n = 0):

qw – ε1σT41w = –λ1(∂T1,1/∂n)|w, sA ≤ s ≤ sk;                (12)

на поверхности третьего слоя — изолятора ( n = L ₃, s_A ≤ s ≤ s ₁) выставляется условие теплообмена по закону Ньютона и учитывается отвод тепла от излучения поверхности карбида циркония

–λ2(∂T1,3/∂n)| n=L3 = Δ1(T1,3 | n=L3 – T1*) – ε2σT14 | n=L3, sA ≤ s ≤ s1;                 (13)

на поверхности третьего слоя — эмиттера ( n = L ₃) — согласно первой формуле (1):

qL3 = –λ1,3(∂T1,3 /∂n) | n=L3, s1 < s < s2;                (14)

на поверхности третьего слоя — эмиттера ( n = L ₃, s_A ≤ s ≤ s_k ) выставляется граничное условие третьего рода, и учитывается отвод тепла от излучения поверхности вольфрама

–λ3(∂T1,3/∂n)| n=L3 = Δ1(T1,3 | n=L3 – T1*) – ε1σT14 | n=L3, s2 ≤ s ≤ sk;                   (15)

на внешней поверхности четвертого слоя — коллектора ( n = L ₄, s_A ≤ s <  s ₁) имеет место теплообмен по закону Ньютона

–λ4(∂T2,4/∂n) | n=L4 = Δ2(T2,4 | n=L4 – T2*), sA ≤ s ≤ s1;                 (16)

на внешней поверхности четвертого слоя — коллектора ( n = L ₄, s ₁ ≤ s <  s ₂) — из второй формулы (1):

q L ₄ = – λ 4 ( ∂ T 2,4 / ∂ n ) | n=L ₄ , s 1 ≤ s <  s 2 ;    (17)

на внешней поверхности четвертого слоя — изолятора Al₂O₃ ( n = L ₄, s ₂ ≤ s ≤ s_k ) имеет место граничное условие третьего рода

–λ5(∂T2,4/∂n) | n=L4 = Δ2(T2,4 | n=L4 – T2*) , s2 ≤ s ≤ sk;                  (18)

на поверхности седьмого слоя — подложки ( n = L ₈) выставляется условие теплообмена по закону Ньютона

–λ7(∂T2,7/∂n) | n=L8 = δ(T2,7 | n=L8 – T0), sA ≤ s ≤ sk. (19)

На линиях сопряжения n = L_j , j = 1, 2 и n = L_i , i = 5, 6, 7 выписываются условия идеального контакта и равенства температур:

λ i

λ i-1

^d T 1, i

_{∂ n}

^{d T} 2, i

_{∂ n}

n-L -o = X +1

n = L j"" 0

= X.

i

T

^{d T} 1, i +1

_{∂ n}

^{d T} 2, i

_{∂ n}

n-L, -0     ^T 1, i +1

r.n, i = 1,2;

n - L . +0 ^{,           ,} ’

n-L +o, ¹ = ^5, 6 ^, 7;

, i = 1,2;

n-Lj +0 ^{,          ,} ’

^T 2, i -1 n-L -0 = ^T 2, i n-L, +0 ^{, 1} = ^{5, 6, 7}-

На левом ( s = s_A ) и правом ( s = s_k ) торцах 1–2 , 5–7 -го слоев имеет место условие тепловой изоляции

( ∂ T 1, i / ∂ s ) | s = s _A = 0, ( ∂ T 1, i / ∂ s ) | s = s _k = 0, i = 1, 2;

(∂T2,i /∂s) | s = sA = 0, (∂T2,i /∂s) | s = sk = 0, i = 5, 6, 7;                   (21)

на левом ( s = s_A ) и правом ( s = s_k ) торцах 4 -го слоя осуществляется теплообмен по закону Ньютона

– λ ₄( ∂ T _2,4/ ∂ s )| _s=sA = Δ ₂( T _2,4| _s=sA – T _2*);

– λ 5 ( ∂ T 2,4 / ∂ s )| s=s _k = Δ 2 ( T 2,4 | s=s _k – T 2* ),     ⁽²²⁾

на правом ( s = s_k ) торце эмиттера выставляется граничное условие третьего рода и учитывается отвод тепла от излучения поверхности вольфрама

– λ ₃( ∂ T _1,3/ ∂ s )| _s=sk = Δ ₁( T _1,3 | _s=sk – T _1*) – ε ₁ σ T ₁⁴_,3 | _s=sk , (23)

на линиях сопряжения s = s ₁ областей 2 , 3 на эмиттере и s = s ₂ областей 4 , 5 на коллекторе имеет место условие идеального контакта и равенства температур

∂ T

X=^T

81 2,4

⁴   d s

T

1,3 s=s ₁ -o

_S ^ _S 1-0

∂ T

1, 3

= Л,-----

³   d s

= _Л -^ ^ 2^

^S ^ ^S 2 ^{-0     5} d s

= T

1,3

• T s=s 1+0 ’ ^J2,4 s=s 2-0

.-. i ^+o;

S=S 2⁺0 ’

= T

2,4

S=S 2+0 ’

где T ₀ — начальная температура тела составной оболочки; ε _i , i = 1, 2 — излучательная способность поверхности вольфрама и карбида циркония; T _1*, T _2* — характерные температуры воздушной среды вблизи торца эмиттера при s = s_A и коллектора при s = s_k ; δ , Δ ₁, Δ ₂ — коэффициенты теплоотдачи составной конструкции с внешней средой.

Краевая задача (5)–(24) решена численно локально-одномерным методом расщепления [15]. При задании конвективного теплового потока из газовой фазы на конической части тела q_w воспользуемся формулами [16] для случая турбулентного режима течения в пограничном слое:

q_w = a _w ( h_{e 0} – h_w ); h_w = T _{1 w}c ₁ + c ₂ T ² _{1 w} /2;

16,4 ν ^1,5 ρ ^0,8          2,2 –p ( u / v )

∞∞           e m

.

R 0,2 (1 + h / h ) 2/3         ς 0,4 –r 0,2

N         w e 0                  2

ς = ( γ _ef – 1 + 2/M _∞ ²)/( γ _ef + 1);

p ^– = P_e / P_{e 0}; u_e / v_m = (1 – p ^{– χ} )^0,5;

Расстояния слоев оболочки вглубь по n (излучательные способности эмиттера, коллектора), их толщины, плотности, а также некоторые входные данные в уравнениях (4), (12), (13), (15), (16) даны в таблице.

Кроме распределения температурных полей составной оболочки ТЭТЗ необходимо найти самосогласованное решение электрической части модели. Для этого требуется знать распределение разности потенциала между эмиттером и коллектором Δ V = Δ V ( s ), которое в конечном итоге определяет рабочую точку ЭГЭ в составе тепловой защиты.

Для малых углов конусности θ ≤ 5 ° (sin θ < 0,1) распределение потенциала по длине электродов примет вид [9]:

χ = (γef – 1)/γef ; r2 = cosθ + (s – sA)sinθ, где ν∞ — скорость набегающего потока; h — энтальпия; M∞ — число Маха; ci, i =1, 2 — постоянные. Индексы: w соответствует параметрам внешней границы тела первого слоя; e и e0 — величинам на внешней границе пограничного слоя и в точке торможения тела; ∞ — величинам набегающего газового потока на бесконечности; черта «сверху» означает безразмерные параметры; z — время окончания теплового воздействия; ef — эффективную величину; 0 — начальную величину; m — максимальное значение; * — характерную величину.

Расчеты обтекания конуса с углом полураствора θ = 5 ° потоком химически равновесного воздуха проводились в формулах (25) для следующих условий, которые соответствуют Т ₀ = 273 К, высоте полета H _∞ = 3,0 ⋅ 10⁴ м и скорости ν_∞ = 3,36 ⋅ 10³ м/c. На этой высоте в работе [17] брались P _∞ = 1,197 ⋅ 10³ Н/м²; ρ_∞ = 1,84 ⋅ 10^–2 кг/м³; g _∞ = 9,73 м/с², и по формулам из источника [18] вычислялись h_{e 0} = 5,92 ⋅ 10⁶ Дж/кг; М _∞ = 13; g _ef = 1,21.

dV i ds

ξ

=       I i , i = 1, 2.

i

Если на участке эмиттера и коллектора плотность эмиссионного тока считать постоянной, то изменение силы тока эмиттера и коллектора вследствие термоэмиссии [9, 12]:

dI ₁ ds di ₂ ds

2п R i J ( T_M, T_u, A V );

- 2 n R 1 J ( T_гд, T 13 , A V ),

где R ₁ = R_N – L ₃ — внутренний радиус эмиттера; R ₂ = R_N – L ₄ — внешний радиус коллектора; S ₁ = 2 πδ ₃( R ₁ + δ ₃ /2); S ₂ = 2 πδ ₄( R ₂ – δ ₄ /2) — площади поперечных сечений эмиттера и коллектора; ξ _j, j = 1, 2 — электропроводность эмиттера и коллектора известна в зависимости от температуры [9]. Отметим, что ВАХ изотермического ТЭП зависят также от МЭЗ, давления насыщенного пара цезия, эффективной работы вы-

хода электронов эмиттера и коллектора.

Некоторые геометрические и тепловые характеристики термоэмиссионного преобразователя

Наименование характеристик	Номер слоя (см. рис. 1)
	1	2	3	4	5	6	7	8
δ i ×103, м	2	1	1	1	1	1	1
Li ×103, м	2	3	4	4,25	5,25	6,25	7,25	8,25
ρ , кг/м3,	ρ 1	ρ2	ρ 3	ρ 4	ρ 5	ρ6	с 1	с 2
c i	11600	6600	19200	10200	3920	3920	965,5	0,0735
	ε 1	ε2	ε s	ε 3	^^^^~ sA	^^^^~ s 1	^^^^~ s 2	^^^^~ sk
ε i , si	0,203	0,302	0,25	0,31	1,484	1,584	1,984	2,084
Δ i , δ , Вт/(м2 ⋅ К);	Δ 1	T 1* , К	T 2* , К	δ	Δ 2	RN , м	d , м	Lk , м
T 1* , T 2* , d , RN , Lk	1 000	1 800	700	10 000	200	0,1	2,5 ⋅ 10–4	0,04

Из уравнений (27) следует, что в любом сечении электродов, перпендикулярном оси s , выполняется соотношение

I ₁( s ) + I ₂( s ) = I_R , где I ₁( s ) = 2 π R ₁ ∫ ^s ₁ J ( T _2,4, T _1,3, Δ V ) ds — сила тока, текущего по эмиттеру; I_R — сила тока внешней цепи;

I2(s) = 2πR1∫2 J(T2,4, T1,3, ΔV)ds — сила тока, s текущего по коллектору, которая находилась по методике, описанной в работе [14].

Комбинируя уравнения (26) и (27), запишем, как в работе [12], дифференциальное уравнение для разности потенциалов между электродами ЭГЭ

d

T ^v = ds

R         ^s 2

8 ₄( R - 8 ₄/2) ^J^ ² J^²⁴’ ^Г1 - ³’ ^AI^ ^ds ^-

^R i 8 з ( Л i + 8 3 /2)

s

J ^ J(T24- 713- A^0 ds - s i                       ’            ’

которое определяет условия генерации плотности тока МЭЗ в каждой точке по координате s . Если потенциал эмиттера в точке s = s ₁ принимаем равным V ₁( s = s ₁) = 0, то потенциал коллектора в этой точке будет равным сумме падений напряжений на эмиттере, коммутационных деталях электродов и нагрузки:

V 2 ( s = s 1 ) = V 1 ( s = s 2 ) + U E _c + U R + U C _c .

Тогда начальное условие для уравнения (27) запишется в виде

s

i

A V ⁽ s = s 1 ) = ^ R -T^y I ^ 1 ^{( T 24} T 1,3 ’ ^A V ) d^{s +}

(2n S,K        2n s 1     A

^{+ Z} R [ "V * ^ 1 D ^{S +} < J ^ 2 ^Ds I ^{+ U} R -

V Э i s 2           3 2 0/

В отличие от источника [12], в данной работе рассмотрен общий случай: коллектор не эквипотенциален, и электропроводность электродов и коммутационных деталей зависит от их температуры. Самосогласованное решение уравнений (28), (29) для распределенных температурных полей, полученных из уравнений (1)–(25), определяет рабочую точку на характеристике ЭГЭ.

Результаты численного решения и их анализ

На рис. 2 показаны зависимости электрического тока от времени — кривые 1 и 2 для U_R = 0,06 В = const (сплошные кривые) и R _H = 2,0∙10^–4 Ом = const (штриховые кривые). Цифрой 1 обозначены результаты, полученные для случая, когда охлаждающим (шестым) слоем ТЭТЗ является воздух; 2 — охлаждающий слой He.

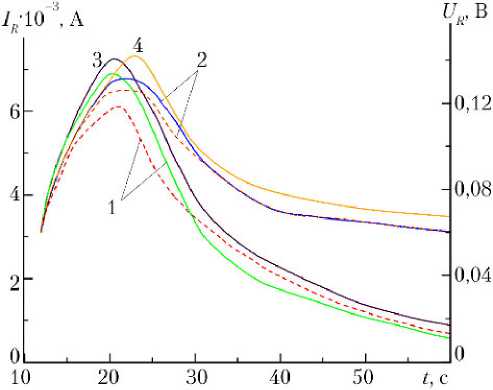
Рис. 2. Зависимость от времени значений электрического тока и выходного напряжения ЭГЭ ТЭТЗ: 1 — опорный режим прогрева, когда охлаждающим шестым слоем является воздух; 2 — теплоноситель гелий в шестом слое составной оболочки; 3 — зависимость от времени напряжения на нагрузке (ЭГЭ) U_R при охлаждении воздухом; 4 — охлаждение He. Сплошные кривые 1, 2 — для U_R = 0,06 В = const; штриховые кривые — R_H = 2,0∙10^–4 Ом = const

Из рис. 2 видно, что соответствующие сплошные и штриховые кривые близки как по значениям, так и по форме для большинства значений времени из моделируемого интервала. Заметные отличия силы тока I_R имеются в области их максимальных значений ( t ≈ 20 c). Для кривых 1 отличие составляет 10%, для кривых 2 — 4%. Причем бóльшие значения силы тока наблюдаются для первого типа характеристик ( U_R = const, сплошные кривые). Заметно отличаются между собой сплошные кривые 1 и 2 в области t > 30 с. Например, для t = 60 c отношение силы токов максимально и приблизительно равно 5.

Интерес представляет анализ диапазона изменения напряжения U_R для второго типа характеристик ( R _H = const). Кривые 3 (охлаждение воздухом) и 4 (охлаждение He) рис. 2 показывают изменения напряжения нагрузки (ЭГЭ) U_R . Обе кривые имеют максимумы ( U_R ≈ 0,15 В) в области t ≈ 20 c, но кривая 4 (охлаждение He)

спадает более медленно, т. е. значительное напряжение на нагрузке ( U_R ≈ 0,07 В) сохраняется в большем диапазоне времени. Таким образом, при охлаждении He ТЭТЗ сохраняет свою эффективность вплоть до t = 60 c. В свою очередь, для первого типа характеристик ( U_R ≈ 0,06 В = const) при вариации времени t в диапазоне 12…60 c изменение сопротивления нагрузки составляет 2,0∙10^–5…1,0∙10^–4 Ом.

На рис. 3, 4 приведены зависимости внешней температуры поверхности тела T_w и эмиттера T_L вдоль оболочки по s .

Сплошные кр³ивые 1–5 на рис. 3, 4 соответствуют моментам времени t : 1 — 20 с; 2 — 25 с; 3 — 30 с; 4 — 40 с; 5 — t = t_z ( t_z = 60 с соответствует стационарному режиму процесса нагрева тела) и получены для опорного режима прогрева, когда в шестом слое составной оболочки (см. рис. 1) в качестве теплоносителя используется воздух. На рис. 3, 4 штриховые кривые соответствуют варианту отсутствия термоэмиссионного охлаждения (ТЭО) эмиттера в те же самые моменты времени. Как видно из рис. 3, 4, наличие ТЭО снижает максимальную температуру поверхности оболочки T_w на 170 К при t = 30 с, а температура поверхности эмиттера уменьшается на некоторых участках траектории на 166–223 К. Уменьшение температуры внешней оболочки, связанное с электронным охлаждением эмиттера, качественно согласуется с данными работы [9].

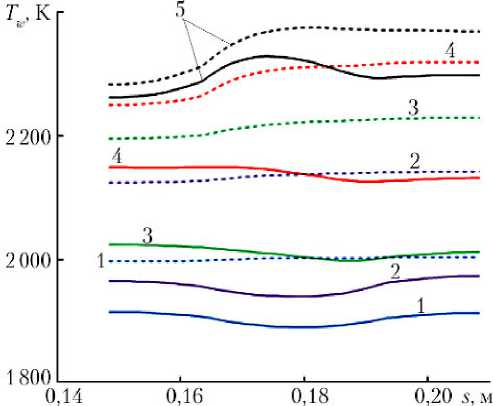
Рис. 3. Зависимость внешней температуры поверхности тела от продольной координаты для опорного режима теплообмена в различные моменты времени t: 1 — 20 с;

2 — 25 c; 3 — 30 c; 4 — 40 c; 5 — t = tz

Примечание. Сплошные кривые соответствуют наличию термоэмиссионного охлаждения, штриховые — его отсутствию.

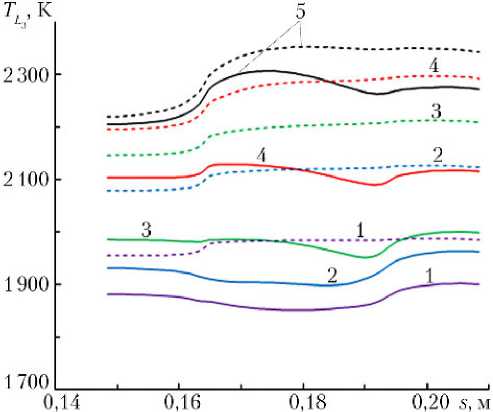
Рис. 4. Зависимость температуры поверхности эмиттера от продольной координаты для опорного режима прогрева Примечание. Обозначения такие же, как на рис. 3.

Если в качестве теплоносителя в шестом слое взять гелий с начальной температурой T ₂( δ ₆) = 200 К, теплофизические характеристики которого известны [19], то максимальная температура поверхности коллектора (рис. 5, штриховые кривые) не превышает T_{L 4} = 1 522 К, а эмиттера — T_{L 3} = 2 140 К при t = t_z . Как известно [1], теплоноситель с меньшей молекулярной массой оказывается более эффективным с точки зрения тепловой защиты.

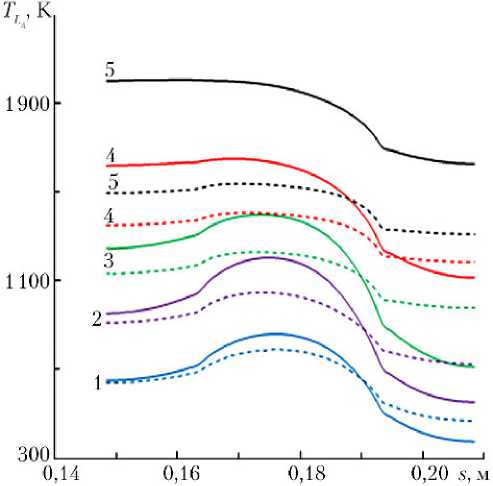
Рис. 5. Зависимость температуры поверхности коллектора от продольной координаты в те же моменты времени, что и на рис. 3

Примечание. Сплошные кривые соответствуют опорному режиму прогрева, штриховые — теплоносителю гелию в шестом слое составной оболочки.

Для практики представляет интерес величина температуры внутренней стенки T_{L 8} конструкции для коллектора. На рис. 6 сплошные кривые соответствуют распределению температуры по глубине n в центре тела ( s _* = ( L_k – s_A )/2) для опорного режима прогрева, штриховые — теплоносителю гелию в те же самые моменты времени. Оказалось, что температура внутренней стенки подложки увеличилась незначительно в момент t = t_z до T_{L 8} = 288 К.

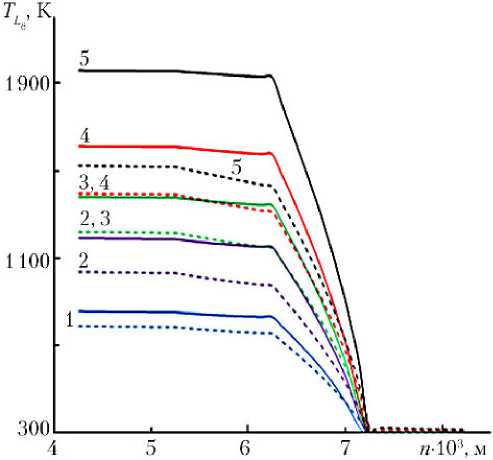
Рис. 6. Зависимость температуры коллектора по глубине n в центре тела s* в те же моменты времени, что и на рис. 3

Примечание. Обозначения такие же, как на рис. 4.

Отметим также, что в области больших величин плотности эмиссионного тока J (рис. 7) распределения внешней тем- пературы поверхности T , эмиттера T w L3

имеют вогнутость (см. сплошные кривые 1–3 на рис. 3, 4), а распределение температуры поверхности коллектора TL4 — выпуклость (см. рис. 5) в области действия ТЭО, при этом максималь- ная температура коллектора достигает TL4 = 1 992 К для t = tz.

На рис. 7 даны распределения плотности эмиссионного тока J (сплошные кривые) и силы тока I ₁ (штриховые кривые), текущего по эмиттеру в области 3 , для воздушного теплоносителя в шестом слое (см. рис. 1) вдоль координаты s в те же самые моменты времени.

Из сравнения рис. 4 и 7 видно, что наибольший эффект охлаждения эмиттера на траектории отвечает максимальным значениям J и I ₁ при t = 25–30 с.

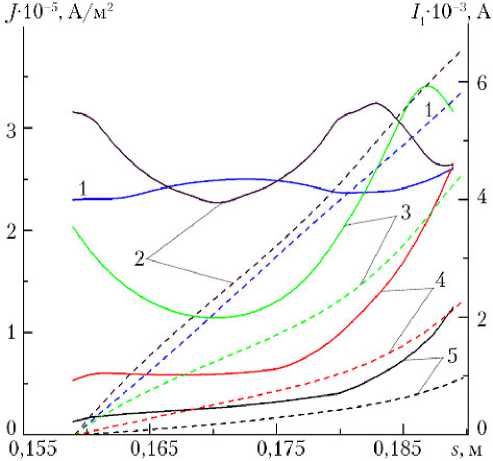
Рис. 7. Зависимость распределения плотности тока эмиссии (сплошные кривые) и силы тока (штриховые кривые) в области 3 (см. рис. 1) от продольной координаты для опорного режима прогрева в те же моменты времени, что и на рис. 3

Заключение

Разработана математическая модель возможного варианта исполнения термоэмиссионной тепловой защиты теплонапряженных элементов ВЛА при аэродинамическом нагреве в воздушной атмосфере за счет «внутреннего» электронного охлаждения многослойной оболочки летательных аппаратов при ее конвективном нагреве в приближении турбулентного режима течения в пограничном слое химически равновесного воздуха; установлен соответствующий эффект снижения температуры эмиттера ЭГЭ/оболочки ВЛА на 170–223 К, качественно согласующийся с известными данными в исследуемой предметной области; качественное согласие результатов расчета, по-видимому, связано с принятыми в работе упрощениями и исходными данными.