Моделирование тонких структур в распределениях продуктов ядерных реакций по массе и их распознавание методами машинного обучения

Теоретические описания ядерных реакций, таких как деление и квази-деление, позволяют представить эволюцию ядерной системы в виде траектории в многомерном деформационном пространстве. Выявление образов таких траекторий в пространстве экспериментально наблюдаемых переменных было предложено в работах [1-4] в качестве нового подхода к анализу данных. Обсуждаемые траектории выглядят как «тонкие структуры» в двумерных распределениях, например, в корреляционных массовых распределениях. По определению, термин «тонкая структура» означает локальные области (пики) двумерного распределения с выходом выше, чем на гладкой подложке, являющейся фоном для искомого эффекта. Для выявления тонких структур с заданным уровнем достоверности в работе [5] применялись методы морфологического анализа изображений.

Иногда условия эксперимента позволяют наблюдать траекторию, связанную с эволюцией ядер-ной системы, почти без шума (фона). Траектория в этом случае выглядит как непрерывная последовательность точек, например прямая, в двумерном распределении экспериментально наблюдаемых переменных. В работе [6] преобразование Хафа [7] было применено как для выявления линейной структуры, так и для оценки уровня ее достоверности по отношению к альтернативной гипотезе о том, что фактически наблюдается только случайная последовательность точек.

В данной работе предлагается решение аналогичной задачи, но для гораздо более сложной структуры. Корреляционные массовые распределения осколков деления из спонтанного деления калифорния ²⁵²Cf(sf)¹ представлены на рис.1. Мы отсылаем читателей к работе [8], где представлены экспериментальные детали.

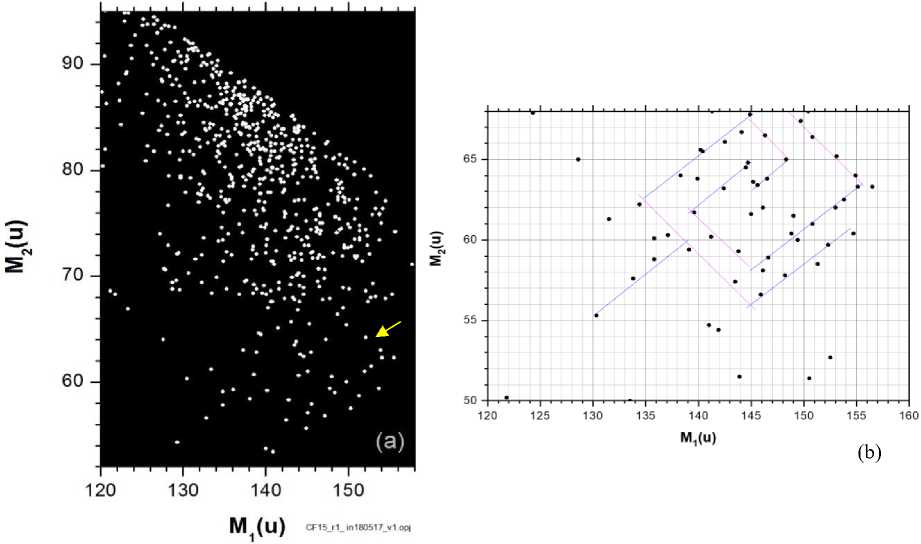
Рис. 1. Корреляционные массовые распределения осколков деления из 252Cf (sf) – (a). Специфическая ромбо-спиральная структура в нижней части рисунка («ядерная роза») отмечена стрелкой. Эта же структура в более крупном масштабе (b) [8].

Ромбо-спиральная структура (ромбический меандр) в правом нижнем углу рис. 1 (а) - изображение, напоминающее розу - было названо «ядерной розой». Он состоит из семейства линий М 1 + М₂ « const и нескольких линий, почти перпендикулярных им. Трактовка первого семейства линий представлена в [8], в то время как второе семейство еще нуждается в физической интерпретации.

Метод поворотных гистограмм

Так как моделируемая тонкая структура состоит из прямых линий, проходящих через скопление некоторых точек, первоначальным подходом для построения модели ромбического меандра было выбрано преобразования Хафа [7]. Преобразование Хафа - это вычислительный алгоритм, применяемый для параметрической идентификации геометрических элементов растрового изображения и состоящий в переходе из пространства измерений в пространство параметров (рис. 2).

Рис. 2. Преобразование Хафа

Параметризация вида х cos9 + у sinQ = р , более сложная, чем в обычном уравнении прямой линии вида у = ах + Ь, была предложена П. Хафом, чтобы избежать случаев обращения в бесконечность параметра а в обычном уравнении прямой при ее приближении к вертикали. Однако, в случае с моделированием ромбического меандра ориентация всех отрезков прямых близка к ±45° , поэтому был использован метод поворотных гистограмм, предложенный в [9], как более простой и быстрый вариант преобразования Хафа, для обнаружения прямых линий

Идея метода состоит в фрагментации исследуемого региона на узкие параллельные полосы, в каждой из которых подсчитывается количество попаданий. Угол а наклона полос постепенно изменяется от с_т ; _п до сс_тах. Когда одна из таких полос совпадает с каким-либо прямолинейным отрезком, в гистограмме, соответствующей данному наклону полосы, возникает максимум. Для заполнения столбцов гистограммы используется метод проекций. Точки проецируются на ось Y под фиксированным углом оп правилу Y_pr = у — х tga. Критерием обнаружения линии, является условие, что значение соответствующего столбца гистограммы должно превысить заданный порог (рис. 3).

Граница коридора в методе поворотных гистограмм может разрезать прямую пополам так, что ее половинки попадут в соседние коридоры и число точек в обеих половинках не превысят порог так, что линия не будет найдена. Решить эту проблему можно одним из следующих способов:

• -    вычислять направление линии как центр тяжести трех полос;

• -    увеличить ширину полос гистограммы на небольшую величину так, чтобы полосы немного пересекались.

Для устранения возникающих дубликатов во втором способе необходимо запоминать точки, принадлежащие одной прямой и отбрасывать их из других, при повторном фиксировании точки в другой линии.

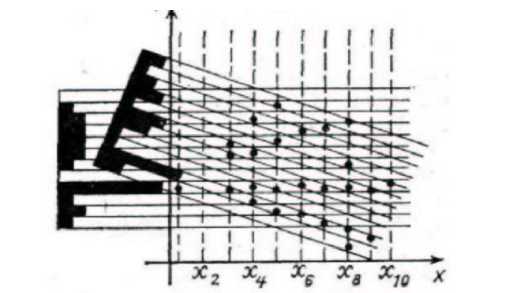
Рис. 3. Графический пример принципа работы метода поворотных гистограмм

Для определения параметров найденных прямых и разброса точек вокруг них, использовалась подгонка методом наименьших квадратов (см. например, [10]). Суть метода состоит в подборе такой функции у = /(х), график которой проходит как можно ближе к точкам. Функция должна быть достаточно проста, в нашем случае точки выстраиваются в линию, следовательно, уравнение прямой у = Лх + В подходит лучше всего для решения задачи. В итоге, все сводится к нахождению коэффициентов Л и В, чтобы сумма квадратов отклонений 5 = ЕП=1(У; — (Лх; + В))2 была минимальной. Для нахождения коэффициентов Л и В дифференцируют функцию 5 по этим параметрам и решают полученную систему уравнений. Важной характеристикой такой подгонки является значение а среднеквад ратичного разброса точек вокруг найденной прямой а =

I⁵min /

И

—

2 .

Получение характеристик ромбического меандра

Применение метода поворотных гистограмм с последующей МНК подгонкой найденных прямых оказалось весьма существенным этапом моделирования ромбического меандра, поскольку вначале на его исходном изображении не были известны точно, как направления предполагаемых отрезков прямых, так и положения угловых точек, определяющих длины этих отрезков. То, что наблюдатель мог разглядеть на изображении и вручную выделить какие-то точки, близкие к неким отрезкам, было слишком произвольным и зависело от искусства наблюдателя. Потребовались независимые от наблюдателя объективные инструменты поиска отрезков с неизвестным заранее направлением с последующей подгонкой прямых для определения точного угла их наклона, величины разброса точек вокруг отрезков, всех точек пересечения найденных отрезков и распределения числа точек на каждом из отрезков. Такими инструментами и явились методы Хафа, МНК подгонки и статистической обработки полученных множеств точек.

Таким образом, было установлено, что ромбический меандр состоит трёх простых линейных структур:

• -    линии параллельные осям масс;

• -    линии М 1 + М 2 константа - 45° по оси М 1 ;

• -    линии М 1 — М 2 константа - 135° по оси М 1 .

На пересечениях прямых находятся точки, координаты которых близки к массам известных магических ядер [11].

В результате статистического анализа распределения точек по отрезкам прямых, образующих меандр, было установлено, что точки распределены по отрезкам равномерно, а их количество на каждом из отрезков имеет распределение Пуассона с параметром Л. В предположении, что этот параметр является общим для всех отрезков меандра, он был оценен по критерию Колмогорова, как Л = 4.5. В предположении, что разброс точек вокруг отрезков одинаков для всех отрезков подчинен нормальному закону с параметрами (0, ст) параметр ст был также оценен по критерию %2 , как ст = 0.2.

Для оценки надежности тонкой структуры относительно альтернативной гипотезы о том, что эта структура является набором случайно рассеянных точек, было принято решение использовать нейросетевой классификатор и таким образом решить задачу классификации изображений. Для решения задачи необходимо было:

• -    создать числовую модель тонкой структуры;

• -    создать генератор изображений и сгенерировать изображения двух различных типов:

о изображения с тонкой структурой;

о изображения со случайным разбросом точек по тому же полю;

• -    создать модель искусственной сверточной нейронной сети (ИСНС);

• -    обучить и протестировать ИСНС как классификатор.

Моделирование ромбического меандра

После получения всех характеристик каждой прямой ромбического меандра, появилась возможность смоделировать неограниченное число изображений для создания набора данных, требуемых для тренировки и тестирования ИСНС. Была разработана программа - генератор изображений «розы» с использованием языка программирования Python . Программа работает следующим образом: вначале в соответствии с заданными параметрами на поле ромбического меандра откладываются 6 горизонтальных и 4 вертикальных отрезков, количество точек на каждом из отрезков разыгрывается по распределению Пуассона с параметром Л = 4.5, а сами точки разбрасываются случайно вдоль отрезков. Далее точки размазываются под прямым углом к отложенным отрезкам, в соответствии с нормальным законом с параметрами (0, ст) , где ст = 0.2, после чего вся структура поворачивается под углом 45° к оси абсцисс, превращаясь в цифровую модель ромбического меандра.

Генератор создает изображения двух классов, на первом - модель этой тонкой структуры, сгенерированная по вышеуказанному алгоритму (см. пример на рис. 4), на втором - равномерно рассеянные точки по тому же полю в количестве, совпадающем с числом точек, образующем соответствующий меандр (рис. 5).

Перед составлением тренировочного набора, изображения приводятся к одному виду: все картинки должны быть одного размера (80х80 пикселей), с одинаковыми точками, вместо их цвета и размера, подписей и линий осей изображения снабжаются метками принадлежности к тому или иному классу. Для обучения и тестирования нейроклассификатора было создано 15 тыс. изображений обоих классов, которые были разделены в следующей пропорции: 20 тыс. для обучения модели сети и 10 тыс.

для тестирования (в обоих наборах количество изображений каждого из классов одинаково, а сами изображения тщательно перемешаны).

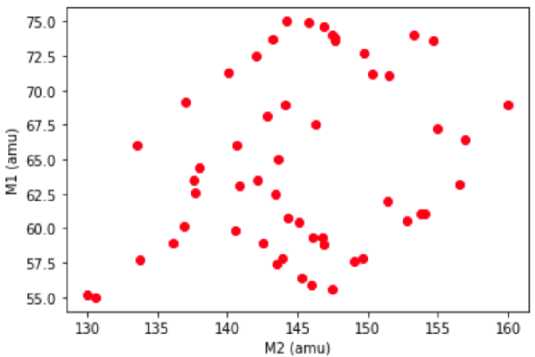
Рис. 4. Пример – сенерированная реализация ромбического меандра

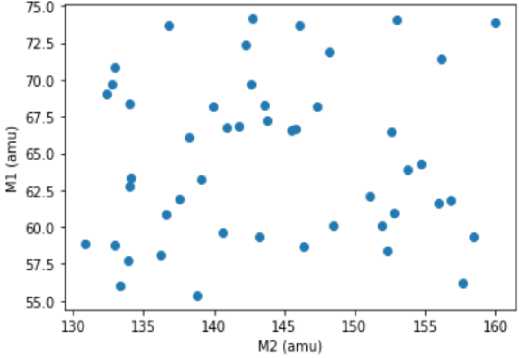
Рис. 5. Пример – альтернативного изображения из точек, равномерно распределенных по полю меандра

Искусственная сверточная нейронная сеть

Для решения задачи классификации с учителем можно использовать два типа искусственных нейронных сетей:

• -    многослойный персептрон;

• -    сверточные нейронные сети.

Авторами статьи была выбрана сверточная нейронная сеть, так как персептрон не приспособлен для ввода двумерных изображений, которые приходится предварительно разворачивать в одномерный вектор, теряя при этом существенную информацию о связях соседних пикселей изображения. Кроме того, в персептроне каждый нейрон связан со всеми нейронами предыдущего слоя, причём каждая связь имеет свой персональный весовой коэффициент, в то время как в сверточной нейронной сети применяются операции свёртки (рис. 6), где используется лишь ограниченная матрица весов небольшого размера, которую «двигают» по всему обрабатываемому слою, формируя после каждого сдвига сигнал активации для нейрона следующего слоя с аналогичной позицией. Таким образом, для различных нейронов выходного слоя используются одна и та же матрица весов. В этом подходе следующий слой, получившийся в результате операции свёртки такой матрицей весов, показывает наличие данного признака в обрабатываемом слое и её координаты, формируя карту признаков. Операция пу-линга (рис. 7) позволяет выделить важные особенности на картах признаков, а также снижает размерность карт, ускоряя время работы сети.

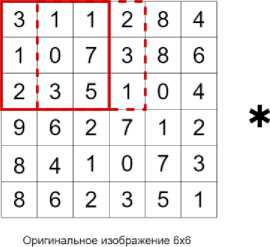
Рис. 6. Пример выполнения операция свертки

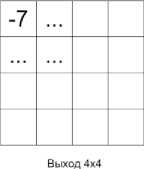
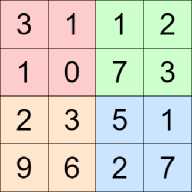
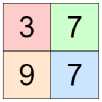
Рис. 7. Пример выполнения операции макспулинга

фильтр 2x2 с шагом 2 и функцией max

В качестве функции активации для слоев свертки использовалась функция ReLU (1), которая является одной из самых распространенных в ИСНС:

f(x) = max(0, x).

После слоев свертки и пулинга получается множество карт признаков. Их соединяют в один вектор и этот вектор подают на вход полносвязному слою нейронов. Выход полносвязного слоя подается на вход одному единственному нейрону с сигмоидальной функцией активации (2), которая группирует к центру крайние слишком большие входные значения, что позволяет находить четкие границы при предсказании.

f(x) =

1 + е-Лх.

Минимизация функции потерь нейросети оценивает качество работы всей модели. В нашем случае использовалась бинарная перекрёстная энтропия [13] вида (3):

N

Hp(q) =-^^[yi *log (p(yi)) +(1 - yi) * log(1-p(yi))],           (3)

где у - метка (равная 1 для изображений с ромбическим меандром и 0 для изображений со случайно рассеянными точками), а р(уЦ - прогнозируемая вероятность того, что на изображении присутствует ромбический меандр во всех N случаях.

Была использована следующая модель нейронной сети, после каждой второй свертки происходила операция макспулинга (рис. 8):

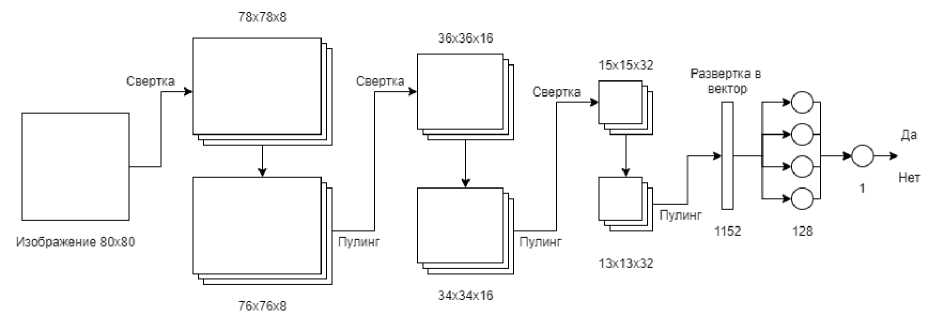
Рис. 8. Модель сверточной нейронной сети

Результаты обучения и тестирования нейроклассификатора

В процессе обучения данной модели для минимизации функции потерь ИСНС использовался оптимизатор ADAM [14], т.к. он сочетает в себе и идею накопления движения и идею более слабого обновления весов для типичных признаков. Скоростью обучения бралась равной 0.0001. Размер батча составил 256 изображений. Все это способствовало плавному обучению сети, не допуская ее переобучения. После 25 эпох обучения на 20 тыс. сгенерированных изображений обоих классов, модель сверточной нейронной распознала правильно 99% экземпляров из тестовой выборки. 1% ложных предсказаний могут указывать на ошибки генератора ромбического меандра. Графики обучения представлены на рисунке 9.

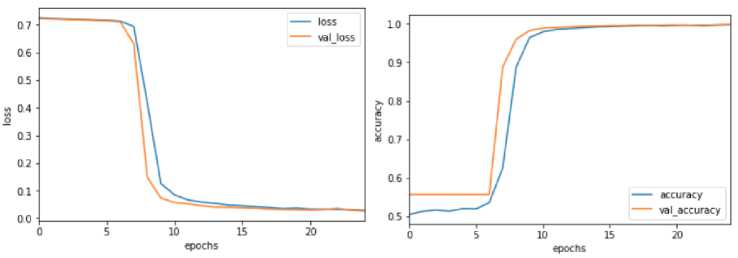
Рис. 9. Изменение ошибки на тренировочной ^(a) овой выборке (a). Изменение точност ^(b) зна-вания на тренировочной и тестовой выборке (b)

Из графика видно, что 99% точность идентификации тонкой структуры была достигнута к 15 эпохе, однако обучение нейроклассификатора на этом не закончилось, поскольку, как видно на графике (рис. 10) прослеживается медленное, но постепенное улучшение качества распознавания.

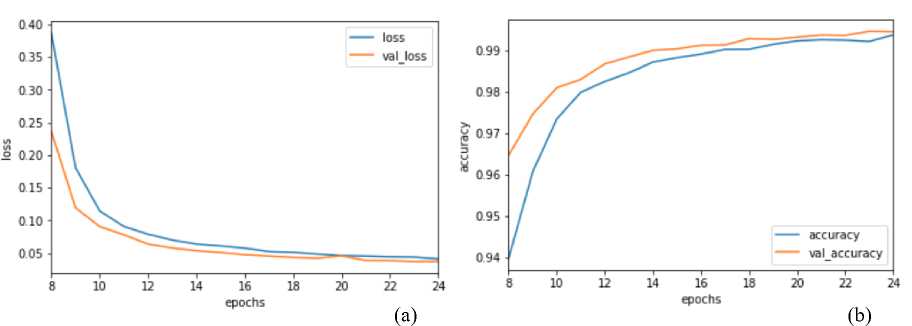
Рис. 10. Изменение ошибки на тренировочной и тестовой выборке (a). Изменение точности распознавания на тренировочной и тестовой выборке (b)

Так как важным считается не допустить переобучение ИСНС, обучение было остановлено на 25 эпохе, чтобы в результате чрезмерной подгонки параметров модели к зависимостям в обучающем множестве, модель не потеряла возможность распространять обнаруженные закономерности на новые данные. Из рисунка 10 видно, что модель сохраняет способность к обобщению, так как оранжевая линия (точность распознавания изображений тестовой выборки) находится выше синей (точность распознавания изображений обучающей выборки).

После всех проведенных работ пришло время ответить на главный вопрос. Является ли «ядерная роза» случайной последовательностью рассеянных точек? Обработанное изображение (рис. 1 (b)) было подано на вход ИСНС. На выходе модель сети выдала вероятность нахождения на картинке ромбического меандра с вероятностью 99.913955%, что говорит о правильности примененных методов по выявлению характеристик тонкой структуры, по проведению моделирования и обучения нейроклассификатора.

Кроме того, физики попросили нас вычислить вероятность события, когда случайная комбинация точек будет принята за ромбический меандр. Расчет был выполнен по следующей схеме. После предъявления шумового изображения на вход обученного бинарного нейроклассификатора бралась максимальная из двух, выдаваемым им вероятностей Р_тах. Если она соответствовала классу «роза», то проверялось превышение порога Т = 80% подходящего для разумной классификации. Таким образом, если проверка выполнялась п раз и в т из них получалось Р_тах > Т, то искомая вероятность Р = т/п.

При расчете на п = 100 тыс. изображений из случайно рассеянных точек по полю ромбического меандра, получилось т = 66, т.е. Р = 0.00066.

Заключение

Рассмотрены различные методы машинного обучения для построения числовых моделей проявлений кластеризации в редких многотельных распадах тяжелых ядер на примере исследования спонтанного деления калифорния. На основе статистического анализа реализована числовая модель тонкой структуры и разработана программа-генератор как тонкой структуры, так и её альтернативной стоха-стичекой модели. Построена и обучена модель искусственной сверточной нейронной сети, для решения задачи классификации. Полученные результаты тестирования нейроклассификатора доказывают статистическую обусловленность и достоверность предложенной модели тонкой структуры в виде ромбического меандра в корреляционных массовых распределениях ядерных реакций калифорния ²⁵²Cf(sf) . Проведенные исследования показали эффективность использования искусственных нейронных сетей в исследуемой физической проблеме.